基于PSO-BP神經網絡預測廣州市日均PM10濃度*

南方醫科大學公共衛生學院生物統計學系（510515） 尹安琪 林愿儀 林偉俊 歐春泉

基于PSO-BP神經網絡預測廣州市日均PM10濃度*

南方醫科大學公共衛生學院生物統計學系（510515） 尹安琪 林愿儀 林偉俊 歐春泉△

目的應用多元線性回歸模型和PSO-BP神經網絡模型對廣州市日均PM10濃度進行提前一天的預測，比較兩種模型的預測效果，為環境管理決策提供依據。方法利用廣州市2008年1月1日至2011年11月30日的PM10濃度和氣象資料分別構建兩種模型，并使用2011年12月1日至12月31日的數據檢驗兩模型的預測效果。結果前一天的PM10、極大風速、最小相對濕度、日平均氣溫、能見度為預測第二天PM10濃度的5個主要影響因素，其中前一天的PM10濃度與預測的PM10濃度相關性最高（0．66）。PSO-BP神經網絡模型的決定系數（R2）為0．80，相比于多元線性回歸模型，其均方根誤差（RMSE）降低6．20%，平均絕對誤差（MAE）降低8．73%，平均絕對百分比誤差（MAPE）降低13．33%，平均絕對偏差百分比（PMAD）降低8．67%。結論PSO-BP神經網絡模型預測效果優于多元線性回歸模型，能有效模擬、預測未來一日的PM10濃度，可為大氣顆粒物濃度預測提供一定的方法學參考。

多元線性回歸 PSO-BP神經網絡 PM10氣象因素 預測

世界衛生組織最新估計數據顯示：每年有700萬例的過早死亡與大氣污染有關。大氣中懸浮顆粒物（particulate matter，PM）濃度的升高可導致人體肺功能的降低以及心肺疾病發病和死亡風險的上升［1－3］。直徑小于或等于10μm的顆粒物（PM10）是影響人群健康的主要顆粒污染物。及時、準確地預測PM10濃度，有利于大眾采取積極的應對措施以降低對健康的影響。目前，國內許多學者開始研究城市大氣污染物濃度預測模型。吳嘉榮［4］通過建立線性回歸模型對福建泉州的PM10濃度進行了簡單預測，但未進行預測效果評價。李祚泳等［5］率先將神經網絡應用于大氣污染預測的探索性研究，預測了SO2的濃度，并指出BP網絡的預測精度優于模糊識別模型的預測精度。石靈芝等［6］基于BP人工神經網絡對長沙市PM10每小時濃度進行預測，但預測時間較短（2008年1月5日至2008年1月9日，共五天），整體R2為0．62。國內現有文獻普遍采用當天的氣象數據預測當天的PM10濃度，而當天的氣象數據作為預報指標本身也存在準確性的問題，勢必影響PM10濃度的預測效果；其次，不同模型的預測效果尚有待比較，尤其是復雜的神經網絡方法是否優于傳統的多元線性模型有必要予以探討。

廣州市作為珠江三角洲重點經濟發展城市，尚未深入開展有關顆粒物預測的研究。本研究基于廣州市2008年1月1日至2011年11月30日PM10濃度和氣象數據，建立傳統的多元線性回歸模型以及PSO-BP神經網絡模型預測PM10濃度，并對兩模型預測效果進行比較，可為環境管理決策提供依據，同時也可為其他地區的同類研究提供方法學上的借鑒。

資料與方法

1．資料來源

從廣州市環境保護局官網獲得2008－2011年廣州市9個監測站點的日均PM10濃度數據。從中國氣象科學數據共享服務網獲得廣州市2008年－2011年氣象因素數據；從Weather Underground網站獲得2008－2011年能見度數據。

2．方法原理

經過逐步回歸方法篩選出與預測日期相對應的前一天氣象因素等變量：PM10（PM10t-1）、極大風速（JDFSt-1）、最小相對濕度（M inRHt-1）、日平均氣溫（Tempt-1）、能見度（Seet-1）等5個主要預測變量來預測當日PM10（PM10t）濃度。利用2008年1月1日至2011年11月30日的PM10濃度和氣象資料分別構建以下兩種模型，并用2011年12月1日至12月31日的數據檢驗兩模型的預測效果。

（1）多元線性回歸模型

多元線性回歸模型是探討一個變量和多個變量之間關系的常用方法，主要以多個自變量的最優組合共同預測或估計因變量，其在環境大氣污染研究中也常被使用。多元線性回歸模型的主要形式如下：

其中，Y是因變量（預測變量），β0是常數，β1，β2，…，βp是自變量X1，X2……Xp的回歸系數，ε是殘差（觀測值與預測值的差值）。回歸系數β0，β1，β2，…，βp常用最小二乘法求得［7－8］。

（2）PSO-BP神經網絡模型

BP神經網絡屬于多層感知器（multi-layer perceptions，MLP）的一種，能夠解決預測中的線性不可分問題。多層感知器除了輸入層和輸出層外，還具有若干隱含層。上下層之間實現全連接，而每層單元之間無連接。大部分情況下多層感知器采用誤差反向傳播（back propagation）的算法進行權值調整，即當一學習樣本提供給網絡之后，神經元的激活值從輸入層經中間層向輸出層傳播，在輸出層的各個神經元獲得網絡的輸入響應。隨后，按照減小目標輸出與實際誤差的方向，從輸出層經過中間層逐層修正各層的連接權值，最后回到輸入層。

粒子群優化算法（PSO）是一種實現簡單、全局搜索能力強且性能優越的啟發式搜索技術。在PSO算法中，每個粒子都代表極值優化問題的一個潛在最優解，用位置、速度和適應度值三項指標表示該粒子的特征，適應度值由適應度函數計算得到，其值的好壞表示粒子的優劣。粒子在解空間中運動，通過跟蹤個體極值Pbest和群體極值Gbest更新個體位置，個體極值Pbest是指個體所經歷位置中計算得到的適應度值最優位置，群體極值是指種群中的所有粒子搜索到的適應度最優位置。粒子每更新一次位置，就計算一次適應度值，并且通過比較新粒子的適應度值和個體極值、群體極值的適應度值更新個體極值Pbest和群體極值Gbest。

PSO-BP神經網絡模型可優化BP神經網絡的權值和閾值，避免BP神經網絡陷入局部極小值和增加其泛化性能，提高預測精度。PSO的適應度函數為神經網絡的輸出誤差，公式為：

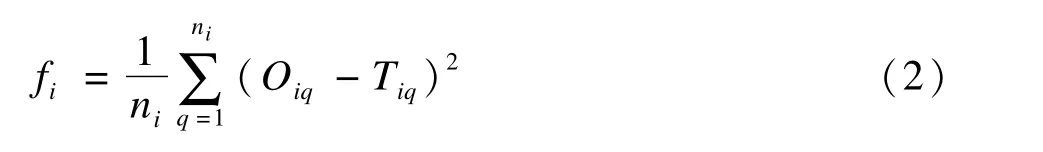
其中，ni為訓練樣本的個數，Oiq、Tiq分別為訓練樣本q在第i粒子的位置所確定的網絡權值和閾值下的網絡實際輸出和期望輸出［9］。

PSO-BP神經網絡算法的具體步驟為：

①初始化BP神經網絡和粒子群

根據樣本數據設計BP網絡的輸入、輸出和隱含層神經元數目、學習函數及訓練函數；根據粒子群的規模，按照個體結構產生一定數目的粒子群，其中不同的個體代表神經網絡的1組不同的權值。同時，初始化粒子的速度、位置、個體歷史最優pi、全局最優pg、迭代誤差精度和最大迭代次數等［10］。

②迭代與更新

更新粒子的速度和位置，并計算粒子的適應值。判斷當前迭代次數是否大于最大迭代次數或當前最優適應值是否小于設定精度，若滿足條件，則輸出全局最優粒子位置及BP網絡的權值和閾值。

③訓練BP網絡

根據輸出的BP網絡權值和閾值訓練BP神經網絡，并運用測試樣本進行檢驗，PSO-BP神經網絡完成。

（3）模型評價指標

采用以下指標評價模型的預測準確性：均方根誤（RMSE），平均絕對誤差（MAE），平均絕對百分比誤差（即相對誤差，MAPE），平均絕對偏差百分比（PMAD）和決定系數（R2）［11］。

（4）數據預處理

2008－2011年，日均PM10數據有17個缺失值（占PM10數據的1．16%），能見度數據有12個缺失值（0．82%），對缺失數據采用線性插值方法填補，得到R2相差0．05以內，為保證時間序列的連續性，本文對缺失值進行填補。為了解極端值對模型的影響，本文將極端值定義為±3SD，其中，本研究PM10數據有22個極大值，12個均出現在冬季。廣州市屬于亞熱帶海洋性季風氣候，冬季來自北方大陸的冷風形成低溫、干燥、少雨的氣候，且冬季大氣層結穩定，較易出現逆溫，冬季氣候和逆溫層的出現會直接影響污染物的擴散，容易導致污染物濃度急劇上升。此外，冬季工業排放、汽車尾氣排放等產生的大氣顆粒物不能及時擴散，使PM10濃度大大增加，達到最大值。在剔除22個極端值后，模型R2僅降低0．01。為保留數據的原有特征，本文的最終分析并未剔除極端值。

（5）統計軟件

利用SPSS 20．0軟件構建多元線性回歸模型，利用Matlab 2014a軟件實現PSO-BP神經網絡模型的構建。

結 果

1．日均PM10濃度的季節性特征

2008年到2011年廣州市年均PM10濃度見圖1。四年間PM10濃度一直維持在70μg/m3左右的較高水平，2009年的PM10濃度的最大值甚至達到284．70 μg/m3。PM10濃度呈現冬春季高，夏秋季低的季節特征。

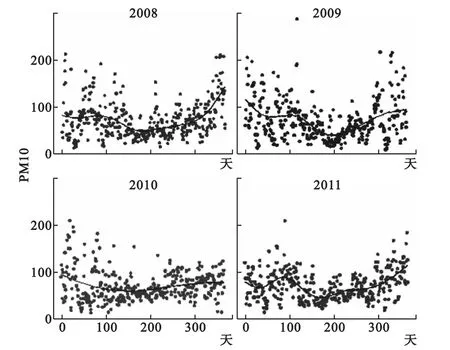
圖1 2008－2011年日均PM10濃度時序圖

2．模型的構建

（1）多元線性回歸模型

運用最小二乘法對多元線性回歸模型的參數進行估計，結果見表1。

表1 多元線性回歸模型參數估計值

表中可見各參數均有統計學意義，構建的PM10濃度預測的多元線性回歸模型為：

（2）PSO-BP神經網絡模型

根據所設定的參數，將相同的5個主要影響因素作為BP神經網絡的輸入層節點，對數據進行歸一化處理，相應地，對訓練后輸出數據進行反歸一化處理。通過訓練，最終構建了PSO-BP預測模型，并對31天（2011年12月）的日均PM10濃度進行預測。

3．兩個模型預測效果的評估和比較

兩個模型對2011年12月日均PM10濃度的預測值與實際觀測值的數據結果如表2所示。

表2 兩種模型的預測結果比較

根據表2我們對兩模型作圖比較（圖2）。

圖2 兩模型的預測值與觀測值比較

兩模型的預測效果的具體評價指標如表3所示，與多元線性回歸模型相比，PSO-BP神經網絡模型的RMSE、MAE、MAPE、PMAD均更小，決定系數更大。其中，PSO-BP神經網絡模型的平均絕對百分比誤差為16．9%，R2達到0．80，可認為此模型對廣州市日均PM10的預測效果較好，擬合效果與實際數據的誤差較小。由圖2可以看出，PSO-BP神經網絡對于波峰和波谷的擬合尤為精確。

表3 模型預測效果比較

討 論

近些年來，國內大氣顆粒物污染問題非常嚴峻，導致城市霧霾頻繁出現。目前，國內對于大氣質量預報范圍過大不夠精準，只將我國簡單劃分為京津冀、長三角、珠三角等區域，且大都僅限于用當天的氣象數據預測當天的顆粒物濃度，預測效果欠佳。

廣州市作為珠江三角洲重點經濟發展城市，按照WHO日均PM10濃度標準計算，廣州市2008年至2011年，PM10濃度超標率均大于60%，2009年日均PM10濃度最高甚至達到284．7μg/m3，超過WHO標準的四倍多。但目前廣州尚未深入開展有關顆粒物預測的研究。

本研究提出了構建BP算法和PSO算法結合的模型對廣州市日均PM10濃度進行提前一天的預測，發現PSO-BP神經網絡模型較普通多元線性回歸模型有更好的預測效果。多元線性回歸模型只能解決線性可分問題，而BP神經網絡模型能夠解決預測中的線性不可分問題，但其學習效率低、收斂速度慢，易陷入局部極小值，在應用中網絡結構的確定基本依賴經驗，主要是采用遞增或遞減的試探方法來確定網絡的隱節點，這些缺陷使得神經網絡的訓練樣本和測試樣本的輸出具有不一致性和不可預測性，極大地限制了神經網絡在實際預報中的應用［12］。本文將PSO優化算法與BP神經網絡相結合，是在BP網絡算法誤差反向傳播進行權值調整的基礎上，引入PSO算法對權值進行修正。此混合算法有效結合了兩者的優點，彌補了各自的不足。在基于PSO算法的BP網絡的權值修正過程中，BP網絡的權值作為PSO算法的粒子速度，根據適應度函數得到適應度值，根據適應度值找個體極值和群體極值，然后更新粒子速度和位置，輸出BP網絡的權值和閾值，從而達到訓練神經網絡的目的，此過程增加了模型的泛化性能，提高了預測精度。

本研究發現PM10濃度存在自相關，前一日的PM10濃度對預測當日的PM10濃度有較強的影響。前一日的氣象因素對于PM10有滯后影響，風速越大，越利于PM10的稀釋與擴散；濕度高，利于PM10凝結沉淀；溫度高，大氣對流作用強，利于PM10稀釋擴散；PM10濃度越高，能見度越低。本研究利用了氣象因素的滯后性和PM10濃度的自相關性，建立了適合廣州市的PM10預測模型，對日均PM10濃度實現了提前一天的預測。不過，由于廣州市監測站點有限，且均分布在廣州市中心城區，本文基于9個監測站點的數據僅能預測廣州市中心城區的日均PM10濃度。

［1］牟喆，彭麗，楊丹丹，等．上海市天氣和污染對兒童哮喘就診人次的影響．中國衛生統計，2014，31（5）：827-829．

［2］Gilmour PS，Brown DM，Lindsay TG，et al．Adverse health effects of PM10particles：involvement of iron in generation of hydroxyl radical．Occup Environ Med，1996，53（12）：817-822．

［3］Pope CR，Bates DV，Raizenne ME．Health effects of particulate air pollution：time for reassessment？Environ Health Perspect，1995，103（5）：472-480．

［4］吳嘉榮．用線性回歸法建立城市環境空氣質量預報模式．引進與咨詢，2005，12：29-30．

［5］曹蘭．空氣中PM_（10）濃度的BP神經網絡預報研究．環境研究與監測，2010，02：29-32．

［6］石靈芝，鄧啟紅，路蟬，等．基于BP人工神經網絡的大氣顆粒物PM lo質量濃度預測．中南大學學報，2012，43（5）：1969-1974．

［7］Ul-Saufie AZ．Comparison Between Multiple Linear Regression And Feed forward Back propagation Neural Network Models For Predicting PM10Concentration Level Based On Gaseous And Meteorological Parameters．International Journal of Applied Science and Technology，2011，1（4）：42-49．

［8］馬雁軍，楊洪斌，張云海．空氣污染預測與地面氣象要素應用．氣象科技，2004，32（2）：123-125．

［9］王愛萍，江麗．基于PSO的BP神經網絡學習算法．計算機工程，2012，38（21）：193-196．

［10］李慧民，李振雷，何榮軍，等．基于粒子群算法和BP神經網絡的沖擊危險性評估．采礦與安全工程學報，2014，31（2）：203-207．

［11］李驪，錢俊，楊軍，等．三種模型對廣東省傷寒副傷寒逐月發病數預測的比較．中國衛生統計，2014，31（2）：197-201．

［12］吳建生，劉麗萍，金龍．粒子群-神經網絡集成學習算法氣象預報建模研究．熱帶氣象學報，2008，24（6）：679-686．

（責任編輯：劉 壯）

Prediction of Daily Averaged PM10Concentrations Based on PSO-BP Neural Networks in Guangzhou

Yin Anqi，Lin Yuanyi，Lin Weijun，et al．
（Department of Biostatistics，School of Public Health，Southern Medical University（510515），Guangzhou）

ObjectiveTo apply Multiple Linear Regression model（MLR）and PSO-BP neural networks model to forecasting daily averaged PM10concentrations，and compare the performance of these two prediction models．MethodsBased on data of PM10concentrations and meteorology in Guangzhou from January 1，2008 to November 30，2011，we constructed the MLR model and PSO-BP neural networks model，and data from December 1 to December 31 in 2011 were used to assess the predictive validity of the models．ResultsThe previous day′s PM10，extreme wind speed，minimum relative humidity，daily averaged temperature and visibility were the main factors in forecasting PM10，particularly，the previous day′s PM10was strongly correlated with the forecasting PM10（0．66）．The determination coefficient（R2）of PSO-BPwas 0．80．Compared to MLR，PSOBP had a decrease of 6．20%in the root mean square error（RMSE），8．73%in the mean absolute error（MAE），13．33%in the mean absolute percenterror（MAPE）；and 8．67%in the percent mean absolute deviation（PMAD）．ConclusionThe results indicate that the PSO-BPNeural Networks is better than MLR in forecasting PM10．This research can provide some methodological references for forecasting ambient particulate matter．

MLRmodel；PSO-BP；PM10；Meteorology factor；Forecasting

*國家自然科學基金項目（81573249）；廣東省自然科學基金（2016A030313530）

△通信作者：歐春泉，E-mail：ouchunquan＠hotmail．com