某超高層框架-核心筒結構時變效應分析與實測

吳 杰, 劉俊杰

(同濟大學 土木工程學院, 上海 200092)

某超高層框架-核心筒結構時變效應分析與實測

吳 杰, 劉俊杰

(同濟大學 土木工程學院, 上海 200092)

建立某巨型支撐外框架-核心筒超高層結構的空間有限元模型, 基于CEB-FIP(1990)模型計算混凝土收縮徐變效應, 按實際工況考慮施工分層加載的影響, 分析該結構在實際荷載作用下的豎向位移效應, 并將計算結果與現場實測數據進行了對比分析. 結果表明: 收縮徐變效應對該結構的豎向變形影響較大, 框架柱與核心筒的時變性能差異將產生較大的層間位移差; 考慮收縮徐變的施工過程分析可以較準確地模擬超高層框架-核心筒結構的豎向位移狀況.

超高層結構; 施工過程分析; 收縮徐變; 結構監測

在高層建筑結構施工過程中, 塔樓結構的變形主要來源于自重恒荷載和施工活荷載; 當施工完成后, 其變形來源于裝飾面層、隔墻等非結構性構件荷載以及使用階段的活荷載. 溫差效應及長期、短期沉降差和混凝土的收縮、徐變等非荷載作用對高層建筑變形產生的影響將貫穿整個施工和運營過程.

高層建筑的結構自重往往達到總豎向荷載的80%以上, 并隨著施工過程逐層增加. 在每層施工中, 樓層標高逐層找平, 抵消已經發生的壓縮變形. 因此, 高層混凝土框架結構在豎向荷載作用下的豎向變形遠小于考慮整個結構完成后一次加載計算所得到的結果[1]. 混凝土隨著作用在其之上壓應力的持續, 將持續發生徐變變形. 對超高層建筑而言, 混凝土的加載齡期較短, 增強了其徐變變形; 變形隨高度發生的累積效應比較明顯; 不同的豎向構件因使用功能上的不同導致壓應力水平差異較大, 從而使豎向構件間累計徐變變形差異變大. 這些因素都會對結構產生不利的影響[2]. 另外, 混凝土發生徐變時, 通常伴隨著收縮變形的產生, 其變形規律接近徐變變形, 且與徐變變形同向, 兩者疊加后加大了豎向構件的后期變形, 使超高層建筑結構豎向構件在后期由非荷載引起的塑性變形不容忽視[3].

本文針對天津117大廈, 建立其考慮收縮徐變效應的有限元模型, 進行施工全過程數值模擬計算, 并與現場實測結果進行對比分析, 研究時變效應對超高層框架-核心筒結構的影響.

1 混凝土時變模型

在建筑結構施工過程中, 結構時變、材料時變、荷載時變等將對結構受力性能產生影響, 其中, 收縮徐變是混凝土材料時變的重要組成部分. 目前國內外學者已經提出了一些混凝土收縮徐變模型, 其中應用較多的有CEB-FIP(1990)模型、ACI209模型、GL-2000模型、JTJ-85模型和JTGD62-2004模型等[4].

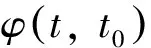
(1)

(2)

(3)

(4)

(5)

(6)

(7)

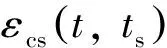
(8)

(9)

(10)

(11)

(12)

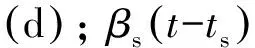
2 工程實例分析

2.1 工程概況

天津117大廈工程位于天津市高新區, 建筑高度(至頂部停機坪)約為597 m, 共117層, 建筑效果圖如圖1所示. 塔樓平面為正方形, 外形隨高度變化, 各層周邊建筑輪廓隨著斜外立面逐漸變小, 樓首層建筑平面尺寸約65 m×65 m, 漸變至頂層時平面尺寸約45 m×45 m. 中央混凝土核心筒為矩形, 平面尺寸約37 m×37 m. 塔樓結構受力體系由外框架+核心筒組成, 如圖2所示. 外框架柱為異形鋼管混凝土柱, 截面形狀如圖3所示, 柱截面面積等效半徑從3 720 mm沿豎向變化至906 mm. 柱與框架梁、板通過鋼筋混凝土環梁套接, 核心筒主要用作高速電梯設備用房和服務用房[7].

2.2 計算模型

應用Midas軟件建立天津117大廈有限元模型. 其中: 1～34層為C70混凝土, 34～65層為C60混凝土, 65層以上為C50混凝土, 鋼材為Q345; 核心筒和樓板采用板單元, 鋼筋混凝土柱和鋼梁采用梁單元. 構件截面尺寸、樓板厚度均按實際情況建立. 模型中共有節點18 350個, 梁單元24 474個, 板單元143 472個. 本文考慮結構自重作為恒荷載, 由于施工活荷載和使用條件下活荷載等非長期荷載對結構時變效應不明顯, 對結構豎向構件變形產生的影響也不是很顯著, 故在本文分析中未做考慮.

圖1 建筑效果圖Fig.1 Architectural rendering

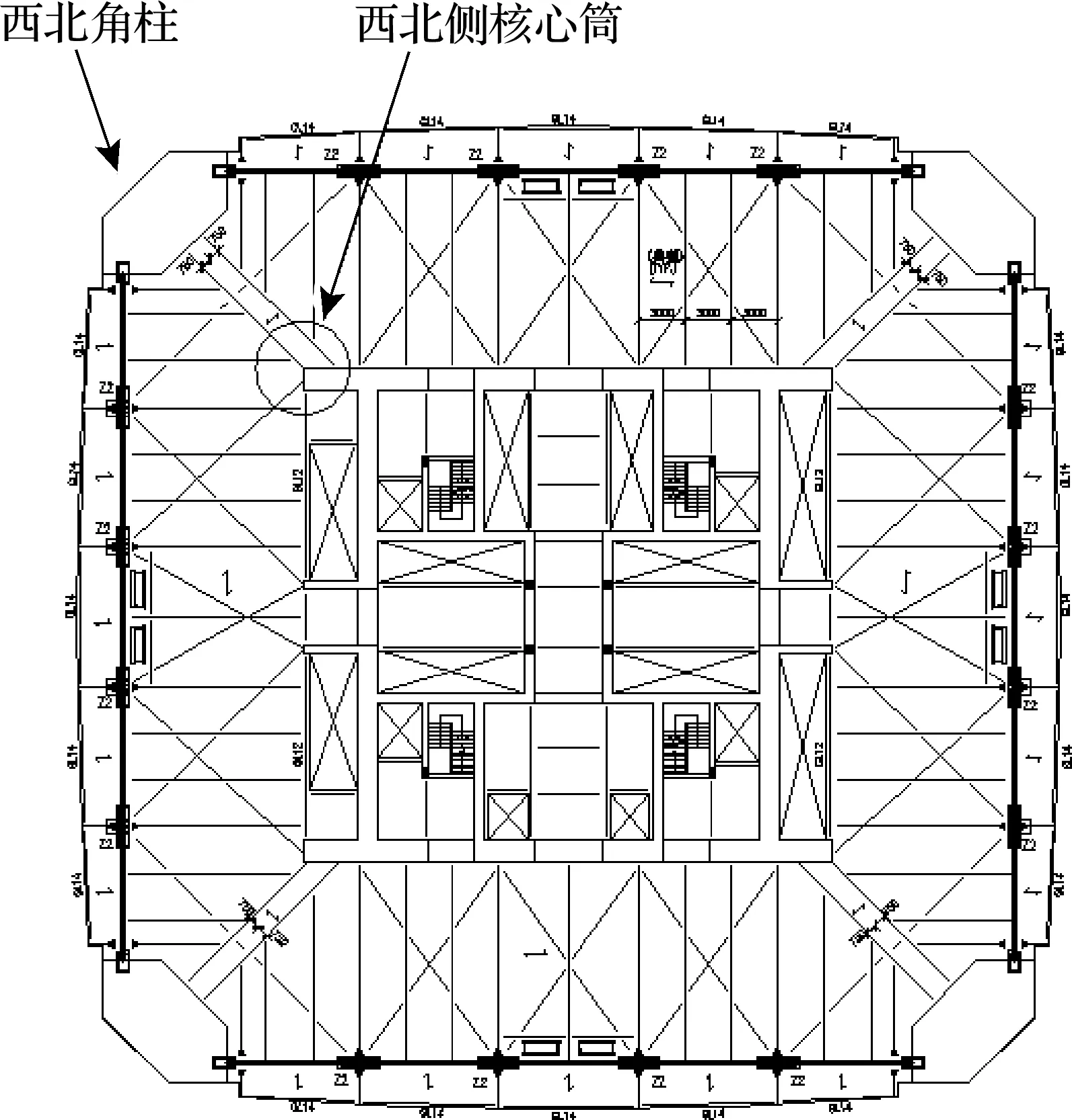
圖2 塔樓平面圖Fig.2 Plan sketch of tower building

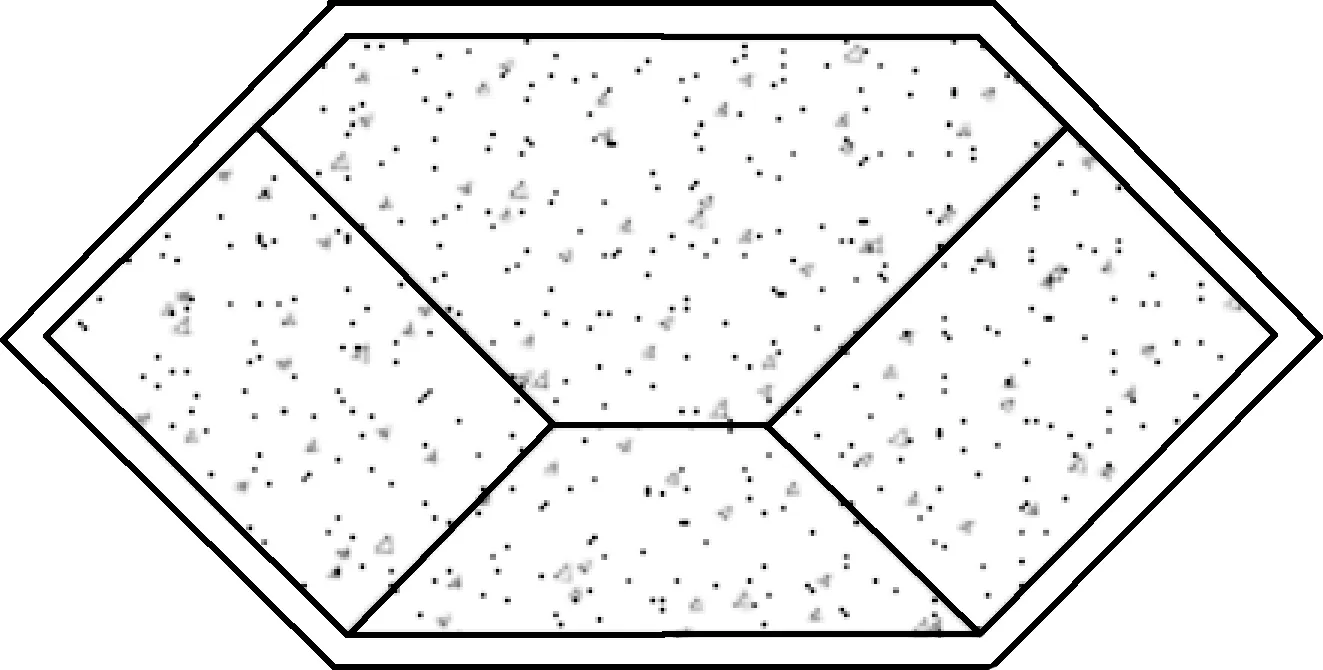
圖3 異形鋼管混凝土框架角柱截面Fig.3 Special-shaped concrete-filled steel tube section of frame angle column

為了對施工變形發展規律進行預測, 需對結構的施工過程進行模擬計算. 按照現場工程施工記錄, 并結合實際監測數據的時間點, 模擬實際施工中結構的逐層搭建和加載過程[8]. 結構封頂前共建立了35個施工子步并依次激活, 主要定義了外框架、核心筒、內外樓板. 子步間的時間跨度約為1個月, 每個子步的塔樓提升約3～4層, 核心筒與框架間保持15層的高差. 結構封頂后增加了9個時間施工步, 分別為封頂后1/12、1/6、1/4、1/2、1、2、4、7和10年. 計算開始時間為2012-10-31, 主體結構封頂完成時間為2015-09-08(1 042 d), 計算終止時間為2025-09-30(4 717 d).

施工過程計算中, 考慮混凝土隨時間變化的收縮徐變效應, 計算條件設定如下: 收縮徐變采用CEB-FIP(1990)模型, 水泥采用普通硅酸鹽水泥; 長期荷載作用時混凝土齡期為10 d; 混凝土與大氣接觸時的齡期為3 d; 混凝土養護條件下的相對濕度為80%. 混凝土抗壓強度隨時間變化采用歐洲規范CEB-FIP(1990)模型的相關公式[9].

結構外框架角柱為異形鋼管混凝土截面, 截面形狀如圖3所示.由于鋼管混凝土內鋼管與混凝土為復雜的多向應力狀態, 為簡化計算, 假定混凝土與鋼管之間黏結可靠, 協同工作, 且忽略鋼管與混凝土的徑向作用力, 核心混凝土按單軸受力分析[10].有限元建模時分別建立鋼管和混凝土單元, 通過單元兩端共節點來模擬鋼管和混凝土的共同工作[11].

2.3 施工過程計算結果及分析

應用Midas軟件對施工全過程進行數值模擬計算, 按結構實際施工進度考慮收縮徐變效應, 選取西北角柱和西北側核心筒的位移結果進行分析. 具體位置如圖4所示.

2.3.1 框架柱豎向位移

塔樓西北角柱在結構封頂和使用10年后的豎向位移大小隨樓層變化如圖4所示. 由圖4可知, 豎向位移隨樓層增加呈魚腹形狀. 其原因是當樓層較低時, 雖然其上部荷載比較大, 但位移積累較小, 故豎向變形較小; 頂部樓層在樓層找平時會抵消之前發生的豎向位移, 故而豎向位移亦較小. 結構封頂后, 恒荷載不再增加, 但收縮徐變變形仍在繼續發展, 故頂部豎向位移在投入使用后的10年間有了較大的發展, 如圖4(b)所示.

由圖4還可知： 結構封頂時角柱豎向變形峰值出現在第55層, 數值為55.2 mm, 其中, 收縮及徐變變形之和為17.2 mm, 占總變形的31.2%; 使用10年后角柱豎向變形峰值出現在第66層, 數值為69.3 mm, 其中, 收縮及徐變變形之和為32.1 mm, 占總變形的46.3%.

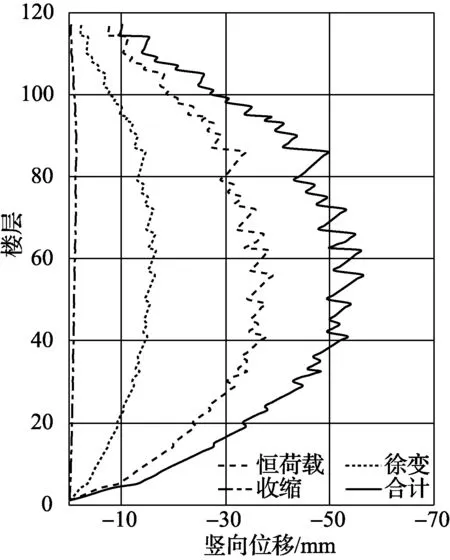
(a) 結構封頂

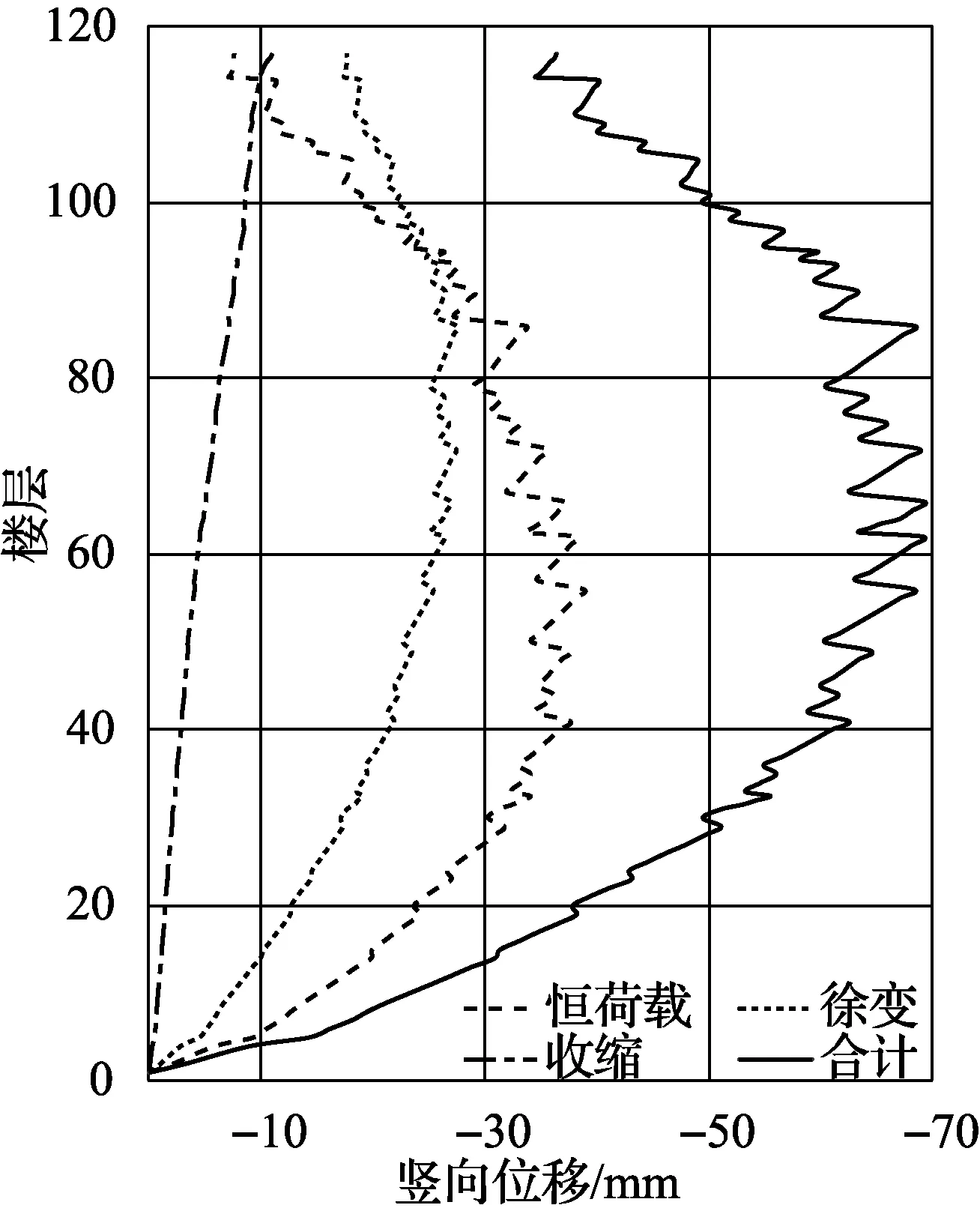
(b) 使用10年圖4 西北角柱豎向位移Fig.4 Vertical displacement of northwest angle column

2.3.2 核心筒豎向位移

塔樓西北側核心筒在結構封頂時和使用10年時的豎向位移大小隨樓層變化如圖5所示. 由圖5可知: 核心筒的樓層-豎向位移曲線亦成魚腹形狀; 結構封頂時核心筒豎向變形峰值出現在第72層, 數值為71.0 mm, 其中, 收縮及徐變變形合計為33.7 mm, 占總變形的47.5%; 使用10年后核心筒豎向變形峰值出現在第87層, 數值為108.7 mm, 其中, 收縮及徐變變形之和為78.5 mm, 占總變形的68.6%.

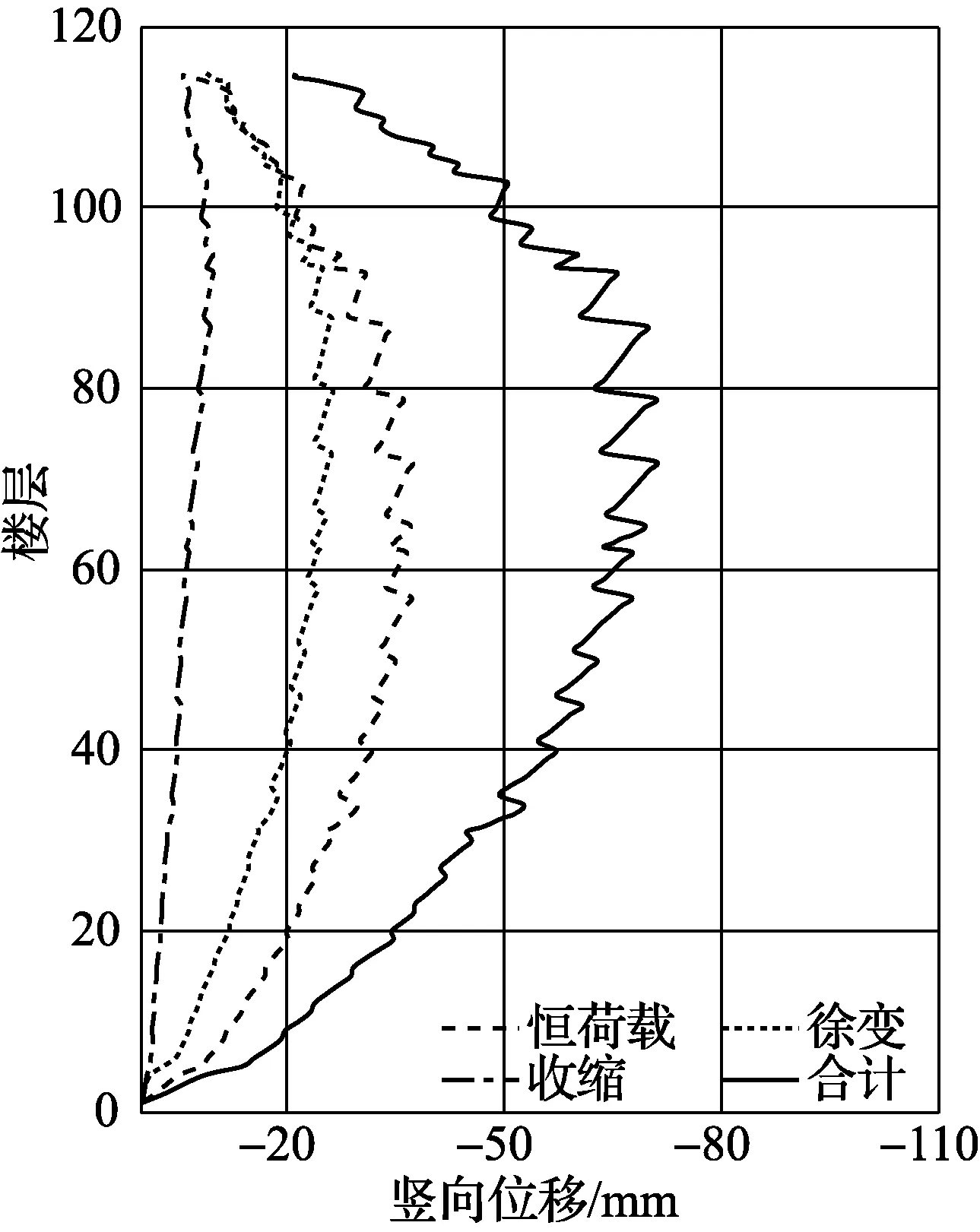
(a) 結構封頂

較之角柱, 核心筒的豎向位移數值更大, 峰值所在樓層更高. 其中, 收縮變形帶來的角柱豎向位移峰值為11.0 mm, 核心筒豎向位移峰值為39.1 mm, 核心筒的位移峰值遠遠大于角柱的位移峰值. 這是因為角柱截面為鋼管混凝土構件, 混凝土由于受到鋼管的約束, 與空氣間的水分交換速率減緩, 所以收縮應變較小; 反之核心筒混凝土的構件厚度較小, 與空氣接觸面大, 收縮應變較大. 由于核心筒單位時間內的收縮徐變位移更大, 使得樓層豎向位移的累積效應更加顯著, 從而使得豎向位移峰值出現在較高的樓層.

2.3.3 混凝土柱與核心筒豎向位移差

塔樓角柱與核心筒在結構封頂時與使用10年時的豎向變形差值隨樓層變化如圖6所示, 負值代表核心筒豎向位移大于角柱. 由圖6可知: 核心筒與角柱的豎向位移差幾乎全部由收縮徐變變形貢獻, 結構封頂時該差值的峰值出現在83層, 為-28.5 mm; 使用10年后該差值的峰值出現在102層, 為-49.0 mm. 由此可見, 收縮徐變會使框架與核心筒之間產生較大的豎向位移差, 而該差值會引起較大的附加彎矩和附加剪力, 在實際工程設計中應加以考慮[12].

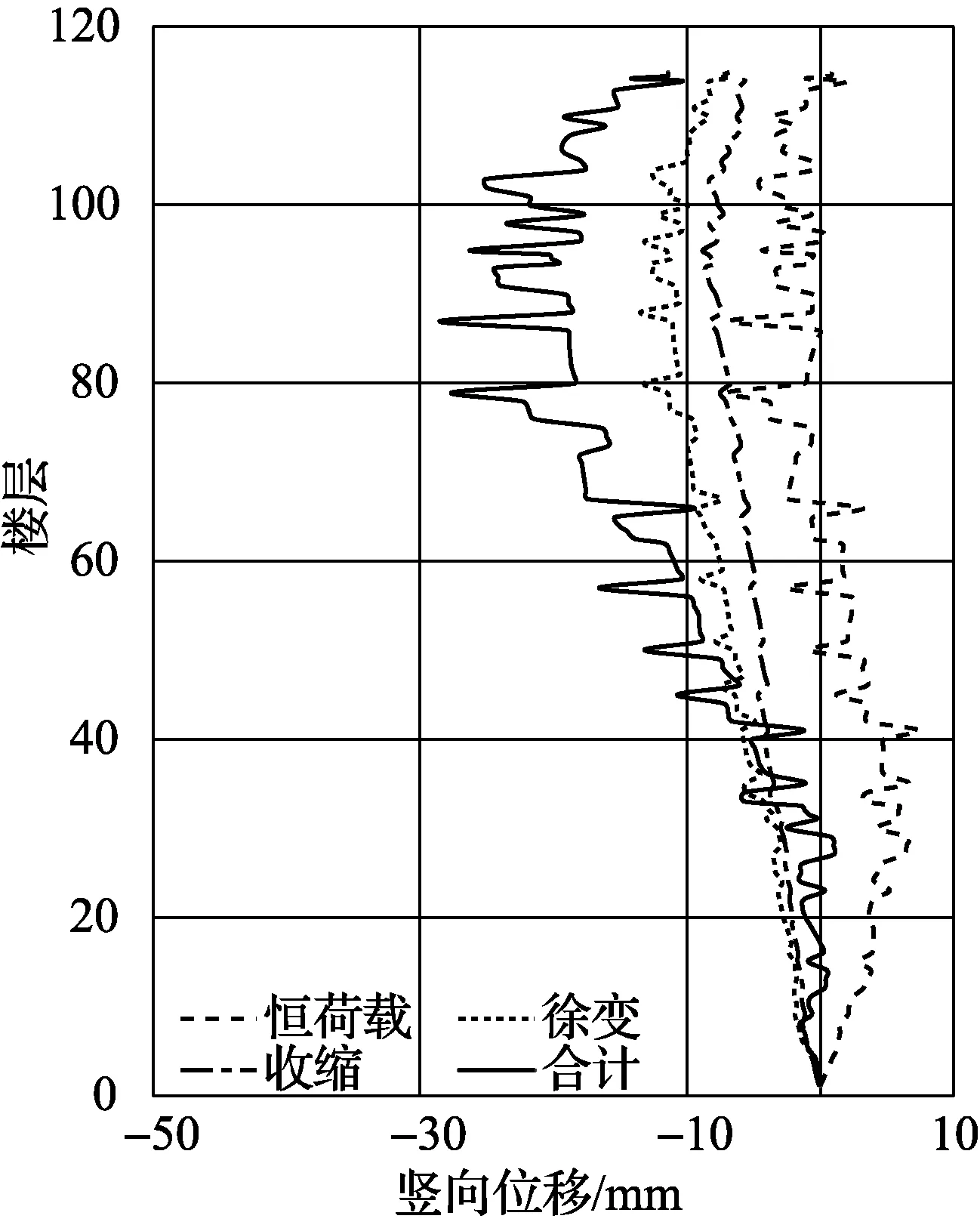
(a) 結構封頂

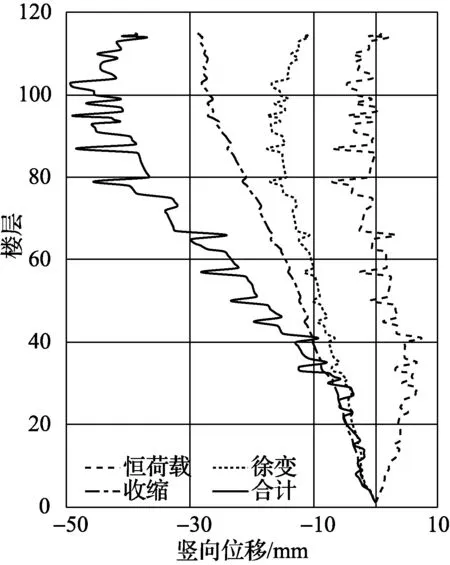
(b) 使用10年圖6 核心筒-角柱豎向位移差Fig.6 Vertical displacement difference of angle column and core tube

2.4 施工模擬結果與實測標高對比及分析

為驗證理論計算的正確性, 對大樓的豎向變形進行了5次現場實測, 時間分別為2015-01-30、2015-03-25、2015-05-14、2015-09-23和2015-12-18. 測量樓層分別為第18、26、34、42和50層. 其中, 核心筒測點每層8個, 外框架測點每層4個, 如圖7所示. 為減少測量誤差影響, 以下取各樓層測點的平均位移值進行對比分析. 選取2015-01-30作為基準時間點, 假定該時刻的位移實測值與計算值相同, 繪制時間-位移增量圖.

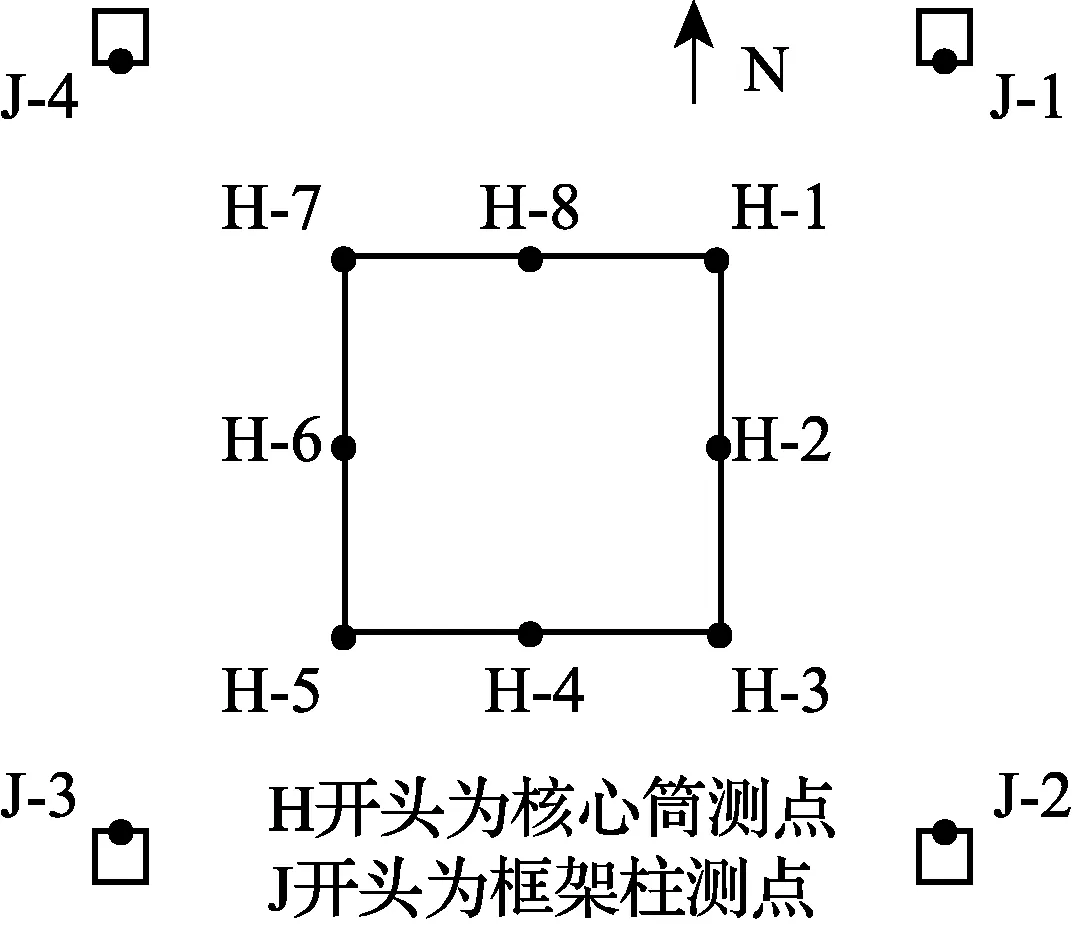
圖7 測點布置示意圖Fig.7 Measuring point arrangement

結構封頂時間為2015-09-08(1 042 d), 為了說明在整個結構建造及使用過程中位移增量的趨勢, 34層核心筒測點從開始建造直至使用10年時刻的豎向位移發展趨勢如圖8所示. 由圖8可以看出, 臨近結構封頂時, 塔樓建造進度是逐漸放緩的, 故2015年是豎向位移發展由快變慢的一年.

圖8 第34層核心筒豎向位移發展趨勢圖Fig.8 Tendency of vertical displacement development of core tube at 34F

圖9為2015年第18、26、34、42和50層的時間-豎向位移增量對比圖, 其中橫坐標為結構累計施工天數. 第823天對應2015-01-31; 第1 042天對應2015-09-08, 即結構封頂時間; 第1 156天對應于2015-12-30.

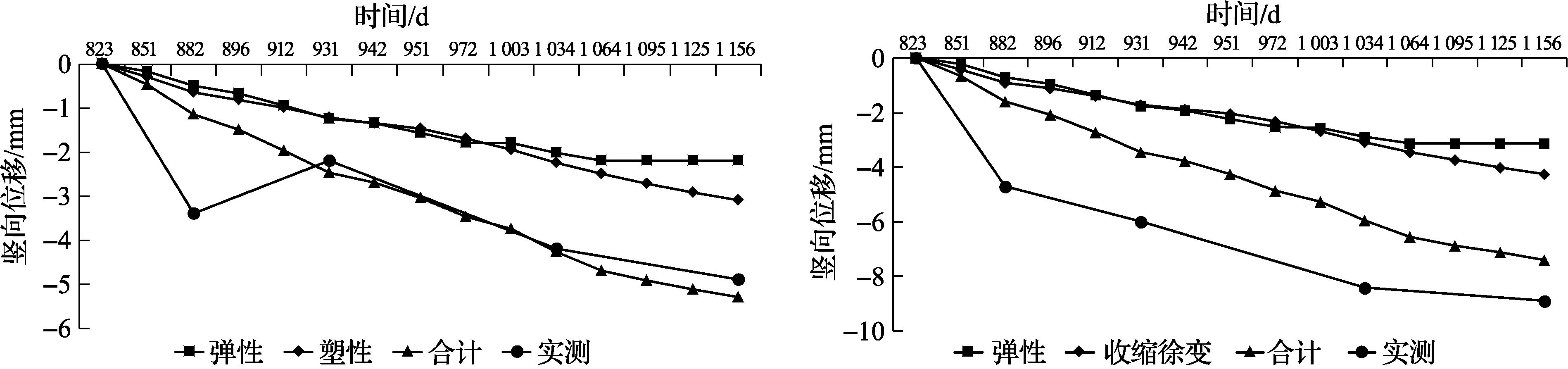
(a) 第18層核心筒測點 (b) 第26層核心筒測點

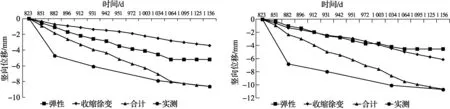
(c) 第26層框架角柱測點 (d) 第34層核心筒測點

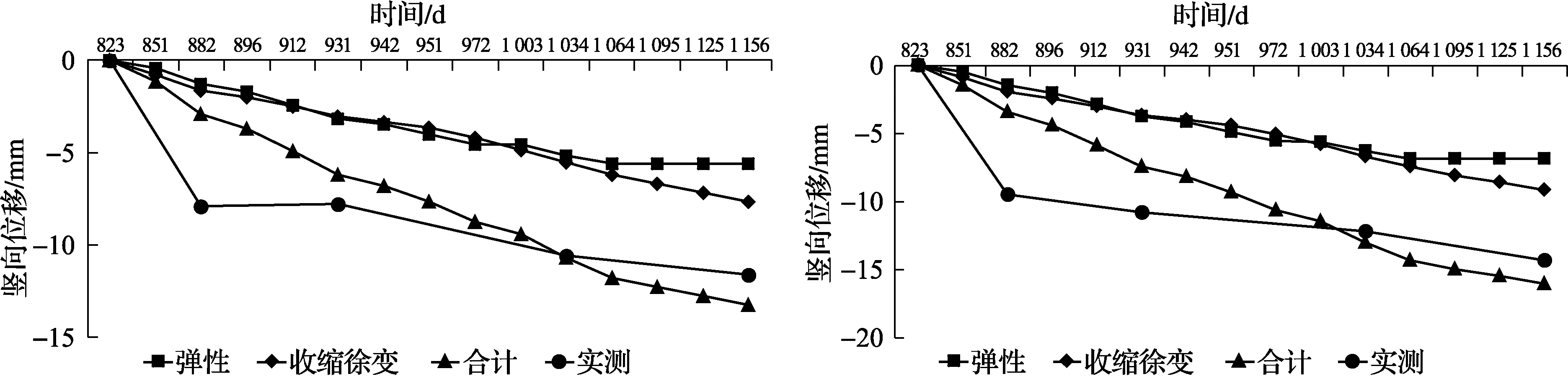
(e) 第42層核心筒測點 (f) 第50層核心筒測點圖9 不同位置豎向位移增量圖Fig.9 Increment of vertical displacement development at different position

3 結 語

本文針對天津117大廈進行施工全過程數值模擬計算和現場實測對比分析, 研究時變效應對超高層框架-核心筒結構的影響, 得出以下主要結論:

(1) 共節點雙單元模型能用于鋼管混凝土構件的施工全過程數值模擬, CEB-FIP(1990)時變模型具有較好的計算精度；

(2) 由于構件收縮徐變效應的差異, 框架與核心筒之間將產生較大的豎向位移差, 實際工程設計中應考慮該影響；

(3) 結構彈性位移與實測結果相差較大, 考慮時變效應后, 核心筒與框架角柱豎向位移的理論值和實測值基本一致, 表明超高層框架-核心筒結構的收縮徐變效應不能忽略, 設計和施工中需予以考慮.

[1] 陳富生, 邱國樺, 范重. 高層建筑鋼結構設計. 北京: 中國建筑工業出版社, 2000: 296-297.

[2] 高層建筑混凝土結構技術規程: JGJ 3—2010 [S].

[3] 楊誠. 某超高層考慮混凝土徐變收縮的施工模擬分析[J]. 廣東土木與建筑, 2013 (6): 14-16.

[4] 楊小兵. 混凝土收縮徐變預測模型研究[D]. 武漢: 武漢大學土木工程學院, 2004.

[5] DEZI L, LEONI G, TARANTINO A M. Time-dependent analysis of prestressed composite beams[J]. Journal of Structural Engineering, 1995, 121(4): 621-633.

[6] 孟江, 趙寶俊, 劉建梅. 混凝土收縮徐變效應預測模型及影響因素[J]. 長安大學學報(自然科學版), 2013, 33(2): 56-62.

[7] 劉鵬, 殷超, 李旭宇, 等. 天津高銀 117 大廈結構體系設計研究 [J]. 建筑結構, 2012, 42(3): 1-9.

[8] 彭明祥, 劉軍進, 王翠坤, 等. CCTV主樓施工過程結構關鍵點位的變形監測技術[J]. 建筑科學, 2009, 25(11): 91-94.

[9] Comite Euro-international Du Beton. CEB-FIP model code [S]. London: Thomas Telford Publishing, 1993.

[10] 張電杰, 王元豐, 雷揚. 鋼管混凝土軸心受壓短柱徐變模型研究[J]. 土木工程學報, 2010, 43 (增刊2): 246-251.

[11] 劉俊, 吳杰, 羅曉群, 等. 高層鋼管混凝土結構施工全過程數值模擬[J]. 土木建筑與環境工程, 2012, 34(5): 50-56.

[12] 張其林, 呂佳, 李晗, 等. 上海中心大廈施工過程數值分析與監測研究[J]. 施工技術, 2013, 42(15): 9-12.

Time-Dependent Analysis and Field Test for a Frame-Core Tube Super High-Rise Structure

WUJie,LIUJun-jie

(College of Civil Engineering, Tongji University, Shanghai 200092, China)

Based on the consideration of concrete creep and shrinkage with CEB-FIP (1990) model, and the influence of actual construction process, a spatial finite element model of giant support frame drum-core tube super high-rise structure was established and analysis on the vertical displacement of its components under vertical loads was conducted. Analysis results were compared with those obtained by field test. The test and analysis results show that creep and shrinkage can exert great influence on vertical displacements of this structure, and besides frame column and core tube will have an obvious deformation differences between floors. Furthermore, construction progress analysis that takes creep and shrinkage into account can accurately simulate the vertical displacement state for this type of super high-rise structures.

super high-rise structure; construction progress simulation; creep and shrinkage; structural monitoring

1671-0444 (2016)04-0559-07

2016-04-27

上海市自然科學基金資助項目(16ZR1438900)

吳 杰(1975—)，男，安徽無為人，副教授，博士，研究方向為結構施工控制和數值模擬. E-mail: wj536@163.com

TU 973.2

A