多直線目標的影像畸變計算

胡亞江，沙月進

(1.深圳中銘勘測股份有限公司，廣東 深圳 518172； 2.東南大學交通學院，江蘇 南京 210096)

多直線目標的影像畸變計算

胡亞江1*，沙月進2

(1.深圳中銘勘測股份有限公司，廣東 深圳 518172； 2.東南大學交通學院，江蘇 南京 210096)

對于未知來源或未知攝影機攝取的近景影像，通過提取影像上多個直線目標，恢復其曲線構像為直線的過程來計算影像畸變。首先分析影像畸變類型，確定影像畸變模型，然后采用二分法進行多個直線目標影像畸變的計算方法。經過室內、室外場地的實例計算，該方法計算得到的影像畸變參數與三維鑒定場計算的結果非常接近。試驗表明該方法可行，能滿足小像幅圖像解算的精度要求，適用于歷史影像及未知來源的影像解算和糾正。

影像畸變；多直線目標；多源影像；曲線構像；二分法

1 引 言

傳統攝影機的標定是以攝影機為標定對象的，不管是在攝影前或攝影后進行，標定過程都必須對攝影機實體本身來進行。普通數碼相機屬于非量測攝影機，利用其圖像進行圖像測量時，物鏡畸變直接影響到圖像測量的精度，物鏡畸變系數的計算成為非量測攝影機標定的主要內容。在攝影測量和計算機視覺領域，許多學者對此進行過深入研究。

典型的研究成果包括：利用旋轉矩陣的正交條件和非線性最優化進行相機標定(張正友，1998)；利用二維DLT及光束法相結合進行相機標定(張永軍等，2002)；利用全線性標定方法和矢量分析法進行快速標定多相機的標定(周富強，邾繼貴，2003)；單幅影像上利用直線約束檢校相機內方位元素(Heuvel，1999)。

生活中的近景影像的獲取途徑是多樣化的，有歷史圖片、異地獲取并傳輸的圖像、各種攝影設備獲取的圖像、視頻的取幀圖像。對于這些多源近景圖像，在影像解析和測量中通常無法了解其攝影設備，通過對攝影機標定來獲取物鏡畸變參數就不可行。

為了全面描述數碼影像的畸變，這里采用影像畸變的概念來概括數碼影像所包含的物鏡畸變和電子畸變。影像畸變是影響非量測攝影機圖像測量精度的主要因素。在已知條件不足的情況下，要獲取影像的畸變參數信息，只能從影像本身提取目標隱含的幾何信息來實現。

2 影像畸變模型

2.1 物鏡畸變

物鏡畸變參數是攝影機畸變的主要內容之一，對日益廣泛使用的非量測CCD相機來說，標定是從二維圖像獲取三維信息必不可少的步驟(于寧鋒，2007)。

目前，通用的物鏡畸變解算模型見式(1)，該數學模型通過建立標定場地的方法精確計算畸變系數k1、k2、k3、p1和p2。

(1)

Capitania(GianCarloCapitania等，2006)用圖示的形式表達了畸變的五個影像類型，如圖1所示。

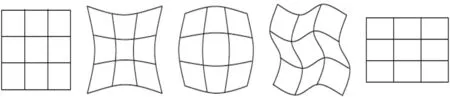
圖1 物鏡畸變影像類型(Gian Carlo Capitania 等，2006)

根據應用場合和精度要求的不同，國內外的很多學者做過大量的研究認為：由于在考慮非線性畸變時對攝像機標定需要使用非線性優化算法，引入過多的非線性參數(如上述模型的第二項與第三項)，往往不僅不能提高精度，反而引起解的不穩定(RYTsai.，1986)。一般情況下，上述非線性模型的第一項徑向畸變已能足夠描述非線性畸變(劉傳才，2002)。引入上式中第二項與第三項在使用廣角鏡頭時能提高模型的精度(ODFaugeras，G.Toscani1987；Weng，1990)。對于小像幅數碼圖像，第一項中的第一部分k1的影響又遠遠大于k2、k3兩部分的影響，通常只考慮畸變參數k1一項。本文研究的影像畸變是以式(2)為解算模型。

(2)

2.2 影像畸變特點

影像畸變就是物鏡畸變在攝影影像上的具體體現，是依賴于物鏡畸變而又獨立存在的影像參數。同物鏡畸變相比，影像畸變具有以下幾個特點：

(1)影像畸變主要來源于物鏡畸變，常規處理方法是在攝影前或攝影后對攝影機進行標定，計算出物鏡的畸變系數，用物鏡畸變來消除影像畸變。

(2)物鏡畸變的標定都必須通過建立三維或二維標定場地進行標定來實現，而影像畸變無需標定場地，從攝影目標的幾何信息中計算影像畸變系數。

(3)影像畸變參數可以脫離攝影機本身單獨存在。尤其是對于未知來源的歷史圖像、網絡傳輸圖像、視頻幀圖像，在不知道何種類型攝影機的情況下，其影像畸變不僅存在而且是可以解算得到的。

(4)影像畸變包含了不受物鏡影響的電子畸變。

3 多直線目標的畸變計算原理

3.1 計算原理

畸變的存在使直線目標的構像變為曲線(馮文灝，商浩亮，侯文廣，2006)，如果被攝目標的某個邊界是確定的直線線段，其在影像上的成像理論上也必定是直線。然而，影像畸變的存在使其成像變成了曲線。

如圖2 ，在圖像范圍內選擇成像清晰、邊界明顯的直線目標，在直線目標的起點A、中點B和終點C各選擇一點，量測其像素坐標，由于物鏡畸變的存在，A、B、C三個點不在一條直線上，以圖2中桶形畸變為例加以說明。

假定中間點B受影像畸變引起的向徑變化為△rb，根據假定的畸變向徑可以計算假定的影像畸變系數：

k1=△rb/(rb+△rb)3

(3)

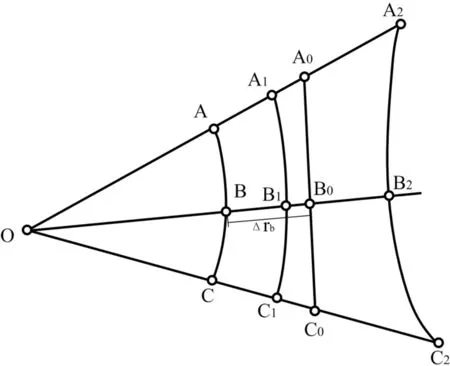
圖2 影像畸變計算原理

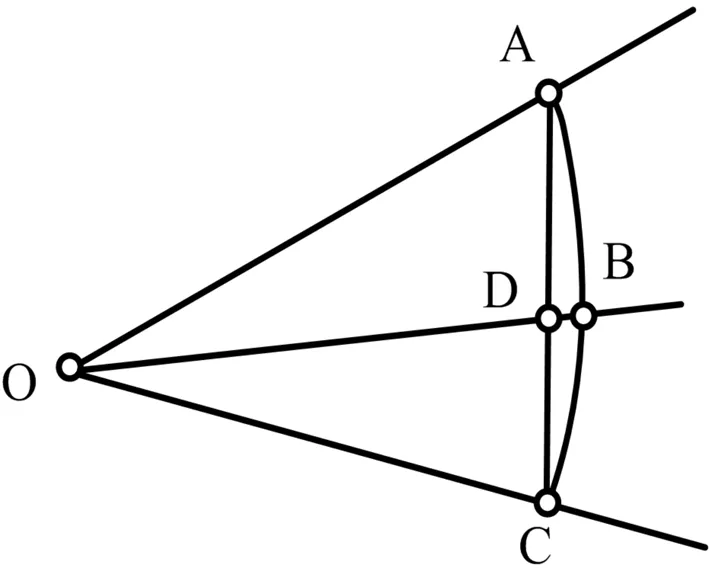
圖3 影像畸變類型判斷圖解

進一步利用假定的影像畸變參數計算A、B、C三點的理想位置A′、B′、C′的向徑：

(4)

消除假定的影像畸變后，A′、B′、C′的正確位置的像素坐標：

(5)

由于B的向徑改正為△rb及其影像畸變系數都是假定的，使得消除影像畸變后A′、B′、C′三點一般不滿足三點共線的條件，可能出現以下三種情況：

(1)如果假定的△rb比正確值小了，消除影像畸變后的位置為圖2中的A1、B1、C1，三點的幾何關系仍是桶形畸變；

(2)如果假定的△rb比正確值大了，消除影像畸變后的位置為圖2中的A2、B2、C2，三點的幾何關系變是枕形畸變；

(3)如果假定的△rb與正確值一致，消除影像畸變后的位置為圖2中的A0、B0、C0，這三個點共線。

可見，根據直線目標改正后是否為一直線可以用來判斷中間點假定的畸變向徑是否正確。這里存在兩個技術難點：一是改正后的目標是否為直線以及彎曲類型的判斷；二是中間點的假定畸變向徑的確定。

3.2 影像畸變類型的判斷

影像畸變計算中，判斷A、B、C三點和A′、B′、C′三點的畸變類型及是否共線是關鍵內容，可采用以下步驟來實現：

① 利用A、B、C三點的像素坐標計算AC和OB的交點D的像素坐標；

② 計算OD、OB的距離；

③ 若ODOB，影像存在枕形畸變。

3.3 二分法確定中間點畸變向徑

從上面的介紹可以知道：計算B點受影像畸變引起的向徑變化△rb是計算影像畸變參數的關鍵。由于無法直接知道△rb的值，通過二分法進行趨近計算，具體計算過程如表1中各步驟進行：

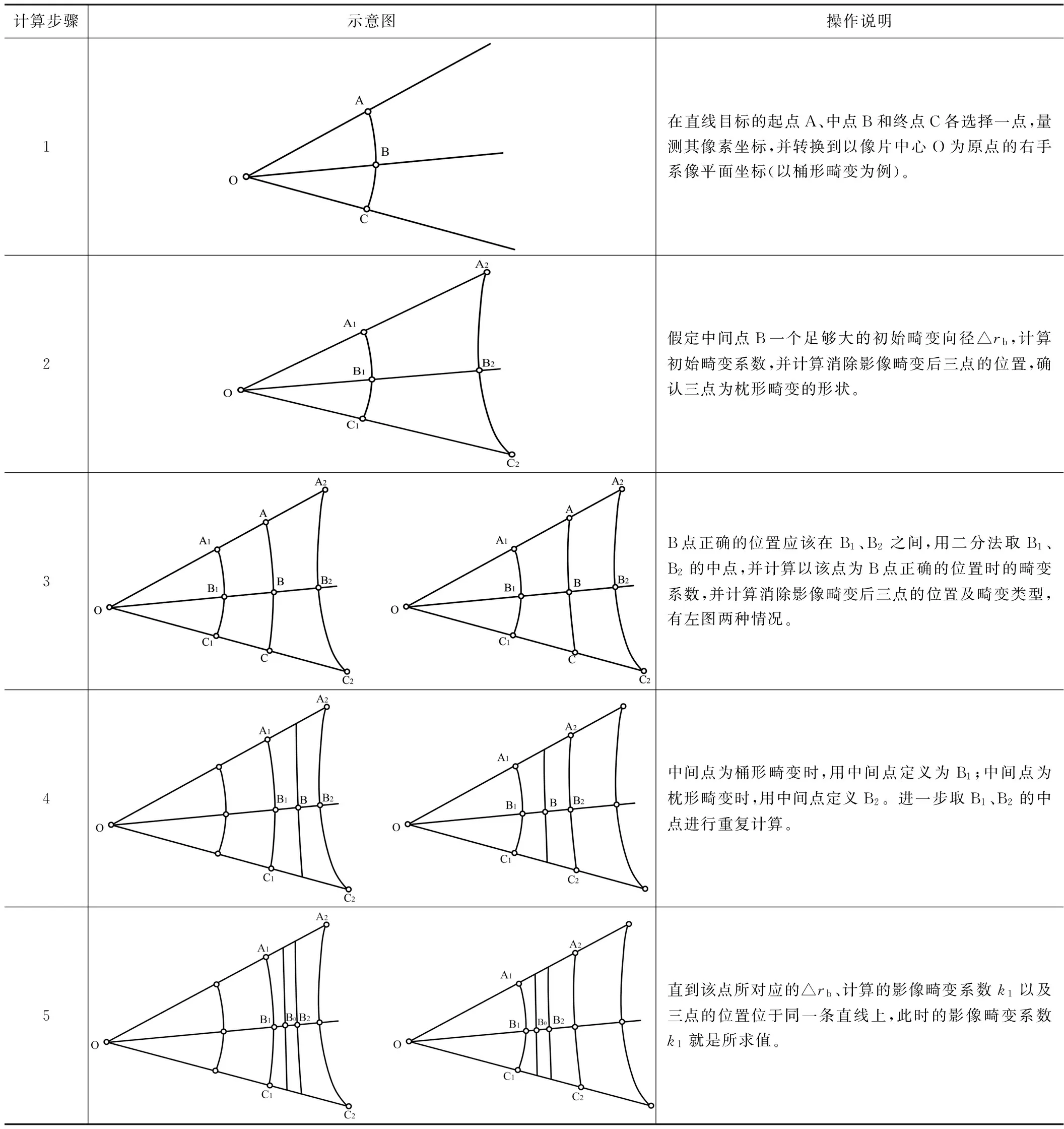
影像畸變參數計算過程 表1

3.4 影像畸變計算的程序流程

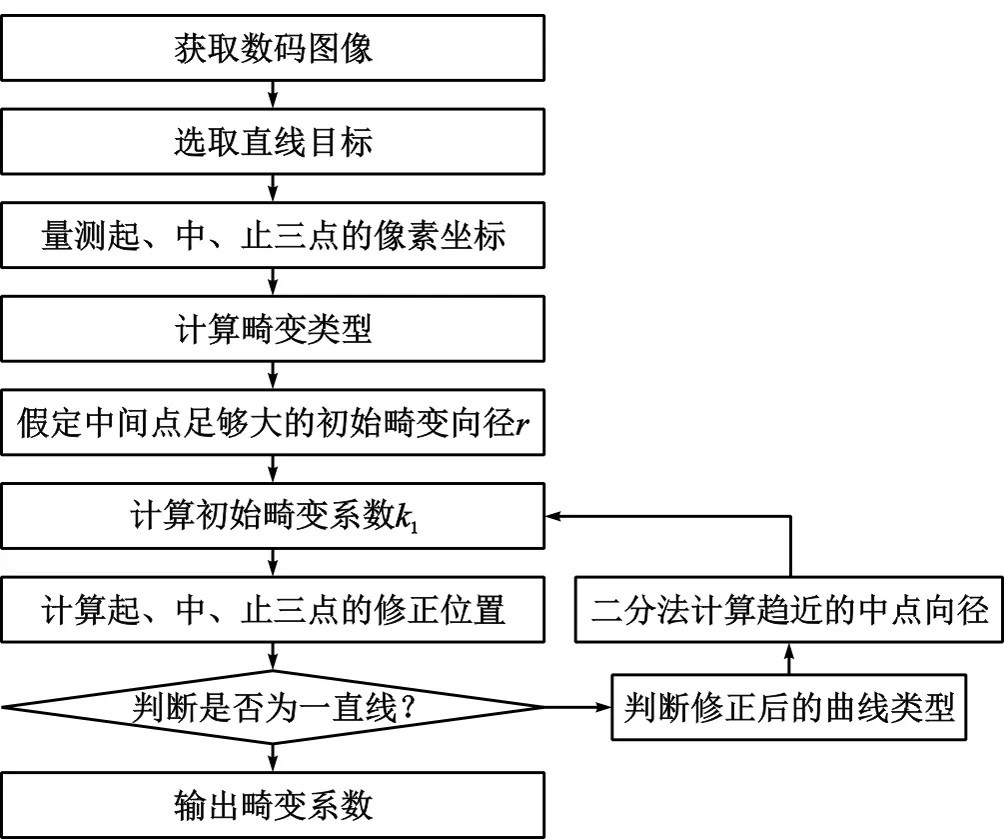
圖4 影像畸變參數計算流程圖

3.5 影像畸變計算的具體要求

本算法在實際操作中要注意以下幾個方面：

(1)要選擇確認的直線目標作為計算的依據；

(2)直線目標要避免通過像片中心；

(3)直線目標盡可能均勻分布在影像的各個位置。

4 實例計算與結果分析

4.1 室內試驗場計算

在室內嚴格垂直的兩個墻面上，精確固定兩張帶有 100 mm格網的高精度聚酯薄膜紙(如圖5所示)，精確測量72個格網點的空間三維坐標，聚酯薄膜紙的分米格網測量精確到 0.2 mm，建立精密室內試驗場。

圖5 室內試驗場計算影像畸變

應用攝影測量軟件精確量取上圖影像上的72個格網點像點平面坐標，精確到0.5個像素。并對上圖影像畸變參數進行嚴密平差計算，得到的影像畸變參數為2.21×10-8。然后采用多直線目標的方法來解算該影像的畸變參數：選取了圖5中的12個直線目標，計算結果如表2所示。

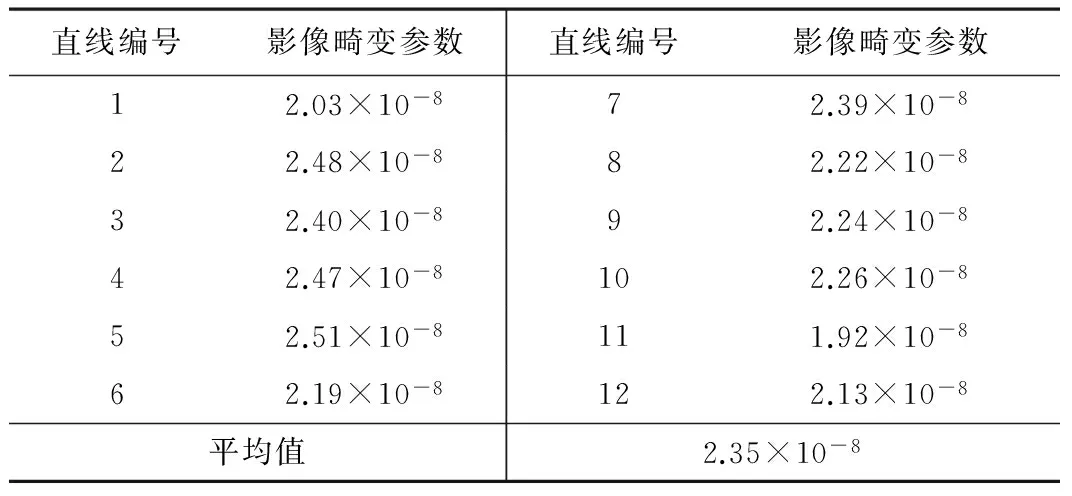
室內試驗場計算結果 表2

通過對12個直線目標的計算結果均值為結果2.35×10-8，影像畸變參數的較差值△k1為小值，試驗結果與三維控制場的計算值非常接近，效果良好。

4.2 室外場地計算

在圖6中，對(a)中的近景影像求解其畸變參數，從影像中選取了4條明顯的建筑物邊緣作為直線目標。通過精密全站儀實地測量直線目標上點的空間坐標，應用攝影測量軟件量測直線目標上的點的像點坐標。計算得到影像畸變參數平均值為1.84×10-8。

室外場地與室內場地的計算結果有一定的差值，但是與事先通過專業的室內三維鑒定場鑒定的相機畸變參數值1.98×10-8較為接近，影像畸變參數的偏差值△k1為小值，對像點坐標的影響值在1個像素以內。

上述相機三維鑒定場系東南大學測繪工程系專用的室內三維鑒定場，試驗開始前通過對鑒定場多個角度拍攝得到的像片進行平差計算，得到該試驗的相機畸變參數均值作為本試驗影像畸變參數的參考值。

(a)實地近景影像及其直線目標

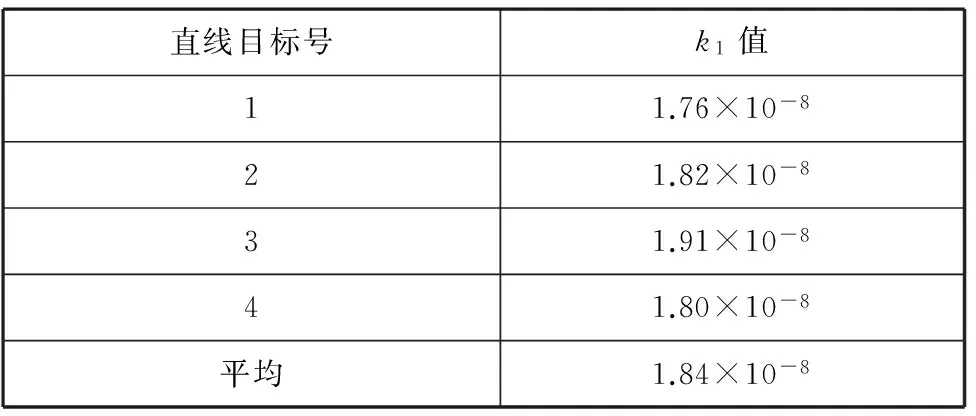
直線目標號k1值11.76×10-821.82×10-831.91×10-841.80×10-8平均1.84×10-8

(b)影像畸變計算結果

圖6 室外多直線目標影像畸變算例

4.3 試驗結果分析

(1)根據像點坐標的改正公式，可推算出影像畸變參數偏差△k1對像點坐標改正的影響值。

(6)

上式中r表示向徑，即像點與自準直主點之間的距離，其計算式如下：

(7)

試驗中使用的SONYDSC-HX300相機，其分辨率 1 920×1 080像素。根據(7)式可計算出位于像片4個角點處的最大向徑值r=1101.45像素。試驗中畸變參數計算值與參考值的偏差值△k1=0.14×10-8，根據式(6)計算出其對像點坐標的最大影響值：

可以看出上述試驗算例中的影像畸變參數計算值與參考值的偏差對像點坐標的最大影響值均在1個像素左右，能滿足小像幅圖像解算及糾正的精度要求。同時根據(6)式可以反推出像點坐標偏差值在1個像素時影像畸變參數的允許偏差值△k1：

(2)室內試驗場中，利用三維控制計算結果與直線目標方法計算結果比較接近，影像畸變偏差值對像點坐標的計算和糾正影響可忽略。

(3)影像上直線目標上點的平面坐標是通過手工在軟件上量取的，使得像點坐標存在一些隨機的人為誤差，室內直線目標上點的空間坐標是根據方格網直接量測的，室外直線目標上點的空間坐標是通過精密全站儀測得，也存在一些目標照準的誤差，會造成兩次計算結果的差異，從上述試驗結果看，室外試驗結果比室內試驗結果更趨近于三維鑒定場的參考值。

5 結 語

通過提取影像上多個直線目標，恢復其曲線構像為直線的過程來計算影像畸變，實例計算結果表明該方法可行，選取的直線目標要盡量避免通過像片中心，且盡可能精確測量選取直線目標上點的坐標，直線目標應盡可能均勻分布在影像的各個位置；試驗表明該方法能滿足小像幅圖像解算的精度要求，適用于歷史影像及未知來源的近景影像解算和糾正。

[1] 馮文灝. 非地形攝影測量[M]. 北京：測繪出版社，1985.

[2] 馮文灝. 近景攝影測量[M]. 武漢：武漢大學出版社，2002.

[3] 馮文灝，商浩亮，侯文廣. 影像的數字畸變模型[J]. 武漢大學學報·信息科學版，2006(2)，99～103.

[4] 張永軍，張祖勛，張劍清. 利用二維DLT及光束法平差進行數字攝像機標定[J]. 武漢大學學報，2002.6.

[5] 周富強，邾繼貴，楊學友等.CCD攝像機快速標定技術[J]. 光學精密工程，2002.2.

[6] 謝文寒，張祖勛. 基于多像滅點的相機定標[J]. 測繪學報，2004(4)，335～340.

[7] 于寧鋒. 數字攝影測量系統中非量測CCD相機標定算法[J]. 遼寧工程技術大學學報，2007，26(2)：190～193.

[8] 邱茂林，馬頌德，李毅. 計算機視覺中攝像機定標綜述[J]. 自動化學報，2000，26(1)：43～55.

[9] 胡亞江，沙月進. 求解普通相機徑向畸變系數的一種簡便方法[J]. 測繪與空間地理信息，2009(5)：182～184.

[10] 王建華，石繁槐，張婧等. 攝影機或照相機幾何畸變的標定方法[P]. 專利號：CN1719477.

[11] 王浩，俞青. 一種鏡頭成像畸變校正的方法[P]. 專利號：CN1525396.

[12] 劉傳才. 圖像理解與計算機視覺(第一版)[M]. 廈門：廈門大學出版社，2002年9月.

[13] 馬頌德，張正友. 計算機視覺——計算理論與算法基礎[M]. 北京：科學出版社，1998.

[14] 雷成，胡占義，吳福朝. 一種新的基于Kruppa方程的攝像機自標定方法[J]. 計算機學報，2003，26(5).

[15]ZhangZY.AFlexibleNewTechniqueforCameraCalibration.MicrosoftResearchRedomond.1998.

[16]HeuvelFA.ALine2photogrammetricMathematicalModelfortheReconstructionofPolyhedralObjects.SPIE，1999 ，3641 ：60～70.

Image Distortion Calculation Based on Multi-line Targets Condition

Hu Yajiang1，Sha Yuejin2

(1.Shenzhen Zhongming Survey Engineering Co.，Ltd，Shenzhen 518172，China；2.Southeast University Transportation College，Nanjing 210096，China)

For the unknown sources or unknown camera close range images，the distortion is calculated by extracting the multiple linear targets in the image，and recovering the curve conformation as a straight line. Firstly，analyze the types of image distortion，determine the image distortion model，and then calculate the distortion of multiple linear objects by applying dichotomy method. Through examples calculating of indoor and outdoor test sites，the image distortion parameters calculated by this method are almost same to the results calculated by the three-dimensional calibration field. The experiments results show the method is feasible and can satisfy small image solution precision requirements，suitable for historical images and unknown source images calculation and correction.

image distortion；multiple linear targets；multi-source images；curve conformation；dichotomy

1672-8262(2016)06-70-06

P234.1

B

2016—04—27

胡亞江(1980—)，男，碩士，高級工程師，主要從事攝影測量與地理信息工程的研發工作。