基于間接姿態(tài)估計的初始對準(zhǔn)方法研究*

薛博陽 常路賓 覃方君

(海軍工程大學(xué)導(dǎo)航工程系 武漢 430000)

基于間接姿態(tài)估計的初始對準(zhǔn)方法研究*

薛博陽 常路賓 覃方君

(海軍工程大學(xué)導(dǎo)航工程系 武漢 430000)

姿態(tài)估計初始對準(zhǔn)方法在姿態(tài)確定初始對準(zhǔn)方法基礎(chǔ)之上發(fā)展而來,其在保證姿態(tài)確定對準(zhǔn)算法快速性、抗干擾性的基礎(chǔ)之上,實現(xiàn)了對陀螺漂移的在線建模估計,因此特別適用于低精度捷聯(lián)慣導(dǎo)系統(tǒng)。論文在姿態(tài)估計對準(zhǔn)模型的基礎(chǔ)之上,推導(dǎo)了其對應(yīng)的大失準(zhǔn)角歐拉誤差方程,簡化了濾波算法設(shè)計,車載實驗驗證本文所研究算法的有效性。

姿態(tài)估計; 初始對準(zhǔn); 慣性導(dǎo)航; 誤差方程

(Navigation Engineering Department, Naval University of Engineering, Wuhan 43000)

Class Number V249.1

1 引言

作為一種航位推算系統(tǒng),捷聯(lián)慣導(dǎo)的初始對準(zhǔn)精度和快速性直接關(guān)系到其后續(xù)的導(dǎo)航解算精度及系統(tǒng)機(jī)動性能,因此初始對準(zhǔn)一直是捷聯(lián)慣導(dǎo)技術(shù)領(lǐng)域研究的重點和難點。傳統(tǒng)的初始對準(zhǔn)方法一般包括粗對準(zhǔn)和精對準(zhǔn)兩個過程。粗對準(zhǔn)利用捷聯(lián)慣導(dǎo)自身慣性器件輸出與地球自轉(zhuǎn)角速度和重力加速度之間的關(guān)系直接解析求解出載體姿態(tài)。精對準(zhǔn)一般采用基于卡爾曼濾波的最優(yōu)估計方法完成,因此需要粗對準(zhǔn)提供較為精確的姿態(tài)信息以滿足其濾波模型的線性化條件。然而對于基于MEMS的低精度捷聯(lián)慣導(dǎo)系統(tǒng),由于其慣性敏感器件的常值漂移一般是幾度甚至幾十度每小時,在這種條件下,作為解析粗對準(zhǔn)必要條件之一的地球自轉(zhuǎn)角速度(15deg/h)被完全湮沒在陀螺常值漂移中。因此對于低精度捷聯(lián)慣導(dǎo)而言,即使在靜基座條件下也無法實現(xiàn)有效的解析粗對準(zhǔn)。

為了克服外界干擾對解析粗對準(zhǔn)的干擾,近年來一些學(xué)者提出了一種以慣性系為參考基準(zhǔn)進(jìn)行動基座初始對準(zhǔn)的優(yōu)化對準(zhǔn)新方法[1～6]。該方法通過坐標(biāo)系分解,將初始對準(zhǔn)的核心問題轉(zhuǎn)為求解對準(zhǔn)初始時刻常值姿態(tài)矩陣的問題。優(yōu)化對準(zhǔn)將初始對準(zhǔn)問題轉(zhuǎn)化為利用矢量觀測進(jìn)行姿態(tài)確定的問題,建立了這兩個平行研究數(shù)十年問題之間的聯(lián)系,并將姿態(tài)確定問題中一些成熟算法引入到初始時刻常值姿態(tài)矩陣的求解中。不可否認(rèn),基于姿態(tài)確定的優(yōu)化對準(zhǔn)方法能夠有效處理外界運動干擾,在中高精度捷聯(lián)慣導(dǎo)(如激光和光纖捷聯(lián)慣導(dǎo))中已得到廣泛的實際應(yīng)用和推廣。同時,這種方法能夠?qū)ν鉁y輔助信息反復(fù)利用,極大的提高了初始對準(zhǔn)的速度。然而,基于姿態(tài)確定的初始對準(zhǔn)方法未對慣性器件誤差進(jìn)行建模,因此其本質(zhì)上仍然是一種解析粗對準(zhǔn)方法。正如前文所述,造成傳統(tǒng)初始對準(zhǔn)方法不能正常完成的一個原因是慣性器件性能較差。因此不難推測,基于姿態(tài)確定的優(yōu)化對準(zhǔn)對準(zhǔn)方法因其不能估計除姿態(tài)以外的任何量而不再適用于基于MEMS低精度捷聯(lián)慣導(dǎo)系統(tǒng)。

為了將慣性系初始對準(zhǔn)方法擴(kuò)展到低精度系統(tǒng)中,常路賓提出了一種基于姿態(tài)估計的初始對準(zhǔn)方法。該方法借鑒嚴(yán)恭敏和武元新等人對準(zhǔn)方法中的姿態(tài)矩陣分解的思想[7～8],將姿態(tài)矩陣分解為兩部分,一部分是含有初始誤差的載體姿態(tài)變化矩陣,另一部分是可以借助外界輔助信息進(jìn)行求解的導(dǎo)航系姿態(tài)變化情況。這種姿態(tài)矩陣分解方式的最大好處就是可以實現(xiàn)對陀螺漂移的建模估計,因此特別適用于低精度捷聯(lián)慣導(dǎo)系統(tǒng)的初始對準(zhǔn)[9]。車載實驗表明,常路賓的方法在估計姿態(tài)的同時實現(xiàn)了對陀螺漂移的估計,取得了滿意的效果。

基于姿態(tài)估計的初始對準(zhǔn)方法是針對MEMS低精度捷聯(lián)慣導(dǎo)系統(tǒng)設(shè)計的[ 10],但是該方法直接利用姿態(tài)解算方程作為濾波的狀態(tài)方程,因此計算量很大,對低精度系統(tǒng)而言,不利于其實時應(yīng)用。針對該問題,本文在姿態(tài)估計初始對準(zhǔn)方法的基礎(chǔ)之上,推導(dǎo)了其對應(yīng)的誤差方程,并設(shè)計相應(yīng)的濾波算法,實驗結(jié)果表明,該方法在保證姿態(tài)估計初始對準(zhǔn)方法優(yōu)勢的基礎(chǔ)之上,顯著降低了算法計算量,從而為其實時應(yīng)用提供了有利保證。

2 基于姿態(tài)估計的初始對準(zhǔn)模型

狀態(tài)模型為

(1)

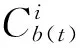
用于修正的觀測方程為

(2)

其中

(3)

(4)

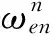
(5)

(6)

微分方程在求解時的初始為:

(7)

3 間接姿態(tài)估計初始對準(zhǔn)方法

由于各種誤差源的影響,實際上捷聯(lián)慣導(dǎo)的模擬的慣性坐標(biāo)系與理想慣性坐標(biāo)系之間存在轉(zhuǎn)動誤差,記實際的慣性坐標(biāo)系為i′系,系先后經(jīng)過三次轉(zhuǎn)動可得i系,假設(shè)三次轉(zhuǎn)動角為ax、ay、az,稱它們?yōu)闅W拉誤差角,并且有a=[ax、ay、az],則坐標(biāo)變換矩陣為

(8)

其中cα=cos(α),sα=sin(α)。將上式中三個矩陣逆序相乘得系i到i′系的變換矩陣。

(9)

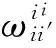
(10)

從而得到歐拉誤差角微分方程

(11)

其中有

(12)

式(11)歐拉誤差角微分方程描述了歐拉角與載體運動間的關(guān)系,建立以歐拉誤差角a表示的捷聯(lián)慣性系誤差模型。

3.1 慣性系姿態(tài)誤差方程

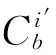
(13)

(14)

現(xiàn)在定義姿態(tài)矩陣的加性計算誤差為

(15)

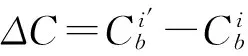
(16)

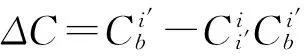
(17)

式(16)和(17)相等,得到:

(18)

(19)

(20)

(21)

3.2 基于姿態(tài)誤差的矢量觀測方程

上一小節(jié)推導(dǎo)了姿態(tài)估計初始對準(zhǔn)的誤差方程形式,為了完成濾波,仍需要推導(dǎo)對應(yīng)的觀測方程。這里將式(2)的矢量觀測方程重寫如下

(22)

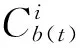
(23)

(24)

上式即為含有姿態(tài)誤差狀態(tài)量的觀測方程。

3.3 濾波器設(shè)計

基于誤差方程的姿態(tài)估計初始對準(zhǔn)算法示意圖如圖1所示。

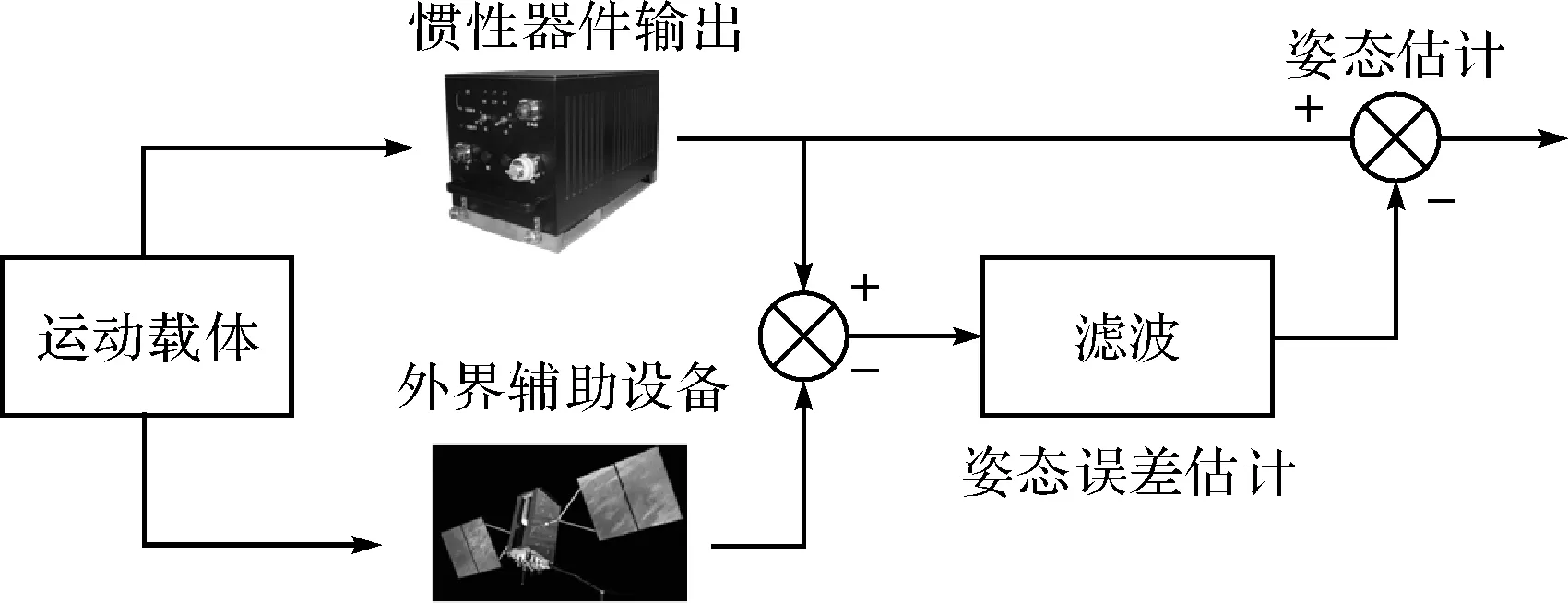
圖1 基于誤差方程的姿態(tài)估計初始對準(zhǔn)算法示意圖

這種形式的濾波本質(zhì)上是一種閉環(huán)濾波,其基本流程是:首先任意給定一個初始姿態(tài)信息,然后根據(jù)陀螺的輸出進(jìn)行姿態(tài)解算,由于初始姿態(tài)中不可避免含有誤差,遞推求解的每個時刻的姿態(tài)也必然存在誤差；同時,根據(jù)構(gòu)造的矢量觀測同樣可以求解一個姿態(tài)解算值,利用這兩種姿態(tài)解算結(jié)果的差值即可進(jìn)行濾波,從而得到姿態(tài)解算的誤差；通過對該姿態(tài)誤差的補(bǔ)償即可獲得姿態(tài)估計信息。

4 車載實驗研究

為了驗證本章所研究算法的有效性,設(shè)計了基于MEMS慣性測量單元的低精度捷聯(lián)慣導(dǎo)車載實驗。車載導(dǎo)航設(shè)備主要包括低精度MEMS慣性測量單元XW-IMU5220和姿態(tài)航向參考系統(tǒng)(attitude and heading reference system,AHRS)XW-ADU7612。其中XW-ADU7612是一個由三個高精度閉環(huán)光纖陀螺儀、三個硅加速度計和兩個GPS天線(XW-ADU3601)構(gòu)成的組合系統(tǒng),用來提供車載實驗所需的高精度姿態(tài)、速度和位置參考。

進(jìn)行對比試驗的算法分別有:文獻(xiàn)[9]中的算法,記為USQUE(濾波算法的縮寫)；本文所提出的算法UKF(針對非線性模型,本文采用的UKF濾波算法)。實驗中我們發(fā)現(xiàn)間接濾波對準(zhǔn)算法對于特別大的失準(zhǔn)角(航向角誤差大于100°)效果不是很理想,因此實驗中增加一種混合算法,即前5s時間內(nèi)使用傳統(tǒng)算法USQUE,后續(xù)時間內(nèi)采用間接濾波方法UKF,該方法記為USQUE+UKF。具體試驗結(jié)果如下所示。

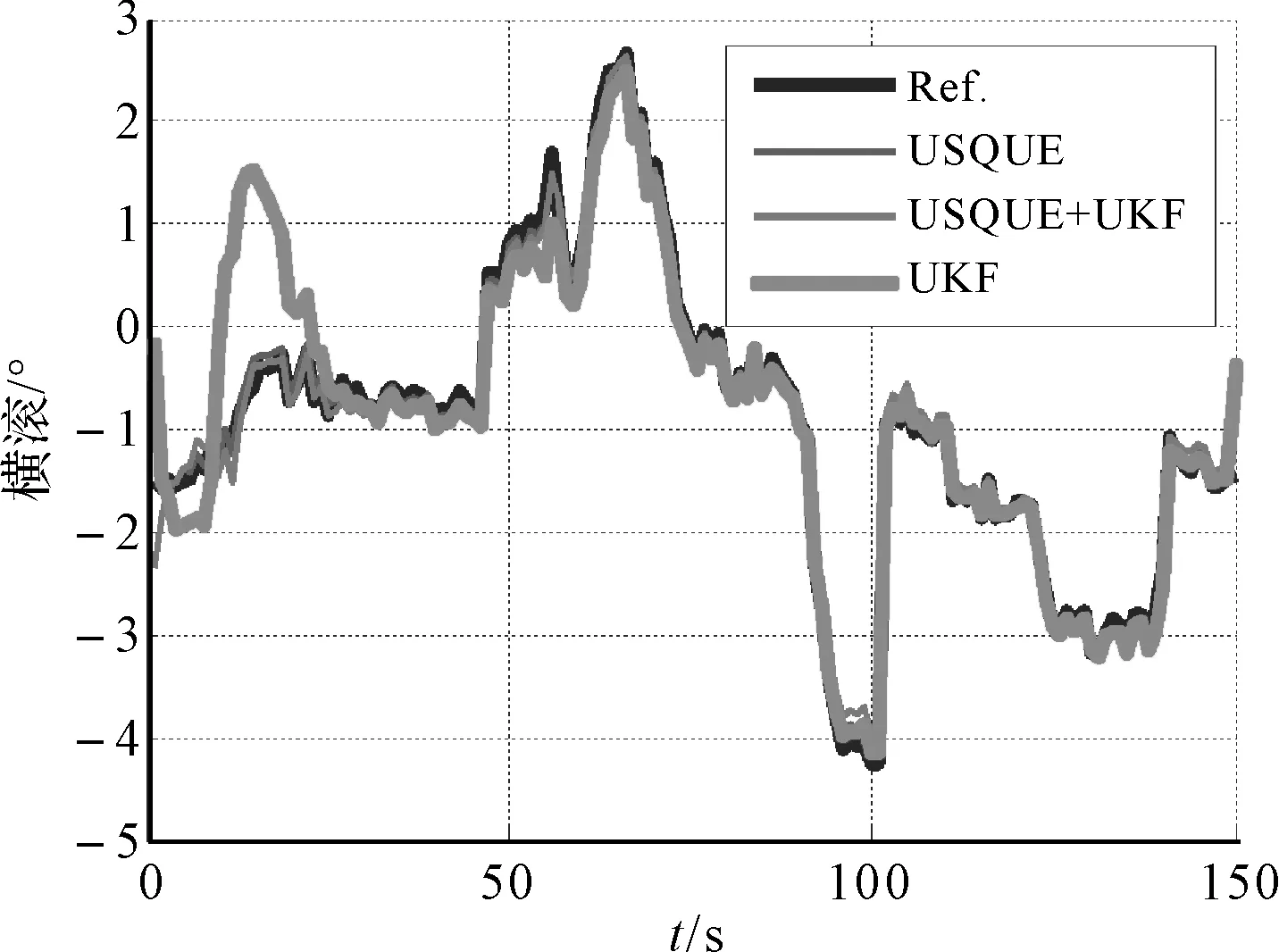
圖2 不同算法下的橫滾角估計值

圖3 不同算法下的橫滾角誤差估計值

圖4 不同算法下的縱搖角估計值

圖5 不同算法下的縱搖角誤差估計值

從圖2～7可以看出,整體來看,在較長時間下直接姿態(tài)估計算法和間接姿態(tài)估計算法都能估計出姿態(tài)角,且估計效果與真實參考數(shù)據(jù)較為一致,達(dá)到了較高的預(yù)期精度要求,但在短時間內(nèi)來看,USQUE算法和混合算法相對來說更加精確,穩(wěn)定性和可靠性都較優(yōu)于UKF算法,并且,通過圖2～7可以看出在整個實驗過程中,各種算法下的姿態(tài)誤差估計值都趨于收斂,相對來看USQUE算法和混合算法的收斂速度要快于UKF算法,UKF算法在個別時間點姿態(tài)估計誤差偏大,且突變型較強(qiáng),穩(wěn)定性差,因此相比來看,USQUE算法和混合算法姿態(tài)估計效果較好。

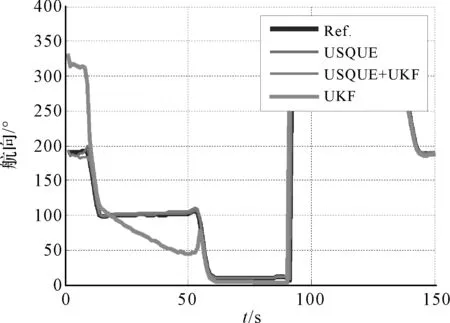
圖6 不同算法下的航向角估計值

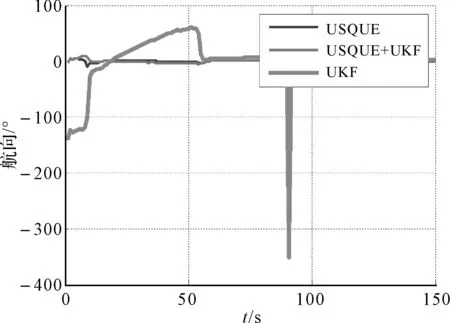
圖7 不同算法下的航向角誤差估計值

同時為了進(jìn)一步分析算法的特點,我們對陀螺偏差進(jìn)行估計,并計算不同算法下的濾波時間,得到不同算法下的濾波時間和不同方向的陀螺偏差估計值如下。

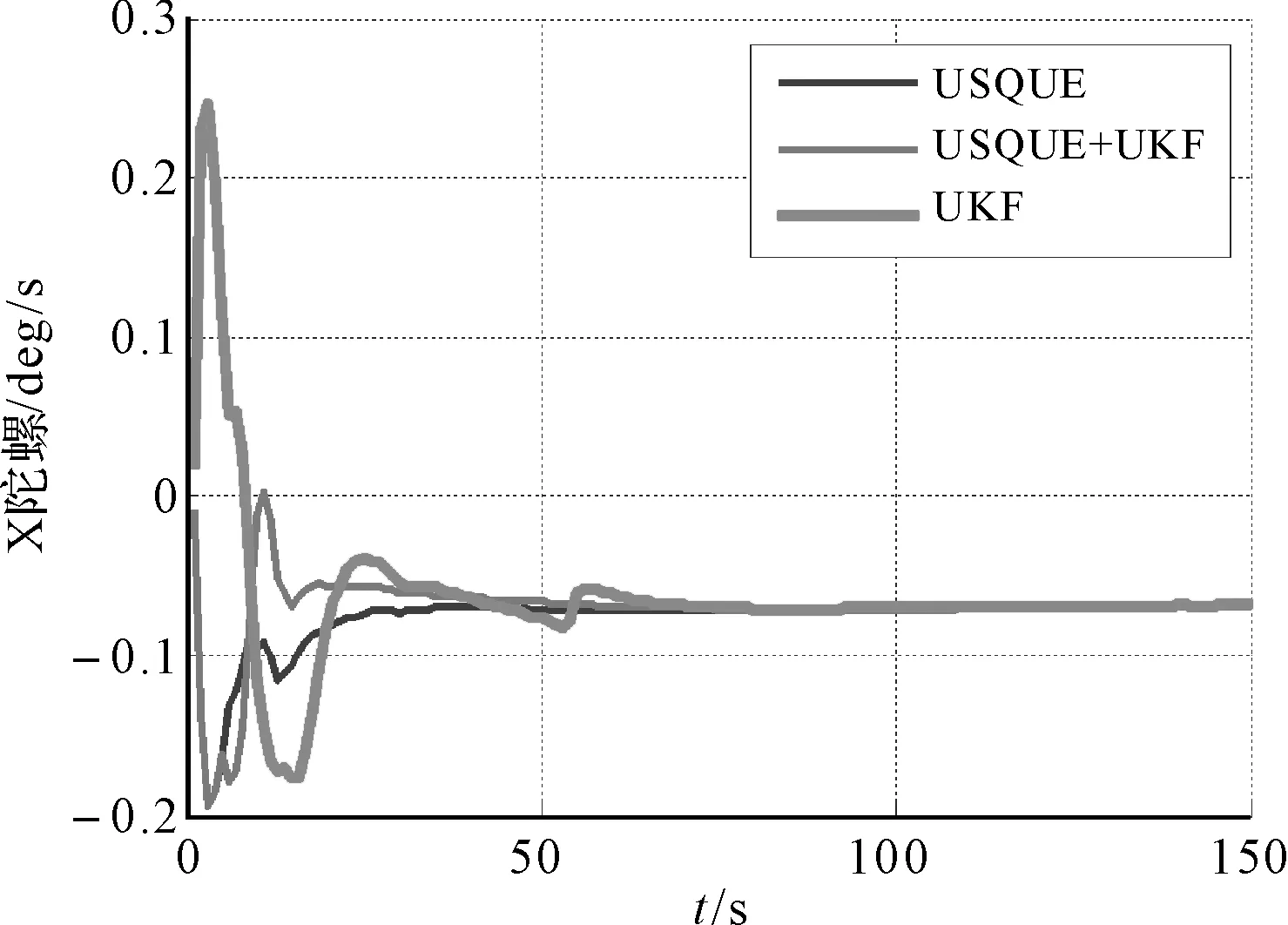
圖8 不同算法下的x-陀螺偏差估計值

由圖8～10可以看出,整體來看,不同方向陀螺偏差估計值都呈收斂的趨勢,且收斂值大致相同,一定程度上驗證了算法的準(zhǔn)確性,同時可以看到,從穩(wěn)定性和精確度來看, USQUE算法最優(yōu),混合算法次之,UKF算法較差,尤其在短時間內(nèi),UKF算法陀螺偏差估計值振蕩較大,同時從圖11中可以直觀的看出三種算法的濾波時間,其中,UKF算法時間最短,USQUE算法濾波時間最長,混合算法時間居中,且與UKF算法時間較為接近,呈現(xiàn)出較好的算法特點。

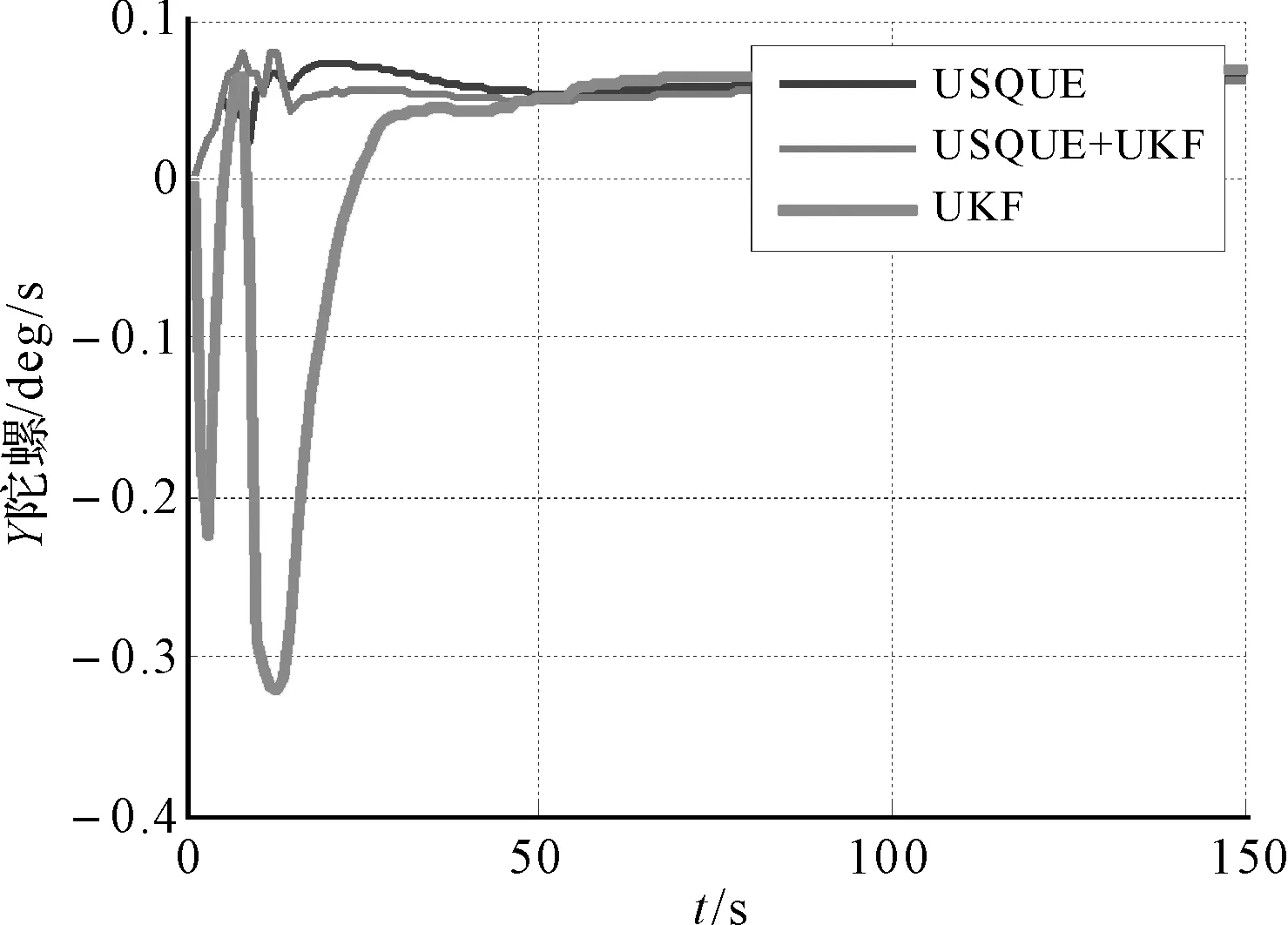
圖9 不同算法下的y-陀螺偏差估計值

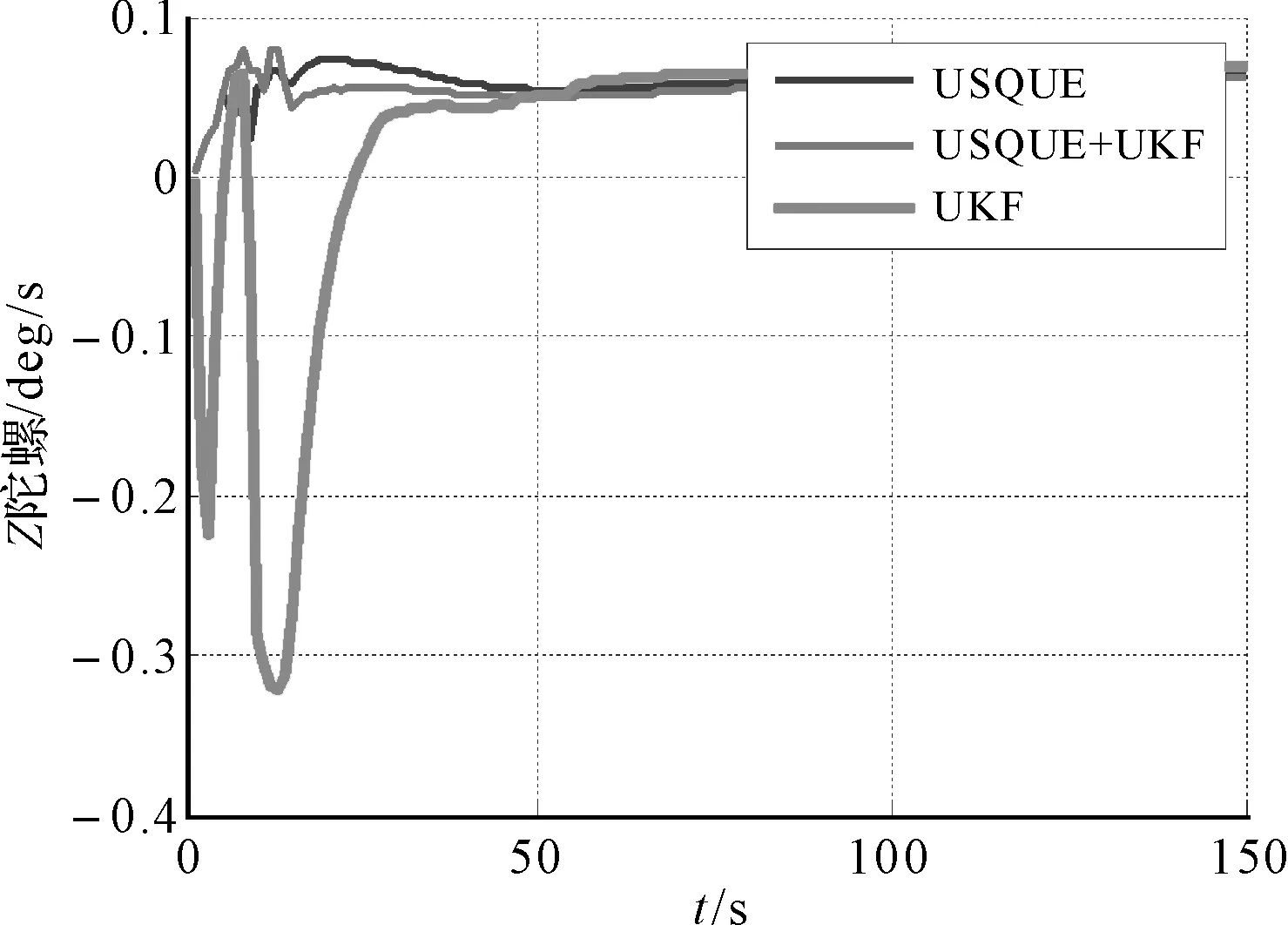
圖10 不同算法下的z-陀螺偏差估計值

圖11 不同算法下的濾波時間

綜上分析,總體來看,本文提出的基于誤差方程的姿態(tài)估計UKF方法在精度和穩(wěn)定性上較上一章的姿態(tài)估計的USQUE算法有明顯不足,但從濾波原理和實驗結(jié)果來看,它能夠有效的縮短濾波時間,簡化運算,在快速性初始對準(zhǔn)方面呈現(xiàn)巨大的優(yōu)勢,并且從本文提出的一種混合算法效果來看,混合算法能夠充分結(jié)合USQUE算法和UKF算法的優(yōu)點,不僅能夠在姿態(tài)估計中保持良好的的精度和穩(wěn)定性,并且在濾波過程中能夠有效減少運算,提高結(jié)算效率。

5 結(jié)語

本文研究了基于姿態(tài)估計的低精度捷聯(lián)慣導(dǎo)初始對準(zhǔn)方法,針對傳統(tǒng)姿態(tài)估計初始對準(zhǔn)方法計算量較大不利于實時應(yīng)用的缺陷,本文在姿態(tài)估計對準(zhǔn)模型基礎(chǔ)之上推導(dǎo)了對應(yīng)的誤差模型并設(shè)計了相應(yīng)的濾波算法。根據(jù)實際應(yīng)用效果,本文進(jìn)一步提出了一種直接和間接姿態(tài)估計的混合初始對準(zhǔn)算法。試驗結(jié)果表明本文所研究算法在保證對準(zhǔn)精度的前提下有效降低了算法計算量,為姿態(tài)估計對準(zhǔn)方法走向?qū)嵱锰峁┝擞行緩健?/p>

[1] Chang L B,Hu B Q,Li A,et al.Transformed unscented Kalman filter [J].IEEE Transactions on Automatic Control,2013,49(2):1400-1402.

[2] 嚴(yán)恭敏,秦永元,衛(wèi)育新,等.一種適用于SINS動基座初始對準(zhǔn)的新算法[J].系統(tǒng)工程與電子技術(shù),2009,31 (3):634-637.

[3] 嚴(yán)恭敏,翁浚,白亮,等.基于慣性參考系的動基座初始對準(zhǔn)與定位導(dǎo)航[J].系統(tǒng)工程與電子技術(shù),2011,33 (3):618-621.

[4] Wu M P,Wu Y X,Hu X P,et al.Optimization-based Alignment for Inertial Navigation Systems:Theory and Algorithm [J].Aerospace Science and Technology,2011,15(1):1-17.

[5] Wu Y X, Zhang H L,Wu M P,et al.Observability of SINS alignment:A global perspective [J].IEEE Transactions on Aerospace and Electronic Systems,2012,48(1):78-102.

[6] Wu Y X,Pan X F.Velocity/position integration formula,Part I:Application to in-flight coarse alignment[J].IEEE Transactions on Aerospace and Electronic Systems,2013,49(2):1006-1023.

[7] Chang L B, Li J S, Li K L. Optimization-based Alignment for Strapdown Inertial Navigation System: Comparison and Extension[J]. IEEE Transactions on Aerospace and Electronic Systems, to be published, 2016. 8.

[8] Chang L B, Li J S, Chen S Y. Initial Alignment by Attitude Estimation for Strapdown Inertial Navigation Systems [J].IEEE Transactions on Instrumentation and Measurement, 2015, 64 (3): 784-794.

[9] 李楊,胡柏青,覃方君,馮國利.MEMS陀螺的抗野值自適應(yīng)濾波降噪方法[J].壓電與聲光,2015,37(4):590-594.

[10] 蘇瑞祥.船用慣性導(dǎo)航設(shè)備虛擬檢測系統(tǒng)設(shè)計與實現(xiàn)[J].系統(tǒng)實踐,2013(7):40.

Initial Alignment Research Based on Attitude Estimation Indirectly

XUE Boyang CHANG Lubin QIN Fangjun

The attitude estimation based initial alignment developed from the attitude determination based initial alignment. Based on insuring the rapidity and anti-interference of attitude determination based initial alignment, it achieved the online modeling estimation for gyroscope drift, which makes it suitable for low-accuracy SINS. Based on the attitude determination based initial alignment, this paper deducted the corresponding large misalignment angle euler error equation and simplified the design of filtering algorithm. And vehicle tests have verified the efficiency of algorithm researched in this paper.

attitude estimation, initial alignment, inertial navigation, error equation

2016年6月10日,

2016年7月30日

薛博陽,男,碩士,研究方向:慣性導(dǎo)航及其應(yīng)用。常路賓,男,博士,講師,研究方向:慣性導(dǎo)航及其應(yīng)用。覃方君,男,博士,副教授,研究方向:慣性導(dǎo)航及其應(yīng)用。

V249.1

10.3969/j.issn.1672-9730.2016.12.016