L1空間上的一個新拓撲

李曉燕

(上海電機學院 數理教學部，上海 201306)

L1空間上的一個新拓撲

李曉燕

(上海電機學院 數理教學部，上海 201306)

Zariski拓撲是代數簇研究中使用的一種拓撲。利用傅里葉分析以及算子代數的理論和方法，構造了L1空間上的Zariski拓撲結構。

L1空間； Zariski拓撲； Fourier變換； Banach代數； 理想

1939年，Zariski對代數曲面奇點解消給出了純代數證明；1944年，他證明特征為0的域上三維代數簇的奇點可解消；1940年他證明了代數簇的局部單值化的存在定理，并引入了Zariski拓撲，使得代數簇成為具有Zariski拓撲的拓撲空間，從而為代數幾何引入了日后起重要作用的上同調理論鋪平了道路。近年來，Zariski拓撲得到了廣泛研究[1-4]，并得到一些有意義的結果。本文給出L1空間上的Zariski拓撲結構。

1 Zariski拓撲

首先引入Zariski拓撲的定義及性質[5-8]，用K表示一個代數閉域，將域K上的仿射空間記作An(K)。

定義1稱V(S)是一個代數子集，若它是K[z1,z2,…,zn](n∈N)中多項式的集合S的零點集,即

V(S)=

(a1,a2,…,an)∈An(K)|{f(a1,a2,…,an)=0

?f(z1,z2,…,zn)∈S}, n∈N

顯然，若S?S′，則V(S)?V(S′)。特別地，對于空集?，有V(?)=Kn。

定理1[8]設a是由S生成的理想，則V(S)=V(a)。

定理2[8]可以證明有以下性質：

(1) 若a?b，則V(a)?V(b)，其中，b是由S生成的理想；

(2)V(0)=An(K)，V(K[z1,z2,…,zn])=?，(n∈N);

(3)V(ab)=V(a∩b)=V(a)∪V(b)；

性質(2)～(4)表明，將An(K)作為一個拓撲空間，代數子集滿足閉集的性質：空集和全集都是閉的，對于有限并運算和任意交運算都封閉。將該種拓撲稱為Zariski拓撲。

定義2設任一子集W?An(K)，稱I(W)為W的理想，若

I(W)= {f∈K[z1,z2,…,zn]|f(P)=0, 所有P∈W}

其中,P為仿射空間的一個點，P∈An(K)。可以得到以下性質：

(1) 若V?W，則I(V)?I(W)；

(2)I(?)=K[z1,z2,…,zn]；I(An(K))=0；

(3)I(∪Wi)=∩I(Wi)。

證明

(1) 對任意P∈V，由于V?W，故P∈W；取任意f∈I(W)，則f(P)=0，從而f∈I(V)，即證明了I(V)?I(W)。

(2) 該結論顯然成立。

(3) 對任意f∈I(∪Wi)，取任意P∈Wi，有P∈∪Wi，則f(P)=0，從而f∈I(Wi)；進一步有

f∈∩I(Wi)，I(∪Wi)?∩I(Wi)

另一方面，對任意f∈∩I(Wi)，取任意P∈Wi，都有P∈∪Wi，且有f(P)=0，于是

f∈I(∪Wi)，I(∪Wi)?∩I(Wi)

結論得證。

定理3[8]對任一子集W?An(K)，V(I(W))是An(K)中包含W的最小代數子集。特別地，W為代數子集時，V(I(W))=W。

2 Fourier變換的L1基本理論

這里介紹Fourier變換的基本性質[9-12]。先引入記號，用En表示n維歐氏空間。本文主要討論定義在En上的函數空間L1。

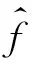
(1)

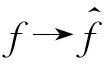
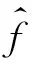
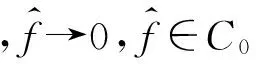
定義4函數f,g∈L1(En)，稱h為f、g的卷積，若

則h=f*g。

定理6若f∈Lp(En)，1≤p≤∞，且g∈L1(En)，則h∈Lp(En)，且‖h‖p≤‖f‖p‖g‖1。

設τh和δa分別為平移算子和伸縮算子。若f,g∈L1，則Fourier變換有如下結果：

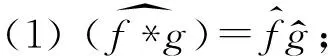
現討論Fourier反演問題，即給定一個函數的Fourier變換，如何得到原函數？

定理7設f,g∈L1，有

(2)

可由Fubini定理[9]證明之。

若f,φ∈L1，δε為伸縮算子，對f(x)和 e2πixδεφ(x) 運用上述定理和Fourier變換平移算子的計算公式可得到定理8和定理9。

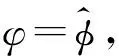
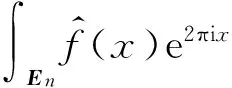
(3)

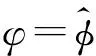
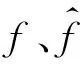
(4)

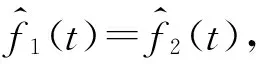
3 Banach代數[13-14]

定義4一個復代數是復數域C上的向量空間A，其中A上定義有乘法，對于所有x,y,z∈A和所有標量α，滿足：

(1)x(yz)=(xy)z；

(2) (x+y)z=xz+yz,

x(y+z)=xy+xz；

(3) α(xy)=(αx)y=x(αy)；

若A是Banach空間，其范數滿足乘法不等式:

(4) ‖xy‖≤‖x‖·‖y‖,x,y∈A

并且A包含單位元e，使得

(5)xe=ex=x,x∈A，‖e‖=1

則稱A為Banach代數。

定理10假定A是Banach空間具有單位元e≠0的復代數，其中乘法是左連續和右連續的，則A上存在范數，它導出與所給拓撲相同的拓撲，且使A成為Banach代數。

顯然，x→Mx是線性的，結合律意味著Mxy=MxMy。若x∈A，則

‖x‖=‖x e‖=‖Mxe‖≤

‖Mx‖·‖e‖

(5)

‖MxMy‖≤‖Mx‖‖My‖

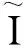
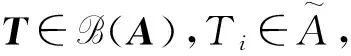
Ti(y)=xiy=(xie)y=Ti(e)y

(6)

當i→∞時，式(10)中Ti(y)趨于T(y),而Ti(e)→T(e)。由于A中乘法做連續，故式(10)中最后一項Ti(e)y為T(e)y。令T(e)y=x，則

T(y)=T(e)y=xy=Mxy

特別地，L1(En)以卷積為乘法，是個交換 Banach 代數。

定義5子集J是復交換代數A的子空間，且對任何x∈A和y∈J，有xy∈J，則A的子集J為一個理想。

若J≠A,J是真理想。顯然可以得到定理11、12。

定理11A的真理想不包括A的任何可逆元；理想的閉包也是理想。

定理12若A是具有單位元的交換復代數，則A的每個真理想都包含在一個極大理想之中。若A是交換Banach代數，則A的每個極大理想是閉的。

4 L1空間上的Zariski拓撲

現將Zariski拓撲推廣到L1空間上。

定義6設I為L1(En)的閉理想，則稱Z(I)為I的譜點集，ξ為(En)空間中的向量。若

顯然若I1?I2，則Z(I1)?Z(I2)。

引理1[13]若f∈L1(En), 向量t∈En,ε>0,則存在h∈L1(En),‖h‖1<ε,使得對于t的某一鄰域中的所有向量s，有

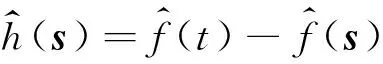
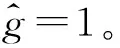
gλ(x)=eitxλ-ng(x/λ)

且定義

有

故當λ→∞時，‖hλ‖1→0。

定理13[13]若函數ω∈L∞(En)，Y是L1(En)的子空間，且對每一個f∈Y，有

f*ω=0

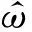
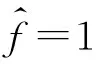
h∈L1(En)，‖h‖1<1

對在v的某一鄰域中的所有s，有

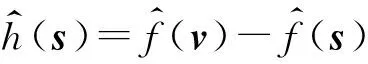
故只需證明ω*ψ=0即可。

令g0=ψ,gm=h*gm-1,m≥1，則

‖gm‖1≤‖h‖m1‖ψ‖1

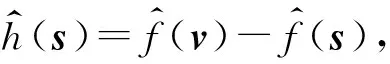
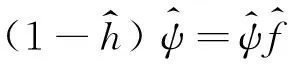
或

故有ψ=G*f，且

ψ*ω=G*ψ=0

定理14Y=L1,當且僅當Z(Y)=?。

證明若Z(Y)=?，則由上文定理易知Y的補空間平凡，故可推出Y=L1。反之顯然。

定理15Y={0},當且僅當Z(Y)=En。

證明若Y={0}，顯然有Z(Y)=En。

若Z(Y)=En，則

由Fourier逆變換的唯一性知f=0，故Y={0}。

定理16

(a)Z(XY)=Z(X∩Y)=Z(X)∪Z(Y)；

證明

(a) 若ξ?Z(X)∪Z(Y)，則存在f∈X,g∈Y，使得

f(ξ)≠0，g(ξ)≠0

故由Fourier逆變換和卷積的Fourier變換的性質知

(f*g)(ξ)≠0

故有ξ?Z(XY)，從而有

Z(XY)?Z(X)∪Z(Y)

由于XY?X∩Y?X,Y，故有

Z(XY)?Z(X∩Y)?Z(X)∪Z(Y)

因此,結論(a)成立。

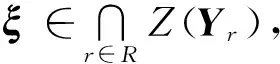
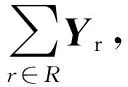
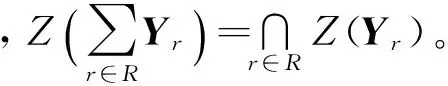
綜上所述表明，譜點集有閉集的性質，故L1上也具有Zariski拓撲。

定理17I(A)是L1理想，且有A=Z(I(A))。

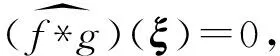
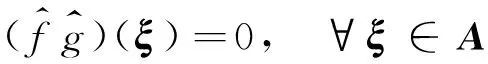
因此，I(A)是L1理想。顯然A=Z(I(A))。

[1] ABUHLAIL J Y. A Zariski topology for bicomodules and corings[J]. Applied Categorical Structures，2007，16(1/2)：13-28.

[2] ABUHLAIL J. Zariski topologies for coprime and second submodules[J]. Algebra Colloquium，2015，22(1)：47-72.

[3] DARANI A Y，MOTMAEN S. Zariski topology on the spectrum of graded classical prime submodules[J]. Applied General Topology，2013，14(2)：159-169.

[4] ANSARI-TOROGHY H，FARSHADIFAR F. The Zariski topology on the second spectrum of a module(Ⅱ)[J]. Bulletin of the Malaysian Mathematical Science Society，2016，39(3)：1089-1103.

[5] SHAFAREVICH I R. Basic Algebraic Geometry 2.[M]. Reid M,譯.[S.I.]:Spring,1998：3-14.

[6] Harris J. Algebraic Geometry.[M].[S.l.]:世界圖書出版公司，2000：1-18.

[7] ATIYAH M F，MACDONALD I G. Introduction to Commutative Algebra[M]. Lodon:Addison-Wesleg Publishing Co.,1969:1-16.

[8] KUNZ E. Introduction to commutative algebra and algebraic geometry[M].[S.l.]:Birk?user,Springer，1982：1-21.

[9] 程民德，鄧東皋，龍瑞麟.實分析[M].2版.北京：高等教育出版社，2008：65-134.

[10] STEIN E M，SHAKARCHI R. Fourier Analysis:An Introduction[M]. Princeton, NJ:Princeton University Press 2007：129-207.

[11] STEIN E M,WEISS G.Introduction to Fourier Analysis on Euclidean Space[M]. Princeton, NJ:Princeton University Press，1971：1-40.

[12] STEIN E M. Singular Integrals and Differentiability Properties of Function[M]. Princeton，NJ:Princeton University Press，1970：1-34.

[13] RUDIN W.泛函分析(英文版·第2版)[M].北京.機械工業出版社，2003:182-201.

[14] LAX PD.泛函分析(影印版)[M].北京.高等教育出版社，2007：192-202.

A New Topology over L1Space

LI Xiaoyan

(Department of Mathematics and Physics, Shanghai Dianji University, Shanghai 201306, China)

Zariski topology is used in algebraic varieties studies. Using Fourier analysis and operator algebra, we construct a Zariski topological structure on the L1 space.

L1space; Zariski topology; Fourier transform; Banach algebra; ideal

2016-10-05

上海高校青年教師培養計劃資助(A1-5701-15-011-09);上海電機學院重點學科項目資助(16JCXK02)

李曉燕(1985-)，女，講師，博士，主要研究方向為偏微分方程及數學物理，E-mail：lixy@sdju.edu.cn

2095-0020(2016)06-0364-05

O 177

A