液位控制系統干預下小孔全過程泄漏速率模型

付建民，張伯倫,2，陳國明，鄭曉云，葉闖，郭超，朱淵

（1中國石油大學（華東）海洋油氣裝備與安全技術研究中心，山東 青島 266580；2大連港股份有限公司，遼寧 大連 116600）

液位控制系統干預下小孔全過程泄漏速率模型

付建民1，張伯倫1,2，陳國明1，鄭曉云1，葉闖1，郭超1，朱淵1

（1中國石油大學（華東）海洋油氣裝備與安全技術研究中心，山東 青島 266580；2大連港股份有限公司，遼寧 大連 116600）

泄漏速率是計算泄漏量、確定泄漏持續時間及評估泄漏風險的前提和基礎，通過搭建液相儲罐小孔泄漏實驗系統，構建不同泄漏場景，對比液位控制系統干預下的泄漏速率變化情況，并結合泄漏速率模型計算值進行分析。結果表明：液位控制系統響應后，泄漏速率下降速度變緩，并隨時間推移逐漸開始回升，最后穩定在某值處達到穩態泄漏，進出流量對儲罐小孔泄漏速率的影響基本可忽略。通過改進儲罐泄漏經典公式，建立基于實際液位控制系統干預條件下的儲罐小孔泄漏速率模型，提出泄漏孔口高壓修正系數計算方法和模型，通過驗證分析證明該模型可有效提高液位控制系統干預下泄漏速率計算精度。

液位控制；泄漏速率；模型；實驗驗證；安全

引 言

隨著石油化工行業的飛速發展，由危險性液體儲罐泄漏而引發的火災爆炸事故仍然時有發生。不論是泄漏事故發生過程中選取合理的應急措施，還是泄漏事故發生后的后果評估都需要快速準確地計算泄漏強度。特別是在計算儲罐泄漏后果時，需要輸入準確的泄漏速率，否則對風險計算結果有非常顯著的影響。在泄漏風險評估方面，《SY/T 6714—2008基于風險檢驗的基礎方法》中采用的RBI（基于風險檢驗）方法對事故后果進行評估過程中，確定泄漏孔尺寸后就需要計算泄漏速率，并估算泄漏流體總量[1]。由此可見，泄漏速率計算是后果評估過程中非常重要的一環，只有準確確定泄漏速率，才能使風險計算結果更加精確。

Woodward等[2]在 1991年首次提出了儲罐發生小孔泄漏時泄漏強度的計算問題，他們將流體視為“理想流體”，但沒有提出完整的儲罐小孔泄漏計算模型；Crowl[3]在Woodward等的基礎上，對特定形狀的容器以及泄漏發生在容器底部的情況進行分析，提出了對應儲罐泄漏模型；Kordestani等[4]利用橢圓積分法提出臥式圓柱形儲罐任意位置的量綱1泄漏時間模型，考慮儲罐中壓力變化影響對液體從唯一孔洞中泄漏進行了擴展研究；Hart等[5]提出了一種球罐表面任意高度小孔的量綱1泄漏時間及平均泄漏速率模型；Lee等[6]提出了不同幾何形狀的容器在任意高度泄漏的泄漏時間以及平均泄漏速率大小；Fthenakis等[7]提出的一種簡單、精確的模型來確定氣液兩相從壓力儲罐泄漏的泄漏量和組分，該模型是基于氣液兩相界面之間的動量轉移的方程，適用于液位之上的一個較大裂口發生泄漏；Beck等[8]提出低壓條件下，通過狹窄裂縫泄漏的泄漏速率計算模型；Cassa等[9]分析得出泄漏孔處壓力與泄漏孔直徑或裂縫長度呈指數關系，并提出了泄漏速率與壓力水頭的函數關系；Xie[10]研究不同特征裂縫對泄漏影響情況，特別針對多重裂縫變化情況進行了研究；Yang等[11]通過實驗研究分析壓降對泄漏速率變化的影響，總結了均勻非平衡模型和摩擦阻力模型的適用范圍；Woodward[12]對比了能量守恒模型和非平衡模型的實驗數據，并改進了原始均衡泄漏模型；Luo等[13]提出了危險氣體從高壓管道小孔泄漏的泄漏速率簡化公式，簡化后的公式與復雜公式相比只有7%的誤差，但可以更快速地估算出泄漏速率；Chang等[14]根據測試數據，提出薄管裂縫泄漏速率的計算方法；Lu等[15]通過研究雙殼油船（DHT）底部破裂孔原油泄漏的動態過程，提出破裂DHT的原油泄漏表現和整個工藝過程的動態流動特征。蔣軍成等[16]根據泄漏源位置、形式與特征的不同，將泄漏模型分為密封元件的滲漏模型、儲罐或管道的泄漏模型和泄壓元件的泄放模型3種類型，總結了各種模式下的泄漏強度量化模型；王大慶等[17]通過對現有壓力容器泄漏源模型的研究，對模型的應用計算進行了合理簡化，并結合實例分析總結出在臨界泄漏結束時容器內剩余氣體質量所占比例甚小，從而提出采用臨界泄漏階段的平均泄漏率來近似代替整個泄漏階段的總平均泄漏率，不僅簡化了計算過程，而且在使用于風險后果定量分析時的計算結果保守性較好；劉宗明等[18]通過分析泄漏孔內氣體流動規律和壓力容器內氣體參數狀態特性，并通過實驗研究，建立了反映泄漏孔當量半徑的數學模型，這為進一步研究不同容積壓力容器的泄漏情況、泄漏規律提供了重要參考；王志榮等[19]通過實驗模擬立式圓柱形儲罐的泄漏過程，分析了泄漏量、質量泄漏速率和液面高以及泄漏時間的關系，總結出當量泄漏面積相等時，兩個小孔同時泄漏的泄漏量近似等于單孔泄漏量；任榮亭等[20]建立實際儲罐泄漏實驗模擬系統，研究實際泄漏規律，結果表明，實驗數據與理論計算的泄漏規律大致相同；李金光等[21]基于實際工程設計工作的需要，研究了全容式LNG儲罐內罐泄漏動態過程的特點，建立了描述內罐泄漏動態過程的泄漏源模型，推導了基于泄漏孔位置的泄漏液體液位高度與泄漏持續時間關系的方程。

目前普遍接受的儲罐泄漏模型是根據伯努利方程建立的液相儲罐泄漏經典泄漏公式[22]

式中，Qm為質量流率，kg·s?1；A為泄漏孔口面積，m3；C0為流出系數，根據實際情況取值；ρ為水密度，1000 kg·m?3；p為容器內表壓力，Pa；g為重力常數，9.8 m·s?2；h為液位在泄漏孔之上高度，m。

上述經典泄漏公式中表壓力p代表泄漏發生后儲罐內實時壓力值，h代表液位到泄漏孔的高度。針對儲罐泄漏經典公式，需要確定儲罐發生泄漏時實時壓力以及泄漏孔之上的液位高度，方能計算出泄漏速率。這就需要確定泄漏發生過程中的實時壓力和液位高度，但并不是所有儲罐都可以同時獲取實時壓力和液位高度。另外，經典公式一般適用于封閉儲罐，對于工藝系統中儲罐發生泄漏的情況是否適用并未進行有效說明。所以，儲罐經典泄漏模型適用范圍比較有限。

以上研究主要集中在固定場景的泄漏速率和模型研究，以泄漏達到穩定狀態為主，沒有將泄漏放置在工藝系統背景中進行考慮，本研究在儲罐經典泄漏模型基礎上，結合理想氣體狀態方程，對泄漏經典公式進行改進，研究典型的工藝過程控制系統——液位控制系統干預下的罐泄漏速率計算模型，并結合實驗進行驗證。

1 液位控制系統干預下的儲罐小孔泄漏過程分析

配有液位控制系統的壓力容器在泄漏發生后，液位下降至液位控制觸發點，液位控制系統響應，通過調節，若液位重新回到觸發點以上，液位控制系統停止響應，液位保持穩定。若通過調節，液位仍不斷下降，達到報警值，液位控制系統失效，泄漏ESD緊急關斷。

1.1 液位控制系統動作前泄漏模型

假定泄漏發生后，液位控制系統響應前，此時液位仍屬正常狀態，泄漏未受到控制。根據儲罐泄漏經典公式，泄漏發生后（圖1），p1代表泄漏發生后儲罐內實時壓力值，h1代表液位到泄漏孔的高度。此時泄漏質量流量為

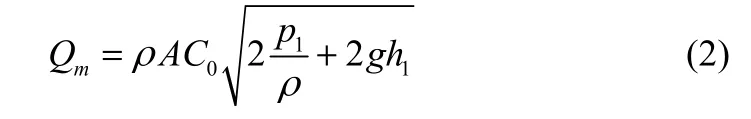
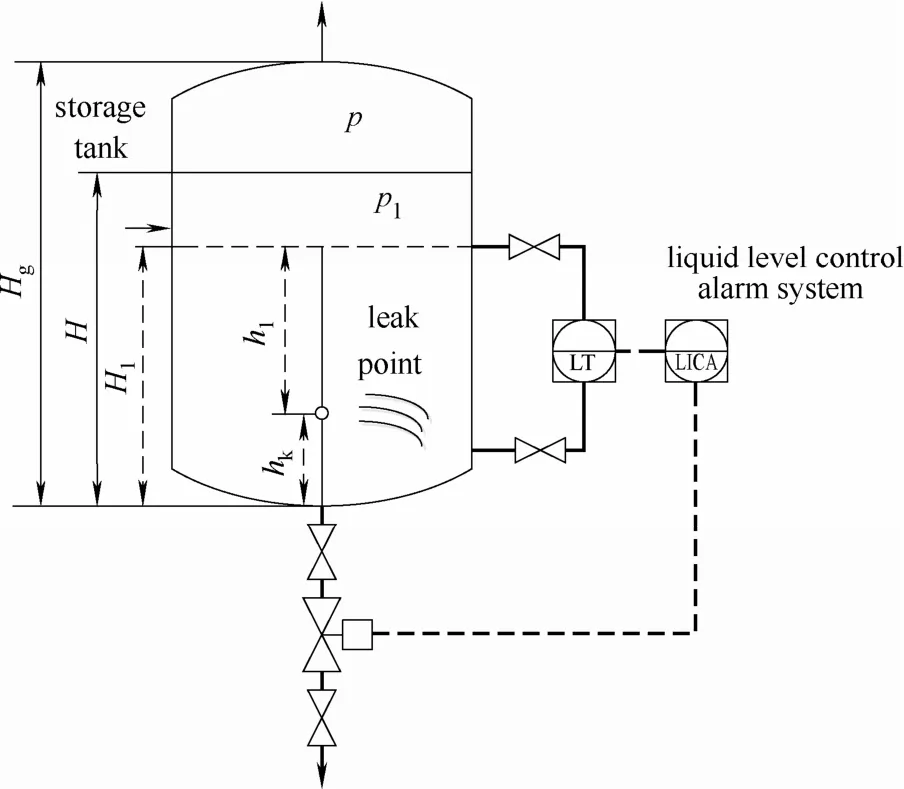
圖1 液位控制干預下儲罐小孔泄漏Fig.1 Tank hole-leakage based on impact of level control system

但是在工藝系統中，并不是所有的壓力容器都會同時配有遠傳的壓力表和液位計。而配有液位控制系統的壓力容器通常均設有遠傳液位變送器，通過實時遠傳液位讀數，即可計算出泄漏速率大小。

假設壓力容器上方氣體為理想氣體，根據理想氣體狀態方程pV=nRT，其中，p為氣體壓力，Pa；V為氣體體積，m3；n為氣體摩爾數，R為摩爾氣體常數，8.314 J·mol·K?1；T為熱力學溫度，K。當泄漏發生時，隨著容器中液位下降，假設液位上方氣體膨脹為絕熱膨脹，氣體溫度不變。由于容器頂部弧形區域較為平滑，假設上方氣體空間為立方體，則 pV=p1V1，考慮到立式圓柱形儲罐橫截面積恒定，所以

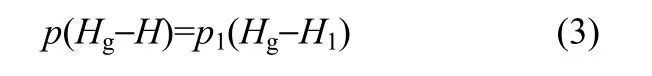
轉換得到

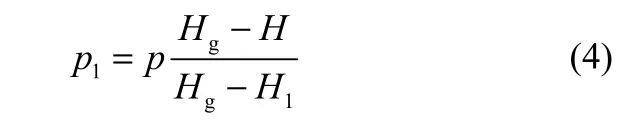
將式(3)代入式(2)中得到

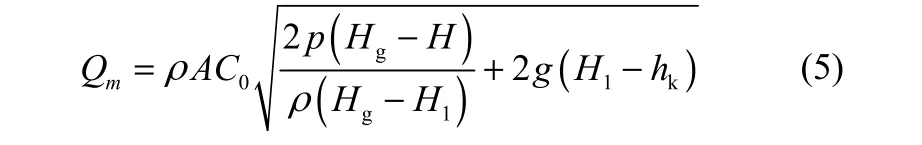
式(5)在液位控制系統響應前，只需要已知容器內泄漏前的初始壓力、初始液位高度以及泄漏發生后的實時液位高度就可計算出泄漏速率。

1.2 液位控制系統動作后泄漏模型

泄漏發生后，液位下降至調節觸發點，液位控制系統響應，液位下降速度變緩。經過一段時間液位停止下降，并逐步開始緩慢回升。此過程液位處于波動階段時，計算實時泄漏質量流量需要已知儲罐實時液位高度。設有液位控制系統的儲罐，可以通過獲取液位調節過程中儲罐內的實時液位值，運用式(5)來計算此階段泄漏速率。

當液位回升至調節觸發點以上時，液位控制系統停止調節，液位上升變緩，最終穩定在觸發點以上某液位 HA處，泄漏轉變成穩態泄漏。此時泄漏速率為

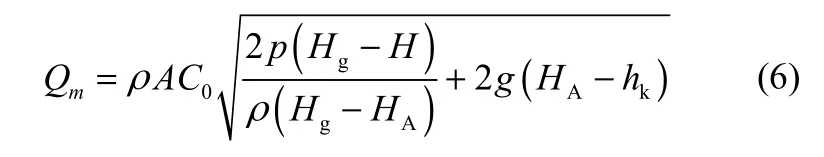
1.3 模型泄漏系數

規則形狀的泄漏孔，孔洞形狀不同，Reynolds數不同，泄漏系數也不同，取值見表1。

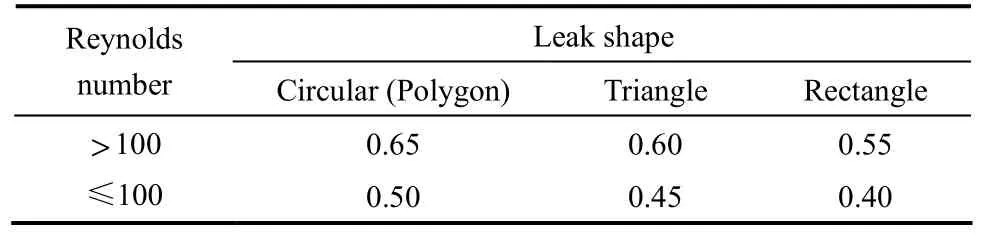
表1 液相泄漏系數C0[23]Table 1 Liquid leakage coefficient C0[23]

本文實驗泄漏孔形狀為圓形，且Reynolds數大于100，故泄漏系數C0取值0.65。

2 液相儲罐泄漏實驗

2.1 實驗系統

利用相似原理搭建液相儲罐小孔泄漏實驗系統。圖2為液相儲罐小孔泄漏實驗系統流程。實驗以液體水為介質。實驗系統主要包括動力單元、測量儀表單元、泄漏模塊以及數據采集單元等。

動力單元包括貯罐、高壓柱塞泵、緩沖罐，為系統提供穩定壓力的液態水。

測量儀表單元包括液位計、流量計以及壓力表，用于監測系統運行中的各項參數。

泄漏模塊是一個內徑500 mm，高度1506 mm的立式圓柱形儲罐，距離容器底部550 mm開有兩個圓形泄漏孔，直徑分別為 5、10 mm，利用球閥控制泄漏發生。

數據采集單元包括PLC控制器和計算機，實現實驗過程中實時參數的采集和處理。

2.2 技術思路

實驗通過氣液混相裝置和儲罐進出口流量調節閥構建不同泄漏場景，保證初始液位恒定，選取不同的初始壓力，研究儲罐經典泄漏公式是否適用于工藝系統中的壓力容器泄漏以及液位控制系統對壓力容器泄漏速率響應關系。

2.3 泄漏場景

重點對液位控制系統作用下的小孔泄漏規律進行研究，根據AQ/T 3046—2013《化工企業定量風險評價導則》，小孔泄漏范圍為0～5mm，5 mm為小孔泄漏尺寸代表值[24]，采用直徑5 mm作為典型小孔泄漏尺寸進行實驗。

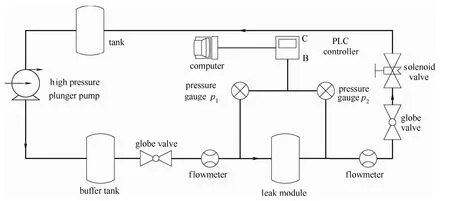
圖2 液相儲罐泄漏實驗系統流程Fig.2 Flow chart of liquid tank leakage experiment system

實驗過程中，水通過柱塞泵增壓進入實驗系統，然后利用氣液混相裝置將空氣和水混合注入泄漏模塊（儲罐）中，調節儲罐進出口流量，通過觀察液位計，保證壓力容器內初始液位達到80 cm，并通過調節壓力控制系統來達到指定初始壓力。實驗所用儲罐為不銹鋼材質，根據管道所能承受壓力范圍以及儀表測量范圍確定初始壓力，分別保證初始壓力高于 0.2、0.4、0.6、0.8、1.0 MPa，進行 5組不同初始壓力的泄漏實驗。保持泵排量恒定，調節出口電磁閥，保證進出口流量一致。

（1）進行無控制壓力容器直徑5 mm小孔泄漏實驗，泄漏發生后液位下降至接近泄漏孔處停止泄漏。

（2）進行液位控制系統干預下的壓力容器直徑5 mm小孔泄漏實驗，泄漏發生后，液位下降，下降至70 cm（報警值）液位控制系統響應，待液位重新穩定后，繼續泄漏一段時間停止泄漏。

依據以上兩種泄漏場景，均保持其他條件不變，改變初始壓力進行多組實驗。

2.4 實驗結果與分析

2.4.1 液位控制系統干預下的儲罐泄漏規律研究

（1）液位控制系統執行前模型適用性分析

圖3～圖7為不同初始壓力液位控制下的小孔泄漏速率曲線，包含液位控制系統作用下泄漏速率實驗值、理論值，及無控制情況下泄漏速率實驗值。在液位控制系統響應前（液位控制觸發點時間之前），對比無控制泄漏速率實驗值和液位控制作用下泄漏速率理論值，可發現二者擬合良好，最大誤差不超過4.5%，故可認為進出流量對儲罐小孔泄漏的影響可以忽略，儲罐泄漏經典公式基本適用于過程工藝系統中的儲罐泄漏情況。

圖3 1.00 MPa液位控制泄漏速率曲線Fig.3 Tank leakage rate of 1.00 MPa with level control system

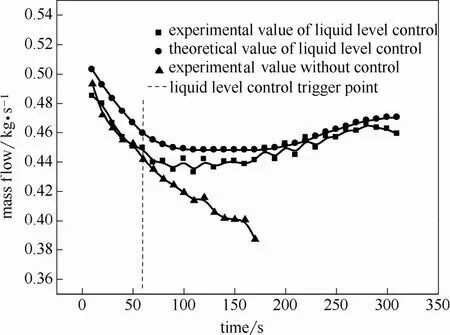
圖4 0.83 MPa液位控制泄漏速率曲線Fig.4 Tank leakage rate of 0.83 MPa with level control system

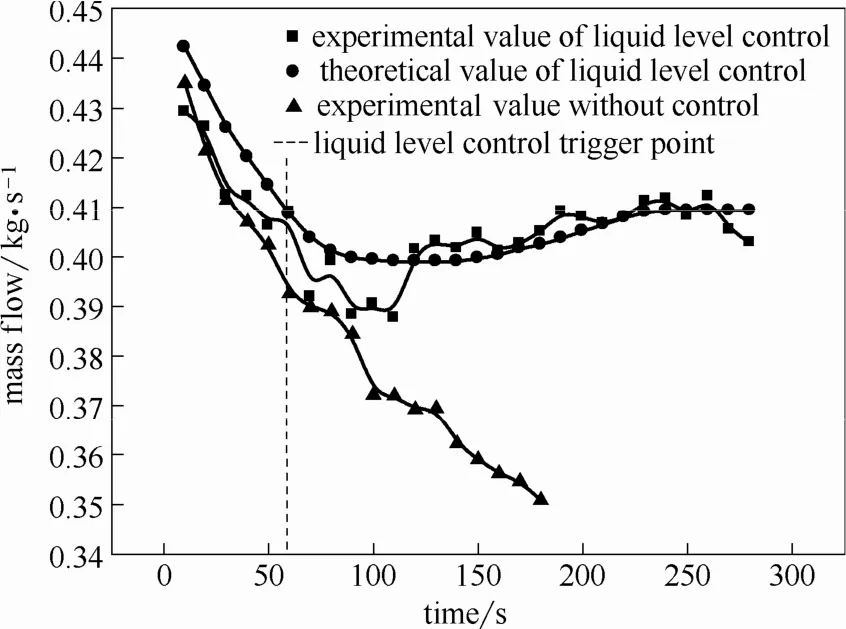
圖5 0.63 MPa液位控制泄漏速率曲線Fig.5 Tank leakage rate of 0.63 MPa with levelcontrol system

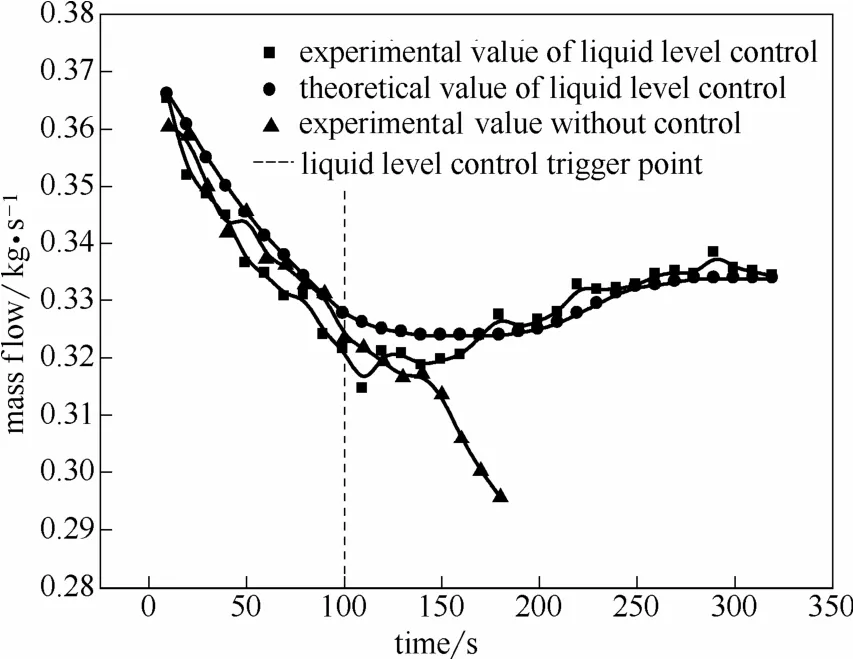
圖6 0.40 MPa液位控制泄漏速率曲線Fig.6 Tank leakage rate of 0.40 MPa with level control system

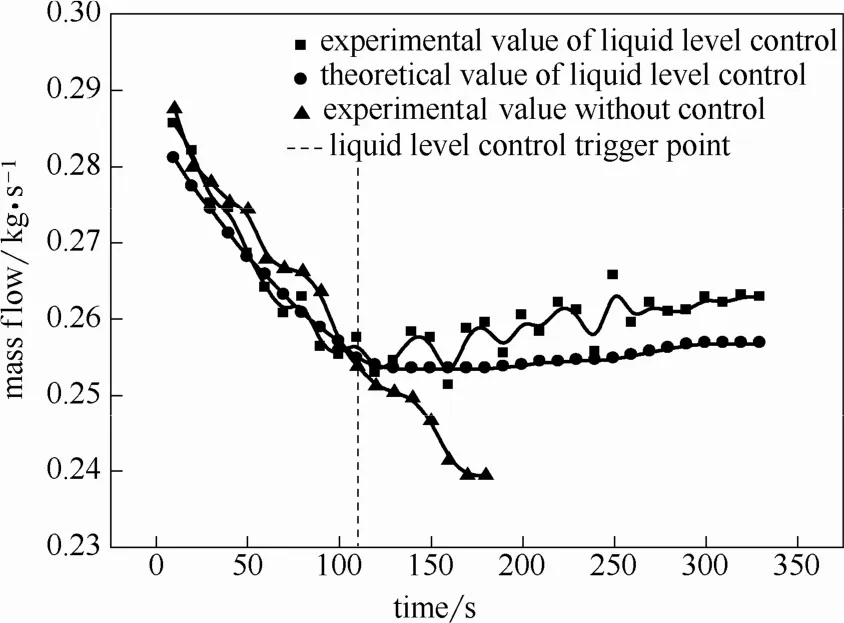
圖7 0.23 MPa液位控制泄漏速率曲線Fig.7 Tank leakage rate of 0.23 MPa with level control system

（2）液位控制系統執行后模型適用性分析

對比無控制泄漏速率實驗值和液位控制作用下泄漏速率實驗值，在無控制情況下，泄漏速率呈線性遞減。而當液位控制系統響應后，泄漏速率下降速度變緩，并隨著時間推移，逐漸開始回升，最后在某點處保持穩定，達到穩態泄漏。因此，液位控制系統響應并不能對泄漏強度起到抑制作用，反而會使泄漏強度增大，造成更加嚴重的事故后果。

泄漏發生后，液位下降至報警值，觸發液位控制系統響應，液位控制系統對泄漏速率的影響大致可分為3個階段：

① 泄漏速率Q下降，泄漏速率變化速度v上升且為負數；

② 泄漏速率Q上升，泄漏速率變化速度v先上升后下降，先為正數后為負數。

③ 泄漏速率Q基本穩定，泄漏速率變化速度v=0，達到穩態泄漏。

對比可發現：由于液位控制系統對泄漏速率影響很大，原經典泄漏模型無法準確描述液位控制系統干預下的泄漏情況。改進模型可計算得到液位控制理論值，如圖3～圖7所示，液位控制實驗值與改進模型理論值擬合較好，最大誤差不超過 5%。因此，改進的液位控制系統干預下的儲罐小孔泄漏速率模型更符合實際過程，有效提高儲罐泄漏速率計算準確性。

2.4.2 泄漏系數修正 不同初始壓力液位控制理論值與實驗值之間的誤差見表 2。誤差隨著壓力下降而逐漸減小，由正偏差變成負偏差，分析認為造成這一現象的原因與泄漏系數取值有關。如表2所示，當初始壓力為0.63、0.40、0.23 MPa時，泄漏系數取值0.65比較合適，而較高壓力下，泄漏系數取值0.65的相對誤差就比較大。

表2 不同初始壓力平均誤差Table 2 Average error of different initial pressure

泄漏系數主要反映泄漏孔處摩擦損失影響，在泄漏孔其他條件不變情況下，泄漏速度越快，與泄漏孔摩擦損失也就越大。壓力及液位高度直接影響泄漏速度。本實驗儲罐高度較小，當壓力較大時，液位對泄漏速率影響可以忽略，可認為壓力直接影響泄漏系數的取值。

因此，研究提出一種5 mm圓孔高壓泄漏系數修正方法，利用不同壓力下無控制儲罐泄漏速率實驗值，結合實時壓力、實時液位數據，得到壓力與泄漏系數的變化關系如圖8所示，擬合得到泄漏系數隨壓力動態變化公式

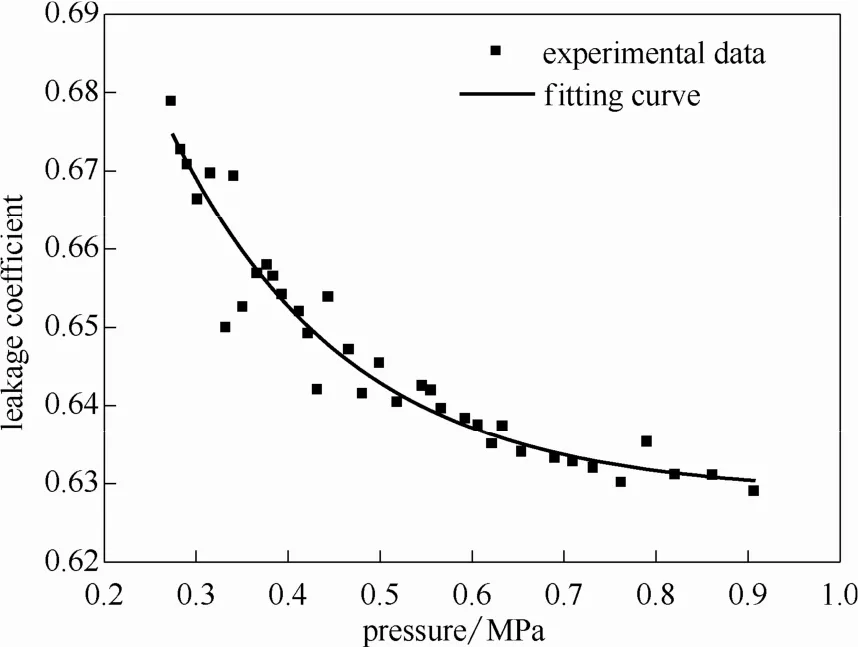
圖8 泄漏系數與壓力關系曲線Fig.8 Relationship curve of pressure and leakage coefficient

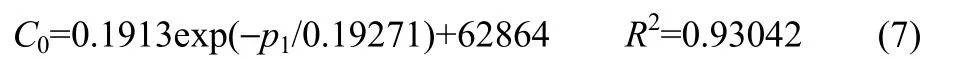
2.4.3 液位控制系統干預下儲罐小孔泄漏模型修正依據泄漏系數公式對液位控制系統干預下的小孔泄漏模型進行修正。將式(4)代入式(7)中得

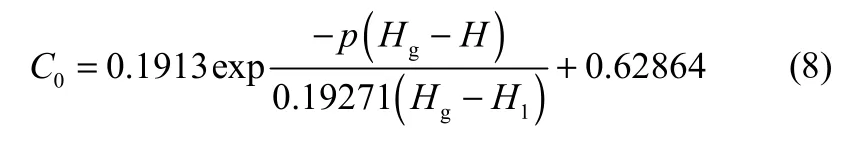
將式(8)代入式(5)得到液位控制系統動作前和調節過程中公式為

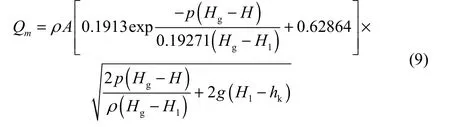
將式(8)代入式(6)得到液位控制系統動作后穩態泄漏公式為

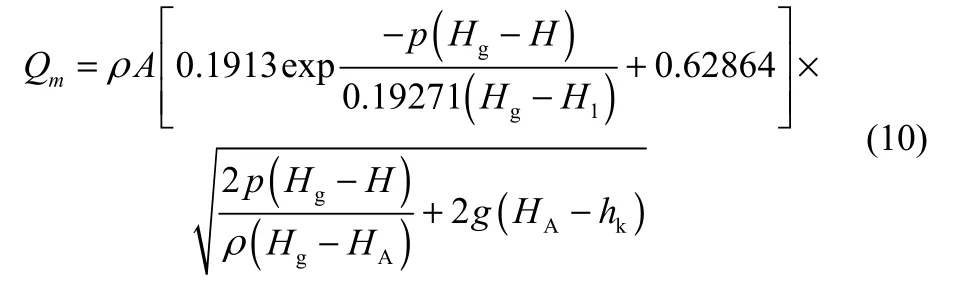
式(9)和式(10)為修正后的液位控制干預下的高壓小孔泄漏模型，利用修正后模型計算初始壓力為1.00、0.83 MPa時液位控制系統干預下的泄漏速率，并與未修正的理論值進行對比，如圖9、圖10所示。

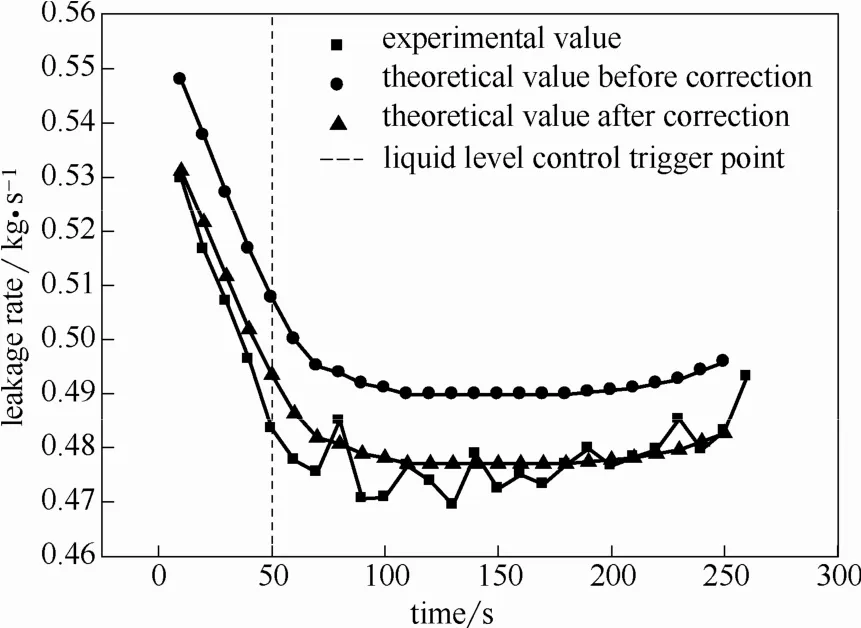
圖9 1.00 MPa修正后泄漏速率曲線Fig.9 Revised leakage rate curve of 1.00 MPa

對比修正前后理論值可發現，修正后的理論值擬合更好，相對誤差更小。初始壓力1.00 MPa修正后平均誤差為+0.1%，初始壓力0.83修正后平均誤差為?1.0%，修正后理論值更符合實際情況。

2.4.4 液位控制系統干預下的儲罐小孔泄漏模型實際運用方法 液位控制系統干預下的儲罐小孔泄漏模型相比較其他儲罐泄漏模型更符合工藝實際，只需已知實時液位變化情況就可快速計算出液位控制系統干預下的泄漏速率，可操作性更強。對于設有液位控制的儲罐泄漏事故，可運用該模型來計算泄漏速率，從而估算泄漏總量，更精確地對泄漏事故后果進行評估。

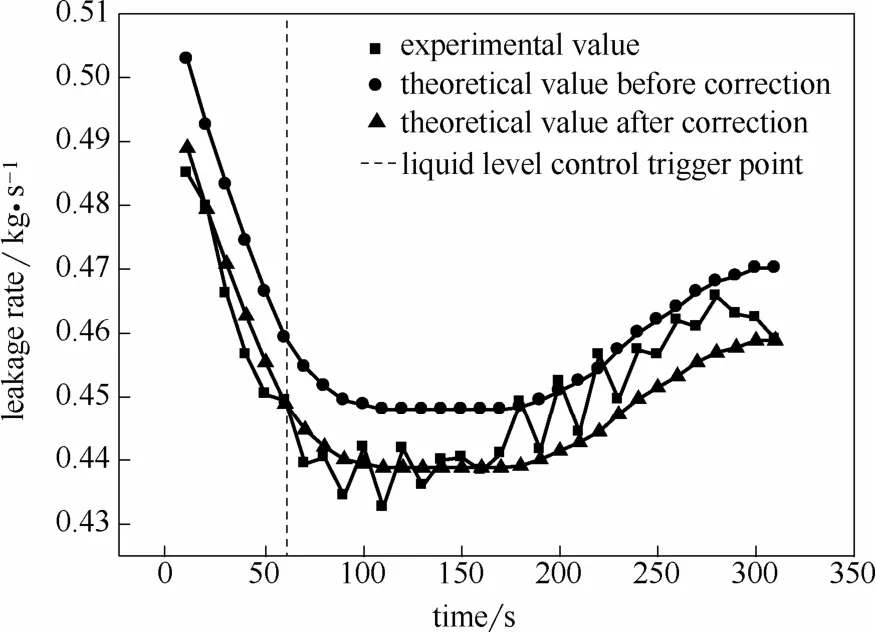
圖10 0.83 MPa修正后泄漏速率曲線Fig.10 Revised leakage rate curve of 0.83 MPa

泄漏事故發生后，在泄漏事故發生時間段內調取出泄漏事故過程中儲罐液位變化參數，運用方法如下。

（1）液位控制系統動作前，依據儲罐正常運行時罐內壓力（初始壓力）和液位（初始液位）參數，代入各時間點處的實時液位參數，計算出液位控制系統動作前泄漏速率，隨時間呈線性變化關系。

（2）液位控制系統動作后，波動階段，依據儲罐正常運行時罐內壓力（初始壓力）和液位（初始液位）參數，代入各時間點處的實時液位參數，計算出液位控制系統動作后，波動階段泄漏速率隨時間的變化關系。

（3）液位控制系統動作后，穩態泄漏階段，依據儲罐正常運行時罐內壓力（初始壓力）和液位（初始液位）參數，此階段儲罐內液位保持穩定，代入該定值計算出穩態泄漏過程中的泄漏速率。

（4）依據泄漏速率及泄漏時間計算泄漏總量。

3 結 論

（1）液位控制系統無法對泄漏事故起到保護作用，反而會增大泄漏速率，造成更加嚴重的事故后果，過程工藝中儲罐泄漏，進出流量對于泄漏速率的影響幾乎可以忽略，儲罐經典泄漏公式適用于連接在工藝系統中的儲罐泄漏。

（2）提出液位控制系統干預下的儲罐小孔泄漏速率模型，通過實驗驗證，該模型適用于設有液位控制系統的儲罐小孔泄漏情形，更符合工藝實際，且可操作性更強。

（3）以5 mm圓孔為例，提出高壓泄漏系數修正方法及修正后液位控制系統干預下的小孔泄漏模型，提出液位控制系統干預下的儲罐小孔泄漏模型實際運用方法。

[1]基于風險檢驗的基礎方法: SY/T 6714—2008 [S]. 國家發展和改革委員會, 2008. Risk-based inspection base resource document: SY/T 6714—2008 [S]. National Development and Reform Commission, 2008.

[2]WOODWARD J L, MUDAN K S. Liquid and gas discharge rates through holes in process vessels [J]. Journal of Loss Prevention in the Process Industries, 1991, 4(3): 161-165.

[3]CROWL D A. Liquid discharge from process and storage vessels [J]. Journal of Loss Prevention in the Process Industries, 1992, 5(2): 73-80.

[4]KORDESTANI S S, KUBIE J. Outflow of liquids from single-outlet vessels [J]. International Journal of Multiphase Flow, 1996, 22(5): 1023-1029.

[5]HART P W, SOMMERFELD J T. Fluid discharge resulting from puncture of spherical process vessels [J]. Journal of Hazardous Materials, 1993, 33(2): 295-305.

[6]LEE K S, SOMMERFELD J T. Maximum leakage times through puncture holes for process vessels of various shapes [J]. Journal of Hazardous Materials, 1994, 38(1): 27-40.

[7]FTHENAKIS V M, ROHATGI U S. A simple model for predicting the release of a liquid-vapor mixture from a large break in a pressurized container [J]. Journal of Loss Prevention in the Process Industries, 2003, 16: 61-72.

[8]BECK S B M, BAGSHAW N M, YATES J R. Explicit equations for leak rates through narrow cracks [J]. International Journal of Pressure Vessels and Piping, 2005, 82(7): 565-570.

[9]CASSA A M, VANZYL J E, LAUBSCHER R F. A numerical investigation into the effect of pressure on holes and cracks in water supply pipes [J]. Urban Water Journal, 2010, 7(2): 109-120.

[10]XIE L. The effect of characteristic crack sizes on the leak-before-break case of pressure vessels and piping with multiple cracks [J]. International Journal of Pressure Vessels and Piping, 1999, 76(7): 435-439.

[11]YANG Z D, BIN Q C, ZHU C, et al. Leak rates of high pressure steam-water across simulation crack [J]. Experimental Thermal and Fluid Science, 2014, 59: 118-126.

[12]WOODWARD J L. Validation of two models for discharge rate [J]. Journal of Hazardous Materials, 2009, 170: 219-229.

[13]LUO J H, ZHENG M, ZHAO X W, et al. Simplified expression for estimating release rate of hazardous gas from a hole on high-pressure pipelines [J]. Journal of Loss Prevention in the Process Industries, 2006, 19(4): 362-366.

[14]CHANG Y S, JEONG J U, KIM Y J, et al. Enhancement of leak rate estimation model for corroded cracked thin tube [J]. Pressure Vessels and Piping, 2010, 87: 52-58.

[15]LU J S, YANG Z B, WU H X. Model experiment on the dynamic process of oil leakage from the double hull tanker [J]. Journal of LossPrevention in the Process Industries, 2016, 43: 174-180.

[16]潘旭海, 蔣軍成. 事故泄漏源模型研究與分析[J]. 南京工業大學學報(自然科學版), 2002, 24(1): 108-113. PAN X H, JIANG J C. Progress of accident release source and mechanism models [J]. Journal of Nanjing University of Technology, 2002, 24(1): 108-113.

[17]王大慶, 魏海燕. 壓力容器泄漏源模型的分析研究[J]. 石油工程建設, 2010, 36(5): 17-18. WANG D Q, WEI H Y. Analytical research on leakage source model of pressure vessel [J]. Petroleum Engineering Construction, 2010, 36(5): 17-18.

[18]沈遠勝, 劉宗明, 趙蔚琳, 等. 壓力容器泄漏孔大小的壓力變化率預估方法[J]. 熱能動力工程, 2010, 25(6): 653-656. SHEN Y S, LIU Z M, ZHAO W L, et al. A method for pre-estimating the size of leakage holes of a pressure vessel based on its pressure variation rate [J]. Journal of Engineering for Thermal Energy and Power, 2010, 25(6): 653-656.

[19]周超, 王志榮. 立式儲罐液體泄漏過程的模擬實驗[J]. 油氣儲運, 2011, 30(4): 310-313. ZHOU C, WANG Z R. Leakage process simulation of vertical tank [J]. Oil and Gas Storage and Transportation, 2011, 30(4): 310-313.

[20]任榮亭, 韓兵奇, 韓正偉, 等. 壓力容器液相流體泄漏實驗研究[J].液壓氣動與密封, 2013, (7): 12-14. REN R T, HAN B Q, HAN Z W, et al. Experimental study about the liquid leakage of pressure vessels [J]. Hydraulics Pneumatics and Steals, 2013, (7): 12-14.

[21]李金光, 鄭建華, 高賢. 全容式 LNG儲罐內罐泄漏源模型[J]. 油氣儲運, 2012, 31(10): 777-779. LI J G, ZHENG J H, GAO X. Leakage source model of internal tank of full capacity LNG storage tank [J]. Oil and Gas Storage and Transportation, 2012, 31(10): 777-779.

[22]丹尼爾 A. 克勞爾, 約瑟夫 F. 盧瓦爾. 化工過程安全理論及應用[M]. 蔣軍成, 潘旭海, 譯. 北京: 化學工業出版社, 2006: 71-72. CROWL D A, LOUVAR J F. Chemical Process Safety Fundamentals with Applications [M]. JIANG J C, PAN X H, trans. Beijing: Chemical Industry Press, 2006: 71-72.

[23]蔣軍成. 事故調查與分析技術[M]. 北京: 化學工業出版社, 2009: 216. JIANG J C. Accident Investigation and Analysis Technology [M]. Beijing: Chemical Industry Press, 2009: 216.

[24]化工企業定量風險評價導則: AQ/T 3046—2013 [S]. 北京: 煤炭工業出版社, 2013. Guidelines for quantitative risk assessment of chemical enterprises: AQ/T 3046—2013 [S]. Beijing: China Coal Industry Publishing House, 2013.

Hole-leakage rate model of whole process based on intervention of liquid level control system

FU Jianmin1, ZHANG Bolun1,2, CHEN Guoming1, ZHENG Xiaoyun1, YE Chuang1, GUO Chao1, ZHU Yuan1
(1Centre for Offshore Engineering and Safety Technology, China University of Petroleum, Qingdao 266580, Shandong, China;2Dalian Port (PDA) Company Limited, Dalian 116600, Liaoning, China)

Leakage rate is the premise and basis of leakage mass calculation, leakage duration determination and leak risk assessment. Through building a tank experiment system of liquid hole-leakage for different leak scenes and contrasting the variation of the leakage rate under the interventions of the liquid level control system, an analysis is carried out combined with the calculation of leakage rate model. The result shows that after the response of liquid level control system, the leakage rate reduces slowly and gradually increases as time goes on. Finally, the leakage rate stays in a stable leakage state. The influence of the flow rate on the hole-leakage rate of the tank can be neglected. Hole-leakage rate model of tank based on the actual liquid level control system is built through improving classic formula of tank leakage. The calculation method and the model of high pressure hole-leakage correction coefficient are proposed. By verification, the model can efficiently improve the calculation accuracy under the interventions of the liquid level control system.

liquid level control; leakage rate; model; experimental validation; safety

FU Jianmin, fujianmin@126.com

X 937

：A

：0438—1157（2017）01—0473—08

10.11949/j.issn.0438-1157.20160506

2016-04-19收到初稿，2016-09-28收到修改稿。

聯系人及第一作者：付建民（1977—），男，博士，副教授。

青島市民生科技計劃重點支持項目（14-2-3-64-nsh）；中央高校基本科研業務費專項資金項目（1515CX05018A）。

Received date: 2016-04-19.

Foundation item: supported by the Qingdao Minsheng Science and Technology Key Support Project (14-2-3-64-nsh) and the Central Universities Fundamental Research Funds Project (1515CX05018A).