立足“基本” 輕松迎考

王立

方程與不等式是初中代數的主干知識，是后續學習的重要基礎.不等式與方程、函數的綜合應用充分體現了相等與不等的對立與統一的辯證關系.此類中考試題都是緊扣新課程標準，重基礎，重考查最基本的數學能力.希望同學們能夠立足“基本”，輕松迎考.

一、從“直觀出發”，發現自然解法

例1 （2016·山東東營）如圖，直線y=x+b與直線y=kx+6交于點P（3，5），則關于x的不等式x+b>kx+6的解集是 .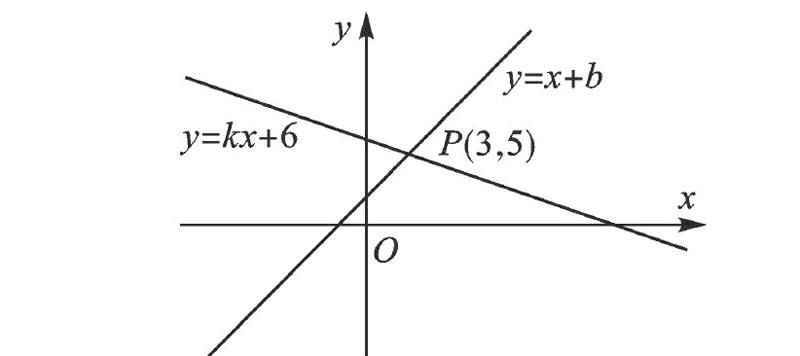

【解析】本題考查了一次函數與一元一次不等式的關系.從函數的角度看，就是尋求使一次函數y=x+b的值大于y=kx+6的自變量x的取值范圍；從函數圖像的角度看，就是確定直線y=x+b在直線y=kx+6的上方的部分所有的點的橫坐標所構成的集合.

解：由圖像得到直線y=x+b與直線y=kx+6的交點P（3，5），在點P（3，5）的右側，直線y=x+b落在直線y=kx+6的上方，該部分對應的x的取值范圍為x>3，即不等式x+b>kx+6的解集是x>3.

【小試身手】1.將函數y=2x+b（b為常數）的圖像位于x軸下方的部分沿x軸翻折至其上方后，所得的折線是函數y=[2x+b]（b為常數）的圖像.若該圖像在直線y=2下方的點的橫坐標x滿足0

二、從“基本經驗”出發，尋找突破口

例2 （2016·浙江寧波）某商場銷售A，B兩種品牌的教學設備，這兩種教學設備的進價和售價如表所示.

該商場計劃購進兩種教學設備若干套，共需66萬元，全部銷售后可獲毛利潤9萬元.

（1）該商場計劃購進A，B兩種品牌的教學設備各多少套？

（2）通過市場調研，該商場決定在原計劃的基礎上，減少A種設備的購進數量，增加B種設備的購進數量，已知B種設備增加的數量是A種設備減少的數量的1.5倍.若用于購進這兩種教學設備的總資金不超過69萬元，問A種設備購進數量至多減少多少套？

【解析】此題考查了一元一次不等式與二元一次方程組的應用.注意根據題意找到等量關系是關鍵.

（1）設該商場計劃購進A，B兩種品牌的教學設備分別為x套，y套，根據題意可列方程組，解此方程組即可；

（2）設A種設備購進數量減少a套，則B種設備購進數量增加1.5a套，根據題意可列不等式，解不等式即可求得答案.

解：（1）設該商場計劃購進A，B兩種品牌的教學設備分別為x套，y套，

[1.5x+1.2y=66，0.15x+0.2y=9，]解得：[x=20，y=30.]

答：該商場計劃購進A，B兩種品牌的教學設備分別為20套，30套.

（2）設A種設備購進數量減少a套，則B種設備購進數量增加1.5a套，

1.5（20-a）+1.2（30+1.5a）≤69，

解得：a≤10.

答：A種設備購進數量至多減少10套.

【小試身手】2.大學生小劉回鄉創辦小微企業，初期購得原材料若干噸，每天生產相同件數的某種產品，單件產品所耗費的原材料相同.當生產6天后剩余原材料36噸，當生產10天后剩余原材料30噸.若剩余原材料數量小于或等于3噸，則需補充原材料以保證正常生產.

（1）求初期購得的原材料噸數與每天所耗費的原材料噸數；

（2）若生產16天后，根據市場需求每天產量提高20%，則最多再生產多少天后必須補充原材料？

3.（2015·四川樂山）“六一”期間，小張購進100只兩種型號的文具進行銷售，其進價和售價之間的關系如下表：

（1）小張如何進貨，使進貨款恰好為1300元？

（2）要使銷售文具所獲利潤最大，且所獲利潤不超過進貨價格的40%，請你幫小張設計一個進貨方案，并求出其所獲利潤的最大值.

三、從“基本思想”出發，實施轉化

例3 （2015·廣東廣州）已知A=[x2+2x+1x2-1]

-[xx-1].

（1）化簡A；

（2）當x滿足不等式組[x-1≥0，x-3<0]且x為整數時，求A的值.

【解析】此題主要考查分式的化簡求值，注意化簡時不能跨度太大而缺少必要的步驟，會失得分點.此題還考查了求一元一次不等式組的整數解問題，要熟練掌握，解決此類問題的關鍵在于正確求出不等式的解集，然后再根據題目中對于解集的限制得到下一步所需要的條件，最后求得不等式組的整數解即可.

解：（1）A=[x2+2x+1x2-1]-[xx-1]

=[x+12x+1x-1]-[xx-1]

=[x+1x-1]-[xx-1]

=[1x-1].

（2）∵[x-1≥0，x-3<0，]∴[x≥1，x<3，]

∴1≤x<3，

∵x為整數，

∴x=1或x=2.

①當x=1時，

∵x-1≠0，

∴A=[1x-1]中x≠1，

∴當x=1時，A=[1x-1]無意義.

②當x=2時，

A=[1x-1]=[12-1]=1.

【小試身手】4.早晨，小明步行到離家900米的學校去上學，到學校時發現眼鏡忘在家中，于是他立即按原路步行回家，拿到眼鏡后立即按原路騎自行車返回學校.已知小明步行從學校到家所用的時間比他騎自行車從家到學校所用的時間多10分鐘，小明騎自行車速度是步行速度的3倍.

（1）求小明步行速度（單位：米/分）是多少；

（2）下午放學后，小明騎自行車回到家，然后步行去圖書館，如果小明騎自行車和步行的速度不變，小明步行從家到圖書館的時間不超過騎自行車從學校到家時間的2倍，那么小明家與圖書館之間的路程最多是多少米？

5.某地2014年為做好“精準扶貧”，投入資金1280萬元用于異地安置，并規劃投入資金逐年增加，2016年在2014年的基礎上增加投入資金1600萬元.

（1）從2014年到2016年，該地投入異地安置資金的年平均增長率為多少？

（2）在2016年異地安置的具體實施中，該地計劃投入資金不低于500萬元用于優先搬遷租房獎勵，規定前1000戶（含第1000戶）每戶每天獎勵8元，1000戶以后每戶每天補助5元，按租房400天計算，試求今年該地至少有多少戶享受到優先搬遷租房獎勵？

6.某商家預測一種應季襯衫能暢銷市場，就用13200元購進了一批這種襯衫，面市后果然供不應求，商家又用28800元購進了第二批這種襯衫，所購數量是第一批購進量的2倍，但單價貴了10元.

（1）該商家購進的第一批襯衫是多少件？

（2）若兩批襯衫按相同的標價銷售，最后剩下50件按八折優惠賣出，如果兩批襯衫全部售完利潤率不低于25%（不考慮其他因素），那么每件襯衫的標價至少是多少元？

（作者單位：江蘇省連云港市海州實驗中學）