NEW LOWER BOUNDS FOR LEE DISCREPANCY ON TWO AND THREE MIXED LEVELS FACTORIALS?

Shuo SONG(宋碩)

College of Science,Wuhan University of Science and Technology,Wuhan 430065,China

Qionghui ZHANG(張瓊慧)

Faculty of Mathematics and Statistics,Central China Normal University,Wuhan 430079,China

Na ZOU(鄒娜)

School of Statistics and Mathematics,Zhongnan University of Economics and Law, Wuhan 430073,China

Hong QIN(覃紅)?

Faculty of Mathematics and Statistics,Central China Normal University,Wuhan 430079,China

NEW LOWER BOUNDS FOR LEE DISCREPANCY ON TWO AND THREE MIXED LEVELS FACTORIALS?

Shuo SONG(宋碩)

College of Science,Wuhan University of Science and Technology,Wuhan 430065,China

E-mail:songshuo@wust.edu.cn

Qionghui ZHANG(張瓊慧)

Faculty of Mathematics and Statistics,Central China Normal University,Wuhan 430079,China

E-mail:zhangqionghui865@163.com

Na ZOU(鄒娜)

School of Statistics and Mathematics,Zhongnan University of Economics and Law, Wuhan 430073,China

E-mail:zounamail@126.com

Hong QIN(覃紅)?

Faculty of Mathematics and Statistics,Central China Normal University,Wuhan 430079,China

E-mail:qinhong@mail.ccnu.edu.cn

The objective of this paper is to study the issue of uniformity on asymmetrical designs with two and three mixed levels in terms of Lee discrepancy.Based on the known formulation,we present a new lower bound of Lee discrepancy of fractional factorial designs with two and three mixed levels.Our new lower bound is sharper and more valid than other existing lower bounds in literature,which is a useful complement to the lower bound theory of discrepancies.

U-type design;Lee discrepancy;uniform design;lower bound

2010 MR Subject Classifcation 62K15;62K05

1 Introduction

Uniform designs are important methods of computer experiments and robust experimental designs,which spread experimental points uniformly on the experimental domain.The measure of uniformity plays a key role in the construction of uniform designs.Many discrepancies in quasi-Monte Carlo methods were employed to measure the uniformity of designs.For details, we can refer to[4].A design with the smallest discrepancy value is called a uniform design.Among these discrepancies,the Lee discrepancy proposed by[5]was regarded more reasonable and practicable.In this paper,we use Lee discrepancy as the uniformity measure.

Recently,there was considerable interest in exploring the issue of lower bounds for Lee discrepancy,because lower bounds of Lee discrepancy can be used as a benchmark not only in searching for uniform designs but also in helping to validate that some good designs are in fact uniform or not.Many authors tried to fnd lower bounds to Lee discrepancy so as to obtain most efcient designs.Obviously,a design whose Lee discrepancy value achieves a strict lower bound is a uniform design with respect to this discrepancy.[5]gave some lower bounds for both symmetric and asymmetric U-type designs.[6]provided two improved lower bounds of Lee discrepancy of fractional factorials with two or three levels.[2]obtained a lower bound of Lee discrepancy of asymmetrical factorials with two-and three-levels.[7]studied the uniformity in terms of Lee discrepancy of double designs.Note that two and three mixed levels factorials are most popular among mixed factorials.The present paper aims at obtaining some improved lower bounds for the Lee discrepancy on factorials with two and three mixed levels.

The remainder of this paper is organized as follows:Section 2 provides the notations and preliminaries.In Section 3,lower bounds for Lee discrepancy are provided.Some illustrative examples are provided in Section 4.

2 Notations and Preliminaries

An m-level U-type design belonging to a class U(n;ms)of designs is an n×s array with entries from the set{0,1,···,m?1}such that in each column each of entries of the set {0,1,···,m?1}appears equally often.A U-type design with s1two-level factors and s2threelevel factors belonging to a class U(n;2s13s2)of designs corresponds to an n×s(s=s1+s2) array X=(x1,···,xs)such that each of entries in each column xi(1≤i≤s1)takes values from a set of{0,1}equally often,and each of entries in xi(s1+1≤i≤s)takes values from a set of{0,1,2}equally often.

For any design d∈U(n;2s13s2),according to[5],Lee-discrepancy value of d,denoted by LD(d),can be calculated by the following formula

where for i,j=1,···,n,

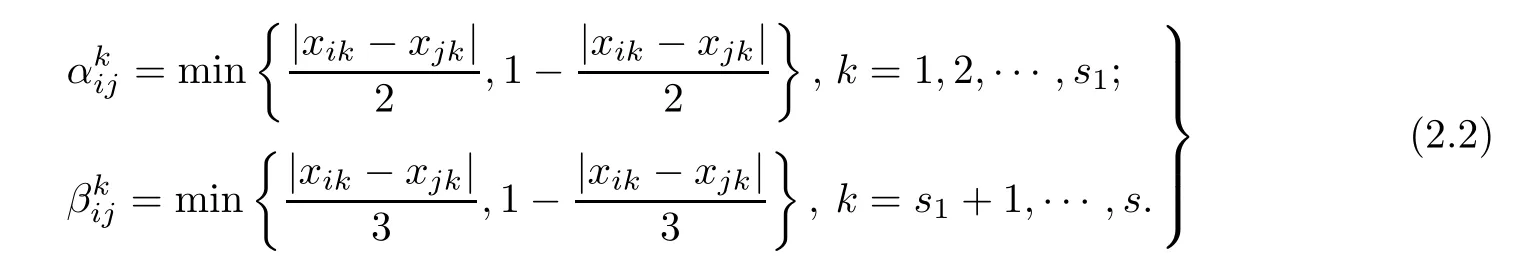
For any design d∈U(n;ms)and its corresponding n×s matrix(x1,x2,···,xs),where xj=(x1j,x2j,···,xnj)T,we defne

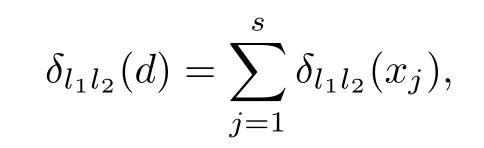
where δl1l2(xj)is the Kronecker delta function,equal to 1 if xl1j=xl2jand 0 otherwise.Then we call δl1l2(d)as the coincidence number of the l1th and l2th rows for d.

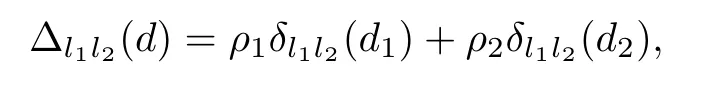
where ρ1>0 and ρ2>0 are weights.We call?l1l2(d)the weighted coincidence number of the l1th and l2th rows for d.

3 Main Results

In this section,we discuss lower bounds of Lee discrepancy for asymmetrical factorials of two and three levels.The lower bound obtained by[2]is the frst attempt on mixed-level factorials.We state their result as follows.

Theorem 3.1(see[2]) For any design d∈U(n;2s13s2),we have

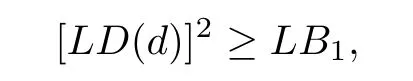
where

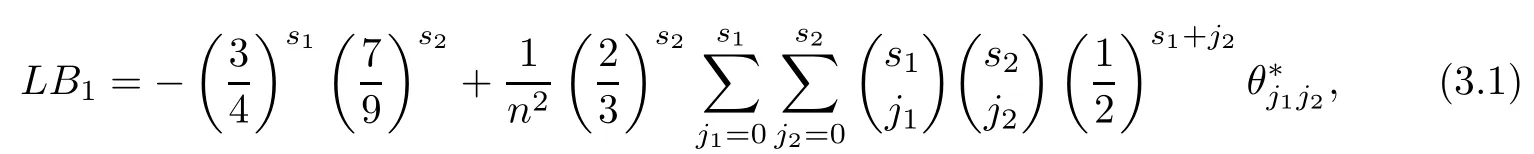
In order to give another lower bound of Lee discrepancy for mixed-level designs,we need the following two important lemmas.

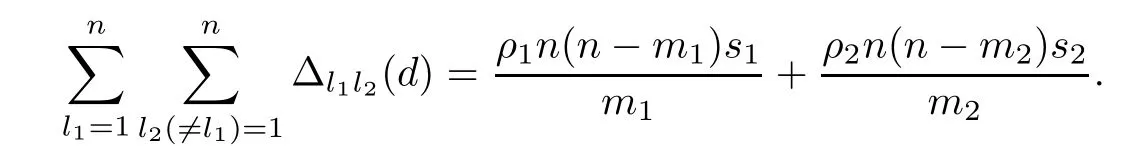
Lemma 3.3 For any design d∈U(n;2s13s2),and any positive integer t,we have

By Lemma 3.3,we can deduce a new lower bound of Lee discrepancy for asymmetrical factorials of two and three levels.

Theorem 3.4 For any design d∈U(n;2s13s2),we have

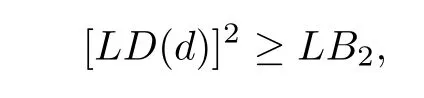
where

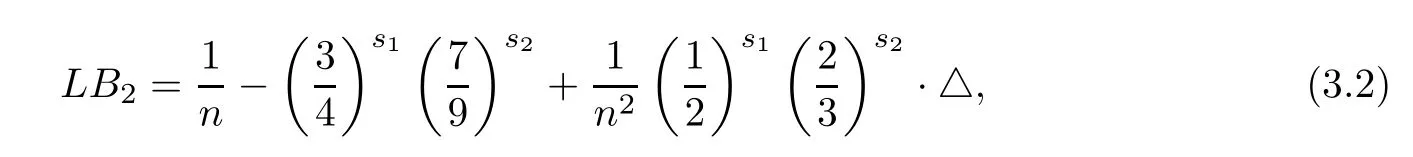
and

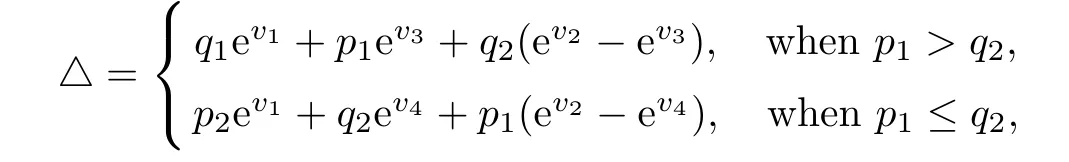
Proof By(2.2)we know that,for 1≤ k≤s1,whenotherwiseFurthermore

For s1+1≤k≤s,whenhence

Then,(2.1)can be written as

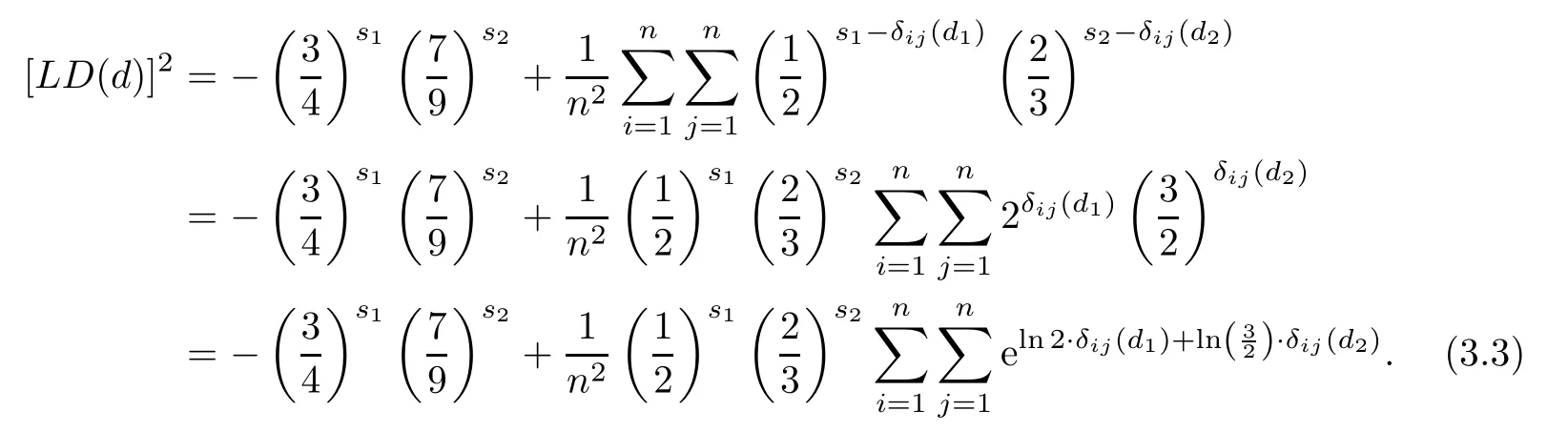
Let ρ1=ln2,ρ2=ln(3/2),then?ij(d)= ρ1δij(d1)+ρ2δij(d2)is a weighted coincidence number of the ith and jth row of d.Notice that?ii(d)=ρ1s1+ρ2s2,i=1,···,n.Following (3.3),we have

It is to be noted that

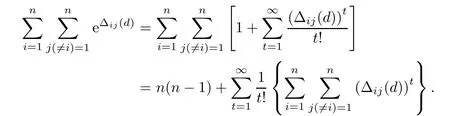
By use of Lemma 3.3 and some algebra calculus,we can get(3.2),which completes the proof. ?

In order to compare the diference between LB2and LB1,we give some fgures below and examples in the next section.Figures 1 and 2 show how the diference between LB2and LB1varies by n,s2(or n,s1)when s1(or s2)is fxed.From these fgures and examples in the next section,we could conclude empirically that LB2is larger than LB1in most cases,and when s1or s2gets bigger,the diference between LB2and LB1intends to get bigger.

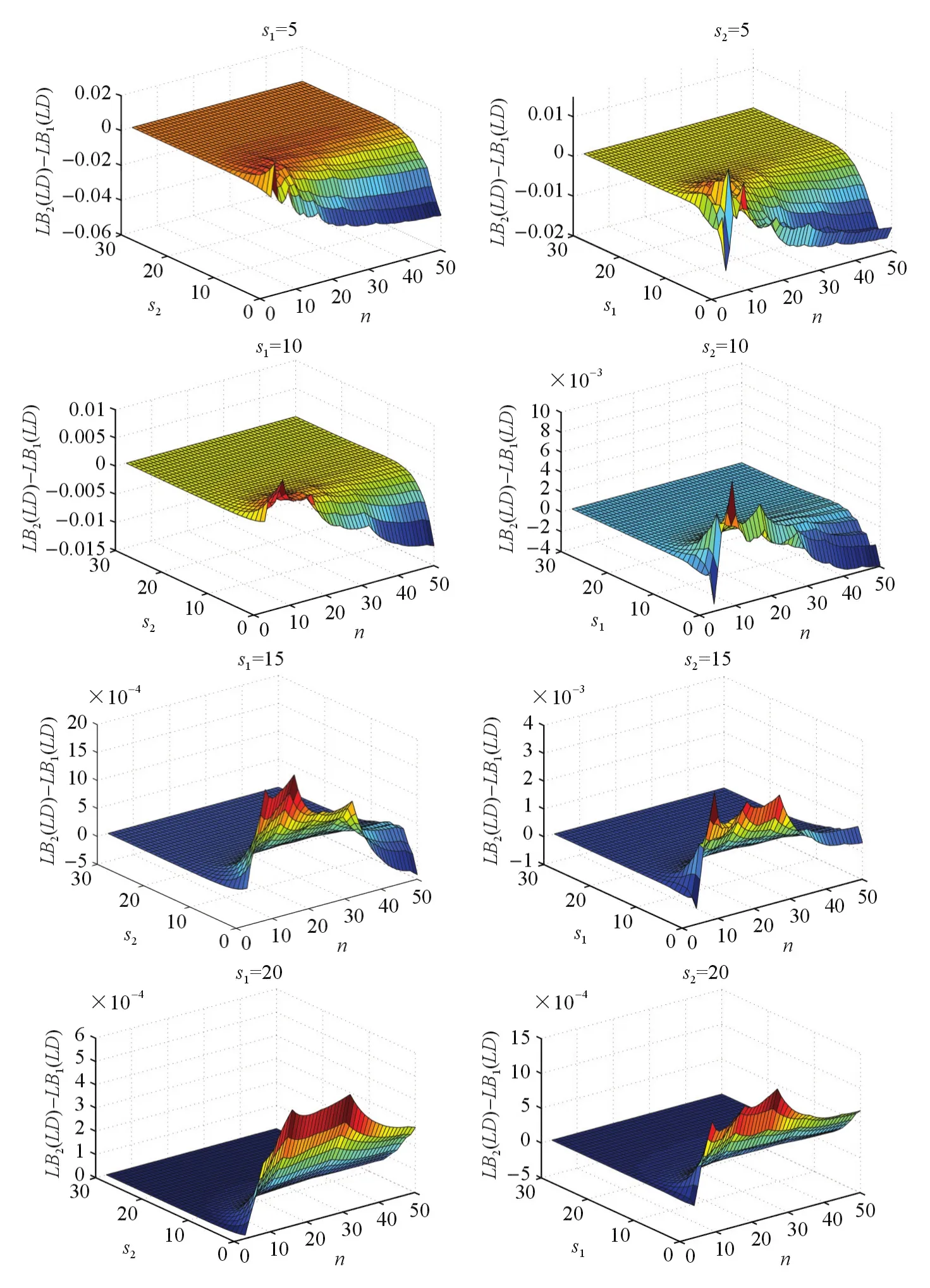
Figure 1 Diference between LB1and LB2

Figure 2 Diference between LB1and LB2continued

Combine Theorems 3.1 and 3.4,we can get an improved lower bound of Lee discrepancy for any design with two and three mixed levels.

Theorem 3.5Consider any design d∈U(n;2s13s2),then

where LB=max{LB1,LB2}.

Note that,if s1=0 or s2=0,Theorem 3.4 still holds.As a consequence,we can easily get the following corollary.

Corollary 3.6Consider any design d∈U(n;ms),

(1)when m=2,we have

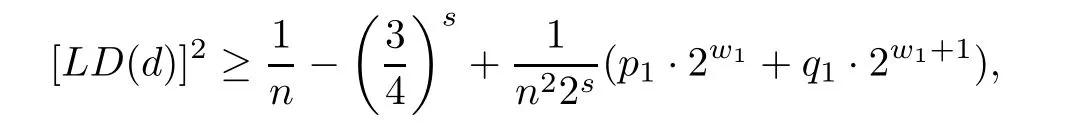
where

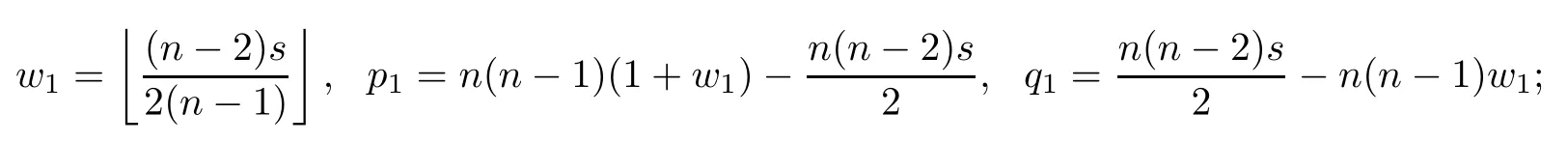
(2)when m=3,we have

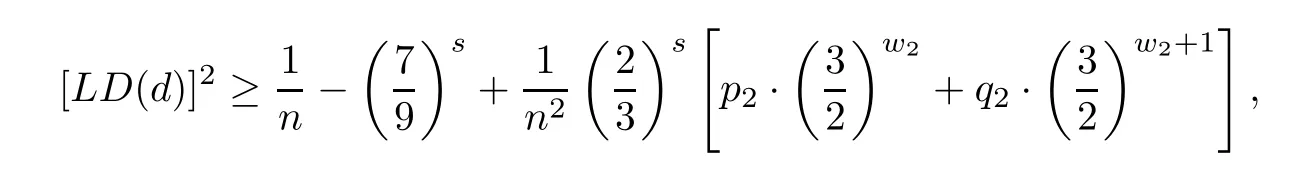
where

4 Numerical Studies

Example 4.1Take n=18,s1=1,s2=7,8,9.Table 1 shows three U-type designs denoted by d18,1,7,d18,1,8,d18,1,9respectively,the numerical results are also shown in Table 1. It is easily to see that the new lower bounds behave better than the old ones.

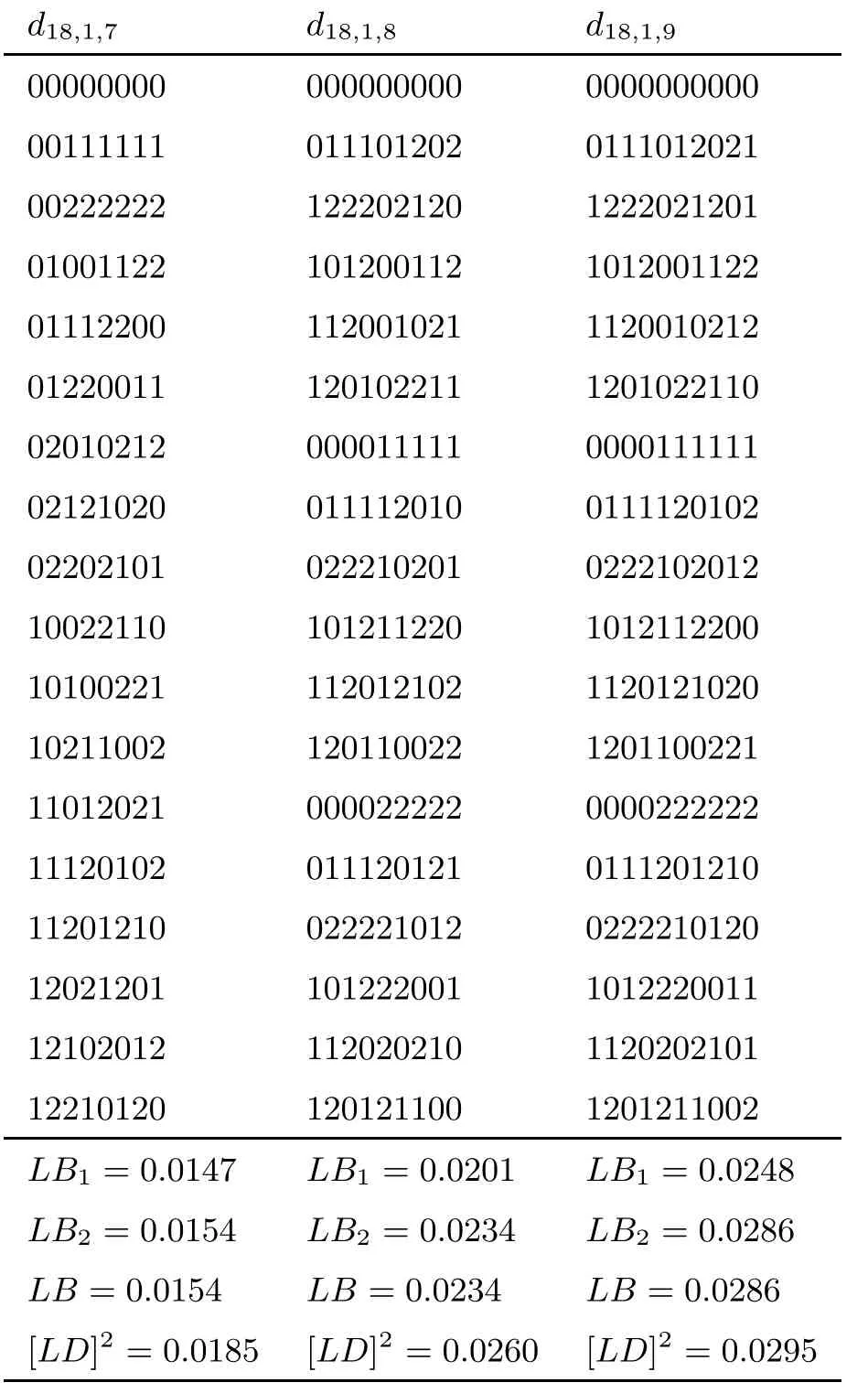
Table 1 18-run asymmetrical factorial of two and three level

Example 4.2Take n=12,s1=3,s2=4,5,6.Table 2 shows three U-type designs denoted by d12,3,4,d12,3,5,d12,3,6,respectively,the numerical results are also shown in Table 2. It is easily to see that LB2is bigger than LB1,the new lower bounds behave better than the old ones.

Example 4.3Take n=12,s2=5,s1=10,11,12.Table 3 shows three U-type designs denoted by d12,10,5,d12,11,5,d12,12,5respectively,the numerical results are also shown in Table 3.It is also easily to see that the new lower bounds behave better than the old ones.

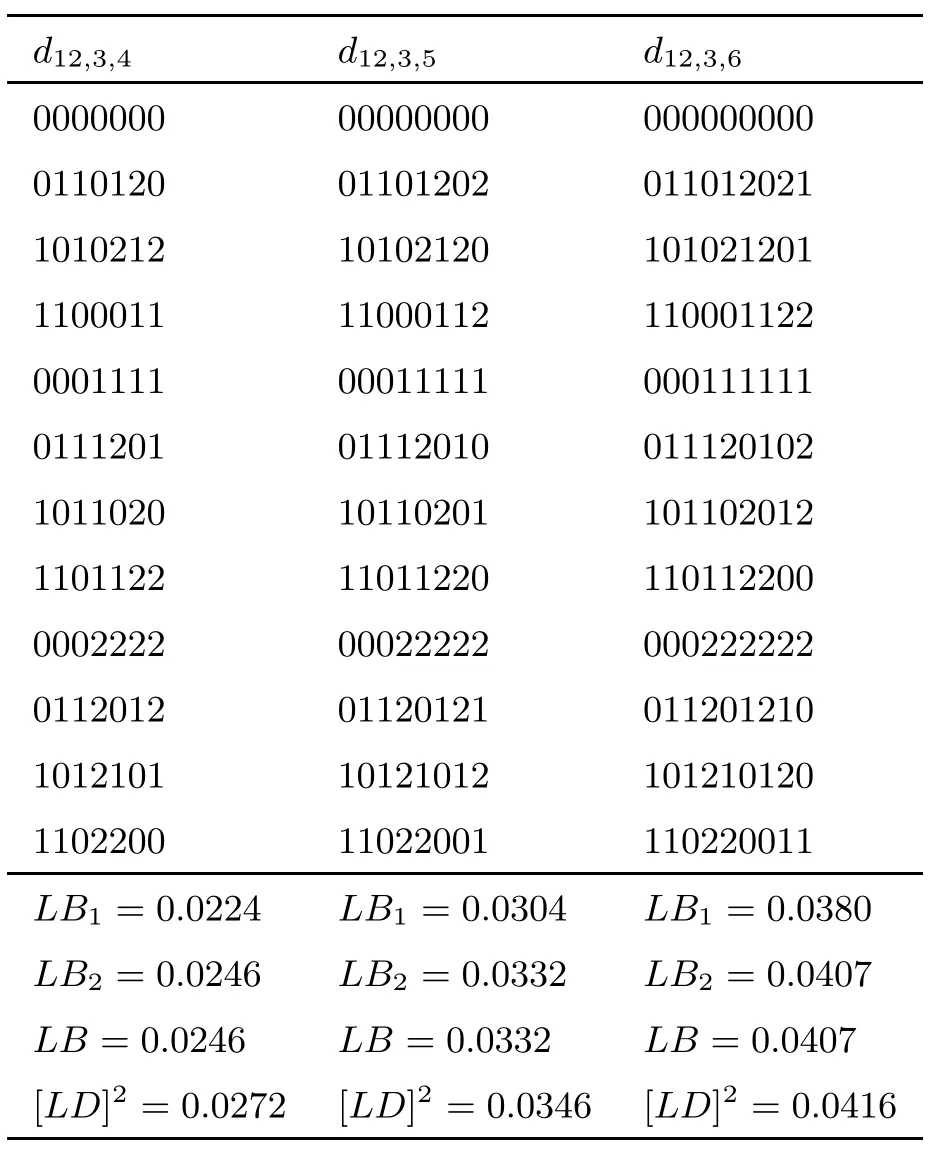
Table 2 12-run asymmetrical factorial of two and three level

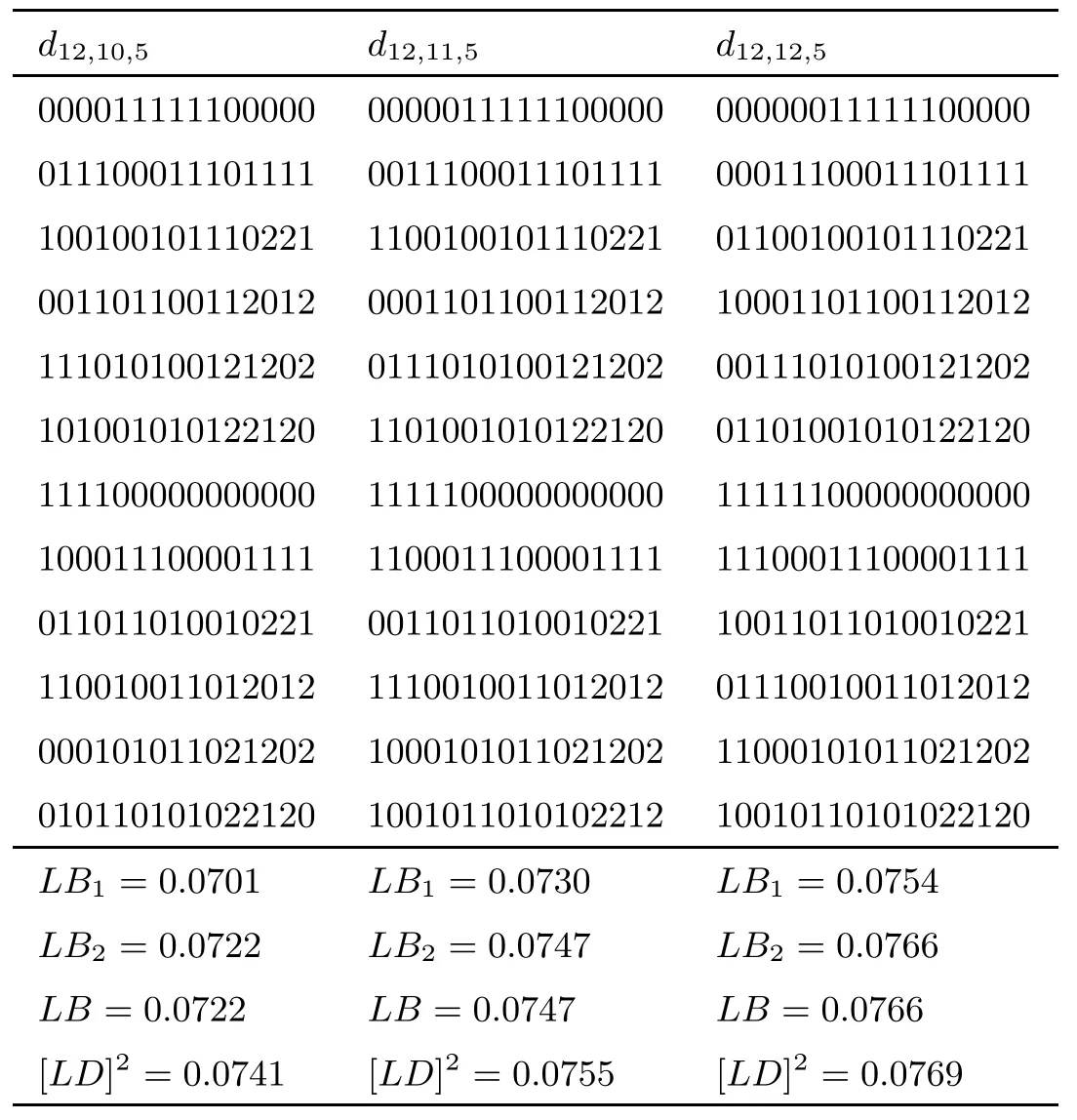
Table 3 12-run asymmetrical factorial of two and three level

[1]Chatterjee K,Li Z H,Qin H.Some new lower bounds to centered and wrap-around L2-discrepancies.Statist Probab Letters,2012,82:1367–1373

[2]Chatterjee K,Qin H,Zou N.Lee discrepancy on asymmetrical factorials with two-and three-levels.Science China Mathematics,2012,55:663–670

[3]Elsawah M A,Qin H.New lower bound for centered L2-discrepancy of four-level U-type designs.Statist Probab Letters,2014,93:65–71

[4]Fang K T,Li R,Sudjianto A.Design and Modelling for Computer Experiments.London:Chapman and Hall,2005

[5]Zhou Y D,Ning J H,Song X B.Lee discrepancy and its applications in experimental designs.Statist Probab Letters,2008,78:1933–1942

[6]Zou N,Ren P,Qin H.A note on Lee discrepancy.Statist Probab Letters,2009,79:496–500

[7]Zou N,Qin H.Some properties of double designs in terms of Lee discrepancy.Acta Matematica Scientia, accepted,2016

?Received January 24,2015;revised May 3,2016.The third author was supported by the National Natural Science Foundation of China(11301546).The fourth author is supported by the National Natural Science Foundation of China(11271147,11471136).

?Corresponding author:Hong QIN.