基于幾何代數的時空宗地meet計算研究

王巧燕，蔣曉敏，張 豐*，杜震洪，劉仁義

(1. 浙江大學 浙江省資源與環境信息系統重點實驗室， 浙江 杭州 310028；2. 浙江大學 地球科學學院， 浙江 杭州 310027)

基于幾何代數的時空宗地meet計算研究

王巧燕1,2，蔣曉敏1,2，張 豐1,2*，杜震洪1,2，劉仁義1,2

(1. 浙江大學 浙江省資源與環境信息系統重點實驗室， 浙江 杭州 310028；2. 浙江大學 地球科學學院， 浙江 杭州 310027)

根據幾何代數在地理空間對象建模和多維數據分析應用的特點，研究了共形幾何代數交/并(meet/join)算子的含義、構建和應用.利用幾何代數多維統一、高維計算適應的優勢，設計了基于幾何代數meet算子和有向半空間劃分理論的時空宗地meet算法.從三維地籍和時空數據建模出發，在共形幾何代數和時空代數范疇中，給出了三維、四維時空宗地的定義和表達.同時，以宗地數據的拓撲計算為例，將該算法運用于三維時空宗地拓撲計算場景——歷史回溯中，取得了良好的效果.該算法的理念同樣適用于四維時空宗地的歷史回溯meet求解.

幾何代數；時空拓撲關系計算；meet算子；時空宗地求交

A study on meet computation of spatio-temporal parcel based on conformal geometric algebra. Journal of Zhejiang University(Science Edition), 2017,44(1):076-082

幾何代數，是用代數的語言來描述和表達圖形的操作，通過引入Clifford積，實現幾何不變量和協變量的代數表示和計算[1].憑借共形幾何代數與坐標無關及多維統一的高效運算等特性，其被引入多維時空的統一表達與分析，并可進行不依賴于坐標的高維空間幾何計算[2].時空GIS建模和表達需要從時空觀和基礎數學理論進行革新.羅文等[3]在共形幾何代數框架中對地理空間的多維對象進行了建模，實現了三維場景的可視化和交互操作.宗真等[4]利用與Grassman分級結構一致的幾何代數外積表達，構建了三角網模型，同時研究了三角網meet求交算法，并將其應用于南極冰蓋消融平衡線的模擬計算.

本文從三維地籍和時空數據建模出發，分析現下地籍時空數據在建模和時空分析中的限制[5-8]，將幾何代數理論用于時空宗地的建模和表達中，同時設計相應的時空宗地meet算子，并將其應用于時空宗地的拓撲關系計算.最后，以建德市白沙村約20 a的時空宗地數據為例進行建模，實現宗地歷史回溯場景的求解.

1 時空宗地幾何代數表達和meet算子構建

1.1 時空宗地的幾何代數表達

“時空宗地”一詞最早由史云飛等[9]在進行四維地籍的研究時提出，時空宗地是由宗地權屬邊界(包括時間邊界和空間邊界)對四維時空或三維時空進行剖分而形成的時空單元.根據時空宗地空間邊界的不同形態，目前實際存在的時空宗地有三維和四維2種，三維時空宗地指地表宗地+時間維，其空間邊界為二維多邊形，幾何表現為以宗地空間邊界圍成的多邊形為底、以量化后的生存時間總長為棱的棱柱(見圖1)；四維時空宗地指地上或地下宗地+時間維，空間邊界為三維多面體，用來描述四維時空宗地幾何形狀的單位幾何體是超立方體，其時間t軸同時垂直于x、y、z軸，每個三維宗地實體的面是一個以生存時間總長為棱的棱柱的底面(見圖2).

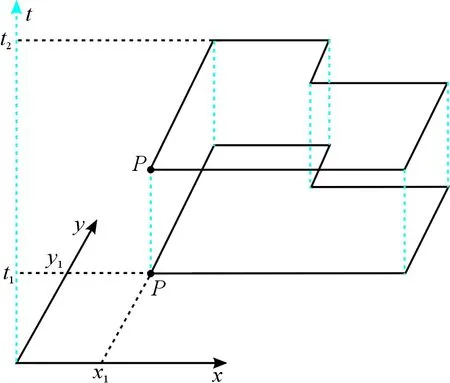
圖1 三維時空宗地幾何形態Fig.1 Three-dimensional geometry of spatio-temporal parcel

圖2 四維時空宗地幾何形態(投影后)Fig.2 Four-dimensional geometry ofspatio-temporal parcel

時空宗地的立方體模型與幾何代數的正交基組向量表示形式一致，幾何代數在三維時空中，使用3個正交基向量e1，e2，e3表達時空單點P：

P=x·e1+y·e2+ct·e3.

(1)

而共形幾何代數則是在此基礎上引入零點e0和無窮遠點e∞，構建共形空間C3，提高子空間的表達能力，實現點、直線、平面、圓、球等對象的基本表達.同理，幾何代數往四維時空擴展，被稱為時空代數，時空代數中使用4個正交基向量：e1，e2，e3，e4對時空單點進行表達[10-13]:

P=x·e1+y·e2+z·e3+ct·e4.

(2)

1.2 時空宗地meet算子構建

Meet關系在時空拓撲中意指相接關系，由于時空宗地是對四維時空的連續覆蓋[14]，meet關系是時空宗地重要的時空拓撲關系，不僅可以用來研究2個時空宗地間的時空關系，還可以用來研究時空宗地的自身演化過程，甚至，考慮到時空宗地的特殊性，meet計算能夠在特定視角實現對時空宗地的剖分和觀察.故而，本文所定義的meet算子不僅可用于時空相接關系的計算，還可用于時空元素，例如時空切面、時空切體與時空宗地的時空相交關系計算，是適應多維和高維共形幾何代數的meet算子，在地理時空分析領域可具體實現和擴展.

1.2.1 幾何代數meet算子和half-space理論

1.2.1.1meet算子

現實空間中的對象求交最后往往轉換成對各個基本元素相交關系的判斷，包括點、線、面、圓等.通過組合可以實現空間維度擴張和收縮的外積和內積，以及可以表達對象正交補空間的對偶運算.共形幾何代數meet算子，在3D線性代數基礎上進行統一和擴展，可應用于n維空間的子空間求交[2].

Meet算子的計算借助于最小超空間和內積.最小超空間，即容納對象的最小空間在一個維度上的擴展.對于簡單多維對象，meet算子可以使用對象的偽標量來定義最小超空間，而對于復雜多維子空間對象，需要借助對象的join運算來定義對象的最小超空間[2,15].對于對象的join運算，這里不作展開.

(3)

式(3)中，對于簡單子空間對象，其代表A、B最小子空間的J可用A和B的偽標量I代替.

利用幾何代數meet算子可以對基本元素：點、線、面、圓的相交關系進行代數求解.其中，線線求交，兩直線異面或平行，其meet求解結果為無窮點，即兩直線相交于無窮點，也即不相交；直線與平面求交，直線和平面的管線有3種：相交、不相交、直線在平面上，需要對其meet結果和平方進行聯合判斷；面面求交，或平行或相交，根據其meet結果平方與0的比較結果來判斷[4].

表1 基本幾何元素的幾何代數meet求交計算

1.2.1.2 Half-space

幾何代數中基本幾何對象的meet求交，針對的對象是無邊界的、在其所在的維度子空間無限延伸的，而時空宗地卻是有明確權屬邊界的對象.將針對無限子空間的meet算子應用于有限幾何體的meet求交，則需要在幾何代數基本meet計算后，對meet結果的有效性進行判斷.

CAMERON等[16]在STOLFI等[17]提出的有向攝影幾何理論基礎上，對共形空間R3+1,1中各加1所表示的正、負空間(e+、e-)進行探討，提出了half-space(半空間)的概念.半空間是指用n-1維的實體A去分割n維實體B，以實體A為界，劃分B所在的空間的任一側空間，稱作半空間，其由一系列0維的點組成.例如：0維有向點分割1維直線空間，1維有向直線分割二維平面空間，2維有向平面分割3維體空間.在有向共形空間中，點、線、面、圓、球等都被賦予方向性，例如：A∧B∧n和B∧A∧n代表的是不同方向的2個直線對象，借鑒線和圓的Grassman層次結構的一致性，對代數所表達的直線方向的一致性進行判斷，可以將無窮點視作一個點，將線彎曲成圓，按同一方向排列的點的外積所表示的線對象是相等的，即為同一個對象，如圖3所示.半空間理論中引入求t值的表達式可以判斷兩直線方向的一致性.式(4)中，若表示的直線與所表示的直線方向一致，則t值大于0[16].

t=(A∧P∧n)(A∧B∧n).

(4)

圖3 方向一致性判斷Fig.3 The direction consistency judgement

1.2.2 時空宗地meet算子

在時空宗地meet算子中，對基本元素的交并關系求解，可通過幾何代數基本要素構建子空間(blade)直接參與meet求解[4].對于具有明確邊界約束的時空宗地，則先通過構建子空間參與基本meet運算后，對meet結果進行維度解析和對象解析.針對解析后的結果，通過有向共形幾何空間的半空間理論構建統一的算子，對meet的時空宗地進行meet有效性判斷.

時空宗地是在其所在空間中連續覆蓋不重疊的幾何體，時空宗地間原則上不存在相交的拓撲關系[9,14].近年來，由于土地資源過熱，時空宗地變更頻繁，且時空宗地間關系越來越復雜，則對時空宗地自身的演化進程以及演化過程中的鄰里關系進行研究顯得尤為重要.而這往往需要獲取時空宗地的歷史形態和歷史關聯.三維時空宗地是以宗地空間邊界多邊形為底、以生存時長為棱的平行多棱柱.在獲取時空宗地的歷史信息時，通過求解時空宗地平行多棱柱之間底面與頂面的meet關系，可以分析時空宗地的變更情況；通過求解時空切面與時空宗地的meet關系，可以獲取某一時空的土地利用現狀.

在進行以上2種meet場景求解時，需要先劃分時空宗地結構：時空近似體+時間線段+空間多邊形.時空近似體通過對空間近似對象在時間上進行均勻延伸構建.常見的空間近似對象有最小外包立方體、最小外包n邊平行棱柱和最小外包球3種.時空近似體的選取取決于時空對象的分布情況，根據其在時間和空間上的分布特征進行統計分析，以求取最佳時空近似體.例如，可借助“空間多邊形緊湊度”和“生存周期差異性”2個指標進行具體分析．本文選取最小外包球作為示例，對時空宗地的meet計算進行闡述.在此基礎上，可借助時空宗地最小外包球、時空宗地空間邊界多邊形和時空宗地時間棱，討論上述2種meet場景的求解.其中，球對象作為幾何代數的基本要素，可以直接使用幾何代數的meet算子進行求交，時空宗地空間邊界多邊形與時間棱線段對象則需要另作討論.據此，本文探討了半空間理論支持下的點與線段、點與多邊形、線段與線段、線段與多邊形、多邊形與多邊形的meet關系的求解，其中，點與線段和點與多邊形又是這5類對象meet求解的基礎.

表2 三維時空宗地meet場景討論

Table 2 Discussion on meet scene for three-dimensional spatio-temporal parcel

三維時空宗地meet場景三維時空宗地meet場景示意圖所需求解meet對象時空要素與時空宗地時間切面與時間棱：平面與直線、平面與線段時空宗地與時空宗地空間邊界與空間邊界：球與球、平面與平面、線段與線段、點與多邊形

1.2.2.1 點與線段、線段與線段

要判斷一個點對象P是否和一個線段對象meet，首先通過幾何代數meet求解點P和該線段所屬直線L的關系，若相交則表明點對象處于線段對象或線段對象延長線上.要進一步確定點對象是否和線段對象meet，需要利用線段的0維有向端點劃分1維直線的空間，構建表達式求解參數t值，判斷點處在哪一半空間.式(5)和(6)中，點在線段所在直線上，當(A∧P∧n)與L:(A∧B∧n)所表示的直線方向一致時，t1>0，當P點與A點重合時，t1=0，t2同t1.若不考慮點已在線段所在直線上的情況，圖4中t1和t2同時大于0表示的是一塊包含線段AB的二維區域，需要先將相交點P約束在一維線段AB之上，通過幾何代數基本元素的meet計算.

t1=(A∧P∧n)L,

(5)

t2=(P∧B∧n).

(6)

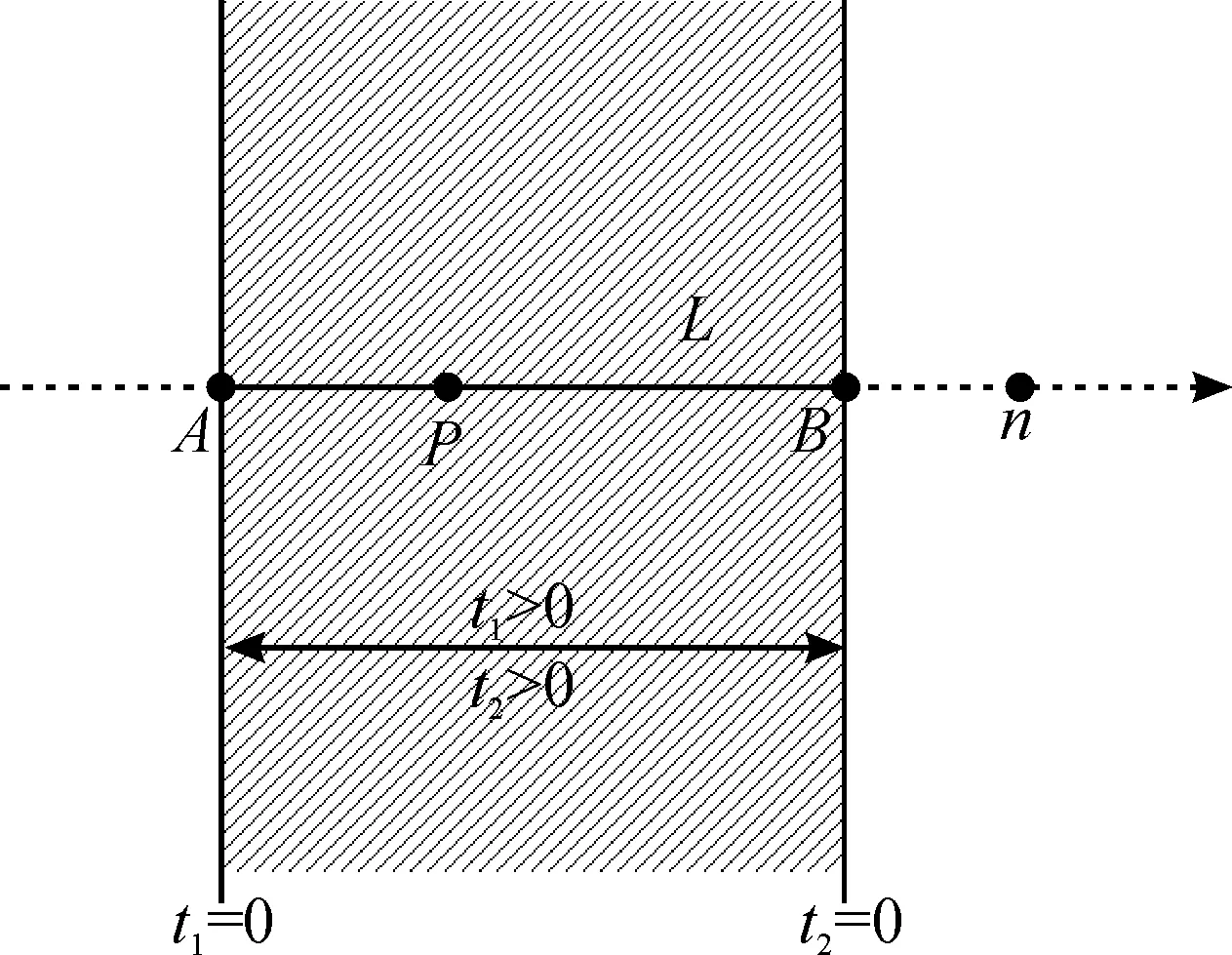
圖4 點P與線段AB的關系判斷Fig.4 Judgement of the relationship between thepoint P and the line segment AB

點與線段以及線段所在直線的相交關系可以分為：點與線段端點重合，點在線段上，點在線段延長線上.點不與線段所在直線相交也分為：點在直線左邊，點在直線右邊.要進一步確定點對象是否和線段對象相交，需要根據t1和t2判斷.如圖5所示，聯合κ值與t值進行判斷，可得到點與線段的相對關系.

結合圖5整理點與線段的關系，兩者之間可能存在的關系的推導過程見表3.

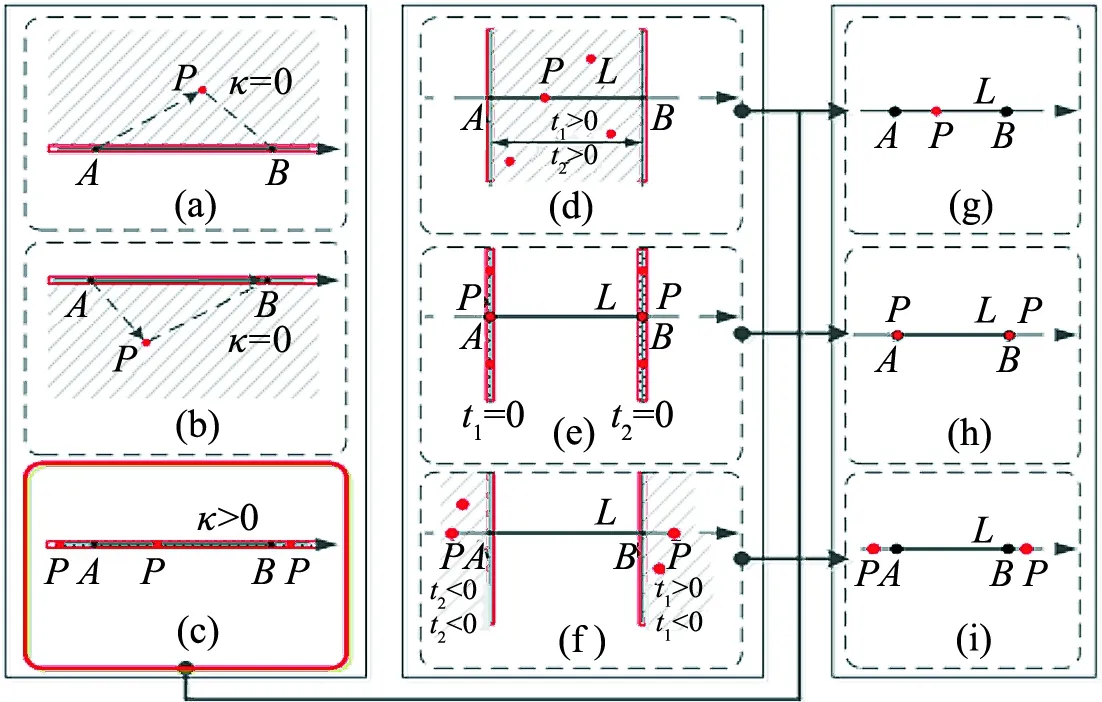
圖5 點P與線段AB的關系Fig.5 The relationship between the point P andthe line segment AB注 κ=grade((AI)(A∧B∧n)),t1=(A∧P∧n)(A∧B∧n),t2=(P∧B∧n)(A∧B∧n).

線段與線段的meet，用幾何代數meet排除平行和異面的情況后，基于點與線段的meet有效性判斷理論，判斷交點的有效性.交點P需要同時滿足與線段AB和CD的meet關系，見圖6，參考點與線段間的關系計算不再贅述.

1.2.2.2 點與多邊形、多邊形與多邊形

和零維有向點劃分一維線的半空間相同，一維有向線劃分出二維面的半空間.多邊形可以視作一系列有向線首尾相接形成的幾何圖形，多邊形所包絡的區域可以視作一系列有向直線劃分的平面半空間的交集.通過待求meet的點對象和多邊形有向邊界直線外積構成的有向面的方向，可以判斷該點對象是否與該多邊形對象圍成的區域meet.此外，基于點與多邊形、線段與線段的meet算子，可以構建多邊形之間的meet算子，見圖7.

表3 點與線段關系概況

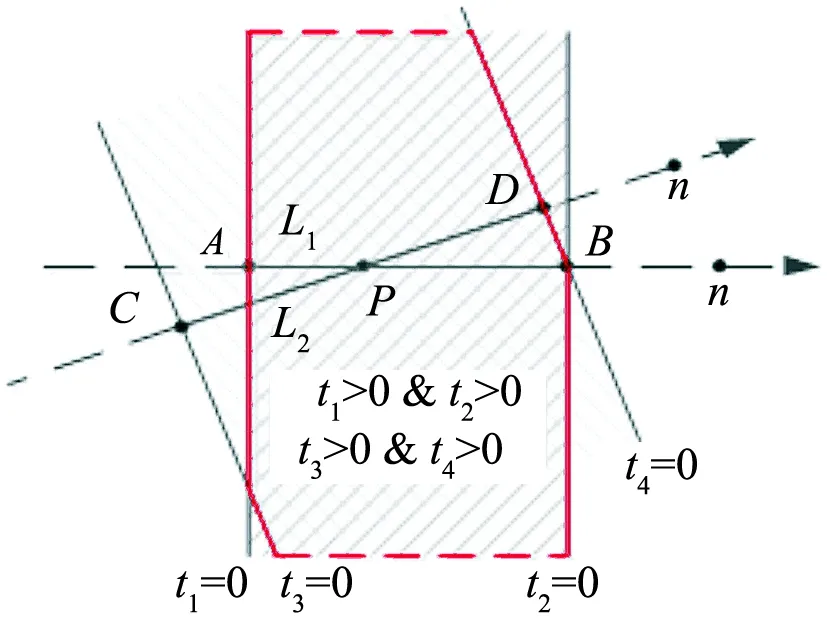
圖6 線段AB與CD關系的判斷Fig.6 Judgement of the relationship between the linesegment AB and the line segment CD

圖7 點P與多邊形ABCD關系判斷Fig.7 Judgement of the relationship betweenthe point P and the polygon ABCD

2 算法實現與案例驗證

2.1 算法描述與流程

時空宗地meet計算中基本共形幾何代數元素的meet可以直接使用共形幾何代數自帶meet算子進行求解，其中主要的具有邊界約束的幾何對象，則需在原meet算子基礎上引入有向半空間理論進行擴展.基于文中對時空宗地meet計算所做的闡述和討論，以三維時空宗地歷史回溯為例，對時空要素和三維時空宗地的meet進行求解，提出了具體的三維時空宗地meet算法流程.鑒于三維時空宗地和四維時空宗地表達形式的統一性，對于四維時空宗地的meet求解，只要在三維時空宗地構建的針對具有邊界約束的幾何對象的meet算子中，對點與多面體、多面體與多面體的meet求解再進行具體討論，構建相關的meet算子即可.三維時空宗地歷史回溯meet算法流程如圖8所示.

對三維時空宗地的歷史回溯meet算法步驟如下：

(1)對輸入的時空宗地使用共形幾何代數進行編碼轉換，對輸入的觀測時間(回溯時間)使用幾何代數外積構建時間切面S;

(2)按一定組織順序遍歷時空宗地集合中的所有時空宗地對象;

(3)判斷時空切面與時空宗地最小外包球MBC是否meet;

(4)若meet，判斷時間切面與時空宗地的任一時間棱L是否meet:

1)求解時間切面S與時間棱L所在直線C的meet關系，得到meet結果M；

2)若S與Cmeet，對M進行維度解析和對象解析，提取交點信息；

3)使用有向半空間Omeet求解交點對于時間棱線段L的有效性.若相交，則將時空宗地的空間邊界正射投影于時間切面并輸出結果.

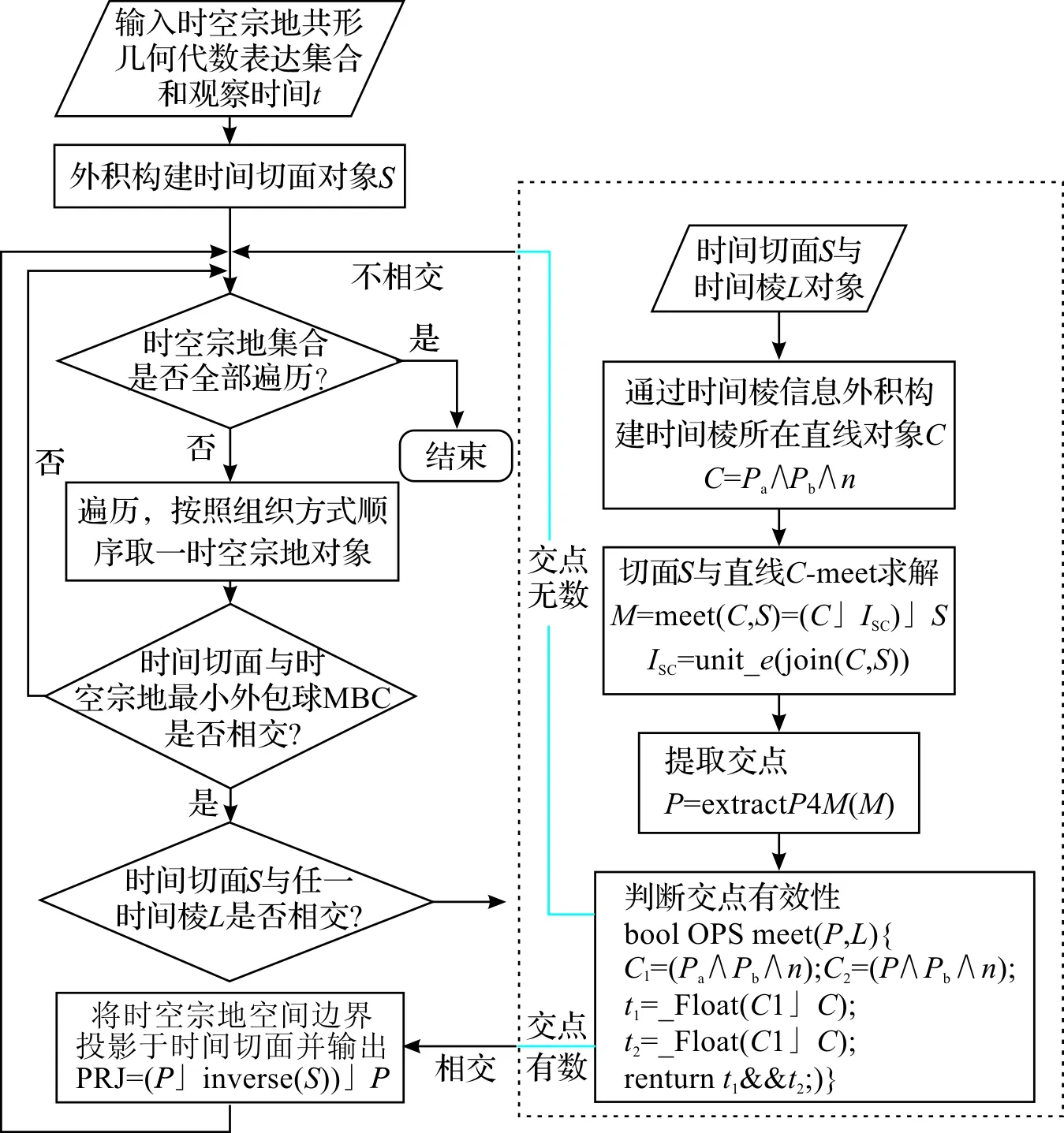
圖8 基于meet計算的三維時空宗地歷史回溯場景求解Fig.8 The history tracebacking scene resolution of three dimensionalspatio-temporal parcel based on meet computation

2.2 案例驗證

以杭州建德市新安江鎮白沙村自20世紀90年代登記以來的地籍數據為例進行算法驗證，分別選取1996年1月1日、2002年1月1日、2006年1月1日、2010年1月1日為時間節點，構建時間掃描面，與時空宗地meet求交. 圖 9(a)中展示的是軸構建的時空中三維時空宗地的形態，即宗地在時間維度上展開，圖 9(b)、(c)、(d)展示了時間切面按一定時間采樣間隔構建掃描面，與時空宗地進行meet計算的動態過程：圖9(b)為2002年1月1日的時間切面與時空宗地meet計算的結果，反映了2002年1月1日的宗地現狀；圖9(c)為2006年1月1日的時間切面與時空宗地meet計算的結果，反映了2006年1月1日的宗地現狀；圖9(d)為2010年1月1日的時間切面與時空宗地meet計算的結果，反映了2010年1月1日的宗地現狀.圖9(b)、(c)、(d)中，不同顏色的多棱柱分別代表不同類型的土地用途，藍紫色平面為時間掃描面，突出顯示的紅色多邊形為時間掃描面和時空宗地meet求交的結果.相應地，圖10中的(a)、(b)、(c)、(d)分別為在ArcGIS平臺上進行渲染的1996年1月1日、2002年1月1日、2006年1月1日、2010年1月1日的實際宗地確權狀況.

將求交結果與現實登記中宗地確權結果相比較，即圖9與圖10的比較.結果顯示，基于時空宗地meet算子計算的歷史節點上的宗地確權結果與實際宗地確權結果吻合，說明基于幾何代數理論構建的時空宗地meet計算流程,能夠較好地應用于宗地時空拓撲的計算.

本文通過案例驗證了基于幾何代數的三維時空宗地表達和meet計算的可行性，同時，為四維時空宗地的幾何代數表達和拓撲計算提供了時空宗地表達模型以及拓撲meet算子構建的理論基礎和研究思路.

圖9 基于時空宗地meet算子的時間掃描面與時空宗地求交Fig.9 The meet computation between time sweep planeand spatio-temporal parcel based on meet operator

圖10 實際宗地確權結果Fig.10 The parcel registration results

3 結論與展望

處于地理世界中的物體具有很強的時空依賴性和動態性，時空作為物體的固有屬性，對其變化過程的研究具有重要意義.目前，對于時空變化過程的研究多基于關系數據庫檢索，此方法受限于數據庫的表達和檢索的水平.本文在現有時空宗地數據模型研究的基礎上，對幾何代數的時空表達、交并計算、有向半空間劃分等內容展開了研究，利用幾何代數多維統一、高維計算適應的優勢，設計了基于幾何代數meet算子和有向半空間劃分理論的時空宗地meet算法.并探討了時空宗地變化過程中的2種meet場景，針對時空宗地meet場景涉及的時空宗地最小外包球、時空宗地空間邊界多邊形、時空宗地時間棱的meet求解展開了具體的討論，最后從三維時空宗地歷史回溯角度出發，設計了三維時空歷史回溯的meet算法.實驗證明，該meet算法能在脫離傳統關系數據庫查找的模式下，較好地滿足歷史回溯和時空變化過程可視化展示的需求，相比于傳統方法，不受限于關系數據庫的表達和檢索能力，更加靈活，且易擴展.該算法的理念同樣適用于四維時空宗地的歷史回溯meet求解.據此，后續的重點工作主要為:對四維時空宗地的幾何結構組成要素(多面體)的meet計算進行擴展，對時空超平面等四維時空基本元素的特性進行理解和表達，對三維、四維時空宗地同時存在的多維混合時空meet進行擴展.

[1] 李洪波.共形幾何代數——幾何代數的新理論和計算框架[J].計算機輔助設計與圖形學學報，2005,17(11):2383-2393. LI H B. Conformal geometric algebra-A new framework for computational geometry[J]. Journal of Computer Aided Design & Computer Graphics,2005,17(11):2383-2393.

[2] DORST L, FONTIJNE D, MANN S. Geometric Algebra for Computer Science: An Object-Oriented Approach to Geometry[M]. San Francisco: Morgan Kaufmann Publishers Inc,2007.

[3] 羅文,袁林旺,俞肇元,等.基于共形幾何代數的三維地理場景建模與表達[J].測繪通報,2012(10):28-31. LUO W, YUAN L W, YU Z Y, et al. Conformal geometric algebra-based three dimensional scene modeling and expressing [J]. Bulletin of Surveying and Mapping,2012(10):28-31.

[4] 宗真,袁林旺,羅文,等.三角網求交的共形幾何代數算法[J].測繪學報,2014(2):200-207. ZONG Z, YUAN L W, LUO W, et al. Triangulation intersection algorithm based on conformal geometric algebra [J]. Acta Geodaetica et Cartographica Sinica,2014(2):200-207.

[5] D?NER F, THOMPSON R, STOTER J, et al. 4D cadastres: First analysis of legal, organizational and technical impact - With a case study on utility networks[J]. Land Use Policy,2010,27(4):1068-1081.

[6] D?NER F, THOMPSON R, STOTER J, et al. Solutions for 4D cadastre - with a case study on utility networks[J]. International Journal of Geographical Information Science,2011,25(7):1173-1189.

[7] SONG W, YANG X. A spatio-temporal cadastral data model based on space-time composite model[C]// International Conference on Geoinformatics. Kaifeng: IEEE,2013:1-4.

[8] CLARAMUNT C, JIANG B. An integrated representation of spatial and temporal relationships between evolving regions[J]. Journal of Geographical Systems,2001,3(4):411-428.

[9] 史云飛,郭仁忠,李霖,等.四維地籍的建立與分析[J].武漢大學學報：信息科學版,2014,39(3):322-326. SHI Y F, GUO R Z, LI L, et al. Establishment and analysis 4D cadastre[J]. Geomatics and Information Science of Wuhan University,2014,39(3):322-326.

[10] 俞肇元,袁林旺,胡勇,等.基于幾何代數的矢量時空數據表達與建模方法[J].地球信息科學學報,2012,14(1):67-73. YU Z Y,YUAN L W, HU Y, et al. Spatio-temporal vector data modeling based on geometric algebra[J].Journal of Geo-Information Science,2012,14(1):67-73.

[11] HESTENES D. Space-Time Algebra[M]. Switzerland: Springer International Publishing,1966.

[12] 李武明,張雪峰.時空平面的Clifford代數與Abel復數系統[J].吉林大學學報：理學版,2007,45(5):748-752. LI W M, ZHANG X F. Clifford algebra of spacetime plane and Abel complex number system[J]. Journal of Jilin University: Science Edition,2007,45(5):748-752.

[13] 李武明.時空代數的若干性質及應用[J].通化師范學院學報,2004,25(8):1-3. LI W M. The properties and application of the space time algebra[J]. Journal of Tonghua Teachers College,2004,25(8):1-3.

[14] 張玲玲,史云飛,郭仁忠,等.三維地籍產權體的定義與表達[J].地球信息科學學報,2010,12(2):207-213. ZHANG L L, SHI Y F, GUO R Z, et al. Definition and representation of property volume of three dimensional cadastre[J]. Journal of Geo-Information Science,2010,12(2):207-213.

[15] 袁林旺.基于幾何代數的多維統一GIS[M].北京：科學出版社,2012. YUAN L W. Multi-dimensional Unified GIS Base on Geometric Algebra [M].Beijing：Science Press,2012.

[16] CAMERON J, LASENBY J. Oriented conformal geometric algebra[J]. Advances in Applied Clifford Algebras,2008,18(3/4):523-538.

[17] STOLFI J. Oriented Projective Geometry: A Framework for Geometric Computations[M]. Boston: Academic Press,1991.

WANG Qiaoyan1,2, JIANG Xiaomin1,2, ZHANG Feng1,2, DU Zhenhong1,2, LIU Renyi1,2

(1.ZhejiangProvincialKeyLaboratoryofResourcesandEnvironmentalInformationSystem,ZhejiangUniversity,Hangzhou310028,China; 2.DepartmentofEarthSciences,ZhejiangUniversity,Hangzhou310027,China)

Geometric algebra has advantages in solving problems of geometric object modeling and multidimensional data analysis. This paper conducts studies on the meaning, construction and application of its two operators: meet and join. By exploiting their merits of multidimensional consistency and high dimension adaptivity, we propose a spatio-temporal parcel meet algorithm. We also give definitions and representations of 3D and 4D spatio-temporal parcel within the domain of conformal geometric algebra and spatio-temporal algebra. The algorithm is successfully applied to conduct the topology computation of three dimension spatio-temporal parcels and achieves satisfactory results. . Experiment show that our approach provides a novel and effective way for the representation and topology computation of three dimensional spatio-temporal parcel and hopefully a new resolution for four dimensional spatio-temporal parcels.

geometric algebra; spatio-temporal topology relation computation; meet operator; spatio-temporal parcel meet

2016-01-05.

國家自然科學基金資助項目(41471313,41101356,41101371,41171321)；國家科技基礎性工作專項(2012FY112300)；海洋公益性行業科研專項經費資助(2015418003,201305012)；浙江省攻關項目(2014C33G20,2013C33051).

王巧燕(1991-)，ORCID:http://orcid.org/0000-0002-5636-8184,女，碩士研究生，主要從事時空數據建模研究，E-mail:qywangZJUGIS@163.com.

*通信作者，ORCID:http://orcid:org/0000-0003-1475-8480,E-mail:zfcarnation@zju.edu.cn.

10.3785/j.issn.1008-9497.2017.01.012

P208

A

1008-9497(2017)01-076-08