不同設防標準RC框架結構 基于易損性分析的抗震性能評估1

徐 超 溫增平

?

不同設防標準RC框架結構 基于易損性分析的抗震性能評估1

徐 超 溫增平

（中國地震局地球物理研究所，北京 100081）

借助非線性動力時程分析，對嚴格按照規范Ⅶ、Ⅷ、Ⅸ度設計的5個三跨6層鋼筋混凝土框架結構開展易損性分析，建立了基于峰值加速度的易損性曲線。從易損性的角度對不同設防標準RC框架結構的抗震性能做了定量評價，并探討了設防標準對RC框架結構易損性的影響。分析表明，對應于設防小震、中震及大震水平的峰值加速度，結構“小震不壞”、“中震可修”和“大震不倒”的失效概率均在18%以內，可認為結構滿足三水準的性態控制目標。隨著結構設防標準的提高，其易損性隨之降低，相同峰值加速度對應的各個破壞狀態的超越概率均有所降低。此外，將框架結構的設防烈度提高1度，其“大震不倒”的失效概率會明顯減小。而將框架結構的設防烈度降低1度，其“大震不倒”的失效概率會顯著增加，最高可達4倍。

地震易損性 抗震性能 非線性動力時程分析 抗震設防標準 RC框架結構

引言

房屋等建筑物的倒塌和嚴重破壞，是造成地震人員傷亡和財產損失的主要原因。提高建筑物的抗震性能是減少損失的有效途徑。抗震設防烈度（設計基本地震加速度）是控制房屋建筑抗震性能的重要參數。我國建筑抗震設計規范（GB50011—2010）（中國建筑科學研究院，2015）將建筑物的抗震設防烈度（設計基本地震加速度）分為Ⅵ度（0.05g）、Ⅶ度（0.1g，0.15g）、Ⅷ度（0.2g，0.3g）和Ⅸ度（0.4g）6檔，依此進行結構抗震設計。按照不同抗震設防烈度設計的房屋，其抗震性能如何，以及抗震設防烈度對房屋的抗震性能有何影響是值得深入探討的問題。本文以RC框架結構為對象，以結構易損性為切入點對不同設防標準結構的抗震性能做了定量評價，并探討了設防標準對結構易損性的影響。基于非線性動力時程分析，對嚴格按照規范Ⅶ度（0.1g）、Ⅶ度（0.15g）、Ⅷ度（0.2g）、Ⅷ度（0.3g）和Ⅸ度（0.4g）設計的5個三跨6層鋼筋混凝土框架結構開展易損性分析，建立了以地震動峰值加速度作為輸入參數的易損性曲線。根據不同水準地震作用下結構各個破壞狀態的超越概率，對結構“小震不壞”、“中震可修”及“大震不倒”性態控制目標的實現情況進行了識別。通過比較結構不同破壞狀態的超越概率曲線以及“大震不倒”性態控制目標的失效概率，研究了設防標準對RC框架結構抗震性能的影響。研究工作對于完善房屋建筑抗震設計有一定參考意義。

1 基于地震動參數的易損性分析

1.1 易損性模型

結構易損性表示在給定強度水平的地震動作用下，結構超越一定破壞狀態的條件概率，其概率表達形式如下：

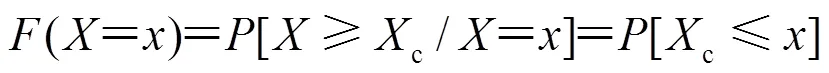
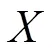
研究表明（尹之潛，1995；Singhal等，1996；Song等，1999；Shinozuka等，2000），對數正態分布是較理想的易損性概率模型，即隨機變量c服從對數正態分布。易損性可進一步表述為：

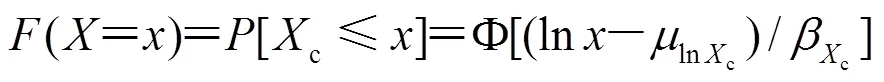
根據對數正態分布的性質，自然對數的均值等于中值的自然對數，上式可寫成：

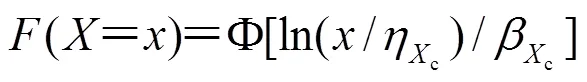
1.2 易損性分析方法

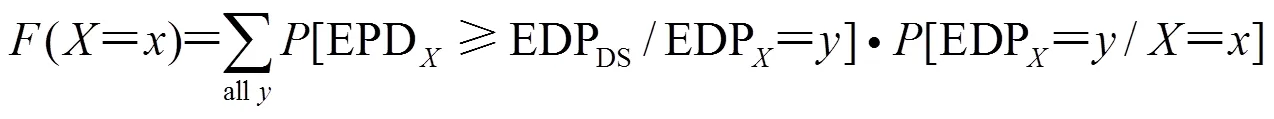
1.2.1 結構概率地震需求模型

在給定強度水平的地震動作用下的結構最大層間位移角反應服從對數正態分布（Shome，1999）。因此，結構概率地震需求模型，也即結構的最大層間位移角與地震動參數PGA的統計關系為：

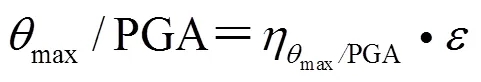
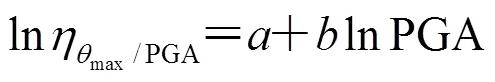
圖1 概率地震需求模型

1.2.2 結構破壞準則

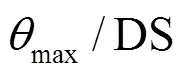
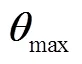
表1 不同破壞狀態對應最大層間位移角的統計參數

1.2.3 易損性計算

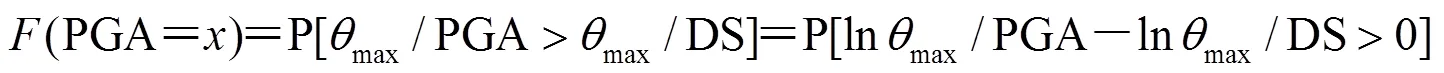
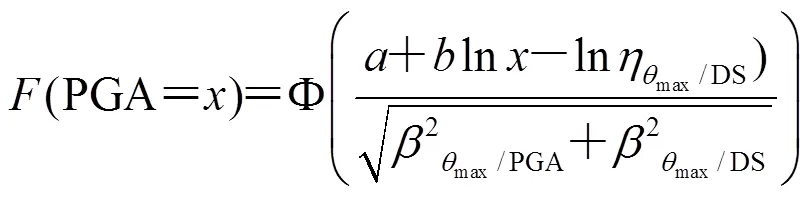
2 不同設防標準RC框架結構的易損性

2.1 結構設計及建模

根據二類場地、第一設計地震動分組，按照抗震設計規范（GB50011—2010）（中國建筑科學研究院，2015）Ⅶ度（0.1g）、Ⅶ度（0.15g）、Ⅷ度（0.2g）、Ⅷ度（0.3g）和Ⅸ度（0.4g）設計5個6層規則鋼筋混凝土框架結構，結構的平立面簡圖如圖2所示。現澆樓板厚100mm，屋面板厚120mm；樓面恒載取4.0，樓面活荷載取2.5，屋面恒載取7.0，填充墻折算為9的梁上線荷載。梁、柱主筋采用HRB335鋼筋，混凝土強度等級C30。

考慮到結構布置規則對稱，在每一個框架結構中選取一榀框架進行分析。采用Drain-2DX程序建立平面彈塑性地震反應分析模型（Prakash等，1993）。采用帶塑性鉸的梁-柱非線性單元模擬梁柱構件，非線性單元的彎矩曲率滯回曲線采用不考慮剛度退化的雙線性模型，應變硬化比為2%。考慮現澆樓板對框架梁的剛度及抗彎承載力的影響，將框架梁以矩形截面計算的剛度及反向抗彎承載力分別提高50%和20%（吳勇等，2002；王振波等，2015）。通過模態分析可得結構的基本自振周期分別為1.13s、1.1s、0.9s、0.7s和0.62s。

2.2 地震動輸入的選取

地震動的不確定性是易損性分析中不確定性的主要來源。相比于地震動的不確定性，結構模型不確定性的影響很小，因此本文在分析中僅考慮地震動不確定性的影響。從PEER強震數據庫（http://peer. berkeley.edu/nga）中選取一系列加速度記錄作為非線性動力分析的輸入，以“記錄對記錄”的變異性來體現地震動不確定性的影響。為了使輸入地震動具有一般性，選擇加速度記錄時盡量覆蓋較寬的震級和距離范圍，且記錄中不包含明顯的速度脈沖特征。最終選擇的90條加速度記錄的基本信息如表2所示。

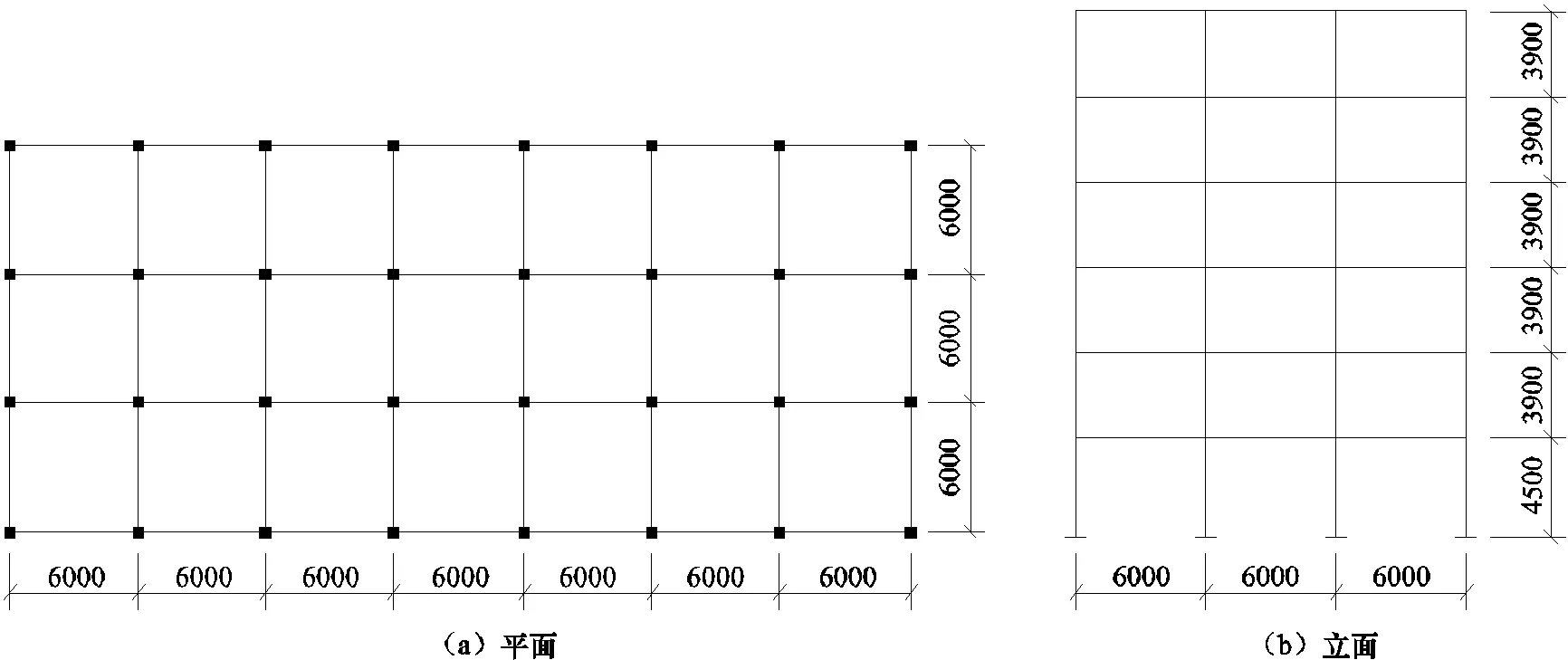
圖2 結構平立面簡圖

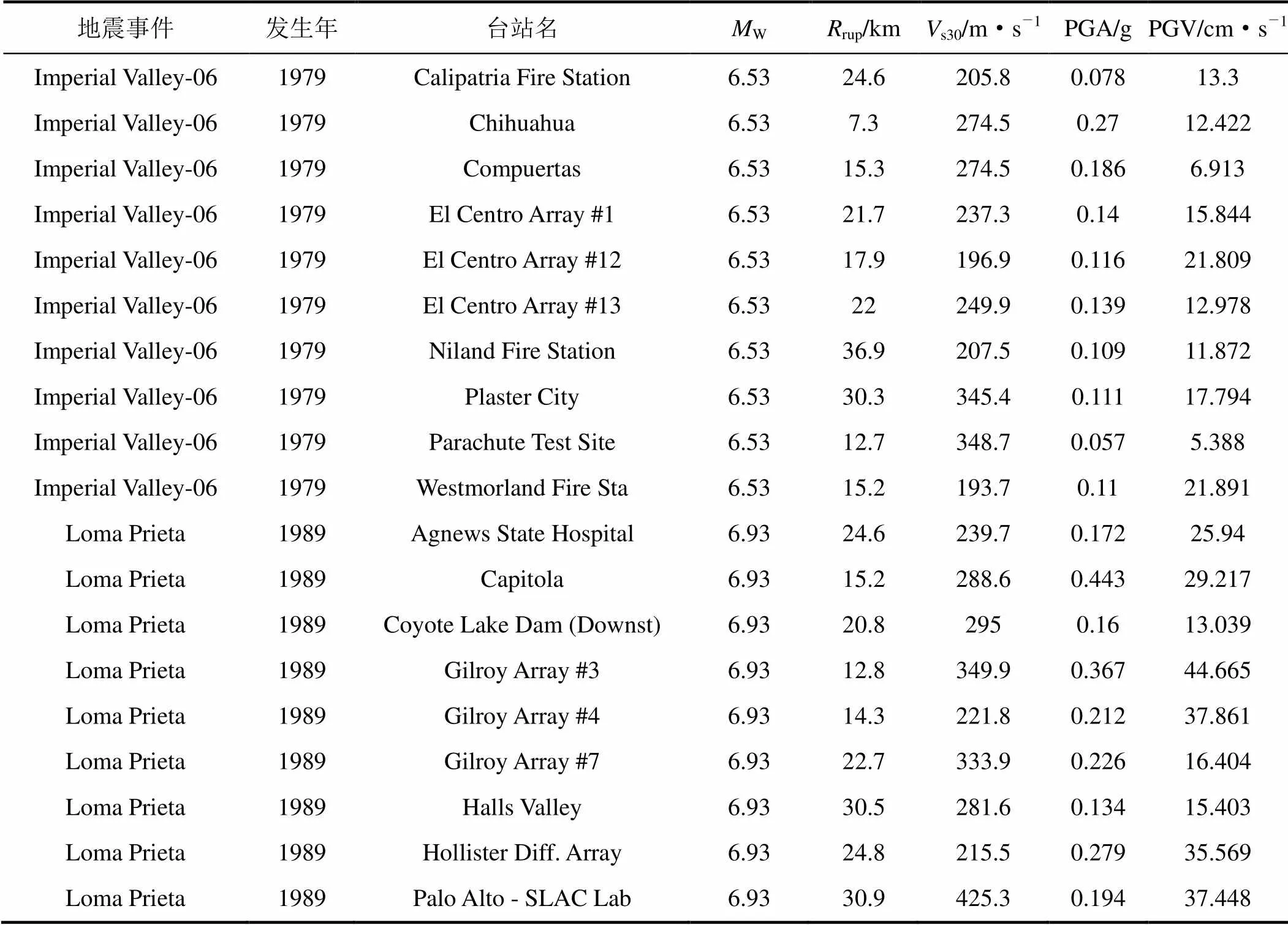
表2 輸入地震動記錄的基本信息

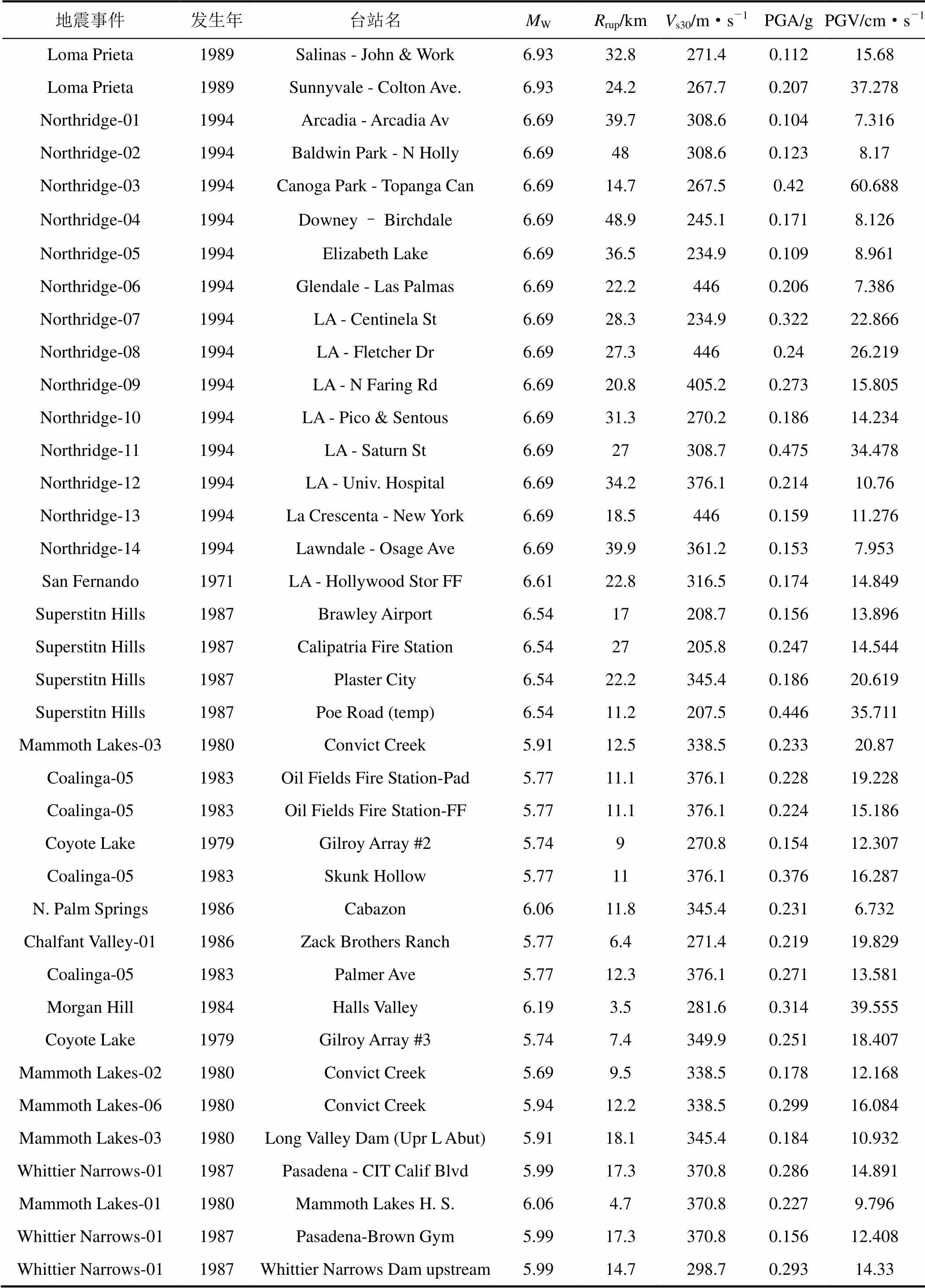
續表

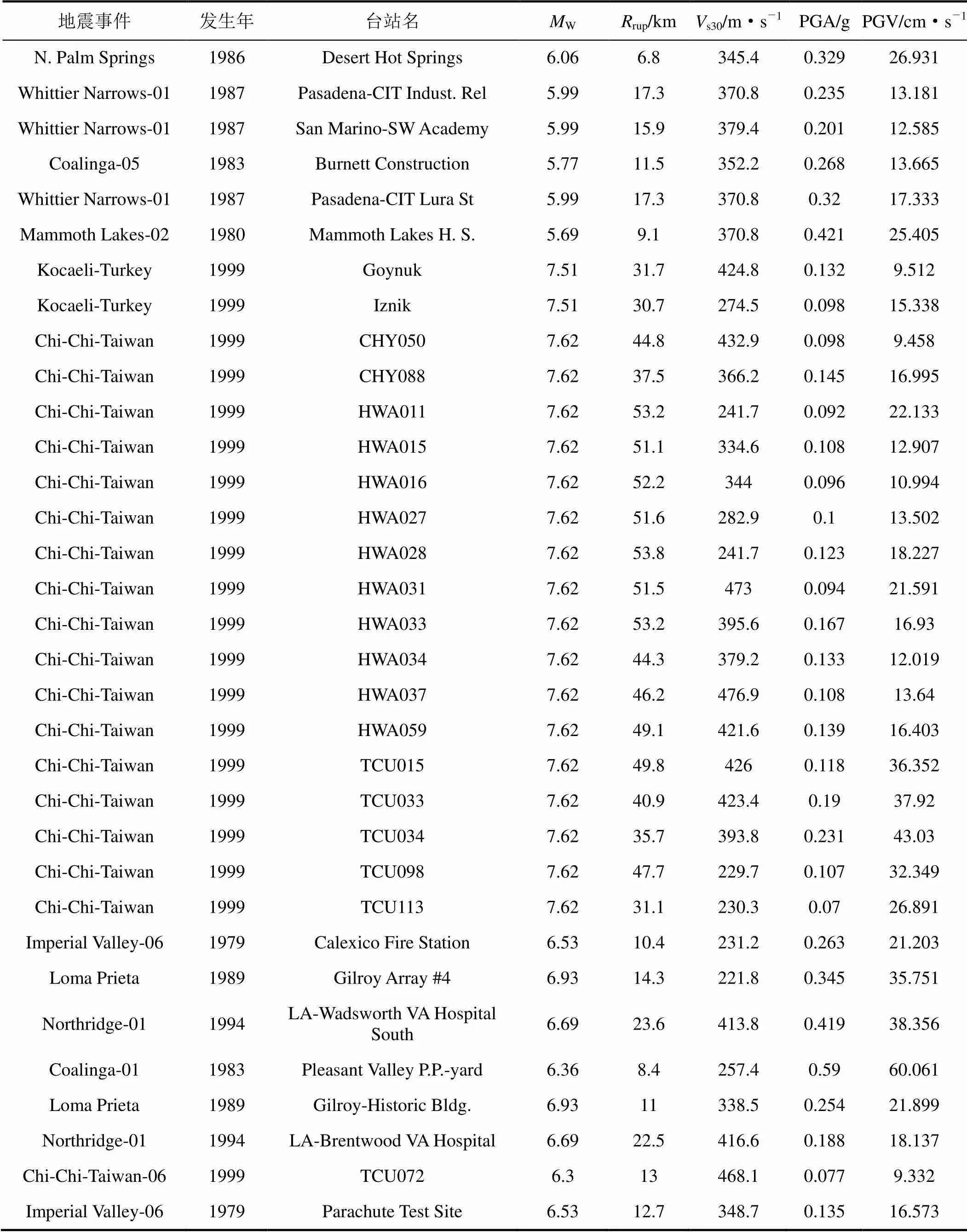
續表

2.3 易損性分析結果

所選擇的90條加速度作為輸入分別對5個框架結構開展非線性動力時程分析，基于最大層間位移角與峰值加速度的回歸擬合確定結構的概率地震需求模型如下：

基于以上結構概率地震需求模型和表1的結構破壞準則，根據式（8）可分別計算5個不同設防水準框架結構的易損性，圖3為5個不同設防水準框架結構基于峰值加速度的易損性曲線。

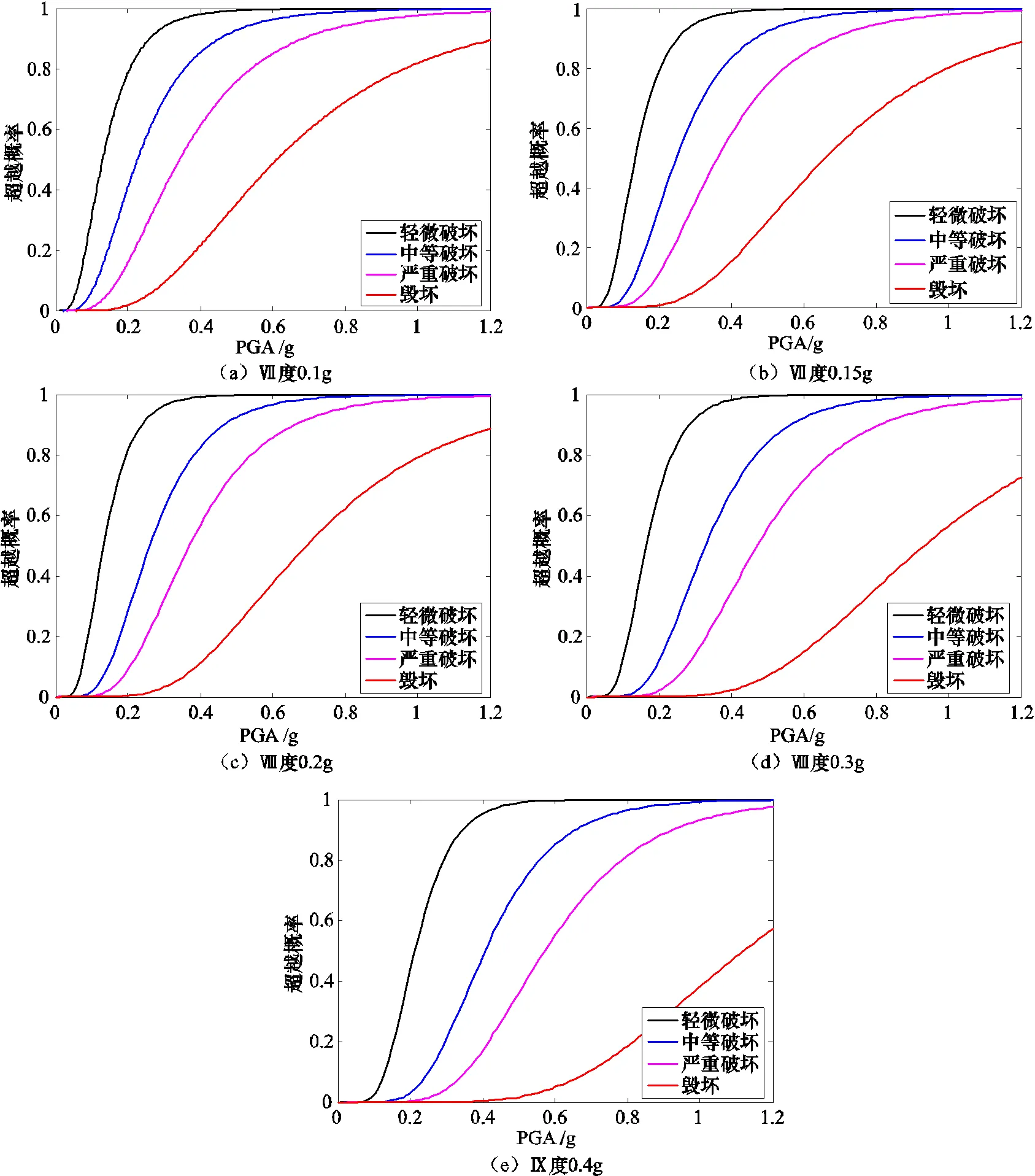
圖3 不同設防標準框架結構基于峰值加速度的易損性曲線

3 設防標準對結構抗震性能的影響

3.1 三水準性態控制目標的識別

根據框架結構的易損性曲線可以得到不同水準地震峰值加速度對應的各破壞狀態的超越概率。表3列出了在不同設防烈度標準下，小震、中震及大震水準對應的峰值加速度值。表4為不同設防標準框架結構對應于小震、中震及大震水準峰值加速度的各個破壞狀態的超越概率。一般認為在結構的破壞狀態中，“基本完好”狀態對應于“不壞”的性態控制目標，“中等破壞”狀態及以下對應于“可修”的性態控制目標，“嚴重破壞”狀態及以下對應于“不倒”的性態控制目標。由此可得各框架結構“小震不壞”、“中震可修”及“大震不倒”性態控制目標的失效概率（表5）。可以看出，Ⅶ度0.1g、Ⅶ度0.15g及Ⅷ度0.2g設防框架結構三水準性態控制目標的失效概率基本都在12%以內，Ⅷ度0.3g和Ⅸ度0.4g設防框架結構三水準性態控制目標的失效概率都在15%左右，總體而言可認為這些不同設防標準的框架結構滿足“小震不壞”、“中震可修”及“大震不倒”的三水準性態控制目標。從表中還可以看出，低設防標準如Ⅶ度0.1g和Ⅶ度0.15g的框架，其三水準性態控制目標的失效概率相比高設防標準框架結構的失效概率更低，這可能是由于低設防標準框架結構的承載力設計由非地震荷載控制所致。

表3 小震、中震及大震對應的峰值加速度（單位：g）

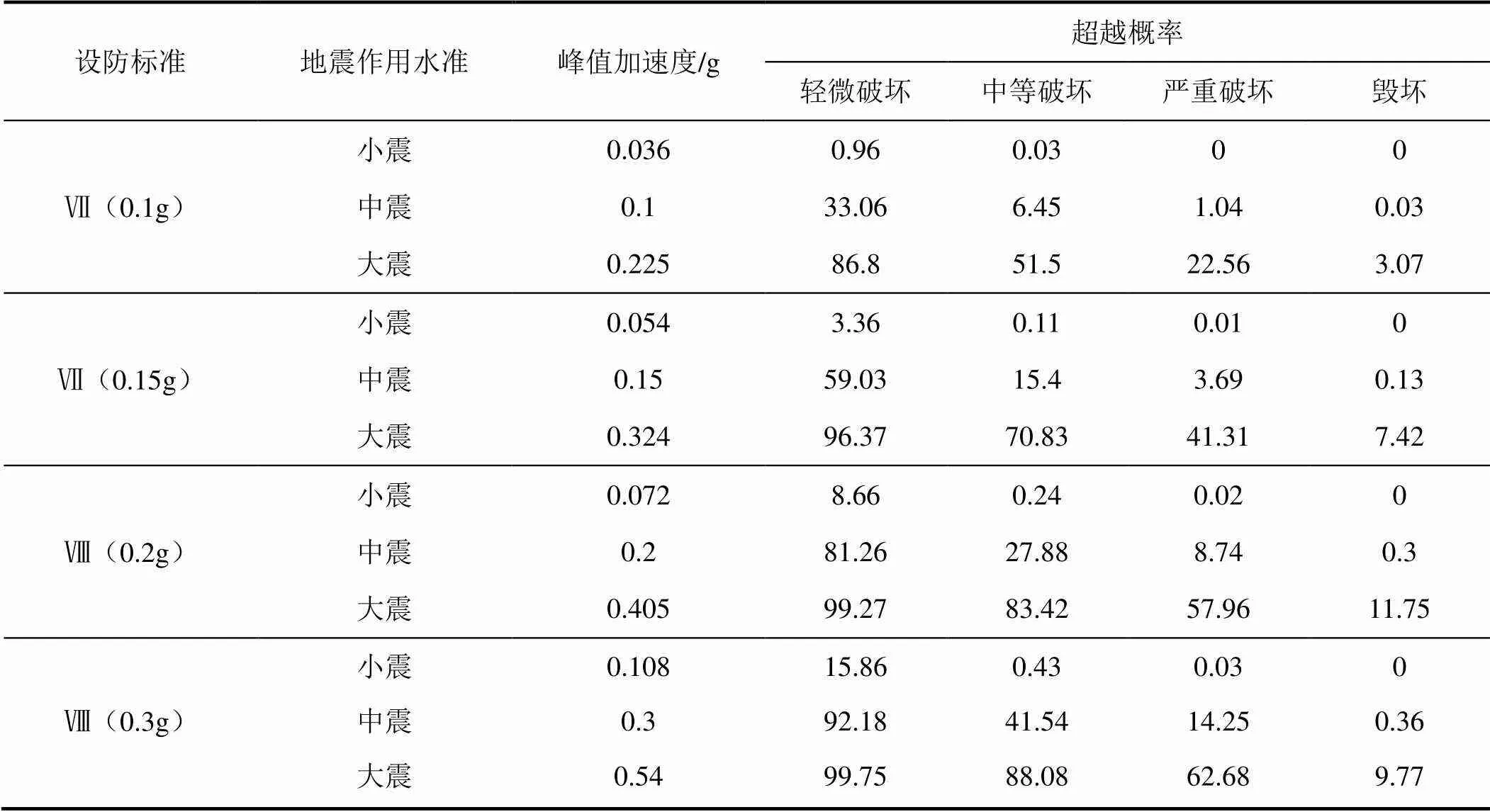
表4 小震、中震及大震水準地震作用下結構各個破壞狀態的超越概率

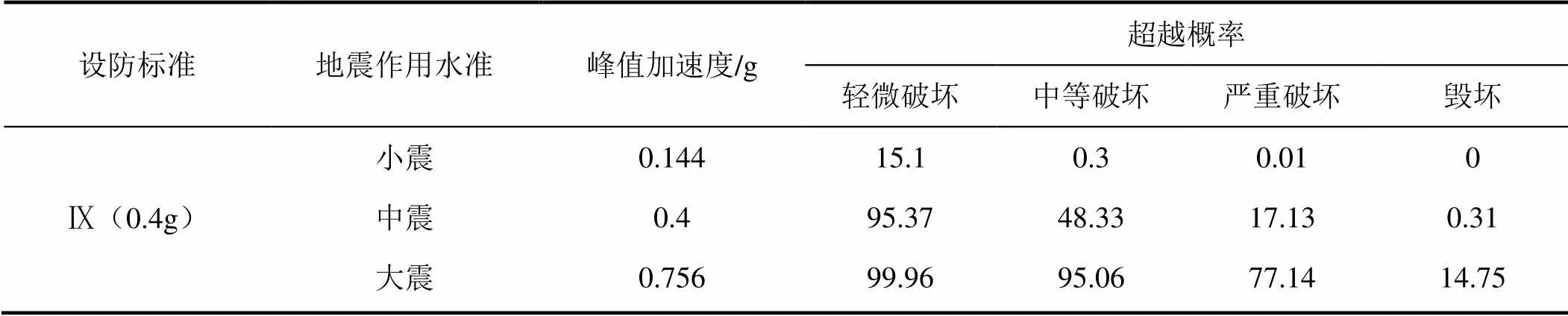
續表

表5 結構三水準性態控制目標的失效概率

3.2 不同設防標準結構抗震性能的比較

為了直觀地比較不同設防水準框架結構的易損性，圖4分別給出了結構不同破壞狀態基于峰值加速度的超越概率曲線。可以看出，隨著設防標準的提高，結構抗震性能隨之提高，其易損性也明顯降低，特別是Ⅷ度0.3g框架和Ⅸ度0.4g框架易損性的降低尤為顯著。具體表現為設防標準越高，相同峰值加速度對應各個破壞狀態的超越概率越低。根據易損性曲線可計算不同設防標準框架結構對應于Ⅶ—Ⅸ度大震水準峰值加速度的倒塌概率，如表6所示。該表體現了提高或者降低結構的設防標準對其“大震不倒”失效概率的影響。從表中可以看出，如果將Ⅶ度0.1g區框架的設防標準提高1度至Ⅶ度0.2g，其大震倒塌概率由3.07%降至0.65%；將Ⅶ度0.15g區框架的設防標準提高1度至Ⅷ度0.3g，其大震倒塌概率由7.42%降至0.61%；將Ⅷ度0.2g區框架的設防標準提高1度至Ⅸ度0.4g，其大震倒塌概率由11.75%降至0.34%。相反，如果將Ⅸ度0.4g區框架的設防標準降低1度至Ⅷ度0.2g，其大震倒塌概率由14.75%升至57.55%；將Ⅷ度0.3g區框架的設防標準降低1度至Ⅶ度0.15g，其大震倒塌概率由9.76%升至34.26%；將Ⅷ度0.2g區框架的設防標準降低1度至Ⅶ度0.1g，其大震倒塌概率由11.75%升至22.87%。綜合而言，如果將框架結構實際設防烈度在規范抗震設防烈度的基礎上提高1度，其“大震不倒”的失效概率會明顯減小。而將框架結構的實際設防烈度在規范抗震設防烈度的基礎上降低1度，則其“大震不倒”的失效概率會顯著增加，甚至可達4倍之多，這種風險值得重視。

表6 大震峰值加速度對應的結構的倒塌概率（%）

續表

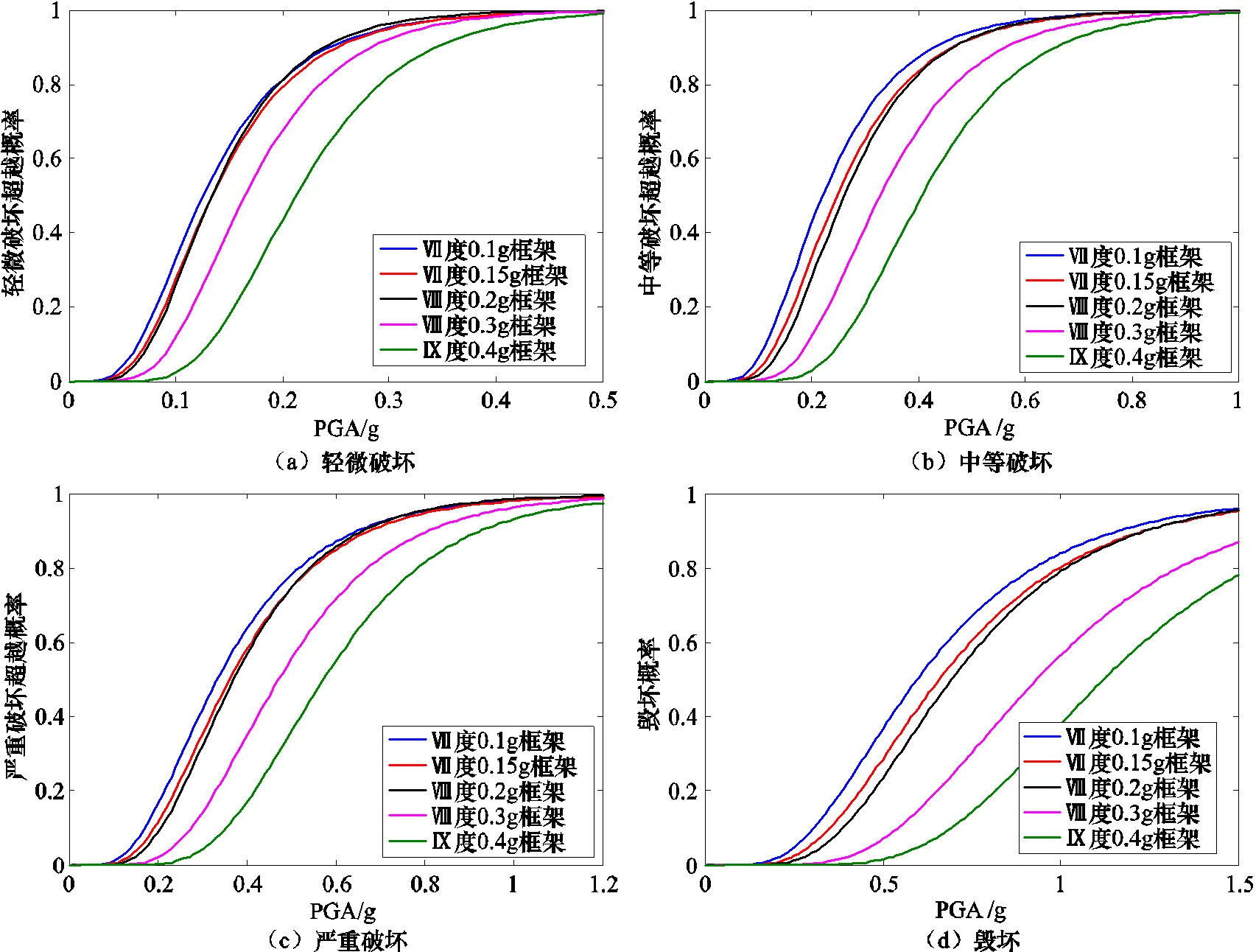
圖4 不同設防標準框架結構易損性曲線的比較

4 結論

通過對不同設防水準的RC框架結構開展易損性分析及抗震性能評估，得到以下結論：

（1）Ⅶ度0.1g、Ⅶ度0.15g及Ⅷ度0.2g設防框架結構三水準性態控制目標的失效概率最高在10%左右，Ⅷ度0.3g和Ⅸ度0.4g設防框架結構三水準性態控制目標的失效概率最高在15%左右，總體可認為5個框架均滿足“小震不壞”、“中震可修”及“大震不倒”的性能目標。

（2）隨著設防標準的提高，結構抗震性能隨之提高，其易損性也明顯降低，特別是Ⅷ度0.3g框架和Ⅸ度0.4g框架易損性的降低尤為顯著。具體表現為設防烈度越高，易損性曲線上相同峰值加速度對應各個破壞狀態的超越概率越低。

（3）如果將框架結構實際設防烈度在規范抗震設防烈度的基礎上提高1度，其“大震不倒”的失效概率會明顯減小。而將框架結構的實際設防烈度在規范抗震設防烈度的基礎上降低1度，則其“大震不倒”的失效概率會顯著增加，甚至可達4倍之多，這種風險不容忽視。

高小旺，沈聚敏，1993a．“大震”作用下鋼筋混凝土框架房屋變形能力的抗震可靠度分析．土木工程學報，26（3）：3—12．

高小旺，沈聚敏，1993b．鋼筋混凝土框架房屋不同破壞狀態的抗震可靠度分析．建筑科學，9（1）：3—11．

高小旺，沈聚敏，1993c．鋼筋砼框架結構層間極限變形能力的簡化計算方法．建筑結構學報，14（2）：28—38．

高小旺，邵卓民，1996．鋼筋混凝土房屋變形能力的抗震可靠度分析．“災害作用和結構抗災可靠度標準研究”一九九六年度研究報告．中國建筑科學研究院工程抗震研究所，建設部標準定額研究所．

王振波，解子林，2015．現澆板對RC框架結構抗震性能影響的試驗研究．震災防御技術，10（4）：979—985．

吳勇，雷汲川，楊紅等，2002．板筋參與梁端負彎矩承載力問題的探討．重慶建筑大學學報，24（3）：33—37．

尹之潛，1995．地震災害及損失預測方法．北京：地震出版社．

中國建筑科學研究院，2010．建筑抗震設計規范（GB 50011—2010）．北京：中國建筑工業出版社．

鐘益村，王文基，田家驊，1984．鋼筋混凝土結構房屋變形性能及容許變形指標．建筑結構，（2）：38—45．

PEER ground motion database. http://peer.berkeley.edu/nga.

Prakash V., Powell G. H., Campbell S., 1993. DRAIN-2DX: basic program description and user guide. Report No. UBC/SEMM-93/17. Berkeley: University of California at Berkeley.

Shinozuka M., Feng M. Q., Lee J, et al., 2000. Statistical analysis of fragility curves. Journal of Engineering Mechanics, 126(12): 1224—1234.

Shome N., 1999. Probabilistic seismic demand analysis of nonlinear structures. Stanford: Stanford University.

Singhal A., Kiremidjian A. S., 1996. Method for probabilistic evaluation of seismic structural damage. Journal of Structural Engineering, 122(12): 1459—1467.

Song J. L., Ellingwood B. R., 1999. Probabilistic modeling of steel moment frames with welded connections. Engineering Journal (AISC), 36(3): 129—137.

Seismic Performance Evaluation of RC Frames withDifferent Seismic Precautionary IntensityBased on Vulnerability Analysis

Xu Chao and Wen Zengping

（Institute of Geophysics, China Earthquake Administration, Beijing 100081, China）

Five RC frames of three-span and six-story were designed with seismic precautionary intensities of Ⅶ、Ⅷ and Ⅸ degree. Vulnerability analysis of the five frames was performed by means of nonlinear dynamic time history analysis. Vulnerability curves based on peak ground acceleration were developed. Seismic performance of the five RC frames was quantitatively evaluated at the point of vulnerability. The effect of fortification criterion on vulnerability was discussed. It shows that, when meeting peak ground acceleration corresponding to small, moderate and large earthquake levels, the failure probabilities of “Undamaged under small earthquake”, “Repairable under moderate earthquake” and “No-collapsing under large earthquake” are less than 18%, which satisfies the three level seismic performance targets. With the increase of seismic precautionary intensity, the exceedance probability of each damage state corresponding to a given peak ground acceleration is reduced. In addition, with increasing one degree of the seismic precautionary intensity, the failure probability of “No-collapsing under large earthquake” decreases. With reducing one degree of the seismic precautionary intensity, the failure probability of “No-collapsing under large earthquake” increases significantly, even up to four times.

Seismic vulnerability; Seismic performance; Nonlinear dynamic time history analysis; Seismic precautionary criterion; RC frame building

10.11899/zzfy20170413

國家科技支撐計劃（2015BAK18B01）；國家自然科學基金（51408561）；中國地震局地球物理研究所基本科研業務費專項（DQJB15C05、DQJB17C04）

2017-04-12

徐超，男，生于1983年。助理研究員。主要從事地震工程方面的研究。E-mail：xuchao@cea-igp.ac.cn

徐超，溫增平，2017．不同設防標準RC框架結構基于易損性分析的抗震性能評估．震災防御技術，12（4）：845—857．