基于正交函數系最小二乘擬合的姿態平滑方法

劉宏建，蔡中祥，劉子義

(信息工程大學 地理空間信息學院，鄭州 450052)

【裝備理論與裝備技術】

基于正交函數系最小二乘擬合的姿態平滑方法

劉宏建，蔡中祥，劉子義

(信息工程大學 地理空間信息學院，鄭州 450052)

針對高速測控目標姿態數據平滑過程中的微小抖動及處理滯后現象，提出了基于正交函數系最小二乘擬合的姿態數據實時平滑方法，該方法具有平滑效果好、實時性強，基本消除了姿態數據的“抖動”現象，對飛行特性不太平穩的目標適應性較強，在無人機試驗中得到了良好的應用。

高速測控目標；正交函數系；最小二乘擬合；實時姿態平滑

無人機、直升機、導彈等由地面測控網跟蹤、量測、控制的飛行目標稱為高速測控目標[1]。有別于常規運動目標，高速測控目標的運動速度快，地面測控網測量獲取的目標實時數據幀率高，單個目標幀率可高達20幀/s，這種由地面測控網實時跟蹤、測量獲得的高速目標實時數據稱為高速測控數據[2]。高速測控數據記錄了飛行目標的實時狀態、位置、方位、姿態、速度、加速度等信息，是分析目標各種性能、指標、參數的基本依據[3]。姿態數據是一類重要的實時測控數據，包括偏航角、側滾角和俯仰角，總稱目標姿態角，是目標相對慣性平臺坐標系的轉動角[3]。

由于受地面測控設備對目標跟蹤精度及靈敏度限制，一般在設備上位機中會對高速測控數據進行平滑濾波處理，但數據平滑濾波往往不能完全消除目標姿態抖動與跳變現象，尤其在地面指控顯示系統中進行目標飛行過程監控時，仍需結合GIS動態顯示機制對目標姿態數據進行二次平滑[4]。目標姿態數據實時平滑算法必須滿足：一是正確性，采用測控設備對目標跟蹤的實測數據作為數據源，要求姿態計算結果準確，目標姿態同目標實時軌跡的走向保持一致；二是穩定性，保證目標姿態實時計算結果平穩、連續，不能出現姿態的突然“抖動”現象，即導彈或直升機、無人機在二三維場景飛行過程中，不能突然出現大幅度 “擺頭”或“掉頭”現象；三是實時性，由于受雷達或光電經緯儀等跟蹤設備數據幀率的限制，目標姿態計算及實時平滑處理算法對每幀數據的處理時間必須小于實時數據幀的幀間隔。

1 主流算法及存在問題

目前，基于GIS的高速測控目標姿態數據實時平滑的方法大致可分為兩類，第一類是基于角度差閾值修正目標姿態角的平滑方法[5-7]，其原理是利用上游目標姿態角序列的方差與經驗常數的乘積作為閾值控制當前姿態角的抖動范圍；第二類是加權最小一乘平滑方法[8-10]，即在最小一乘模型基礎上通過引入自變量權系數設置方式，采用遺傳算法提高算法的收斂速度，以克服異常姿態數據所帶來的影響。上述兩類算法對于飛行特性比較平穩(即飛行曲線較平滑，抖動現象不多)的目標適應性較好，但對于飛行特性不太穩定的目標，還存在下述兩個問題：雖然目標姿態“抖動”幅度下降，但目標姿態“抖動”的頻率并沒有降低，還在進行微小的、頻繁的“抖動”；長時間的連續運行過程中，二三維地圖場景中顯示的目標實時軌跡相對于實際彈道或飛行曲線有明顯的滯后現象。

本文在實驗過程中，深入分析了上述兩個問題產生的原因：上述方法為了保持目標飛行姿態的連續性，限定了目標姿態角的全局閾值，保證了前后兩幀實時數據的姿態角度之差不超過全局閾值。但在進行偏航角修正與平滑時，對當前目標偏航角的修正和對下一數據幀目標偏航角的修正是孤立的；如果目標飛行特性不太平穩，則需要進行頻繁的迭代計算，占用大量CPU處理時間，導致地圖刷新速度下降，因此產生了目標實時軌跡相對于實際飛行曲線有明顯的滯后現象。為解決上述問題，提出并實現了基于正交函數系最小二乘擬合的高速測控目標姿態數據實時平滑方法。

2 基于正交函數系的最小二乘擬合

設φj(x)(j=0,1,2,…,n)是區間[a,b]上的函數，點集(x0,x1,x2,…,xm)?[a,b]，權系數ωi>0(i=0,1,2,…,m)，如果

則稱φj(x)(j=0,1,2,…,n)是關于點集(x0,x1,x2,…,xm)的帶權正交函數系。

若基函數φj(x)(j=0,1,2,…,n)關于點集(x0,x1,x2,…,xm)正交，則最小二乘法方程組的矩陣形式可簡化為

從而解得：

因此，可得最小二乘擬合多項式：

用Gram-Schmidt正交化方法求φj(x)：

這里：

由于平滑算法的強實時性要求，一般采用低階(一階和二階)擬合多項式：

φ0(x)=1

φ2(x)=(x-α2)φ1(x)-β1φ0(x)

φ*(x)=a0*φ0(x)+a1*φ1(x)

φ*(x)=a0*φ0(x)+a1*φ1(x)+a2*φ2(x)

3 算法實現與分析

3.1 算法實現

基于正交函數系最小二乘擬合的高速測控目標姿態平滑算法(以偏航角平滑為例)的實現流程如圖1所示。

圖1 算法實現程序流程

步驟1選取高速目標實時數據幀緩存中的m個數據點形成實測點集數據，點集個數m可作為全局配置參數進行調整，即以m個數據點{P0,P1,P2,…,Pm}作為曲線擬合的數據源；

步驟2在高速目標數據幀緩存中第一次獲取m個實測點值后，對m個數據點進行Gram-Schmidt正交最小二乘擬合，求出擬合方程f(x)；

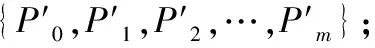
步驟5利用飛行目標當前位置坐標及當前偏航角φm驅動符號(或三維模型)在二三維場景中顯示；

步驟6將本次計算的m個數據點的修正值中的前m-1個點以及實時獲取的下一幀目標數據作為點集數據，轉步驟2進行循環處理。

3.2 應用分析

以某次某型號無人機飛行實時監控應用為例，本文對上述基于正交函數系最小二乘擬合的姿態實時平滑方法進行了驗證，分別選取點集個數m=6，m=9，m=12時，處理延時如表1所示。

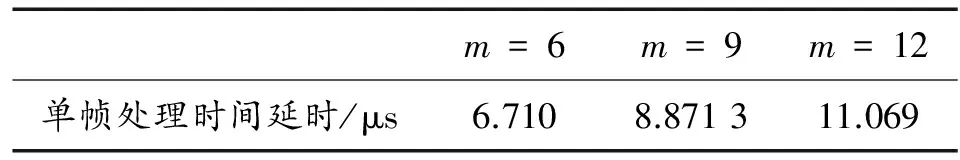
表1 m取值與單幀處理延時關系

可見，算法可以很好地對飛行目標姿態進行平滑處理，使目標能夠在二三維場景連續、平穩的運動，無“抖動”現象，并且m值越大，飛行目標姿態平滑的效果越好。當m=6時，單幀目標實時數據處理延時為6.710 μs，當m=12時，單幀目標實時數據處理延時為11.069 μs，從單幀數據處理延時來看，算法的實時性較強，遠小于50 ms(跟蹤測控設備的數據幀率)的限制。取m=6，無人機姿態平滑前后對比如圖2所示。

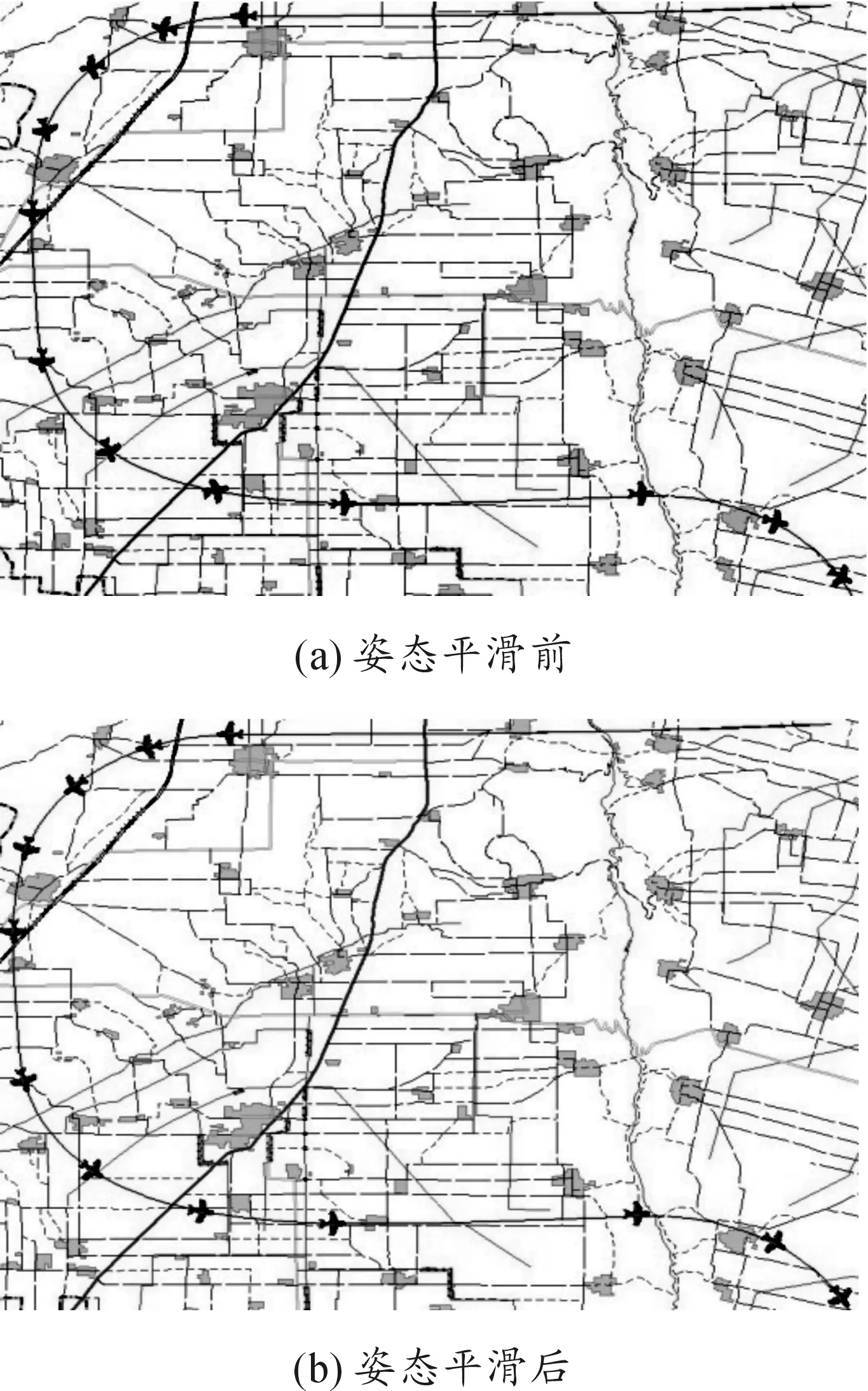
圖2 無人機姿態平滑前后對比

4 結論

本文分析了現有高速測控目標姿態數據實時平滑算法存在的主要問題，提出并實現了基于正交函數系最小二乘擬合的高速測控目標姿態平滑方法。該方法基本消除了姿態數據的“抖動”現象，對飛行特性不太平穩的目標適應性較強，在實際應用中取得了良好的效果。

[1] 常顯奇，程永生.常規武器裝備試驗學[M].北京：國防工業出版社，2007.

[2] 劉宏建，劉建忠，蔡中祥.應用“緩存分流”模型的高速測控目標全軌跡顯示算法研究[J].測繪科學，2013,38(5):94-96.

[3] 何友金.靶場測控概論[M].濟南:山東大學出版社，2009.

[4] 王麗娜.基于GIS的飛行器定位中的匹配方法[J].空間控制技術與應用，2011,37(1):33-35.

[5] 吳文江，陳其工，高文根.基于 PSO 優化參數的最小二乘支持向量機短期負荷預測[J].重慶理工大學學報(自然科學)，2016(3)：112 - 115.

[6] 劉宏建.常規武器裝備靶場試驗地理空間分析與應用建模研究[D].鄭州：信息工程大學，2008.

[7] 王東霞，石恒，賈英宏.航天器姿態指向跟蹤的一種自適應滑模控制方法[J].空間控制技術與應用，2010,36(6):22-26.

[8] KOENIG S,LIKHACHEV M.Improved Fast Replanning for Robot Navigation in Unknown Terrain[C]//Proceeding of the 2012 IEEE international Conference on Robotics & Automation,Washington,DC,USA.USA:IEEE,2012:968-975.

[9] 徐小輝，郭小紅.外彈道加權最小一乘模型研究與應用[J].飛行器測控學報，2008,27(2):85-88.

[10]FERGUSON D,STENTZ A.The Field D*Algorithm for Improv Fed Path Planning and Replanning in Uniform and Non-uniform Cost Environments [R].Technical Report CMU-RI-TR-05-19.USA:Carnegie Melton School of Computer Science,2005.

(責任編輯周江川)

Attitude Smoothing Method Based on Least Square Fitting of Orthogonal Function System

LIU Hong-jian, CAI Zhong-xiang, LIU Zi-yi

(Institute of Geospatial Information, PLA Information Engineering University, Zhengzhou 450052, China)

Aiming at the small jitter and delay processing phenomenon in high speed measurement and control target attitude data smoothing, we put forward a real-time attitude data smoothing method based on least square fitting of orthogonal function system. The method has good effect and real-time performance, basically eliminates the “chattering” phenomenon of attitude data, and gets a good application in UAV test.

high-speed measurement and control target; orthogonal function system; least squares; real time attitude data smoothing

2016-08-15；

2016-09-20

國家自然科學基金項目(41301125)

劉宏建(1980—)，男，博士，講師，主要從事軍事地理學與作戰環境分析方法研究。

10.11809/scbgxb2017.01.005

劉宏建，蔡中祥，劉子義.基于正交函數系最小二乘擬合的姿態平滑方法[J].兵器裝備工程學報，2017(1):21-23.

format:LIU Hong-jian, CAI Zhong-xiang, LIU Zi-yi.Attitude Smoothing Method Based on Least Square Fitting of Orthogonal Function System[J].Journal of Ordnance Equipment Engineering,2017(1):21-23.

P231

A