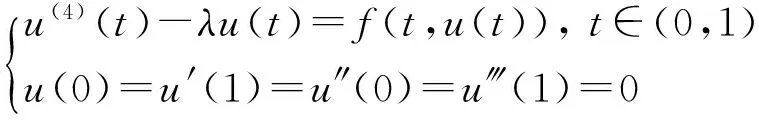一類四階微分方程兩點邊值問題正解及多個正解的存在性
李 洋
(南京航空航天大學 理學院, 南京 211100)
一類四階微分方程兩點邊值問題正解及多個正解的存在性
李 洋
(南京航空航天大學 理學院, 南京 211100)
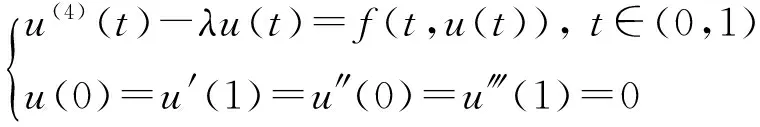
四階邊值問題;不動點指數;正解;第一特征值
微分方程邊值問題是當今國內外熱門研究課題之一,尤其是微分方程邊值問題正解的存在性更受青睞。梁是工程建筑的重要構件之一,根據梁的兩端支撐條件不同,會得到不同的四階邊值問題。由于其在工程上的重要性,近年來有較多文獻研究了其正解的存在性[1-8]。然而對于描述一端簡單支撐、另一端滑動支撐的彈性梁平衡態的四階微分方程研究則比較少。
文獻[9]研究了如下的四階邊值問題正解的存在性:
(1)
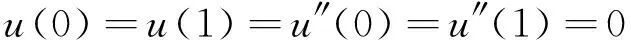
(2)
其中f(t,u)∈C([0,1]×[0,∞),[0,∞))。利用不動點指數理論考慮四階邊值問題當參數λ在[0,∞)變化時正解的存在性。
受以上文獻的啟發,本文研究一類四階微分方程正解及多個正解的存在性,方程如下:
(3)
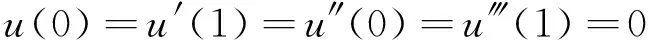
(4)
1 預備知識與引理
本文總假定:(H1)f∈C([0,1]×[0,∞),[0,∞))。
為敘述方便,引入下列記號
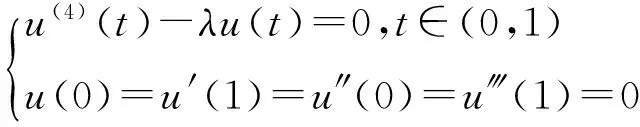
引理1 邊值問題-u″(t)=0,t∈(0,1),u(0)=u′(1)=0的格林函數為
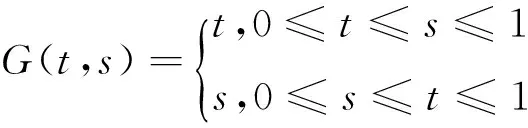
且G(t,s)有以下性質:
1)G(t,s)≥0,G(t,s)≤G(s,s);
2)G(t,s)≥G(t,t)G(s,s)。
記
定義算子A:C+[0,1]→C+[0,1],有
(5)
記
顯然,K是C[0,1]中的一個錐。
引理2A(K)?K且A全連續。
證明 對于u?K,由式(5)及引理1知,Au(t)≥0,t∈[0,1],且
(6)
因此
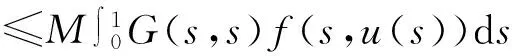
另一方面由引理1得
(7)
由式(6)和(7)可得
(8)
因此A(K)?K。另外由f的連續性及Arzela-Ascoli定理可證A是全連續的。
對r>0,記Kr={u∈K∶‖u‖ 引理3[10]設A:K→K是全連續的,并且對任意u∈?Kr和0<μ≤1,有μAu≠u,則i(A,Kr,K)=1。 引理4[10]設A:K→K是全連續的,并假設以下2個條件滿足: 2) 對任意的u∈?Kr和μ>1,有μAu≠u,則i(A,Kr,K)=0。 證明 由f0 (9) 設r∈(0,r0],下證μAu≠u,u∈?Kr,0<μ≤1。事實上,若存在u0∈?Kr,0≤μ≤1,有μ0Au0=u0,顯然u0滿足 (10) (11) 由式(8)知 (12) 因此 故L≤(L-ε),矛盾。由引理3知 (13) 又由f∞>L知,存在ε∈(0,L)及H>r0,使得 (14) 設 則 (15) 下證μAu≠u,u∈?KR,μ≥1。事實上,若存在u0∈?KR,μ0≥1,使μ0Au0=u0,顯然u0滿足式(10)和邊值條件(4),結合式(15),類似式(11)的證明,有 因此 再結合式(12)得 (16) 證明 由f0>L可知,存在ε∈(0,L)及r0>0,使得 (17) 設r∈(0,r0],對任意的u∈?Kr,結合式(17)得 下證μAu≠u,u∈?KR,μ≥1。事實上,若存在u0∈?KR,μ0≥1,使μ0Au0=u0。顯然u0滿足式(10)和邊值條件(4),結合式(17),類似式(11)的證明,有 仍可得出矛盾。由引理4知 (18) 又由f∞ 設 則 (19) 如果存在u0∈?Kr,0≤μ≤1,有μ0Au0=u0,則結合式(19)得 因此 結合式(12)得 則當R>R0時,u∈?KR,0<μ≤1,,都有μAu≠u成立。因此,由引理3得 (20) 下面證明對任何u0∈?Kp,μ0≥1,使μ0Au0=u0,則對于t∈[0,1],有0≤u≤p,故由條件(H2)類似于式(11)證明可得 這顯然與a>L矛盾,由此由引理4可得 (21) 由f0 (22) 又由f∞ (23) 取R>p>r,由式(21)~(23)得 又因f滿足條件(H1)和(H2),則存在t0∈[0,1],使得f(t0,u0(t))>0,故有 [1] MA R,WANG H.On the existence of positive solutions of fourth-order ordinary differential equations[J].Appl Anal,1995,59:225-231. [2] LI Y.Positive solutions of fourth-order boundary-value problem with two parameters[J].J Math Anal Appl,2003,281:477-484. [3] GUO D,LAKSHMIKANTHAM V.Nonlinear Problems in Abstract Cones[M].New York:Academic press,1988. [4] 李永祥.一類四階邊值問題正解的存在性[J].純粹數學與應用數學,2000,16(3):54-58. LI Yongxiang.The existence of Positive solution sofa fourth-order boundary value problem[J].Pure and Applied Mathematics,2000.16(3):54-58. [5] 柴國慶,黃朝炎.變系數四階邊值問題正解的存在性[J].數學物理學報,2007,27A(6):1065-1073. CHAI Gouqing,HUANG Chaoyan.Existence of Positive Solutions for Furth-Order Boundary Value Problem with Variable Coefficients[J].Acta Mathematica Scientia,2007,27A(6):1065-1073. [6] 楊變霞,路艷瓊,陳瑞鵬.一類四階兩點邊值問題正解的存在性[J].純粹數學與應用數學,2011,27(2):273-279. YANG Bianxia,LU Yanqiong,CHEN Ruipeng.Existence of positive solutions for a fourth-order two-point boundary value problem[J].Pure and Applied Mathematics,2011,27(2):273-279. [7] 盧整智,韓曉玲.一類四階兩點邊值問題多個正解的存在性[J].西南大學學報(自然科學版),2013,35(4):79-83. LU Zhengzhi,HAN Xiaoling.Existence of Multiple Positive Solutions of a Class of Fourth-order Two-Point Boundary Value Problem[J].Journal of Southwest University(Natural Science Edition),2013,35(4):79-83. [8] 張銳, 盧整智.一類彈性梁方程多個正解的存在性[J].杭州師范大學學報(自然科學版),2015,14(5):522-526. ZHANG Rui,LU Zhengzhi.A Hardy-Hilbert Type Inequality with Multi-Parameters and its Applications[J].Journal of Hangzhou Normal University(Natural Science Edition),2015,14 ( 5):522-526. [9] CHEN T L.Existence of positive solutions for a class of fourth-order ordinary differential equations of two-point boundary value problem[J].Chinese journal of engineering mathematics,2010,27(4):679-683. [10]郭大鈞.非線性泛函分析[M].濟南:山東科學技術出版社,2003. GUO Dajun.Nonlinear Functional Analysis[M].Jinan:Shandong science and technology press,2003. (責任編輯 陳 艷) Existence and Multiplicity of Positive Solutions for a Class of Fourth-order Differential Equations of Two-Point Boundary Value Problem LI Yang (Department of Mathematics, Nanjing University of Aeronautics of Astronautics,Nanjing 21100, China) fourth-order boundary value problem;fixed point index; positive solution; first eigenvalue. 2016-04-13 國家自然科學基金資助項目(11572148);高等學校博士學科點專項科研基金資助項目(20133218110025) 李洋(1991—),女,江蘇淮安人,碩士研究生,主要從事非線性分析研究,E-mail: 1146959574@qq.com。 李洋.一類四階微分方程兩點邊值問題正解及多個正解的存在性[J].重慶理工大學學報(自然科學),2017(1):158-164. format:LI Yang.Existence and Multiplicity of Positive Solutions for a Class of Fourth-order Differential Equations of Two-Point Boundary Value Problem[J].Journal of Chongqing University of Technology(Natural Science),2017(1):158-164. 10.3969/j.issn.1674-8425(z).2017.01.024 O175 A 1674-8425(2017)01-0158-07
2 主要結果