拓撲優化與尺寸優化相結合的割草車車架輕量化設計

陳遠帆，李舜酩，蘇玉青

(南京航空航天大學 能源與動力學院，南京 210016)

拓撲優化與尺寸優化相結合的割草車車架輕量化設計

陳遠帆，李舜酩，蘇玉青

(南京航空航天大學 能源與動力學院，南京 210016)

車架輕量化是節能和降低成本的重要途徑。針對某型號割草車車架，提出了將拓撲優化與尺寸優化相結合的割草車車架輕量化設計方法。在滿足工作性能和車架強度的基礎上，利用有限元仿真技術，分別對割草車車架進行了彎曲工況與扭轉工況下的強度分析，以分析結果為基礎，進行拓撲優化與尺寸優化相結合的二級優化，并對優化前后車架的強度進行對比分析。結果表明：最終優化后車架強度滿足要求，且最終優化后車架比未優化前減少質量34.3%，輕量化效果顯著。

割草車車架；有限元分析；拓撲優化；尺寸優化

節能環保始終是世界發展的主題，從全球范圍來看，能源總量是有限的，隨著經濟的快速發展，能源消耗也不斷增加。研究數據表明：汽車每減重10%，油耗可以降低6%～8%[1]。進行輕量化研究可以減少能源消耗，降低制造和使用成本，提高經濟效益，所以輕量化研究有重要意義[2-4]。國內外已有較多學者對輕量化設計進行了研究。文獻[5]對摩托車車架進行了優化設計，使其質量減小，輕量化效果顯著。文獻[6-8]對以鋼鐵為原料的結構零部件進行了優化，有效降低了質量。文獻[9-10]對車架采用尺寸參數優化的方法進行輕量化設計，輕量化效果明顯。尺寸優化通常是對單元尺寸進行優化[11-12]，較易達到優化目標，但很難對原有結構進行較大改進；拓撲優化[13]則可以通過約束載荷條件尋求最優的拓撲結構，該方法較之于尺寸優化難度更大，但是該方法的特點是可以改變原有結構形式。割草車車架作為整車各主要零部件的安裝基體，承受著自身的重力以及各部件與車架之間的作用力。車架的可靠性直接影響整車的運行以及駕駛員的安全，因此，輕量化設計要在滿足強度要求的條件下進行。割草車車架既有梁結構又有板結構，在整體結構和單元尺寸上都有改進空間。因此，本文結合拓撲優化與尺寸優化各自的優點，先進行拓撲優化，在拓撲優化基礎上再進行尺寸優化。最終得到所需要的車架結構，并與原有車架進行強度校核對比，檢驗優化結果的優劣，達到比單一優化更好的效果。

1 割草車車架原始模型的建立

割草車由于其功用與傳統乘用車、貨車等的不同，在車架形式上有較大不同。整個車架主要由左右長梁、前后支撐橫梁、后擋板、電池座、前大板等27個部件組成。車架模型采用Solidworks軟件進行建立，并簡化不必要的部件，其余部件根據實際尺寸進行建模。各個部件之間根據實際情況施加約束。裝配完成后模型如圖1所示。

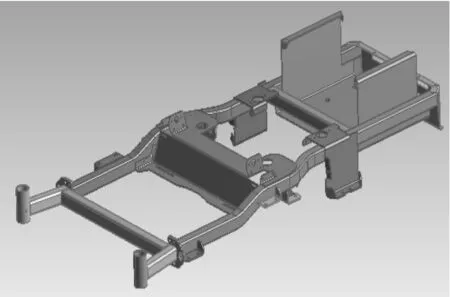
圖1 割草車車架原始模型Fig.1 The original model of the cutting grass car frame

2 車架強度分析

2.1 強度分析基本理論

鋼、銅、鋁等塑性材料，通常以屈服的形式失效，有限元[14-20]分析中可以通過Von Mises等效應力的大小來判斷材料的靜態強度。該車架的材料是Q235鋼，屈服強度σs=235 MPa，彈性模量E=210 GPa，泊松比ν=0.3。滿足強度要求的條件是最大應力不超過材料的許用應力。等效應力可以表示為

(1)

滿足強度條件應當：σr≤[σ]，其中：σr表示相當應力；σ1，σ2，σ3分別表示第一、第二、第三主應力；[σ]表示材料許用應力，并且σs/[σ]=n，n表示安全系數。

2.2 兩種典型工況強度分析

割草車在工作的過程中，由于載荷的不同，車架會產生不同變形，以彎曲變形和扭轉變形最為常見，對應彎曲工況和扭轉工況這兩種典型工況。這兩種是汽車最基本的，也是對車架影響較大的工況。因此，本文選取彎曲工況和扭轉工況這兩種典型工況來校驗車架強度。

采用ANSYS workbench作為分析軟件，導入Solidworks中建立的模型進行靜力分析。車架的載荷及約束按照實際情況進行施加。車架的主要受力有車架前部刀盤對車架的作用力、車架中部駕駛員對車架的作用力、車架后部電池包對車架的作用力、車架自身質量。其中，駕駛員質量為90 kg，刀盤質量為98 kg，電池包質量為80 kg。

2.2.1 彎曲工況

彎曲工況約束施加成整個車架四個支承處的固定約束。車架各部分之間約束均為綁定。具體載荷及約束施加如圖2所示。經過計算可以得到應力結果，其中Von Miss等效應力云圖如圖3所示。

圖2 彎曲工況載荷及約束施加Fig.2 The load and the constraints on the bending condition

圖3 彎曲工況Von Mises等效應力云圖Fig.3 The Von Mises equivalent stress nephogram on the bending condition

由圖3可以看出：整體車架最大等效應力為39.5 MPa，其余區域應力基本不超20 MPa。本文選取安全系數為3，可得許用應力[σ]=78.3 MPa，所以最大等效應力σr≤[σ]。在彎曲工況下，選取較大的安全系數，車架強度滿足要求，且仍然有很大余量，有較大優化空間。

2.2.2 扭轉工況

扭轉工況釋放一個前端支承垂直方向的自由度，其余3個支承固定約束。車架各部分之間約束均為綁定。具體載荷及約束施加如圖4所示。經過計算可以得到應力結果，其中Von Miss等效應力云圖如圖5所示。

圖4 扭轉工況載荷及約束施加Fig.4 The load and the constraints on the torsion condition

圖5 扭轉工況Von Mises等效應力云圖Fig.5 The Von Mises equivalent stress nephogram on the torsion condition

從圖5可以看出：整體車架最大等效應力53.1 MPa，其余部分應力基本不超20 MPa。本文選取安全系數為3，可得許用應力[σ]=78.3 MPa，最大等效應力σr≤[σ]，所以在扭轉工況下，選取較大的安全系數，車架強度滿足要求，且仍然有很大余量，有較大優化空間。

3 車架優化設計

由兩種典型工況的分析可以看出，車架整體應力較小，車架強度有很大余量，在材料的利用上有很大的浪費。所以有必要進行輕量化設計。拓撲優化和尺寸優化的對象特點不同，一般用于不同場合。割草車車架既有梁結構又有板結構，在整體結構和單元尺寸上都有改進空間。因此，本文采用拓撲優化及尺寸優化兩級優化方法來進行優化設計，以期達到較好的減少質量的目的。

3.1 優化設計基本概念及輕量化設計方案

3.1.1 拓撲優化基本概念

拓撲優化設計的目的是在指定的設計空間內尋求形狀和材料的最佳分布，一般用于概念設計階段。結構拓撲優化的基本設計思想是把尋找結構的最優拓撲結構問題轉化為在給定的設計區域內尋找最優材料分布的問題。在產品的概念設計階段，僅僅通過經驗來設計結構是不夠的，只有進行拓撲優化設計分析，并結合設計人員豐富的設計經驗，才能在前期的概念設計階段中得出合理的方案，最終得到滿足各項要求的設計產品。連續體拓撲優化的本質是0-1離散變量的組合問題，常用方法是變密度法。

拓撲優化過程中選取單元密度為設計變量，數學模型可以寫成：

最小化：

(2)

約束條件：

(3)

其中：X=x1,x2,…,xn是設計變量；f(x)是目標函數；g(X)是不等式約束函數；h(X)是等式約束函數；xi表示設計變量，L表示下限，U表示上限。

3.1.2 尺寸優化基本概念

尺寸優化設計是在不改變目標拓撲結構、幾何外形和材料屬性的前提下，以尺寸參數為設計變量，通過具體的數學模型優化算法來優化該參數，使結構的質量或體積達到最小。尺寸優化設計用于詳細設計階段，通過改變結構單元的屬性(如殼單元的厚度，桿的橫截面積等)，來滿足一定的設計要求(如應力、頻率、位移等)。所以使用有限元的方法計算結構位移和應力時，不會改變目標的拓撲結構等尺寸參數以外的屬性，可以直接對現有的結構尺寸參數進行優化設計，最大程度地降低成本，提高結構性能。

在尺寸優化過程中，選取各部件厚度為設計變量，數學模型可以表示為：

最小化：

(4)

約束條件：

(5)

其中：M為車架結構總質量；ρ為材料密度；vi為單元體積；n為單元的個數；σmax為有限元分析中單元節點的最大應力值；σe為材料屈服極限；xi表示設計變量，L表示下限，U表示上限。

車架輕量化設計方案流程如圖6所示。

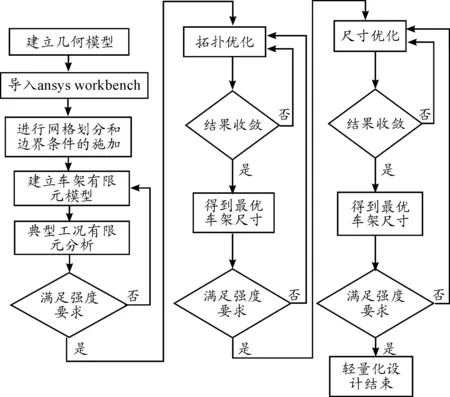
圖6 車架輕量化設計方案流程Fig.6 The lightweight design process of the frame

3.2 拓撲優化

分別選取彎曲工況和扭轉工況進行拓撲優化，兩種工況優化步驟基本相同。具體步驟如下：

1) 在兩種工況下進行車架的靜力分析。將車架模型導入workbench，在靜力分析模塊中設定材料屬性及載荷和約束，分網完成后進行靜力求解。

2) 在完成靜力分析以后，在靜力分析模塊后插入shape optimization模塊。進入該模塊進行載荷和約束的施加，所施加的載荷與約束和靜力分析相同，并在target reduction中設定減重30%。設定完以后進行拓撲優化的求解。

3) 根據拓撲優化結果進行模型的修改，并將修改后的模型再進行靜力分析，檢驗修改后的結果是否滿足要求。

整體拓撲優化結果如圖7所示。在圖7中，紅色區域為理論上可以去除的部分，但是實際修改模型時，一般會根據實際情況進行相對規則的去除。理論上，紅色區域可以完全去除，但是實際上有些紅色區域可能是與某些已經簡化掉的部件相關聯，所以有時并不能完全去除。

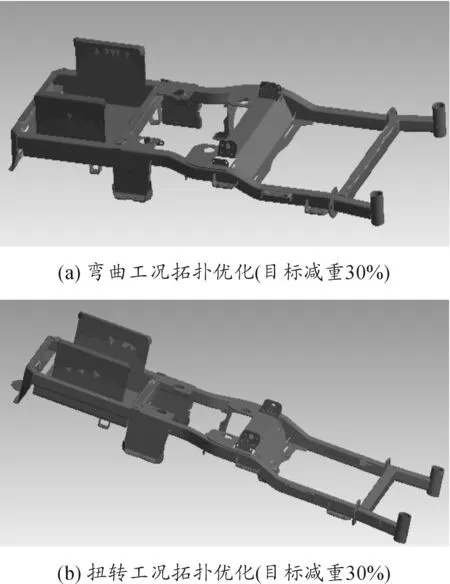
圖7 整體拓撲優化結果Fig.7 The results of overall topology optimization

在整個車架中，主要零部件有左右長梁、前后橫梁、電池座、后擋板和前大板。因此，拓撲優化主要目標選為這幾個部件，根據圖7進行這幾個零部件的拓撲修改。將電池座左右擋板切除至與左右長梁等高；將后擋板的上下邊緣進行挖孔操作；后橫梁前面進行挖孔操作；前橫梁前面與后面都進行挖孔操作；左右長梁后端進行挖孔操作；前大板不進行拓撲修改。修改后各零部件圖形如圖8所示。

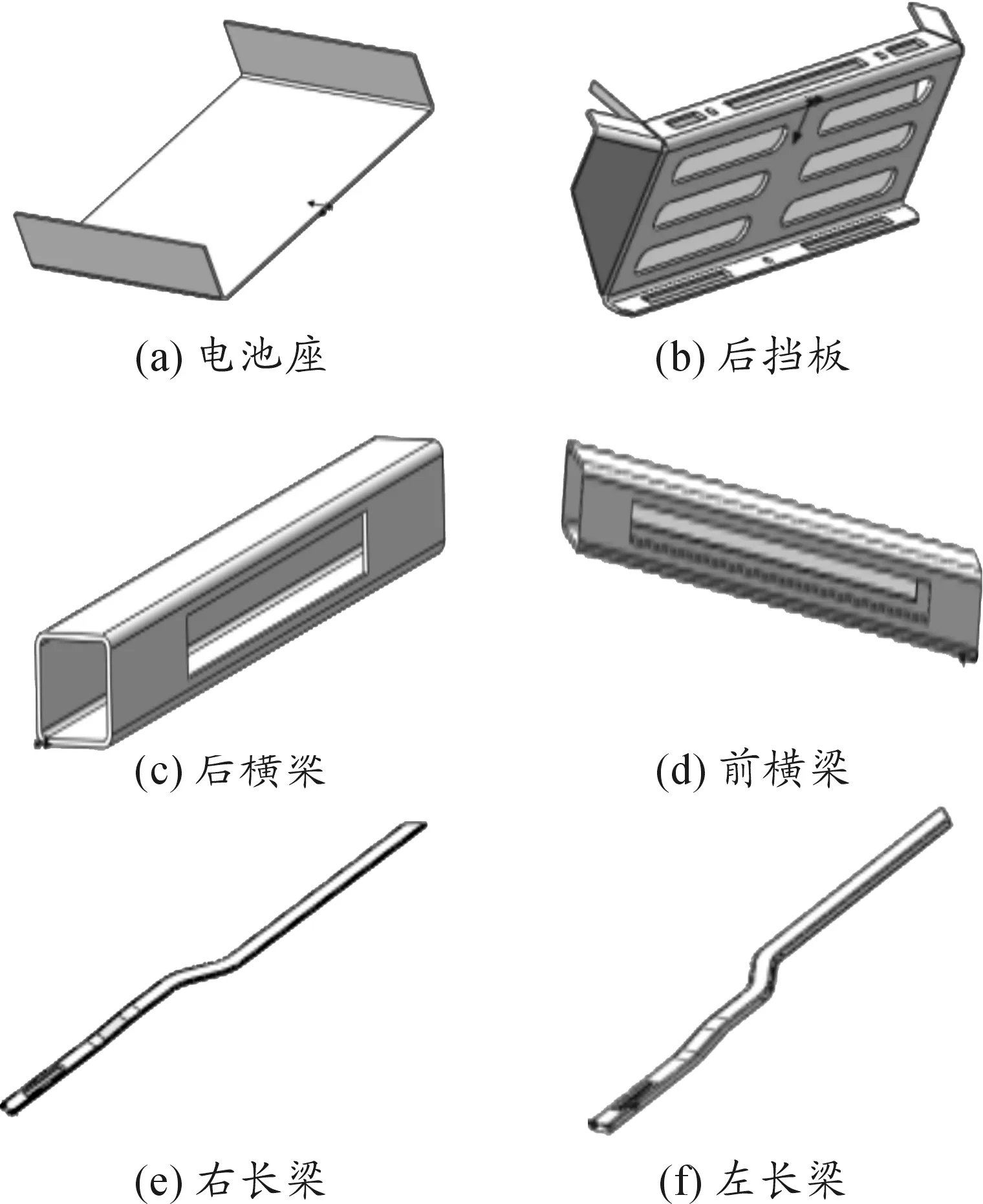
圖8 主要部件拓撲修改結果Fig.8 The topological modification results of the main components

根據修改結果，重新進行彎曲與扭轉工況強度校核，計算結果如圖9所示。

由圖9可以發現：修改后兩種工況最大應力分別為43 MPa和44 MPa，其余部分應力基本不超20 MPa。本文選取安全系數為3，可得許用應力[σ]=78.3 MPa，所以最大等效應力σr≤[σ]，滿足強度要求。整體車架原質量為67.075 kg，通過拓撲優化，整體車架質量減少至59.69 kg，減輕了7.385 kg，減輕了11%，取得較好的效果。但整體車架大部分區域應力仍然較小，還有進一步優化的空間。

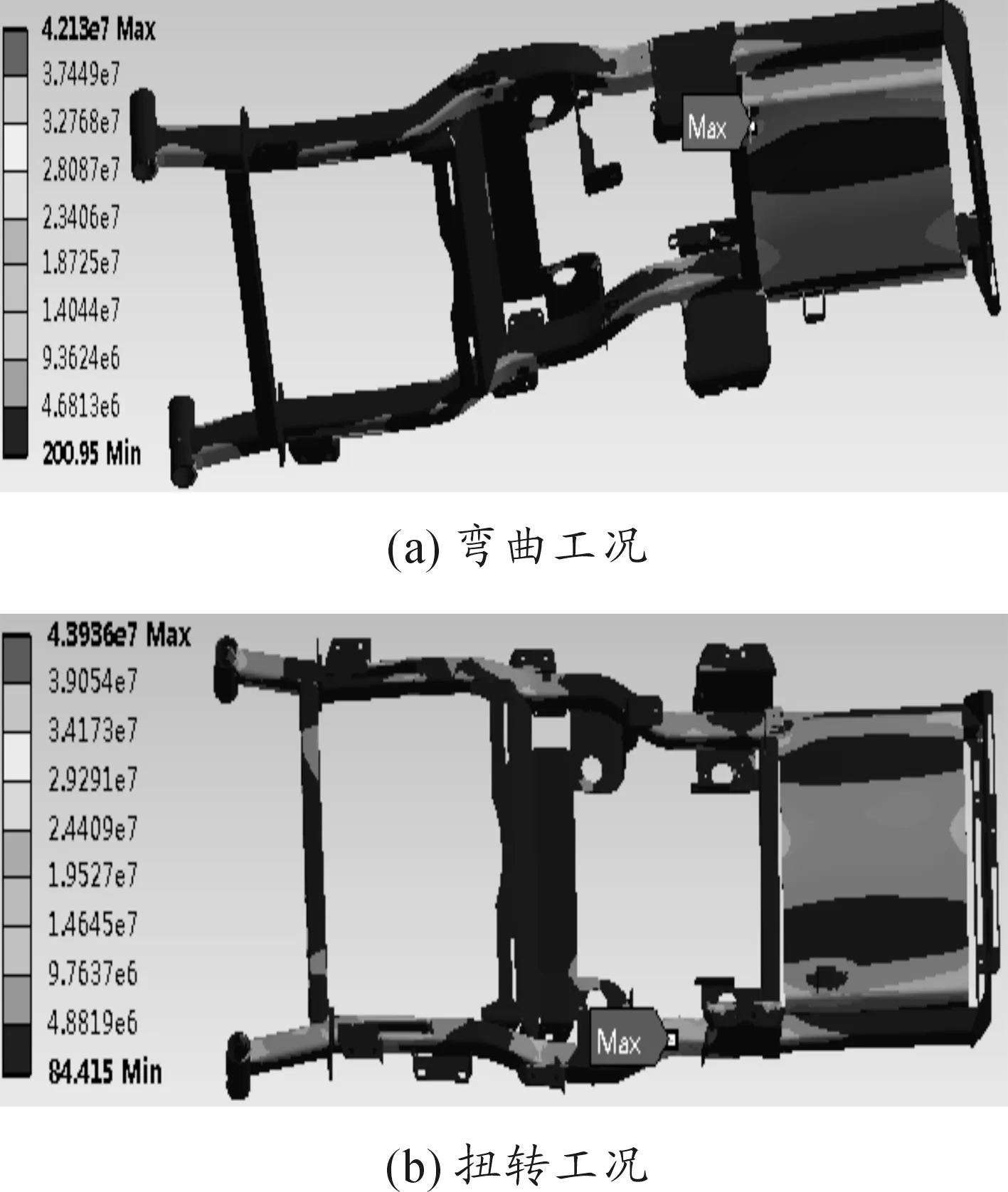
圖9 Von Mises等效應力云圖Fig.9 The Von Mises equivalent stress nephogram

3.3 尺寸優化

在拓撲優化的基礎上，選取大板厚度、電池座厚度、左右長梁的厚度、前橫梁厚度、后橫梁厚度、以及后擋板厚度這7個尺寸參數作為設計變量，約束條件設定為最大等效應力不超過許用應力，目標函數設定為質量最小。采用ANSYS workbench分別對彎曲工況以及扭轉工況進行目標驅動優化。

ANSYS workbench采用Design Explorer作為其優化工具，該工具是通過設計點的參數來研究輸出參數的。但是一般輸入設計點是有限的，所以，通常是通過有限個設計點擬合成響應曲面來研究的。根據選取的7個尺寸參數，軟件會生成79個設計點。通過計算，再根據設定的約束條件以及目標函數，在兩種工況下，各會生成一個推薦的最優設計點，將這兩個設計點插入原始有限元模型進行靜力計算。尺寸數值的選取和計算結果如表1所示。

表1 目標驅動優化結果Table 1 The results of the goal-driven optimization

根據兩種工況的計算結果，選取能使兩種工況強度均滿足要求的尺寸數值，最終選取結果如表2所示。接下來進行強度校核，計算可得在兩種工況下等效應力如圖10所示。

表2 尺寸優化修改結果Table 2 The results of the size optimization modification

由圖10可以看出，彎曲工況下，最終修改模型的Von Mises等效應力最大為60.37 MPa，在安全系數取3的情況下，小于許用應力[σ]=78.3 MPa，滿足強度要求；在扭轉工況下，最終修改模型的Von Mises等效應力最大為72.34 MPa，在安全系數取3的情況下，小于許用應力[σ]=78.3 MPa，因此也滿足強度要求。經過拓撲優化和尺寸優化兩級優化后車架質量減為44.053 kg，原始質量為67.075 kg，下降了23.022 kg，下降了34.3%，取得了很好的輕量化效果。優化后車架質量及質量減少百分比如表3所示。

圖10 Von Mises等效應力云圖Fig.10 The Von Mises equivalent stress nephogram表3 優化后車架質量及質量減少百分比Table 3 The weight loss percentage and quality of the optimized frame

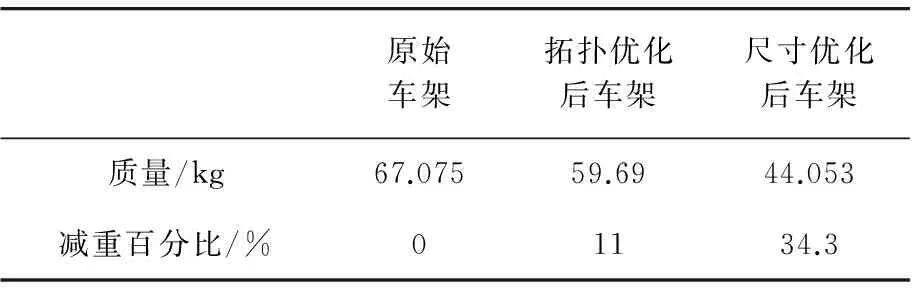
原始車架拓撲優化后車架尺寸優化后車架質量/kg67.07559.6944.053減重百分比/%01134.3

4 結論

1) 本文通過Solidworks軟件進行了割草車車架的參數化建模，并運用ANSYS workbench進行彎曲工況與扭轉工況下的強度分析。兩種工況最大等效應力分別為39.5 MPa和53.1 MPa，大部分區域應力不超20 MPa，小于許用應力78.3 MPa，滿足強度要求，整體車架有很大優化空間。

2) 進行了拓撲優化，優化后車架兩種工況下最大應力分別為43 MPa和44 MPa，小于許用應力78.3 MPa，滿足強度要求，且仍有進一步優化的空間。整體車架質量從67.075 kg減少至59.69 kg，減輕了7.385 kg，減輕了11%，初步取得較好的效果。

3) 進一步進行了尺寸優化，優化后車架兩種工況下最大應力分別為60.37 MPa和72.34 MPa，小于許用應力78.3 MPa，滿足強度要求。整體車架質量從59.69 kg減少至44.053 kg，又減輕了15.637 kg，通過兩級優化共減輕了23.022 kg，最終減輕了34.3%，輕量化設計效果顯著。

[1] BENEDYK J.Light metals in automotive applications[J].Light Metal Age-Chicago,2000,58(9/10):34-35.

[2] 趙韓,錢德猛.基于 ANSYS 的汽車結構輕量化設計[J].農業機械學報,2005,36(6):12-15.

ZHAO Han,QIAN Demeng.Research on Lightweight Design of Automobile Structure Based on ANSYS[J].Journal of agricultural machinery,2005,36 (6):12-15.

[3] 成耀龍,馬力,王皎.重型專用車車架輕量化結構優化設計[J].專用汽車,2006(2):29-32.

CHENG Yaolong,MA Li,WANG Jiao.Structure optimum design based lightweight on special heavy vehicle frame[J].Journal of special vehicles,2006 (2):29-32.

[4] 鐘佩思,孫雪顏,趙丹,等.基于 ANSYS 的貨車車架的有限元靜態分析[J].拖拉機與農用運輸車,2008,35(2):89-93.

ZHONG Peisi,SUN Xueyan,ZHAO Dan,et al.FEM static analysis of truck frame model based on ANSYS[J].Journal of tractors and agricultural transport vehicles,2008,35 (2):89-93.

[5] MATSUMOTO，MASAHIDE，ABE．Structural optimization for configuration design of the motorcycle body[C]//Proceedings of the 6th International pacific conference on automotive engineering，1991，10：1399-1406．

[6] Ultra light steel auto body final report[Z]．Porsche Engineering Services.1998.

[7] Ultra light steel auto body final report[Z]．Porsche Engineering Services，Inc．2001.

[8] Ultra light steel auto body final report[Z]．Lotus Engineering Services，Inc．2001．

[9] 馬迅,過學迅,趙幼平,等.基于有限元法的結構優化與靈敏度分析[J].機械科學與技術,2002,21(4):558-561.

MA Xun,GUO Xuexun,ZHAO Youping,et al.Structural optimization and sensitivity analysis based on finite element method[J].Journal of mechanical science and technology,2002,7:558-561.

[10]宋發寶.大型天線座車車架輕量化設計研究[D]．武漢：武漢理工大學，2008．

SONG Fabao.Structural lightweight research on frame of large rader antenn vehicle[D].Wuhan:Wuhan university of science and technology,2008.

[11]張國鋒,王衛榮.基于 ANSYS Workbench 的吊座尺寸多目標優化設計[J].機械工程與自動化,2014,1:69-73.

ZHANG Guofeng,WANG Weirong.Multi-objective optimization design of the size of tower crane based on ANSYS Workbench[J].Journal of mechanical engineering and automation,2014,1:69-73.

[12]姚道壯,楊建國,呂志軍.基于 ANSYS Workbench 的貨架立柱截面優化設計[J].東華大學學報:自然科學版,2011,37(4):438-441,475.

YAO Daozhuang,YANG Jianguo,LV Zhijun.Optimization of steel storage rack column cross-sections based on ANSYS workbench[J].Journal of donghua uversity:natural science edition,2011,37 (4):438-441475.

[13]黃雪濤,王海霞,鐘佩思.礦用三輪汽車車架拓撲優化設計[J].煤礦機械,2016,37(5):116-117.

HUANG Xuetao,WANG Haixia,ZHONG Peisi.Topology optimization design of mine three-wheels vehicle frame[J].Journal of coal mine machinery,2016,37 (5):116-117.

[14]尤曉鎮,隆志力,傅惠,等.基于有限元模型的超聲切割刀優化設計[J].壓電與聲光,2015,37(6):1083-1087.

YOU Xiaozheng,LONG Zhili,FU Hui,et al.Optimization Design of Ultrasonic Knife Cutting System Based on Finite Element Model[J].Piezoelectrics & Acoustooptics,2015,37(6):1083-1087.

[15]江旭東.冠脈支架對彎曲血管損傷機理的非線性有限元分析[J].功能材料,2015(3):3050-3054.

JIANG Xudong.The nonlinear finite element analysis of curved vascular[J].Journal of Functional Materials,2015(3):3050-3054.

[16]宛汀,時艷玲.微波無源器件的快速有限元全波分析[J].電子元件與材料,2015(8):78-82.

WAN Ting,SHI Yanling.Fast finite-element full-wave analysis for the microwave[J].Electronic Components & Materials,2015(8):78-82.

[17]四庫.激光透射焊接聚碳酸酯的有限元數值模擬[J].激光雜志,2015(6):104-107.

SI Ku.Finite element analysis of laser transmission welding of polycarbonate[J].Laser Journal,2015(6):104-107.

[18]劉祥沛,董天文,鄭穎人.有限元荷載增量法在判定樁基礎極限荷載的應用[J].四川兵工學報,2016,37(5):144-148.

LIU Xiangpei，DONG Tianwen，ZHENG Yingren．Application of Incremental Load Method of FEM in Determining the Ultimate Load of Pile Foundation[J].Journal of Ordnance Equipment Engineering，2016(5):144-148．

[19]劉昌奇,徐余法,李全峰,等.基于有限元分析的一種超超高效異步電機[J].電機與控制應用,2015(5):75-80.

LIU Changqi,XU Yufa,LI Quanfeng,et al.A ultra-super efficiency asynchronous motor based on the finite element analysis[J].Electric Machines & Control Application,2015(5):75-80.

[20]李杏芮,陳清,盛華均,等.膝關節三維有限元模型的構建及生物力學分析[J].西南大學學報(自然科學版),2015,37(5).

LI Xingrui,CHEN Qing,SHENG Huajun,et al.Construction and biomechanics analysis of three-dimensional finite element model for The knee joint[J].Journal of Southwest University(Natural Science Edition),2015,37(5).

(責任編輯 楊文青)

The Light-weight Design of the Cutting Grass Car Frame Combined the Topology Optimization with the Size Optimization

CHENG Yuan-fan, LI Shun-ming, SU Yu-qing

(College of Energy and Power Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)

The frame lightweight is an important way of energy saving and cost reduction. This paper based on a frame of a cutting grass car, puts forward a design method combined the topology optimization with the size optimization for the lightweight of cutting grass car frame. On the premise of meeting the working performance and the strength of frame, this paper uses the finite element simulation technology to go on the strength analysis under the bending condition and torsion condition. On the basis of the analysis results, it continues the secondary optimization combined the topology optimization with the size optimization. Then it makes a comparison on the results of the strength analysis on the frame before and after optimization. The results show that the final optimization result meets the requirements, and the weight loss percentage is up to 34.3%. it is obvious that the effect of lightweight is remarkable.

cutting grass car frame; finite element analysis; topology optimization; size optimization

2016-08-13

國家自然科學基金資助項目(51675262)

陳遠帆(1991—)，男，江蘇常熟人，碩士研究生，主要從事車輛工程研究，E-mail:1761804372@qq.com。

陳遠帆，李舜酩，蘇玉青.拓撲優化與尺寸優化相結合的割草車車架輕量化設計[J].重慶理工大學學報(自然科學)，2017(1):28-35.

format：CHENG Yuan-fan, LI Shun-ming, SU Yu-qing.The Light-weight Design of the Cutting Grass Car Frame Combined the Topology Optimization with the Size Optimization[J].Journal of Chongqing University of Technology(Natural Science)，2017(1):28-35.

10.3969/j.issn.1674-8425(z).2017.01.005

TH12

A

1674-8425(2017)01-0028-08