嘗試運(yùn)用v—t圖像破解運(yùn)動(dòng)學(xué)問題
陳文月
中圖分類號(hào):G720 文獻(xiàn)標(biāo)識(shí)碼:A 文章編號(hào):1002-7661(2017)03-0002-03
在高中物理學(xué)習(xí)階段,面對茫茫“題海”中千“題”百怪、令人茫然不知所措的難題,不少人也許會(huì)產(chǎn)生頓挫之感。僅就運(yùn)動(dòng)學(xué)模塊而言,這類問題也隨處可見。不過,一旦熟練掌握并能夠巧用v-t圖像,其中的一些問題將會(huì)柳暗花明、迎刃而解,似乎算不上什么難題。
一、用v-t圖像求解最大速度
例1. 一輛從車站始發(fā)的汽車,做勻加速運(yùn)動(dòng),走了12s時(shí),司機(jī)發(fā)現(xiàn)還有乘客沒上來,于是立即做勻減速運(yùn)動(dòng)至停車,總共歷時(shí)20s,行進(jìn)了50m,求:(1)汽車的最大速度是多少?(2)開始減速前,該車已經(jīng)走過了多少路程?
此題只告訴了勻加速、勻減速的時(shí)間及最大的位移,但并沒有告知加速度的具體情況,顯然不能用Vt=Vo+at來簡單求證。但是,既然提供了“由車站始發(fā)”“勻加速”“勻減速”及最終“停車” 的“時(shí)間”“位移”等條件,我們就可以通過v-t圖像來加以解決,即:該汽車從“0”速度開始,在勻加速至12s時(shí),達(dá)到其最大速度(Vm),然后作勻減速運(yùn)動(dòng),至第20s時(shí),其速度減至最低速度(0),而其速度變化圖像與t軸圍成的三角形面積(S),則是該車行進(jìn)的距離(X),該三角形的頂點(diǎn)(h)即為該車的最大速度(Vm)。據(jù)此,繪出v-t圖如下: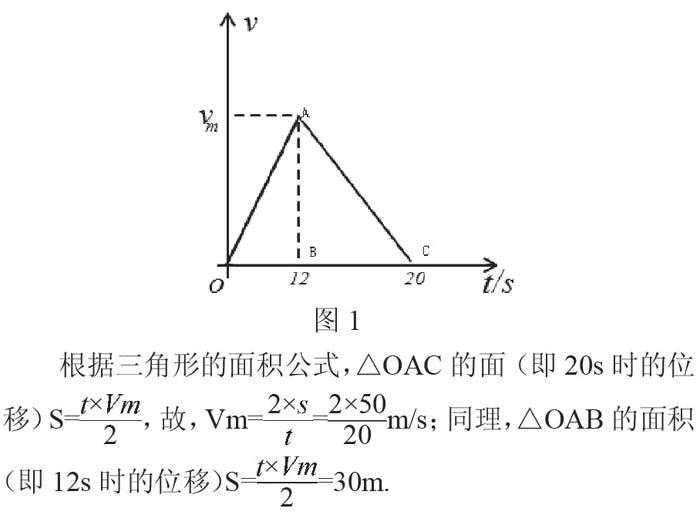
這樣,就用簡潔、明了的方式求得:該汽車的最大速度達(dá)到每秒5米,減速之時(shí)已經(jīng)行駛了30米。
二、通過v-t圖像比較時(shí)間長短
例2. 如圖2所示,ABC和DE是兩個(gè)高度相等的光滑斜面,ABC由傾角不同的兩部分組成,且AB+BC=DE,兩個(gè)相同的小球a、b分別從A點(diǎn)和D點(diǎn)沿兩斜面由靜止同時(shí)滑下,不計(jì)轉(zhuǎn)折處的能量損失,則滑到底部的先后次序是( )。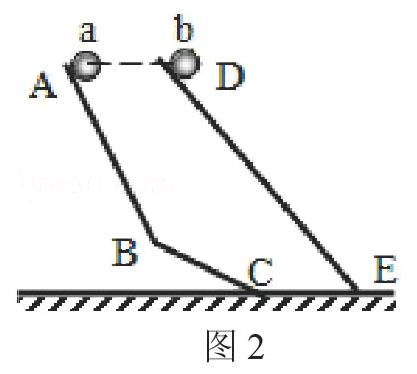
A.a球先到 B.b球先到
C.兩球同時(shí)到達(dá) D.無法判斷
判斷此題,切不可憑感覺用事。從題中所給的條件可知,兩球質(zhì)量相等,所處高度也相等,由此可直接得出的第一個(gè)推論是:兩球的重力勢能相等。而既然兩球的重力勢能相等,那么,按照機(jī)械能守恒定律,兩球在滑到底部時(shí),所做功相等,各自的動(dòng)能也相等。于兩球質(zhì)量相同,所以,可以得到的第二個(gè)推論是:兩球在滑動(dòng)到底部時(shí)的末速度(Vt)也就相等。另外,既然AB+BC=DE,所以,兩球在下滑過程中的位移相同。當(dāng)然,兩球都是從靜止?fàn)顟B(tài)釋放的,所以,各自的初速度均為Vo=0。明確了以上幾點(diǎn),就可以畫出兩球運(yùn)動(dòng)的如下v-t圖像: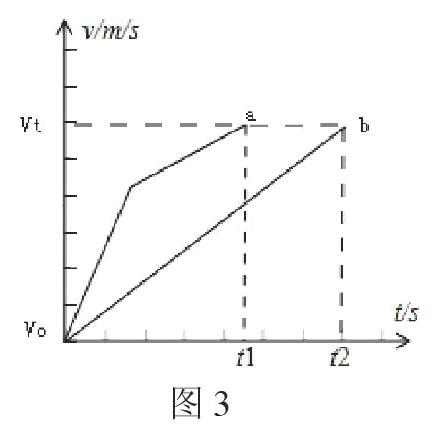
此v-t圖像根據(jù)題意(大致)表明,一開始(即AB段時(shí)),a球的加速度(即直線斜率)大于b,但到后來(即BC段時(shí)),其加速度(直線斜率)小于b;同時(shí),既然根據(jù)題意,AB+BC=DE,那么,圖像oat1所圍的面積要和obt2所圍的面積相等。從滿足這兩個(gè)條件的v-t圖像中不難直觀看出,a球下降所用的時(shí)間(t1)必然要比b球所用的時(shí)間(t2)短,故,答案為A,a球先到。
三、運(yùn)用v-t圖像判斷運(yùn)動(dòng)方式
例3.由甲地從靜止出發(fā),沿平直公路駛向乙地的一輛汽車,先以加速度a1做勻加速運(yùn)動(dòng),最后以加速度a2做勻減速運(yùn)動(dòng),中間可能有一段勻速運(yùn)動(dòng)過程,也可能沒有勻速運(yùn)動(dòng)過程,到乙地恰好停下。已知甲、乙兩地相距為s。試問:要使汽車從甲地到乙地所用的時(shí)間最短,汽車應(yīng)做怎樣的運(yùn)動(dòng)?
此題提供的信息要點(diǎn)有二:1.不論汽車采用什么樣的運(yùn)動(dòng)方式,甲乙兩地的距離是個(gè)定值,即汽車的位移為S;2.汽車的初速度和末速度均為0,而且不論采用什么運(yùn)動(dòng)方式,其最初和最后兩段距離的運(yùn)動(dòng)方式均有加速度,只不過最初為勻加速(a1),最后為勻減速(a2),兩者也不變。因此,可以直接按照滿足此條件的如下v-t圖像對各種運(yùn)動(dòng)方式進(jìn)行比較,看哪一種運(yùn)動(dòng)方式所用時(shí)間最短。時(shí)間最短者即為應(yīng)當(dāng)采用的運(yùn)動(dòng)方式。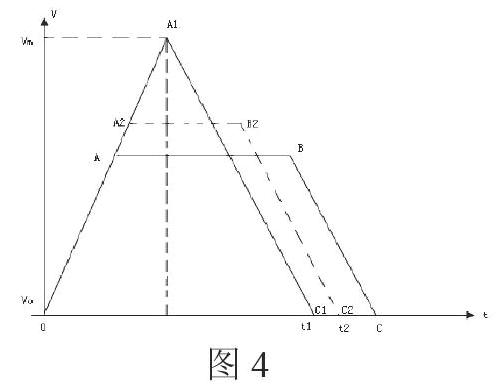
如圖4所示,設(shè)OABC所圍成的圖像表示甲乙兩地的距離S,根據(jù)題意,不論是采用先加速接著馬上減速的運(yùn)動(dòng)方式(如OA1線段與A1C1線段所示運(yùn)動(dòng)軌跡),還是先加速,然后勻速,接著再減速的運(yùn)動(dòng)方式(如OA2、A2B2與B2C2線段所示運(yùn)動(dòng)軌跡),△OA1C1的面積、梯形OA2B2C2 的面積,必須與梯形OABC的面積相等,而且,既然各種運(yùn)動(dòng)方式最初的加速度(a1)和最后的加速度(a2)均保持不變,這就意味著A1C1線段、B2C2線段均與BC線段保持平衡(斜率不變)。由此可以直觀的看出,采用“先加速接著馬上減速”的運(yùn)動(dòng)方式所用時(shí)間(t1)比先“加速然后勻速接著再減速”的運(yùn)動(dòng)方式所用時(shí)間(t2)要短,應(yīng)當(dāng)采用前者。
四、借助v-t圖像計(jì)算上升高度
例4. 一質(zhì)量為m = 40kg的小孩在電梯內(nèi)的體重計(jì)上,電梯從t=0時(shí)刻由靜止開始上升,在0到6s內(nèi),體重計(jì)示數(shù)F的變化如圖5所示。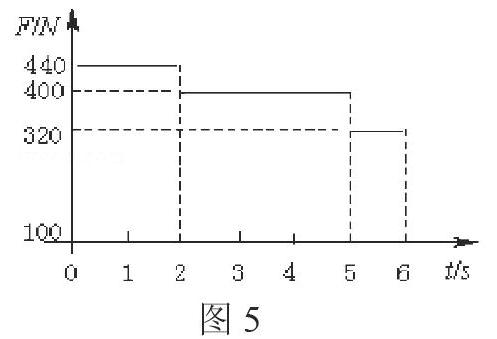
試問:在這段時(shí)間內(nèi)電梯上升的高度是多少?取重力加速度g=10m/s2。
解答此題,首先應(yīng)當(dāng)明確的是,小孩的重力mg=400=400N;當(dāng)其乘坐電梯上升時(shí),如果電梯的上升是勻速的,體重計(jì)的示數(shù)就保持不變,應(yīng)為400N。但當(dāng)電梯加速時(shí),由于超重,體重計(jì)的示數(shù)會(huì)顯示高于400N,相反,當(dāng)減速時(shí),體重計(jì)的示數(shù)則會(huì)顯示低于400N,而且,只要是進(jìn)行勻加速或勻減速,該增加或減少的數(shù)值也會(huì)保持恒定。據(jù)此觀察體重計(jì)示數(shù)F的變化圖可知,第一,在最初的2s內(nèi),電梯是由靜止開始進(jìn)行勻加速上升的(示數(shù)計(jì)讀數(shù)高于400N而且恒定);第二,在隨后的第2至第5s內(nèi),電梯是勻速上升的(示數(shù)讀數(shù)等于400N);第三,在最后1s內(nèi)(第6秒內(nèi)),電梯開始進(jìn)行勻減速(上升)直到停止(即電梯上升的最高點(diǎn))。
問題是,電梯及小孩上升的加速度(a1)、勻速上升的速度(vt)以及勻減速時(shí)的加速度(a2)究竟是多少呢?
根據(jù)牛頓第二定律,F(xiàn)合=ma1,即,440-400=401,由此得知,電梯勻加速上升的加速度a1=1m/s2。同理,電梯勻減速上升時(shí),320-400=40€譨2,故,勻減速上升時(shí)的加速度a2= -2m/s2。根據(jù)Vt=Vo+at可知,在電梯上升的第2至第5s內(nèi),其勻速上升的速度(即第2s末的速度)Vt=0+(1)=2m/s。
將上述結(jié)論轉(zhuǎn)換為電梯及小孩的v-t運(yùn)動(dòng)圖像,則有下圖6:
五、小結(jié)
綜上可見,用v-t圖像求解運(yùn)動(dòng)學(xué)模塊的有關(guān)問題,有時(shí)可以簡化解題的過程,化繁為簡,具有直觀、形象、簡明的特點(diǎn)。其實(shí)質(zhì)是把復(fù)雜的物理量之間的代數(shù)關(guān)系轉(zhuǎn)化為幾何關(guān)系,核心是通過速度圖線與時(shí)間t軸圍成的面積來加以比較、計(jì)算或分析。因此,運(yùn)用這一方法,首先應(yīng)當(dāng)認(rèn)真審題,切不可遺漏條件。除了要注意把握題目明確給定的條件(如時(shí)間、質(zhì)量、位移、長度,初速度、末速度狀態(tài))外,還要仔細(xì)發(fā)掘題目中隱含的問題。比如,例4中的加速度a1、a2及勻速上升的速度,例2中a、b兩球的末速度等。其次,在將物理量轉(zhuǎn)化為V-t圖像時(shí),必須時(shí)刻牢記,該圖像圍成的幾何面積實(shí)際上表示的只是運(yùn)動(dòng)學(xué)上的位移或者距離,必須對幾何學(xué)中的基本公式、定理(如三角形的面積、梯形的面積公式計(jì)算等)熟爛于胸。再次,在v-t圖轉(zhuǎn)化中,尤其要注意速度線段的曲與直、傾斜度、等高線、起始點(diǎn)。只有勻速或勻加速運(yùn)動(dòng)才能轉(zhuǎn)化為直線,只有在具有加速度的運(yùn)動(dòng)中,該直線才有斜率,而且加速度越大,斜率越大。而v-t圖像中的等高線,則意味著速度相等,當(dāng)然,速度線段與t軸相交的地方,也意味著速度相等(0)。最后,v-t圖像的運(yùn)用和物理學(xué)的相關(guān)內(nèi)容緊密相關(guān),如果物理學(xué)的基礎(chǔ)不扎實(shí),就勢必嚴(yán)重影響到v-t圖像法在運(yùn)動(dòng)學(xué)問題上的科學(xué)運(yùn)用。比如,如果對動(dòng)能定理、機(jī)械能守恒定理認(rèn)識(shí)模糊,就不可能對例2問題進(jìn)行v-t圖的準(zhǔn)確轉(zhuǎn)化;如果對牛頓第二定律沒有真正領(lǐng)會(huì),就不可能對例4問題的加速度用精準(zhǔn)的斜線進(jìn)行表示。

