立體庫作業均衡及貨位優化仿生算法研究

杜永華，項 前，呂志軍，陳 東

（1.東華大學 機械工程學院，上海 201620；2.上海精星物流設備有限公司，上海 201611）

立體庫作業均衡及貨位優化仿生算法研究

杜永華1，項 前1，呂志軍1，陳 東2

（1.東華大學 機械工程學院，上海 201620；2.上海精星物流設備有限公司，上海 201611）

在批量訂單的情況下，為了提高自動化立體倉庫（AS/RS）的整體作業效率，提出了以堆垛

貨位優化；作業均衡；作業效率；二進制粒子群算法；遺傳算法

0 引言

自動化立體倉庫（AS/RS）由于具有空間利用率較高、入出庫能力較大、管理較智能化等優點，己成為現代企業生產管理中不可缺少的組成部分[2]。貨位分配是影響立體倉庫工作效率高低、揀選成本高低的一大主要因素，因此為了提高自動化立體庫的性能，對倉儲貨位優化的研究越來越引起人們的重視。研究主要從兩方面展開，一方面從分配策略或貨位分區方面進行研究，文獻[3]給出一種基于BOM（Bill of Material）分類的貨位優化方法；文獻[4]通過對產品頻度和偏離度的研究，來實現出入庫貨位的優化；文獻[4～6]則運用分區的策略來實現貨位優化。另一方面建立貨位優化數學模型，主要通過仿生算法來對模型進行優化求解，文獻[6,7]分別運用貪婪算法、非支配遺傳算法，以存儲能耗、貨架穩定性、運行效率為目標對立體倉庫貨位分配進行優化；文獻[8]以存耗低、運行時間短為目標，運用離散粒子群算法來實現立體庫貨位優化。可以看出，上述貨位優化研究大多集中在策略研究或者以路徑、能耗及時間為目標的優化，但是在進行批量出入庫操作時，由于各巷道作業的不均衡容易造成一些堆垛機閑置或超負荷運作，從而導致揀選效率和揀選質量的下降、資源的閑置，這顯然不能滿足批量作業的實際情況。另外，以上仿生算法的運用主要表現為遺傳算法（Genetic Algorithm，GA）與粒子群算法（Particle Swarm Optimization），對二進制粒子群算法（Binary Particle Swarm Optimization，BPSO）的運用較少。據此，在批量訂單操作中，本文提出了以堆垛機作業均衡以及工作效率高為目標的優化模型，與標準遺傳算法比較，設計了一種基于二進制粒子群的模型求解仿生算法。

1 問題描述與數學模型

1.1 問題描述

所研究的貨位優化問題可描述如下：在一個K排R層C列的儲存區（其簡易圖如圖1所示）進行批量出庫或者入庫操作，每張訂單中的貨物需要通過所處巷道堆垛機來實現出入庫，當堆垛機執行完最后一個任務后返回到出入庫臺[9]。其中，每個巷道的堆垛機同時工作，堆垛機的工作效率通過其運行路徑來衡量，每個巷道堆垛機的作業均衡也由該巷道堆垛機的運行路徑來衡量。

圖1 儲存區簡易圖

1.2 數學模型

任意一個貨位b均可用一個六元組（kb,rb,cb,Mb,Qb,Sb）表示，其中：（kb,rb,cb）表示貨位b的坐標即（排，層，列），Mb表示貨位b上所存貨物的品項號，Qb表示貨位b上所存貨物的數量，Sb表示貨位b的狀態（有四種狀態：任務完成、任務失敗、任務正在執行、任務懸掛，默認的狀態是任務完成）。

每次任務T可用如下向量表示：

其中每張訂單中的一個品項表示一個任務Ti，j=（Md, Qd），Md表示所需貨物的品項號，Qd表示所需貨物的數量。

為了讓問題的復雜度降低，同時結合實際情況，做出如下模型假設：1）每次任務向量T都是單純的出庫或者入庫；2）倉庫里貨物的品項和數量能夠充分滿足訂單需求，且一個貨位只能滿足一個任務；3）堆垛機操作每個品項所用時間相等，且每趟只對一個目標儲位進行操作；4）每個儲位只能存放一個貨物單元（托盤或集裝箱）[11]，并且在作業之前對每個貨位的狀態（任務執行完成、任務失敗、任務正在執行、任務懸掛，默認每個貨位狀態都是任務執行完成）、儲位上品項信息（品項、數量、規格等）已知。

以堆垛機作業行程均衡和運行效率為目標建立優化模型，具體如下：

式中：i為巷道號，i = 1，2，…，I；Ni為巷道i中目標貨位的集合；N為倉庫中可行貨位（根據任務所需的品項并且貨位的狀態是任務完成來確定）的集合；K為倉庫中貨架總的排數；R為倉庫中每排貨架總的層數；C為倉庫中每排貨架總的列數；j為粒子位索引號，j = 1，2，…，J；Length（xj=1）表示粒子中粒子位為1的個數；Length（T）為任務向量中任務的的個數；Length（xi,j=1）表示粒子中粒子位所對應的貨位號位于巷道i且該粒子位為1的個數；Length（Ti）為每個任務中的貨物品項號位于巷道i的任務個數S為各巷道工作行程的平均值；D為各個巷道工作行程的最大值；P為懲罰函數。

模型以最小化巷道工作行程（即最高的效率）以及各個巷道堆垛機工作量均衡為目標。約束(7)表示最后揀選的貨位數與任務數相等；約束(9)表示具體到每一個巷道的任務數和該巷道揀選的貨位數相等；懲罰系數(8)、(10)運用靜態懲罰函數的方法來處理約束(7)、(9)[13]，對于約束(7)、(9)將其違反程度分為2個等級，不同等級采用不同懲罰系數。

2 基于二進制粒子群算法的模型求解

因為動態貨位優化是一個離散型優化問題，所以適用于Kennedy和Eberhart提出的二進制粒子群算法（BPSO）[12]。基于BPSO的貨位編碼、解碼及算法求解過程描述如下：

1）貨位編號

給每個貨位采取實數編號，從1開始，則每個貨位的編號可以表示為：

式(11)中C和R表示的是每排貨架總的列數、層數，（k，c，r）為當前貨位的位置坐標。

2）粒子解碼

圖2 解碼實例

BPSO中粒子位只有0和1兩種，所以先根據任務向量中品項編號、每個貨位的狀態來確定可行域，讓可行域的長度和粒子維度相等。粒子上相應的粒子索引號與可行域相應的貨位索引是一一對應的，當該粒子位上是1時就表示相對應的貨位被選中，反之就表示該貨位沒被選中。

則最后所選擇的貨位為15、20、77、89。

基于二進制粒子群的模型基本求解過程如下：

begin

確定可行貨位N（根據任務所需的品項并且貨位的狀態是任務完成）；

參數值（主要有：種群規模（M）、粒子維度、學習因子c1、c2值、最大迭代代數等）的初始化；

t←0；

將每個可行貨位采用二進制編碼，初始化粒子群P（t）中每個粒子的位置、速度和個體極值；

while（not termination condition）do

for j←1 to M do

將每個粒子（xj）解碼（具體見解碼過程）成貨位信息（Nj）；

計算目標函數值F(Nj)、F(pbestNj)、F(gbestNj)；

將貨位信息（Nj）、當前最好解的貨位信息（pbestNj）以及近鄰中最好解的貨位信息（gbestNj）分別編碼（解碼的逆過程）成粒子信息（xj）、當前最好的解粒子信息（pbestj）和近鄰中最好解粒子信息（gbestj）

其中，N為可行貨位的集合；Nj為可行貨位中被選中的貨位；t表示迭代次數；P(t)表示第t次迭代時的粒子群；pbestNj為j粒子當前發現的最好解貨位；gbestNj為j粒子的近鄰當前所發現的最好解貨位；pbestj為j粒子當前所發現最好的解粒子；gbestj為j粒子的近鄰當前所發現的最好解粒子；Vj為粒子群中第j個粒子的速度；函數F( )表示計算粒子的目標函數值；rand( )為屬于（0，1）內的一個隨機數； S（v）是sigmoid函數具體的表達式為：

3 試驗及分析

為了驗證優化模型的有效性，研究設計了基于BPSO和GA的模型求解仿生算法，以VS為編程環境，進行了多品項出庫作業，最后對兩種算法的優化結果做了對比和分析。試驗對象為6排6層8列貨架組成的單庫型區域，有三條揀貨巷道。因為進行批量出庫或批量入庫的時候其可行域的確定、優化模型基本都一致，所以試驗中的任務向量設定為出庫任務T，具體如下所示：

3.1 參數的確定

通過在不同種群規模下目標函數值的對比試驗，來選取種群規模數，當種群規模小于100時，其目標函數值有明顯減小的趨勢，當種群規模大于100時又有上升，而種群規模等于100的時候目標函數值最小，所以種群規模選擇100。具體的變化如圖3所示，其中所用到的任務向量為出庫任務向量T，并且每次的學習因子相同。

圖3 不同種群規模目標函數值的對比（每種規模試驗10次）

試驗中用到的遺傳算法（GA）是標準的遺傳算法，具體的算法參數設置詳情如表1所示。

表1 試驗案例算法參數設置

3.2 不同優化方法的試驗結果對比

試驗中任務向量為出庫任務向量T，圖4、圖5分別表示的是經過BPSO、GA優化后，目標函數值的迭代情況，它們優化結果對比如表2所示。

圖4 基于BPSO的目標函數值迭代情況

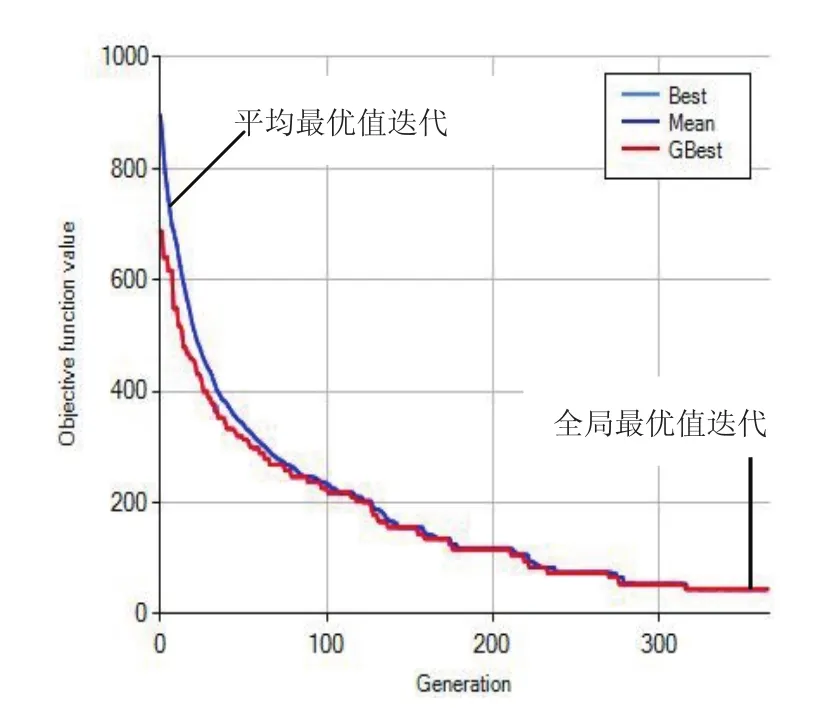
圖5 基于GA的目標函數值迭代情況

表2 BPSO與GA的優化結果對比

在立體庫中每個巷道的堆垛機是并行作業的，所以每次任務所用時間取決于行程值最大的那個巷道，因此可以通過巷道的行程來表示作業效率。由圖4、圖5以及表2可以看出基于二進制粒子群和標準遺傳的仿生算法對模型的求解都能取得較好的結果，BPSO經過245代后可得到目標函數值10.28、堆垛機行程均衡值B11為0.022及行程值D13為41.05，GA經過316代后可得到目標函數值31.47、堆垛機行程均衡值B12為3.55及行程值D23為75.21，顯然BPSO比GA具有如下四點優勢：1）可以以較少的代數得到較好的目標函數值；2）每代的種群差異較大，全局搜索能力更強；3）因為B11遠小于B12，各堆垛機作業更加均衡；4）工作效率η提高了45.42%。通過以上分析，基于二進制粒子群算法求解的模型較符合實際的批量訂單操作，提高了倉儲作業的整體效率和質量。

4 結束語

在進行批量出入庫時，為了提高倉儲整體作業效率，提出了基于二進制粒子群的堆垛機作業均衡及貨位優化模型，并且與標準遺傳算法進行了優化效果對比，通過試驗驗證了模型及算法的有效性。由于本文只局限于單純出庫或入庫作業研究，后續研究將針對出入庫混合作業各巷道均衡性進一步展開。所研究的基于二進制粒子群的作業均衡以及貨位優化模型及仿生算法已經在企業倉儲管理系統中得到了應用，并取得了良好地成效。

參考文獻：

[1] 丁立言,張鐸.倉儲自動化[M].1版.北京:清華大學出版社,2002,14-28.

[2] Hsieh S,Tsai K C. A BOM oriented class-based storage assignment in an automated storage/retrieval system[J]. International Journal of Advanced Manufacturing Techology,2001,17(9):683-691.

[3] 穆聰聰,郭敏.基于產品頻度與偏離度的貨位分配策略研究[J].物流科技,2015,06:107-112.

[4] T. A. Ajol, Ismail I, S. S. Gran, et al. An enhanced storage location assignment policy by minimizing handling cost for warehouse XYZ[A].International Conference on Computer, Communications, and Control Technology[C].IEEE,2015.

[5] Park B C, Foley R D, Frazelle E H. Performance of miniload systems with two-class storage[J].European Journal of Operational Research,2006,170(1):144-155.

[6] 張思建,方彥軍,賀瑤,肖勇.基于模擬退火算法的AVS/RS多批貨箱入庫貨位優化[J].武漢大學學報(工學版),2016,02:315-320.

[7] 李珍萍,于洋濤,李文玉.基于貪婪算法的倉庫貨位優化問題研究[J].物流技術,2015,05:242-244.

[8] 印美,洪榮晶,劉林.基于非支配遺傳算法的自動化倉庫動態貨位優化[J].組合機床與自動化加工技術,2015,03:31-34+37.

[9] Li H P, Fang Z F, Ji S Y. Research on the Slotting Optimization of Automated Stereoscopic Warehouse Based on Discrete Particle Swarm Optimization[A].IEEE the, International Conference on Industrial Engineering and Engineering Management[C].2010:1404-1407.

[10] 李曉,項前,呂志軍,管樹林.基于單雙親混合GA的復雜揀選作業優化[J].計算機工程與設計,2015,12:3359-3364.

[11] 張小川.現代倉儲物流技術與裝備[M].北京:化學工業出版社,2013:37-38.

[12] 鄧雪,李家銘,曾浩健,陳俊羊,趙俊峰.層次分析法權重計算方法分析及其應用研究[J].數學的實踐與認識,2012,07:93-100.

[13] 黃競偉,朱福喜,康立山.計算智能[M].1版.北京:科學出版社,2010,6.

[14] Kennedy J,Eberhart R. A.discrete binary version of the particle swarm algorithm[A].Proceeding of the World Multiconference on Systemics,Cybernetics and Informatics[C].New Jersy:Piscatawary,1997,4104-4109.

Bionic algorithm research on AS/RS operation balance and location assignment optimization

DU Yong-hua1，XIANG Qian1，LYU Zhi-jun1，CHEN Dong2

TP18

：A

1009-0134(2017)01-0122-05

2016-09-11

上海市自然科學基金資助項目（15ZR1400600）；2015松江區產學研創新項目計劃

杜永華（1992 -），男，湖南邵陽人，碩士研究生，研究方向為智能制造。

機作業均衡與高倉儲效率為目標的立體庫貨位優化模型。設計了基于二進制粒子群（Binary Particle Swarm Optimization，BPSO）和遺傳算法（Genetic Algorithm，GA）的模型求解仿生算法。通過同一個立體庫批量訂單作業實例，驗證了所提模型及算法的有效性，算法試驗及分析表明，基于BPSO的立體庫作業均衡及貨位優化效果較遺傳算法顯著。