基于修正黏性摩擦LuGre模型的比例多路閥摩擦補償

陳東寧 劉一丹 姚成玉 蔣棟林 王可勛1．燕山大學河北省重型機械流體動力傳輸與控制實驗室，秦皇島，0660042．先進鍛壓成形技術與科學教育部重點實驗室(燕山大學)，秦皇島，066004．燕山大學河北省工業計算機控制工程重點實驗室，秦皇島，066004

基于修正黏性摩擦LuGre模型的比例多路閥摩擦補償

陳東寧1,2劉一丹1,2姚成玉3蔣棟林1,2王可勛1,2
1．燕山大學河北省重型機械流體動力傳輸與控制實驗室，秦皇島，0660042．先進鍛壓成形技術與科學教育部重點實驗室(燕山大學)，秦皇島，0660043．燕山大學河北省工業計算機控制工程重點實驗室，秦皇島，066004

為減小摩擦對比例多路閥性能的影響，提出基于修正黏性摩擦LuGre模型的比例多路閥摩擦特性分析、模型參數辨識以及摩擦補償方法。通過實驗測試間接得出摩擦數據，運用數據擬合方法辨識出修正黏性摩擦LuGre模型的靜態和動態參數。基于辨識參數設計出修正黏性摩擦LuGre模型摩擦狀態觀測器，將觀測器摩擦信號輸出量反饋到控制模型輸入端，減小摩擦對比例多路閥性能的不良影響。仿真結果表明，基于辨識參數的修正黏性摩擦LuGre模型摩擦補償方法可提高比例多路閥的位置跟蹤精度。

比例多路閥；摩擦補償；LuGre模型；黏性摩擦；參數辨識

0 引言

摩擦是影響比例多路閥靜動態性能的重要因素，是造成閥芯卡澀卡滯、低速爬行、流量滯環大、極限環振蕩以及微動特性差等現象的主要原因，尤其在閥芯開啟、關閉以及閥芯換向時摩擦的影響最為嚴重[1-2]。比例多路閥特性直接關系到液壓系統的運行性能，因此，對比例多路閥進行摩擦特性分析和摩擦補償的研究具有重要意義。

目前摩擦補償的方法主要有基于摩擦模型的補償、不依賴于摩擦模型的補償、基于智能控制策略的摩擦補償以及復合控制策略的摩擦補償等。常用的摩擦模型有庫侖摩擦模型、Stribeck摩擦模型、LuGre摩擦模型等。為了消除摩擦不穩定現象，一個精確的摩擦模型是必要的，一個好的摩擦模型需集成多個摩擦問題研究中的重要現象[3]。由于LuGre模型能夠全面、精確地描述預滑動位移、摩擦滯環、變化的臨界摩擦、爬行以及Stribeck效應等各種摩擦靜動態特性，故已成為當前摩擦補償最常采用的一種摩擦模型[4-6]。文獻[7]提出了一種一次性獲得模型所有參數的新型快速識別方法，求解出了相應的LuGre離散遞推方程，解決了參數辨識時無法有效檢測鬃毛微位移的難題。文獻[8]提出在運動逆轉和運動停止時，與滯后相關的摩擦阻尼是作為精確定位控制最重要的部分，對摩擦的效果起到很關鍵的作用。文獻[9]對比了基于LuGre摩擦模型和基于經典庫侖+黏滯摩擦模型計算所得的泵柱塞彈性位移，結果表明，基于LuGre摩擦模型計算得到的抽油泵泵效更接近生產實際。文獻[10]根據LuGre模型，構造了一個非線性觀測器來估計摩擦，減小了摩擦對伺服系統性能的影響。文獻[11]針對LuGre摩擦模型參數耦合動態參數辨識困難等問題，提出了一種基于區間分析的LuGre摩擦模型動態參數辨識方法。文獻[12]通過李雅普諾夫穩定性分析方法，設計了基于LuGre模型的非線性摩擦自適應補償算法，在線辨識出摩擦模型參數，并據此構造了雙閉環狀態觀測器，補償機電伺服系統所受的摩擦。文獻[13]根據實驗平臺速度較高時，隨速度增加摩擦增長趨勢減緩的現象，建立了修正黏性摩擦的LuGre模型。

本文針對負載敏感比例多路閥提出了一種基于修正黏性摩擦LuGre模型的固定參數摩擦補償方法。比例多路閥中使用的增加顫振信號的方法在顫振頻率和幅值選取合適時可在一定程度減小摩擦對閥芯運動特性的不利影響，但該方法沒有考慮摩擦與閥芯速度之間的關系，補償效果有待提高。為此，本文首先通過實驗的方法求解閥芯所受摩擦與閥芯速度的關系，進而研究基于修正黏性摩擦LuGre模型的比例多路閥摩擦補償方法并進行仿真分析，以提高比例多路閥的位置跟蹤精度。

1 比例多路閥實驗測試

由于通過實驗無法直接測試負載敏感比例多路閥閥芯摩擦，故需要通過采集實驗數據進行摩擦的間接計算，獲得摩擦與閥芯運動位移、運動速度以及加速度之間的關系數據。比例多路換向閥可以由多聯組成，現對一聯進行測試，實驗測試液壓系統原理如圖1所示。

1.蝶閥 2.變量泵 3.電機 4.換向閥 5.標準阻尼元件6.三通流量補償器 7.安全溢流閥 8.三通減壓閥9.節流閥 10.流量計 11.測壓接頭 12.比例減壓閥13.比例多路閥換向塊 14.梭閥 15.二通流量補償器16.插裝式二次溢流閥 17.壓力傳感器 18.比例溢流閥19.冷卻器 20.位移傳感器圖1 實驗測試液壓系統原理圖Fig. 1 Schematic diagram of experimental test

實驗測試系統主要有三條油路。第一路：變量泵2出來的壓力油，經比例溢流閥18調定壓力后經過二通流量補償器15，使換向閥主閥口的壓差恒定為0.6 MPa。壓力油進入主閥P口，A、B口為負載口，回油經冷卻器19流回油箱。第二路：壓力油進入三通流量補償器6，該閥與梭閥14配合，使泵出口壓力比最大負載壓力始終高0.9 MPa。第三路：壓力油進入三通減壓閥8，為比例減壓閥12提供2.5 MPa的先導控制油，再經比例減壓閥，為主閥芯提供控制油壓力。

比例多路閥主閥結構如圖2所示。實驗測試主閥及傳感器連接如圖3所示。

1.比例電磁鐵 2.外彈簧 3.內彈簧 4.主閥控制腔5.比例減壓閥 6.主閥芯 7.閥體 8.手柄圖2 多路閥主閥結構Fig. 2 Main valve structure of the multi-way valve

圖3 實驗測試照片Fig. 3 Photograph of experimental test

利用HPM便攜式數據采集儀采集各油口的壓力數據，利用NI數據采集卡采集輸入電流、閥芯位移、流量數據。根據實驗測試要求利用LabVIEW實現控制信號輸入、數據采集、測試曲線顯示以及數據存儲等功能。

實驗采集的數據往往帶有噪聲信號，在對采集數據進行理論分析前，需要去除噪聲信號，將有用信號提取出來。采用小波變換進行數據消噪。圖4、圖5為對2.2～2.3 V(階躍值0.1 V)階躍控制信號P口油液壓力數據消噪前后時域對比圖,圖6、圖7為消噪前后頻域對比圖。

圖4 原始數據的壓力信號時域圖Fig. 4 Time-domain diagram of original pressure signals

圖5 消噪后的壓力信號時域圖Fig. 5 Time-domain diagram of de-noised pressure signals

圖6 原始數據的信號功率譜密度Fig. 6 Power spectral density diagram of original signals

圖7 消噪后的信號功率譜密度Fig. 7 Power spectral density diagram of de-noised signals

數據消噪后，通過采集的數據進行摩擦的間接計算。由于閥芯開啟時微動特性的影響，閥芯加速度較小，瞬態液動力較小，故將其忽略。主閥芯上的力主要有驅動力、內外彈簧作用力、穩態液動力、慣性力以及摩擦力等，其力平衡表達式為

(1)

式中，Fi為驅動力;m為主閥芯等效質量;x為閥芯位移;Fbs為閥芯穩態液動力;Ft為內外彈簧的作用力;Ff為摩擦力。

通過對各傳感器采集來的信號進行處理和計算，應用式(1)求出摩擦數據。

2 修正黏性摩擦LuGre模型的參數辨識

在獲取大量實驗數據的基礎上，對比例多路閥摩擦進行基于修正黏性摩擦LuGre模型的參數辨識，得出摩擦與閥芯速度的關系。

2.1 LuGre模型

LuGre摩擦模型把兩個剛體間的接觸假定為粗糙面間的接觸，將這種接觸形象地表述為兩剛體通過彈性鬃毛的接觸，當施加外力時，接觸表面近似彈性鬃毛的作用力表現為一種類似彈簧的彈性力，將微觀鬃毛的變形簡化為用一個彈簧和一個阻尼組成的簡單系統來分析[14]，模型結構如圖8所示。

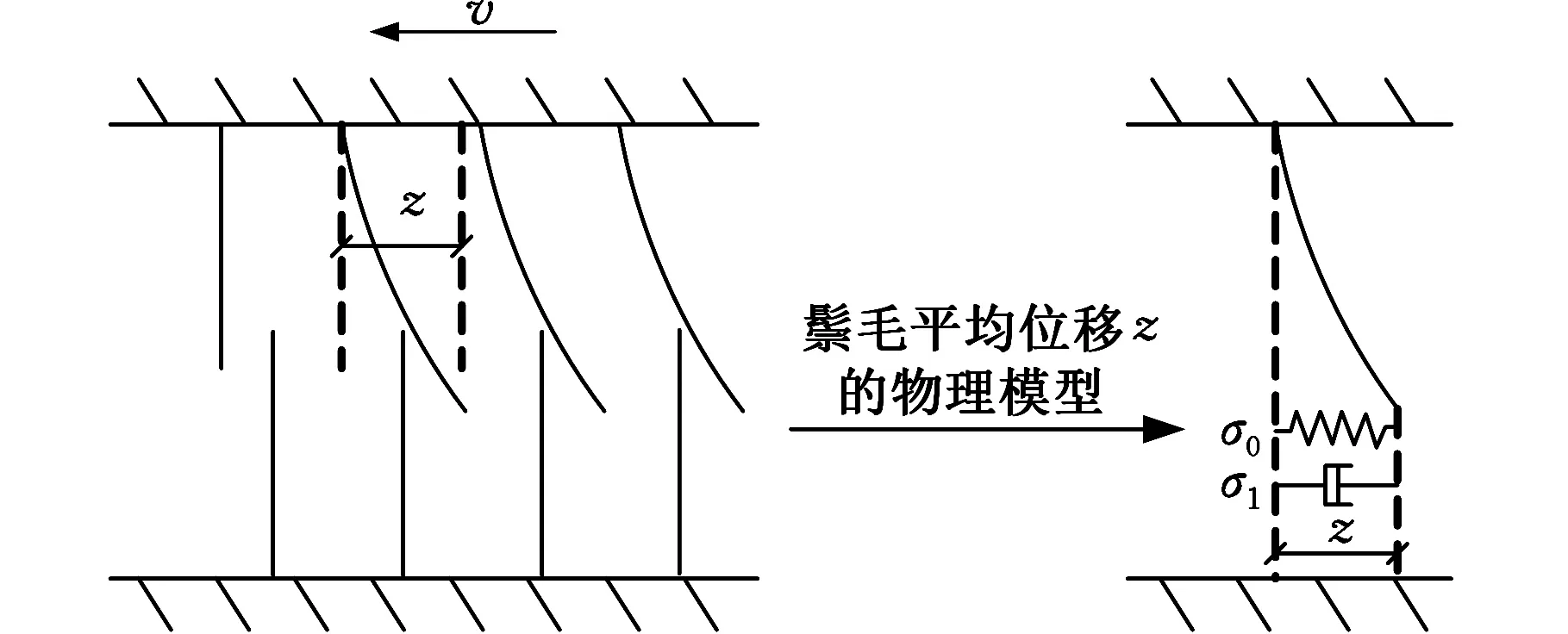
圖8 LuGre摩擦模型結構示意圖Fig. 8 Structure diagram of the LuGre model

摩擦力Ff可以用LuGre模型描述為

(2)

(3)

σ0g(v)=Fc+(Fs-Fc)e-(v∕vs)2

(4)

式中,σ0為鬃毛的剛度系數；z為鬃毛的平均位移；σ1為阻尼系數；σ2為黏性摩擦系數；v為剛體相對運動速度；Fc為庫侖摩擦力；Fs為靜摩擦力；vs為Stribeck效應速度；g(v)為大于0的函數，且有界。

當系統處于穩態，即dz/dt=0時，鬃毛的穩態平均位移zss為

(5)

穩態摩擦力Fss和速度v的關系表示為

Fss(v)=σ0g(v)sgn(v)+σ2v=
Fcsgn(v)+(Fs-Fc)e-(v/vs)2sgn(v)+σ2v

(6)

式中，σ2、Fc、Fs、vs為靜態參數，σ0為動態參數。

2.2 修正黏性摩擦LuGre模型

從式(2)可以看出，LuGre模型摩擦力包括三部分，前兩部分屬于非黏性摩擦部分，最后一部分屬于黏性摩擦部分。在高速階段，LuGre模型中的黏性摩擦部分是與速度成線性關系的。而實際高速階段黏性摩擦部分有隨著速度增大其增長趨勢減緩的現象，因此應用修正黏性摩擦的LuGre模型。該修正模型可表述為

(7)

(8)

σ0g(v)=Fc+(Fs-Fc)e-(v∕vs)2

(9)

式中，σ3為黏性摩擦斜率因子；σ4為黏性摩擦變化因子。

σ3、σ4、Fc、Fs、vs是待辨識的靜態參數。σ0、σ1為待辨識的動態參數。上述摩擦模型描述了摩擦接觸面內部不可測量狀態變量z的動態特性，狀態變量z可描述邊界潤滑摩擦過程中摩擦接觸面的相對變形。

2.3 基于非線性最小二乘法的靜態參數辨識

非線性最小二乘法是以誤差的平方和最小為準則來估計非線性模型參數的一種方法。據非線性最小二乘法理論，對計算獲得的摩擦力和速度數據進行曲線擬合。在擬合前需要對各靜態參數初始值進行設置，以使擬合效果最佳，Stribeck速度vs為實驗曲線最低點所對應速度；閥芯的相對運動速度在vs以上時，摩擦力與相對運動速度之間關系近似為一條直線；直線在y軸的截距近似為庫侖摩擦力Fc的值；斜率近似為黏性摩擦系數σ2的值；最大靜摩擦力Fs為主閥芯零速時的摩擦力。分別對LuGre模型和修正黏性摩擦LuGre模型進行參數識別，如圖9所示。

(a)LuGre模型

(b)修正黏性摩擦LuGre模型圖9 摩擦力與閥芯速度曲線Fig. 9 Curves of friction according to the spool velocity

從圖9中可以看出，修正黏性摩擦LuGre模型在曲線最低點處(Stribeck效應速度)的擬合效果比LuGre模型的擬合效果好。在較高速度階段(0.6～0.87 mm/s)時，修正黏性摩擦LuGre模型的擬合效果也比LuGre模型的擬合效果好，它反映了閥芯速度較高時摩擦力隨速度增大其增長趨勢減緩的特性，對摩擦力的估計更為準確。

LuGre模型和修正黏性摩擦LuGre模型辨識參數對比如表1所示。

表1 兩種模型靜態辨識參數對比
Tab.1 Comparison of two models’ static identification parameters

模型Fc(N)Fs(N)vs(mm/s)σ2(N·s/mm)σ3(N)σ4(s/mm)LuGre15.12520.02559修正黏性摩擦LuGre7.54565.420.02849.732.875

2.4 修正黏性摩擦LuGre模型動態參數辨識

模型的兩個動態參數σ0和σ1從物理意義上講，σ0是LuGre模型鬃毛的剛度系數，σ1是模型的阻尼系數，兩參數與閥芯運動位移相關。在預滑動階段，摩擦力表現為與閥芯相對運動位移的關系，將鬃毛模型中的平均位移z近似為閥芯的位移x，即

(10)

在閥芯微小位移內，忽略鬃毛微小變形所產生的彈性力變化；在實驗測試時發現換向過程中流量傳感器檢測到的流量變化非常微小，故忽略液動力的影響；由于在微滑動階段慣性力很小，故也將其忽略。輸入的驅動力主要克服摩擦的影響，所以可以建立力平衡公式為

σ0x+σ1v+σ3(1-e-σ4v)=Fi

(11)

式(11)第三項中參數σ3、σ4已經獲得，因此只需要辨識σ1和σ0。對主閥進行微動特性實驗研究，采集閥芯0.01～0.08 mm微小位移下的實驗數據，通過研究小階躍信號下密封材料發生微小變形時摩擦力的變化，來獲得相應動態摩擦參數，得出σ0= 60.56 N/mm、σ1=473 N·s/m。

3 基于修正黏性摩擦LuGre模型的摩擦補償

AMESim軟件為多學科領域復雜系統建模仿真平臺，其內置液壓庫可用于建立比例減壓閥、主閥、負載液壓缸等模型，并且可以設置主閥閥芯的摩擦力參數。Simulink軟件基于模型框圖的圖形用戶界面，可使修正黏性摩擦LuGre模型狀態觀測器的設計更加簡潔便利。為此，利用AMESim和Simulink聯合仿真技術對比例多路閥進行摩擦補償的建模與仿真。

3.1 摩擦補償控制器設計

基于修正黏性摩擦LuGre模型的摩擦補償控制原理如圖10所示。

圖10 摩擦補償控制框圖Fig.10 Control block diagram of friction compensation

圖10中摩擦觀測器根據主閥位移和誤差對實際摩擦力進行估計，摩擦力估計值作為摩擦補償量，前饋補償根據期望位置信號計算前饋補償量，H(s)控制環節根據位置誤差信號計算誤差補償量[15]，從而有：控制量等于前饋補償部分與H(s)控制器輸出及摩擦補償之和。

定義位置跟蹤誤差為：δ=y-r，位置誤差系數為k0,由于摩擦模型中的鬃毛形變量不可直接測量，需要通過設計摩擦狀態觀測器進行評估[16],因此設計鬃毛觀測器如下：

(12)

從而有摩擦觀測器如下：

(13)

設計系統控制律如下：

(14)

其中，mts2r是前饋補償，控制器H(s)采用下式:

H(s)=kP+kDs+kI/(τs+1)

(15)

式中，kP、kI、kD分別為比例、積分、微分系數。

3.2 比例多路閥AMESim參數化建模

構建比例多路閥結構參數化AMESim模型，如圖11所示。

圖11 比例多路閥AMESim仿真模型Fig.11 AMESim simulation model of the proportional multi-way valve

3.3 摩擦觀測器的建模

根據修正黏性摩擦LuGre模型式(7)～式(9)，利用Simulink搭建摩擦狀態觀測器，如圖12所示。

將摩擦補償控制器的模型封裝后，加入到比例多路閥的前向通道中，同時將AMESim中建立的比例多路閥結構化模型導入到Simulink中，建立AMESim/Simulink聯合仿真模型,如圖13所示。

圖12 修正黏性摩擦LuGre模型狀態觀測器Fig.12 State observer of the modified viscous friction LuGre model

圖13 比例多路閥摩擦補償聯合仿真模型Fig.13 Co-simulation model of friction compensation for the proportional multi-way valve

3.4 摩擦補償仿真分析

比例多路閥在低速或變向運動時，僅采用PID控制器往往難以滿足控制精度。所以針對修正黏性摩擦LuGre模型設計了摩擦狀態觀測器，進而，采用修正黏性摩擦LuGre模型進行摩擦補償，并與PID控制器補償方法進行仿真對比。PID控制器補償結構如圖14所示。

圖14 PID控制的補償結構圖Fig.14 Compensation structure diagram of PID control

常規PID控制進行仿真時，kP=150，kI=271，kD=0.96。AMESim程序中比例多路閥主要結構參數如表2所示。

輸入幅值為±0.0081 m、頻率為2 Hz的方波信號，仿真時間為1 s，仿真采樣時間為0.01 s，負載力為80 kN。修正黏性摩擦LuGre模型的摩擦補償和PID控制兩種方法的位置跟蹤曲線如圖15所示。

表2 比例多路閥主閥參數
Tab.2 Main valve parameters of the multi-way valve

閥芯直徑(mm)20最大限制位移(mm)8.1閥桿直徑(mm)12最小限制位移(mm)-8.1零位移時開度(mm)-1.5外彈簧剛度(N/m)83靜摩擦力(N)65.42零位移時外彈簧力(N)110.4Stribeck速度(mm/s)0.028零位移時空腔長度(mm)0阻尼孔直徑(mm)1.8內彈簧剛度(N/m)5460閥芯質量(kg)0.25零位移時內彈簧力(N)0

圖15 位置跟蹤曲線圖Fig.15 Position tracking curves

通過圖15位置跟蹤曲線可以看出，基于修正黏性摩擦LuGre模型補償與PID控制相比較，修正黏性摩擦LuGre模型能有效地抑制穩態極限環振蕩，縮短響應時間，減小主閥芯位移誤差。說明修正LuGre黏性摩擦模型能較好地補償摩擦對閥位置跟蹤特性的影響。

4 結論

(1)通過多路閥實驗測試平臺所測得的比例多路閥壓力、流量、閥芯位移等數據，計算獲得主閥芯摩擦力、速度數據。基于修正黏性摩擦LuGre模型辨識出摩擦力與速度的關系曲線，相比于LuGre模型，在Stribeck效應速度處擬合效果好，并且能夠擬合出較高速度階段摩擦力隨速度增大其增長趨勢減緩的特性。

(2)設計了基于修正黏性摩擦LuGre模型摩擦補償控制器，運用AMESim和Simulink進行了摩擦補償聯合仿真。通過與PID常規控制策略相比較，基于修正黏性摩擦LuGre模型狀態觀測器的摩擦補償方法能有效地減小摩擦對比例多路閥性能的影響，為比例閥的設計改進及工程應用提供參考。

[1] 向紅標，譚文斌，李醒飛，等．基于LuGre模型的自適應摩擦補償[J]．機械工程學報，2012，48(17)：70-74. XIANG Hongbiao, TAN Wenbin, LI Xingfei, et al. Adaptive Friction Compensation Based on LuGre Model[J]. Journal of Mechanical Engineering, 2012,48(17):70-74.

[2] AMIRANTE R, DISTASO E, TAMBURRANO P. Experimental and Numerical Analysis of Cavitation in Hydraulic Proportional Directional Valves[J]. Energy Conversion and Management, 2014,87：208-219.

[3] SAHA A, WAHI P, WIERCIGROCH M, et al. A Modified LuGre Friction Model for an Accurate Prediction of Friction Force in the Pure Sliding Regime[J/OL]. International Journal of Non-linear Mechanics. [2015-12-28]. http:// dx.doi.org/10.1016/j.ijnonlinmec.2015.08.013.

[4] 丁千，翟紅梅．機械系統摩擦動力學研究進展[J]．力學進展，2013，43(1)：112-131. DING Qian, ZHAI Hongmei. The Advance in Researches of Friction Dynamics in Mechanics System[J]. Advances in Mechanics,2013,43(1):112-131.

[5] KHAYATI K, BIGRAS P, DESSAINT L A. LuGre Model-based Friction Compensation and Positioning Control for a Pneumatic Actuator Using Multi-objective Output-feedback Control via LMI Optimization[J]. Mechatronics,2009,19(4):535-547.

[6] NASER M F M, IKHOUANE F. Hysteresis Loop of the LuGre Model[J]. Automatica,2015,59:48-53.

[7] 郭彥青，付永領，張朋．一種新型LuGre摩擦模型參數辨識方法[J]．機床與液壓，2015，43(1)：150-152. GUO Yanqing, FU Yongling, ZHANG Peng. A Novel Parameters Identification Method for LuGre Friction Model[J]. Machine Tool & Hydraulics,2015,43(1):150-152.

[8] RUDERMAN M. Presliding Hysteresis Damping of LuGre and Maxwell-slip Friction Models[J]. Mechatronics,2015,30:225-230.

[9] 劉柏希，劉宏昭．基于LuGre摩擦模型的有桿抽油系統動態特性分析[J]．中國機械工程，2009，20(18)：2236-2240. LIU Baixi, LIU Hongzhao. Analysis for Dynamic Characteristics of the Suckerrod Pumping System Based on LuGre Friction Model[J]. China Mechanical Engineering,2009,20(18):2236-2240.

[10] 周金柱，段寶巖，黃進．LuGre摩擦模型對伺服系統的影響與補償[J]．控制理論與應用，2009，25(6)：990-994. ZHOU Jinzhu, DUAN Baoyan, HUANG Jin. Effect and Compensation for Servo Systems Using LuGre Friction Model[J]. Control Theory & Applications,2009,25(6):990-994.

[11] 劉柏希，姚昊雄，聶松輝．基于區間分析的LuGre摩擦模型參數辨識方法[J]．中國機械工程，2013，24(19)：2647-2651. LIU Baixi, YAO Haoxiong, NIE Songhui. Parameter Identification of LuGre Frition Model Based on Interval Analysis[J]. China Mechanical Enginee-ring,2013,24(19):2647-2651.

[12] 王瑞娟，梅志千，李向國，等．機電伺服系統非線性摩擦自適應補償的研究[J]．中國電機工程學報，2012，32(36)：124-129. WANG Ruijuan, MEI Zhiqian, LI Xiangguo, et al. Research on Adaptive Nonlinear Friction Compensation of Mechatronic Servo Systems[J]. Proceedings of the CSEE,2012,32(36):124-129.

[13] 譚文斌，李醒飛，向紅標，等．修正黏性摩擦的LuGre模型的摩擦補償[J]．天津大學學報，2012，45(9)：825-828. TAN Wenbin, LI Xingfei, XIANG Hongbiao, et al. Friction Compensation Based on LuGre Model with Modified Viscous Friction[J]. Journal of Tianjin University,2012,45(9):825-828.

[14] PIATKOWSKI T. Dahl and LuGre Dynamic Friction Models—The Analysis of Selected Properties[J]. Mechanism and Machine Theory,2014,73(2):91-100.

[15] 張劍. 含摩擦伺服系統的建模與控制研究[D]．合肥：中國科學技術大學，2011. ZHANG Jian. Modeling and Control of Servo System with Friction[D]. Hefei: University of Science and Technology of China, 2011.

[16] ZHANG Z, LI Z, ZHOU Q, et al. Application in Prestiction Friction Compensation for Angular Velocity Loop of Inertially Stabilized Platforms[J]. Chinese Journal of Aeronautics,2014,27(3):655-662.

(編輯 袁興玲)

Friction Compensation of Proportional Multi-way Valve Based on Modified Viscous Friction LuGre Model

CHEN Dongning1,2LIU Yidan1,2YAO Chengyu3JIANG Donglin1,2WANG Kexun1,2

1.Hebei Provincial Key Laboratory of Heavy Machinery Fluid Power Transmission and Control,Yanshan University, Qinhuangdao, Hebei, 066004 2. Key Laboratory of Advanced Forging & Stamping Technology and Science(Yanshan University),Ministry of Education of China, Qinhuangdao, Hebei, 066004 3. Key Laboratory of Industrial Computer Control Engineering of Hebei Province, Yanshan University,Qinhuangdao, Hebei, 066004

To decrease the influences of friction on the proportional multi-way valves, the methods of friction characteristic analysis, parameter identification and friction compensation of proportional multi-way valves were proposed based on modified viscous friction LuGre model. The friction data were indirectly obtained through the experimental tests. The static and dynamic parameters of modified viscous friction LuGre model were identified by data fitting. The friction state observer of modified viscous friction LuGre model was designed by use of the identified parameters, and the output of state observer was fed back to the input port of control model to reduce the adverse effect of friction on the proportional multi-way valve performances. Simulation results show that the location tracking accuracy of proportional multi-way valves may be improved by using the friction compensation with identification parameter method based on modified viscous friction LuGre model.

proportional multi-way valve; friction compensation; LuGre model; viscous friction; parameter identification

2016-03-21

國家自然科學基金資助項目(51675460，51405426)；河北省自然科學基金資助項目(E2016203306)

TH137.52；TH117.1

10.3969/j.issn.1004-132X.2017.01.011

陳東寧，女，1978年生。燕山大學機械工程學院副教授、電氣工程學院博士后研究人員。主要研究方向為系統可靠性、故障診斷及智能優化。獲國家科技進步二等獎1項。發表論文40余篇。E-mail:dnchen@ysu.edu.cn。劉一丹，女，1992年生。燕山大學機械工程學院碩士研究生。姚成玉，男，1975年生。燕山大學電氣工程學院教授、博士后研究人員。蔣棟林，男，1985年生。燕山大學機械工程學院碩士研究生。王可勛，男，1988年生。燕山大學機械工程學院碩士研究生。