基于傳輸線方程的多根非平行傳輸線串擾分析
劉鑫+鐘選明+葉志紅+廖成

摘 要: 非平行結構的傳輸線在電力電子系統中普遍存在,當其上通有電壓和電流信號時,會在周圍傳輸線上產生串擾響應。采用時域傳輸線方程建立多根非平行傳輸線之間的串擾模型,結合FDTD方法,分析在脈沖集總源激勵下受擾導線始端和終端負載上的串擾電壓響應特性,將其結果與仿真結果對比,驗證了該方法的正確性。研究結果表明,非平行結構中受擾線始端和終端負載上的串擾電壓響應隨著傳輸線離地面高度的增大而增大,隨著傳輸線之間夾角的增大而變小,且減小的趨勢逐漸減弱,從而為線纜間的串擾防護提供了參考依據。
關鍵詞: 非平行傳輸線; 時域傳輸線方程; 串擾響應; FDTD
中圖分類號: TN811?34 文獻標識碼: A 文章編號: 1004?373X(2017)01?0163?04
Abstract: The transmission line with non?parallel structure is prevalent in the power electronic system, and the crosstalk response will be produced around it when the voltage and current signals are transmitted through it. The time?domain transmission line equation is used to establish the crosstalk model among the multiconductor non?parallel transmission lines. The FDTD method is combined to analyze the crosstalk voltage response characteristics of the disturbed conductor beginning and terminal loads under the pulse lumping source excitation. The results are contrasted with the simulation results to verify the validity of the method. The research results show that the crosstalk voltage response of the disturbed conductor beginning and terminal loads in non?parallel structure is increased with the height increasing of the transmission line, decreased with the included angle increasing between the transmission lines, and the decrease trend is decayed gradually, which provides a reference for the crosstalk protection among cables.
Keywords: non?parallel transmission line; time?domain transmission line equation; crosstalk response; FDTD
0 引 言
在電氣設備、電子儀器中,由于內部連接傳輸線較多,線與線之間常常是密集且以非平行結構分布排列的,這樣就導致導線之間容易產生串擾現象,從而使設備遭受影響,導致性能降低或功能不正常。文獻[1]指出傳輸線間的串擾是電器工程中常見的電磁干擾模式。因此在電磁兼容問題上,對傳輸線間的串擾問題進行研究顯得尤為重要。
當非平行傳輸線上通有電壓和電流信號時,會在其周圍產生電磁場,從而在其他傳輸線上產生串擾響應,影響傳輸線兩端設備的正常工作。國內外在傳輸線串擾問題的計算方法和特性分析上也做了一定研究。文獻[2?6]對多導體傳輸線在時域和頻域上的串擾分析做了大量研究,例如文獻[7]分析了單導體傳輸線與屏蔽電纜的串擾問題,文獻[8]則基于BLT(Baum?Liu?Tesche)方程對線纜網絡的電磁干擾響應進行求解,但其分析和計算的對象都是平行結構的傳輸線,對于非平行結構的傳輸線則沒有涉及。而文獻[9]中則采用頻域BLT方程,離散傳輸線并引入理想節點的概念計算非平行傳輸線間的串擾響應,文獻[10]采用階梯式均勻傳輸線模型,對非平行傳輸線進行分段逼近,文獻[11]利用基于Daubechies小波函數的MRTD方法計算非平行微帶線間的夾角對串擾的影響。
目前對非平行結構的傳輸線研究,文獻中多采用基于BLT方程的頻域算法分析傳輸線的串擾問題,但頻域BLT方程涉及大量矩陣運算,且計算相對復雜。本文將時域傳輸線方程和FDTD方法結合起來,采用傳輸線方程建立非平行導體的串擾模型,利用FDTD的差分格式對傳輸線方程進行離散,計算在集總激勵源下的受擾線始端和終端負載的時域串擾電壓,同時分析了非平行傳輸線結構的串擾特性。
1 傳輸線模型
結合傳輸線方程將非平行傳輸線進行離散,把每一個離散線段近似地看作是平行結構,從而求得非平行結構傳輸線的串擾電壓響應。
1.1 非平行傳輸線模型
考慮如圖1(a)所示的情況,為平行于地面且相互不平行的兩條傳輸線,分別為離地面的高度,和分別為兩傳輸線之間的距離和夾角,傳輸線的始端接有激勵源其內阻為終端接負載傳輸線的兩端分別接有負載和為干擾線,為受擾線。
把傳輸線離散成段,每段按照平行的結構進行分析處理,計算出每段的分布參數,最后根據傳輸線方程的差分格式求得非平行傳輸線的串擾電壓響應。
2 計算結果
通過使用商業仿真軟件對非平行結構傳輸線的算例進行模擬,驗證了本文提出方法的正確性,并在此基礎上分析了非平行傳輸線之間以及離地高度對串擾電壓的影響。
2.1 算法正確性驗證
如圖1(a)所示,選取半徑0.001 m,夾角為5°的非平行傳輸線0.15 m,0.150 57 m且與參考坐標平行,離地高度均為0.01 m,0.01 m, Ω, Ω。采用雙指數脈沖作為激勵源,如圖3所示。
非平行傳輸線在雙指數脈沖激勵下,受擾線近端和遠端的電壓響應曲線如圖4所示。其中虛線表示使用FDTD程序計算的結果,實線表示在同一計算模型下,使用商業軟件仿真的結果。從圖中可以看出兩種方法的計算結果基本吻合,從而驗證了本文非平行傳輸線串擾計算方法的正確性。
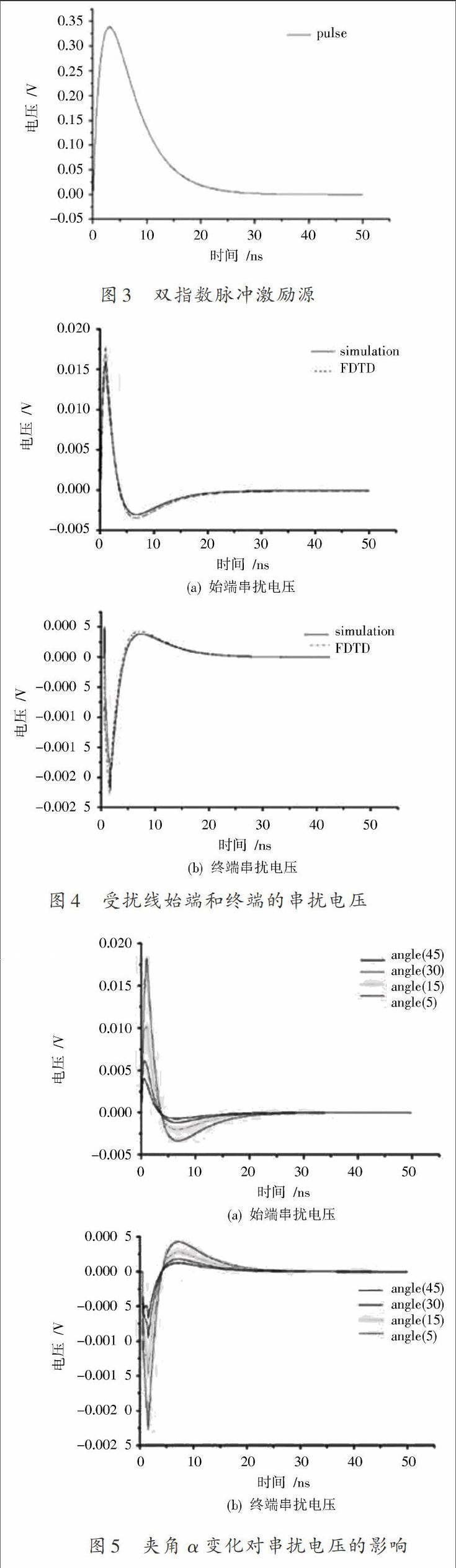
2.2 夾角對非平行傳輸線串擾特性的影響
如圖5所示,干擾線和受擾線參數不變,且處于同一平面內,分別計算非平行雙線夾角為5°,15°,30°和45°四種情況下受擾線始端和終端的串擾電壓。從圖5中可以看出: =15°時比=5°時串擾電壓減少約7 mV,=30°時比=15°時串擾電壓減少約3.5 mV,=45°時比=30°時串擾電壓減少2 mV。隨著夾角角度的增加,線間串擾電壓呈現明顯的減小趨勢,但減小的趨勢逐漸減弱。這是因為當夾角增大時,受擾線與干擾線之間的整體距離是增加的,傳輸線之間的耦合減小,這也說明傳輸線間的夾角對電磁干擾的影響很大。
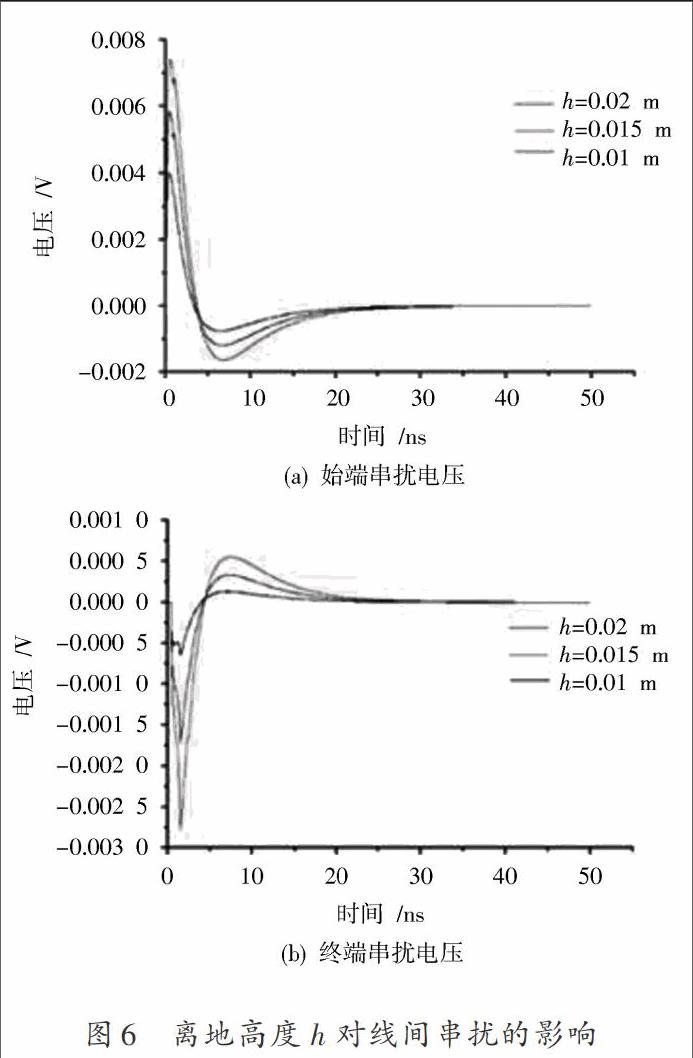
2.3 離地高度對非平行傳輸線串擾特性的影響
如圖6所示,在干擾線和受擾線參數不變,兩傳輸線間夾角為45°的情況下,傳輸線距離地面的高度分別為0.01 m,0.015 m,0.02 m,求得受擾線始端和終端的串擾電壓,由圖6可知,傳輸線距離地面越高,始端和終端的串擾電壓越大,這是由于隨著高度的增大,使得傳輸線上每一離散段的自電感和互電感增加所造成的。
3 結 語
本文采用時域傳輸線方程建立了非平行傳輸線的串擾模型,采用FDTD的差分格式對傳輸線方程進行離散,得到了在脈沖集總激勵源下受擾線始端和終端負載上的串擾電壓響應。通過商業仿真軟件對非平行傳輸線串擾模型的數值模擬,驗證了本文提出算法的正確性,同時,分析了非平行傳輸線的串擾特性。結果表明兩線間夾角越大,串擾電壓越小,且減小的趨勢逐漸減弱;兩線離地高度越高,串擾電壓越大。為研究復雜電磁環境下的電子系統電磁干擾問題提供了一定的理論依據。
參考文獻
[1] 葉烽,黨松.電磁兼容性技術的內涵及其發展[J].現代電子技術,2001,24(1):65?69.
[2] OMID M, KAMI Y, HAYAKAWA M. Field coupling to non?uniform and uniform transmission lines [J]. IEEE transactions on EMC, 1997, 39(3): 201?211.
[3] PAUL C R. Analysis of multiconductor transmission lines [M]. New York: Wiley, 1994: 223?312.
[4] CELOZZI S, FELIZIANI M. Time?domain solution of field excited multiconductor transmission line equations [J]. IEEE transactions on EMC, 1995, 37(3): 421?431.
[5] PAUL C R. Literal solutions for the time?domain response of a two?conductor transmission line excited by an incident electromagnetic field [J]. IEEE transactions on EMC, 1995, 37(2): 241?251.
[6] 張志軍.電磁脈沖對傳輸線耦合規律的研究[D].北京:華北電力大學,2006.
[7] 周大瑜,廖成,葉志紅,等.屏蔽腔體中多導體傳輸線串擾抑制的仿真研究[J].現代電子技術,2015,38(8):148?150.
[8] 高雪蓮,張曉宇,趙磊,等.基于BLT方程的復雜線纜網絡電磁干擾響應求解[J].科學技術與工程,2015(5):248?252.
[9] 覃宇建,周東明,何建國.BLT方程在任意布局傳輸線串擾分析中的應用[J].國防科技大學學報,2009,31(2):55?58.
[10] 張友文,劉光斌.非均勻傳輸線間的串擾研究[J].微波學報,2011(4):85?87.
[11] 權赫,孫兆牛.抑制非平行微帶線間串擾的保護帶方法研究[J].電子測量與儀器學報,2011(10):850?856.

