彈殼體結(jié)構(gòu)對燃料裝藥拋撒速率影響的數(shù)值模擬研究
王曄,白春華,李建平
(北京理工大學 爆炸科學與技術(shù)國家重點實驗室,北京 100081)
彈殼體結(jié)構(gòu)對燃料裝藥拋撒速率影響的數(shù)值模擬研究
王曄,白春華,李建平
(北京理工大學 爆炸科學與技術(shù)國家重點實驗室,北京 100081)
為研究殼體結(jié)構(gòu)對燃料近區(qū)拋撒速率的影響,利用LS-DYNA程序,分別對無加強桿結(jié)構(gòu)和有加強桿結(jié)構(gòu)的中心拋撒藥驅(qū)動燃料拋撒和殼體破壞過程進行數(shù)值模擬,并與試驗結(jié)果進行了對比,得到了燃料邊界初始膨脹狀態(tài)、殼體破裂過程和刻槽應(yīng)力隨時間變化的規(guī)律,以及不同結(jié)構(gòu)對燃料拋撒最大速率的影響。研究結(jié)果表明:在滿足結(jié)構(gòu)強度的要求且徑向強度相同的情況下,加強殼體的軸向拉力,能夠有效提高燃料拋撒速率;在相同的中心藥量/燃料量的情況下進行拋撒,當軸向拉力提高0.7×106N時,有加強桿結(jié)構(gòu)較無加強桿結(jié)構(gòu)有利于獲得較大的拋撒速率,有加強桿結(jié)構(gòu)的燃料最大拋撒速率可達316.3 m/s,無加強桿結(jié)構(gòu)的燃料最大拋撒速率為285.3 m/s,燃料拋撒最大速率提高了10.8%.
兵器科學與技術(shù);有加強桿結(jié)構(gòu);無加強桿結(jié)構(gòu);拋撒速率;數(shù)值模擬
0 引言
在驅(qū)動載荷作用下的燃料拋撒技術(shù)[1-4],目前廣泛應(yīng)用于消防、煤礦、化工、煙花爆竹和軍事等領(lǐng)域,如滅火彈、爆破除塵和燃料空氣炸藥、煙花燃放等。為了在不同場合應(yīng)用,通常需要將被拋撒物質(zhì)置于固定的容器中,便于儲存、運輸和使用。為此世界各國學者開展了燃料空氣混合物形成過程的相關(guān)研究。
被拋撒物作為最終的考察和分析對象,無論是研究爆轟驅(qū)動平板飛片的運動特性試驗[5-7]和數(shù)值計算[8-11],或是探討球形金屬顆粒拋撒規(guī)律的最初階段,均需要考慮并設(shè)計合理的殼體(容器)結(jié)構(gòu)[12]。從起爆到殼體膨脹、破裂為破片的過程,以及燃料拋撒、破碎、霧化的過程,是爆轟驅(qū)動燃料拋撒的兩個外在表現(xiàn)形式。相同中心藥/燃料量的裝藥結(jié)構(gòu),在形成扁平狀的云霧形態(tài)時,可以達到最強的破壞效應(yīng)[13]。另有研究者研究發(fā)現(xiàn),覆蓋范圍越廣且貼在地面上的扁平狀云霧點爆后,其破壞效應(yīng)較強[14],因此學者們[15-22]利用實驗室等效試驗和數(shù)值模擬技術(shù),對控制燃料拋撒形成扁平狀云霧的技術(shù)開展了一系列的研究。研究結(jié)果表明,殼體的破裂過程直接影響到燃料的分散狀態(tài),因此只有合理的殼體結(jié)構(gòu)才能達到預期目的。其中殼體軸向約束拉力的改變,對燃料拋撒速率的影響較為關(guān)鍵。
本研究針對無加強桿結(jié)構(gòu)和有加強桿結(jié)構(gòu),在中心拋撒藥驅(qū)動下,對燃料的拋撒初始速率和殼體破壞的過程進行數(shù)值模擬,并在試驗結(jié)果對比的基礎(chǔ)上,分析了兩種結(jié)構(gòu)對燃料拋撒的影響規(guī)律。
1 結(jié)構(gòu)模型
有無加強桿結(jié)構(gòu)和有加強桿結(jié)構(gòu)兩種殼體結(jié)構(gòu)。無加強桿結(jié)構(gòu)由中心管、上下加強端板以及筒壁組成,而有加強桿結(jié)構(gòu)在無加強桿結(jié)構(gòu)的基礎(chǔ)上,增加加強桿,對稱分布在筒壁內(nèi)部。在筒壁上均勻分布深度為0.6 mm的16道刻槽;上下端板為圓形截面,直徑為370 mm;筒壁為長度1 150 mm的柱形。內(nèi)部裝填125 kg混合燃料,中心管內(nèi)部裝填1.08 kg TNT,作為中心拋撒藥。結(jié)構(gòu)與尺寸如圖1所示。

圖1 兩種結(jié)構(gòu)模型尺寸Fig.1 Geometric models
2 模擬參數(shù)
2.1 計算模型

圖2 無加強桿結(jié)構(gòu)和有加強桿結(jié)構(gòu)的計算模型Fig.2 Computation models for different structures
按照圖1所示尺寸,進行1∶1建模。空氣區(qū)域尺寸為1 m×1 m×2 m,兩種結(jié)構(gòu)的計算模型如圖2所示。
2.2 計算方法
計算方法采用流體- 固體耦合算法,單元采用單點積分的ALE多物質(zhì)單元,研究殼體破裂情況以及燃料拋撒狀態(tài)。中心拋撒藥、燃料和空氣區(qū)域采用Euler網(wǎng)格,殼體各結(jié)構(gòu)采用Lagrange網(wǎng)格。由于兩種結(jié)構(gòu)為軸對稱結(jié)構(gòu),為了節(jié)省運算時間,采用1/4模型進行計算分析。
2.3 材料參數(shù)
2.3.1 中心拋撒藥
利用MAT_HIGH_EXPLOSIVE_BURN材料模型和選用JWL狀態(tài)方程進行描述中心拋撒藥,拋撒藥
選用TNT,主要材料計算參數(shù)如表1[9]所示。JWL狀態(tài)方程形式為
(1)
式中:p為爆轟產(chǎn)物的壓力;V是相對比體積;e是單位體積炸藥的內(nèi)能;A、B、R1、R2、ω均為JWL狀態(tài)方程參數(shù)。
2.3.2 燃料
為便于分析,混合燃料用水代替。燃料模型采用MAT_NULL材料模型和Gruneisen狀態(tài)方程進行描述,主要參數(shù)見表2所示。Gruneisen狀態(tài)方程形式為

表1 拋撒藥的主要計算參數(shù)Tab.1 Computation parameters of central high-explosive
注:ρ為質(zhì)量密度,D為爆轟速度。
(2)
式中:C是沖擊波傳播速度;γ0是Gruneisen指數(shù);α是γ0的一階體積修正量;μ=(ρ/ρ0)-1,ρ0為燃料初始質(zhì)量密度;S1、S2、S3為Gruneisen狀態(tài)方程的系數(shù)。

表2 燃料的基本計算參數(shù)Tab.2 Parameters of fuel
2.3.3 空氣
空氣采用MAT_NULL材料模型和線性多項式LINEAR_POLYNOMIAL狀態(tài)方程,主要計算參數(shù)如表3所示。狀態(tài)方程表達形式為
p=c0+c1μ+c2μ2+c3μ3+
(c4+c5μ+c6μ2)e,
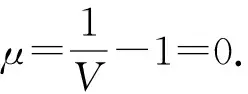
2.3.4 結(jié)構(gòu)材料
殼體結(jié)構(gòu)選用PLASTIC_KINEMATIC材料模型,該模型可較為準確地模擬殼體在爆炸過程中發(fā)生的彈性變形、塑性變形以及破裂等過程。各結(jié)構(gòu)主要材料參數(shù)如表4所示。

表3 空氣的基本計算參數(shù)Tab.3 Computation parameters of air

表4 殼體的計算參數(shù)Tab.4 Parameters of components
注:E為彈性模量,υ為泊松比,σs為屈服應(yīng)力,Et為屈服段模量,δ為失效應(yīng)變量。
2.3.5 初始條件和邊界條件
初始條件:為了更真實地模擬該裝置的初始作用過程,采用一端起爆,即下端中心起爆方式。
邊界條件:由于殼體外部為無限邊界的空氣,故邊界條件采用無反射邊界條件。
2.3.6 網(wǎng)格的選取和計算時長
終止計算條件由計算時間決定,計算時間為2 ms,當拋撒時間到達2 ms時停止計算。每隔10 mm對1/4模型進行映射網(wǎng)格劃分,體單元形狀為六面體。模型總計算時長約為15 h.
3 模擬結(jié)果分析討論
3.1 殼體破裂過程
由于殼體破裂的先后順序,直接影響燃料拋撒的形態(tài)變化,因此殼體破裂過程的結(jié)果如圖3所示。從圖3中觀察到:在0~1 ms之間時,兩種結(jié)構(gòu)由于中心藥爆轟作用,筒壁由下向上進行膨脹,刻槽由于強度較弱首先破裂失效,導致筒壁開裂,兩種結(jié)構(gòu)筒壁均形成條狀破片;當在1~2 ms之間時,筒壁破片與上下端板脫離,向四周運動,此時,無加強桿結(jié)構(gòu)的部件均已失效,而有加強桿結(jié)構(gòu)上下端板之間的約束依然存在。顯然,產(chǎn)生這種區(qū)別的原因是有加強桿結(jié)構(gòu)具有加強桿,使得整個結(jié)構(gòu)的抗軸向拉力能力增強,導致爆轟作用力集中在徑向,使得筒壁快速破裂,導致有桿加強結(jié)構(gòu)的筒壁破裂較無加強桿結(jié)構(gòu)筒壁破裂更徹底。

圖3 殼體應(yīng)力的數(shù)值模擬結(jié)果Fig.3 Simulated results of shell stress
3.2 刻槽單元應(yīng)力分析
已有研究[9]表明軸向中部橫截面的燃料拋撒效果最為顯著,且具有對稱性,因此選擇中部橫截面為觀察面,即選擇距離下端板底端525 mm處的刻槽單元為監(jiān)測點,刻槽單元應(yīng)力隨時間變化的結(jié)果如圖4所示。從圖4中可以看出:兩種結(jié)構(gòu)的應(yīng)力變化趨勢相同,均表現(xiàn)為隨時間單調(diào)增加;隨著時間的增加,刻槽應(yīng)力達到最大值時,爆轟波峰值超壓超過刻槽破裂臨界應(yīng)力后,刻槽破裂,應(yīng)力迅速減小至0 GPa,此時,看作燃料開始拋撒。

圖4 殼體刻槽位置單元的應(yīng)力時程曲線Fig.4 Stress of cutting cells versus time
根據(jù)牛頓第三定律,隨著驅(qū)動力的不斷增加,刻槽約束應(yīng)力也在不斷增加,最終達到殼體刻槽破裂應(yīng)變量臨界值,導致殼體約束應(yīng)力失效。從圖4 可以看出,有加強桿結(jié)構(gòu)失效時間為0.44 ms,而無加強桿結(jié)構(gòu)失效時間為0.49 ms. 其原因是:在相同的驅(qū)動力作用下,強度較弱的地方先破裂。在無加強桿結(jié)構(gòu)中,其軸向拉力小于有加強桿結(jié)構(gòu)的軸向拉力;在有加強桿結(jié)構(gòu)中,加強桿部件增大了軸向約束力,使得徑向拉力弱于軸向拉力,在筒壁結(jié)構(gòu)相同的情況下,使得驅(qū)動力的作用力集中在徑向筒壁的拉伸,因此導致有加強桿結(jié)構(gòu)的刻槽應(yīng)力失效時間早于無加強桿結(jié)構(gòu)的刻槽應(yīng)力失效時間。
3.3 燃料水平拋撒速率
兩種結(jié)構(gòu)均為圓柱筒壁,所以在徑向方向的約束力相等,而軸向方向約束力由于部件的差異導致不同。在進行軸向約束計算時,兩種結(jié)構(gòu)的差異在加強桿部件,因此兩種結(jié)構(gòu)的約束力差值就是加強桿部件的約束力,約束力[23]差值為
W=d2σa/2,
(4)
式中:W為約束力;d為加強桿截面直徑,d=0.018 m;σa為屈服強度,由于加強桿部件材料為30CrMnSiA圓鋼材料,則σa=1 080 MPa.
根據(jù)(4)式,則軸向約束力差值ΔW=4W=0.7×106N. 可見,兩種裝置結(jié)構(gòu)強度只在軸向方向上相差0.7×106N.

圖6 有加強桿結(jié)構(gòu)燃料拋撒試驗的結(jié)果Fig.6 Experiment results of fuel dispersion for stiffener structures
選擇中部橫截面為觀察面,即選擇距離下端板底端525 mm處的燃料拋撒單元為監(jiān)測點,不同結(jié)構(gòu)燃料中部橫截面拋撒速率隨時間變化的結(jié)果如圖5所示。由圖5可知,兩種結(jié)構(gòu)在燃料速率呈現(xiàn)相似的變化規(guī)律,變化主要為先快速上升,后下降、振蕩,再逐漸上升的趨勢。在中心拋撒藥爆轟作用下,燃料由靜止狀態(tài)開始加速,拋撒速率快速上升;殼體受到應(yīng)力波沖擊并破裂,燃料噴射到空氣中,受到空氣阻力作用,燃料速率進入減速階段;隨著中心拋撒藥產(chǎn)生的爆轟產(chǎn)物向外擴散推動燃料,燃料速率又有所上升。有加強桿結(jié)構(gòu)的燃料拋撒速率大于無加強桿結(jié)構(gòu)。有加強桿結(jié)構(gòu)的燃料最大拋撒速率可達316.3 m/s,而無加強桿結(jié)構(gòu)的燃料最大拋撒速率為285.3 m/s,二者相差31.0 m/s,燃料拋撒最大速率提高了10.8%. 這是由于有加強桿結(jié)構(gòu)的軸向約束力大于無加強桿結(jié)構(gòu),使得徑向刻槽應(yīng)力失效時間早于無加強桿結(jié)構(gòu)的刻槽應(yīng)力失效時間,阻力時間作用較短,使得燃料加速充分,獲得較大的初始速率。

圖5 不同結(jié)構(gòu)燃料拋撒速率的時程曲線Fig.5 Initial dispersing velocities of two types of shells versus time
3.4 模擬與試驗驗證
為了驗證模擬結(jié)果,進行燃料拋撒試驗。試驗中采用有加強桿殼體結(jié)構(gòu)(見圖1(b))。將殼體垂直擺放在試驗架上,下端板距離地面高度為1.5 m. 擺放位置作為爆心,以爆心作為原點,距離爆心為15 m處布置兩對標志桿,用來讀取燃料拋撒半徑,進而得到拋撒速率。高速攝影儀垂直于標志桿布置,型號為V12,分辨率為1 280×800,拍攝速度為2 000幀/s.
圖6為試驗記錄到的燃料拋撒過程。由起爆后記錄的時刻云霧形狀看,結(jié)構(gòu)變形及破裂情況模擬結(jié)果與實際相一致。
將燃料拋撒初始速率與試驗結(jié)果進行對比,如表5所示。雖然燃料拋撒初始拋撒速率的數(shù)值模擬結(jié)果和試驗結(jié)果之間存在誤差,但是計算值與試驗結(jié)果在燃料拋撒前期的總體趨勢一致,顯然到2 ms時速率誤差較大。因此,需要將總計算時間控制在殼體破壞前的2 ms時間內(nèi),模擬結(jié)果與試驗結(jié)果較為相符。

表5 燃料拋撒初始拋撒速率的計算結(jié)果與試驗值對比Tab.5 Calculated and experimental results at the same time
燃料拋撒初始速率的數(shù)值模擬和試驗結(jié)果之間存在誤差是由于以下3點造成的:1)計算中采用水的狀態(tài)模型代替了試驗中使用的燃料,因此導致二者在殼體破裂的均勻性方面略有差異;2)在運用有限元分析方法來進行計算時,方法本身存在計算誤差;3)試驗裝置本身存在的工藝誤差,以及記錄設(shè)備的精度和記錄的同步誤差。
4 結(jié)論
本文基于中心拋撒藥、燃料以及殼體結(jié)構(gòu)的數(shù)值模擬仿真模型,對有加強桿結(jié)構(gòu)和無加強桿結(jié)構(gòu)的殼體進行數(shù)值研究,得到如下結(jié)論:
1)有加強桿結(jié)構(gòu)較無加強桿結(jié)構(gòu)有利于獲得較大的拋撒速率,有加強桿結(jié)構(gòu)的燃料最大拋撒速率可達316.3 m/s,而無加強桿結(jié)構(gòu)的燃料最大拋撒速率為285.3 m/s.
2)有加強桿結(jié)構(gòu)較無加強桿結(jié)構(gòu)具有較強的軸向拉力,在相同的中心藥量/燃料量的情況下進行拋撒,當軸向拉力提高0.7×106N時,燃料拋撒最大速率提高了10.8%.
采用數(shù)值模擬仿真模型對燃料邊界初始膨脹狀態(tài)、殼體破裂情況以及最大拋撒速率進行模擬分析,模擬結(jié)果與試驗燃料拋撒初期形狀吻合較好,可為殼體結(jié)構(gòu)的設(shè)計提供參考依據(jù)。
References)
[1] 國家煤礦安全監(jiān)察局事故查詢系統(tǒng)[DB/OL]. http:∥media.chinasafety.gov.cn:8090/isystem/shigumain.jsp. Accident inquiry system of national coal mine safety supervision bureau[DB/OL]. http:∥media.chinasafety.gov.cn:8090/isystem/shigumain.jsp.(in Chinese)
[2] 張國順. 中國兵器工業(yè)安全生產(chǎn)50年[J].兵工安全技術(shù), 2000(2): 5-9. ZHANG Guo-shun. The safe production of China’s weapons industry in 50 years[J]. Ordnance Safety Technology, 2000(2):5-9. (in Chinese)
[3] 王瑩, 馬富學. 新概念武器原理[M]. 北京:兵器工業(yè)出版社, 1997:485-488. WANG Ying, MA Fu-xue. The theory of new concept weapon[M]. Beijing: Publishing House of Ordnance Industry, 1997:485-488. (in Chinese)
[4] Rao A A. Fuel air explosives[J]. Defence Science Journal, 1987, 37(1):23-28.
[5] Liu G, Hou F, Cao B, et al. Experimental study of fuel-air explosive[J]. Combustion, Explosion and Shock Waves, 2008, 44(2): 213-217.
[6] Zhang Q, Bai C H, Dang H Y, et al. Critical ignition temperature of fuel-air explosive[J]. Defence Science Journal, 2004, 54(4):469-474.
[7] Apparaoa A, Rao C R, Tewari S P. Studies on formation of unconfined detonable vapor cloud using explosive means[J]. Journal of Hazard Material, 2013, 254/255:214-220.
[8] Qi Z, Kezhen W, Aimin L, et al. Numerical simulation on dispersal character of fuel by central HE[J]. Defence Science Journal, 2007, 57(4):425-433.
[9] 陳明生, 白春華, 李建平. 燃料拋撒的初始速率與結(jié)構(gòu)動態(tài)響應(yīng)數(shù)值模擬[J].含能材料, 2015, 23(4):323-329. CHEN Ming-sheng, BAI Chun-hua, LI Jian-ping. Simulation on initial velocity and structure dynamic response for fuel dispersion[J]. Chinese Journal of Energetic Materials, 2015, 23(4):323-329.(in Chinese)
[10] 李建平, 白春華, 郭昭平. 云爆裝置初始作用過程數(shù)值模擬[J]. 彈箭與制導學報, 2009, 29(5):123-125. LI Jian-ping, BAI Chun-hua, GUO Zhao-ping. Numerical simulation of the initial interaction process of FAE device[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2009, 29(5):123-125.(in Chinese)
[11] 王飛, 白春華, 閆華. 殼體厚度對大口徑FAE戰(zhàn)斗部效應(yīng)仿真研究[J]. 彈箭與制導學報, 2003, 23(3):110-112. WANG Fei, BAI Chun-hua, YAN Hua. The study for the effect of the thickness of cylindrical shell on the fuel dispersing in the FAE warhead design by simulation[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2003, 23(3):110-112.(in Chinese)
[12] Liu Q M, Bai C H. Research on the explosion temperature response of fuel air explosive measured by colorimetric pyrometer[J]. Journal of China Ordnance, 2010, 6(1):59-64.
[13] Leyer J C. An experimental study of pressure fields by exploding cylindrical clouds[J]. Combustion & Flame, 1982, 48(3):251-263.
[14] Fishburn B, Slagg N, Lu P. Blast effect from a pancake shaped fuel drop-air cloud detonation(theory and experiment)[J]. Journal Hazard Material, 1981, 5(1/2):65-75.
[15] 李斌, 解立峰, 韓志偉, 等.激波驅(qū)動下固體顆粒拋撒的實驗研究[J]. 實驗力學, 2012, 27(6):715-720. LI Bin, XIE Li-feng, HAN Zhi-wei, et al. Experimental study of solid particles dispersal induced by shock wave[J]. Journal of Experimental Mechanics, 2012, 27(6):715-720.(in Chinese)
[16] 閆華, 張奇, 白春華. 發(fā)射過載條件下燃料應(yīng)力狀態(tài)的數(shù)值計算[J]. 兵工學報, 2005, 26(5): 609-614. YAN Hua, ZHANG Qi, BAI Chun-hua. Numerical simulation for stress in fuel under launching over loading[J]. Acta Armamentarii, 2005, 26(5):609-614.(in Chinese)
[17] 丁玨, 劉家驄. 液體燃料爆炸拋撒和FAE 形成過程的數(shù)值模擬[J]. 南京理工大學學報, 2000, 24(2):168-171. DING Jue, LIU Jia-cong. Numerical simulation on the process ofexplosive dispersal for forming FAE cloud[J]. Journal of Nanjing University of Science and Technology, 2000, 24(2):168-171.(in Chinese)
[18] 李斌, 解立峰, 倪歐琪, 等. 燃料液滴云霧爆轟特性研究[J]. 彈道學報, 2010, 22(2):90-93. LI Bin, XIE Li-feng, NI Ou-qi, et al. Study on detonation characteristics of fuel drops cloud[J]. Journal of Ballistics, 2010, 22(2):90-93.(in Chinese)
[19] 沈曉波, 魯長波, 李斌, 等, 液體燃料云霧爆轟參數(shù)實驗[J].爆炸與沖擊, 2012, 32(1):108-112. SHEN Xiao-bo, LU Chang-bo, LI Bin, et al. An experimental study of detonation parameters of liquid fuel drops cloud[J]. Explosion and Shock Waves, 2012, 32(1):108-112.(in Chinese)
[20] 李席, 王伯良, 韓早, 等. 液固復合FAE 云霧狀態(tài)影響因素的試驗研究[J]. 爆破器材, 2013, 42(5): 23 -26. LI Xi, WANG Bo-liang, HAN Zao, et al. Experimental study on influencing factors of the cloud status of liquid-solid fuel air explosive[J]. Explosive Materials, 2013, 42(5):23-26.(in Chinese)
[21] 李斌, 解立峰, 韓志偉, 等.激波作用下水膜變形和霧化實驗研究[J]. 實驗力學, 2011, 26(4):464-470. LI Bin, XIE Li-feng, HAN Zhi-wei,et al. Study on water films induced by shock wave[J]. Journal of Experimental Mechanics, 2011, 26(4):464-470.(in Chinese)
[22] 薛社生, 劉家驄, 秦承森, 等. 燃料爆炸拋撒成霧的實驗與數(shù)值研究[J]. 爆炸與沖擊, 2001, 21(4): 272-276. XUE She-sheng, LIU Jia-cong, QIN Cheng-sen, et al. Experimental and numerical investigation on explosive dispersal and cloud forming[J]. Explosion and Shock Waves, 2001, 21(4):272-276. (in Chinese)
[23] 祝燮權(quán). 實用五金手冊[M]. 上海:上海科學技術(shù)出版社, 2000. ZHU Xie-quan. Practical hardware manual[M]. Shanghai: Shanghai Scientific & Technical Publishers, 2000. (in Chinese)
Influence of shell Structure on Dispersing Velocity of Fuel-air Mixture
WANG Ye,BAI Chun-hua,LI Jian-ping
(State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing 100081, China)
In order to study the dispersal characteristics for different shell structures, the processes of fuel dispersion and shell breakage driven by central explosive are simulated by LS-DYNA code, and the simulated and experimental results are compared. The boundary expansionstate of fuel and the process of shell breakage are obtained. The variation of cutting force with time and the maximum dispersing velocity of different shell structures are analyzed. Results show that the dispersing velocity of fuel could be effectively increased by enhancing the axial tension while satisfying the structural strength and the same radial strength. When axial tension is up to 0.7×106N, the greater dispersing velocity could be produced by stiffener structure. The maximum dispersing velocity of non-stiffener structure is 285.3 m/s. The maximum dispersing velocity of stiffener structure is 316.3 m/s, that could be increased by 10.8% with the same dose for non-stiffener structure.
ordnance science and technology; stiffener structure; non- stiffener structure; dispersal velocity; numerical simulation
2016-03-23
國家部委預先研究項目(9140A05080507)
王曄(1986—),女,博士研究生。E-mail: wangye_0422@126.com
白春華(1959—),男,教授,博士生導師。E-mail:chbai@bit.edu.cn
TJ410.3+3
A
1000-1093(2017)01-0043-07
10.3969/j.issn.1000-1093.2017.01.006

