有限元分析法在幕墻設計中的應用

王寶偉

（沈陽遠大鋁業工程有限公司，遼寧 沈陽 110027）

有限元分析法在幕墻設計中的應用

王寶偉

（沈陽遠大鋁業工程有限公司，遼寧 沈陽 110027）

隨著復雜結構幕墻工程的出現，有限元分析法逐漸被幕墻設計及工程技術人員所采用。有限元分析法是一種數學的計算方法，它的應用領域非常廣泛，可以適用于線性靜力分析、動態分析、熱分析、流場分析等，幕墻的結構力學分析屬于靜力學的研究范圍，所以有限元法可以很好地用于幕墻構件的線性和非線性的靜力分析。而利用有限元軟件如何有效地對玻璃幕墻進行結構分析也成了研究的一個熱點。目前有限元法主要采用的是位移法，以3個位移分量為基本未知數進行研究。

有限元分析法；幕墻設計；靜力分析；位移分量

有限元分析軟件ANSYS主要包括3個部分：前處理模塊，分析計算模塊和后處理模塊，前處理模塊提供了一個強大的實體建模及網格劃分工具，用戶可以方便地構造有限元模型；分析計算模塊包括結構分析，流體動力學的分析等多種分析工具，可模擬多種物理介質場的相互作用；后處理模塊可將計算結果以彩色等值線等圖形、圖表、曲線形式顯示。

1 計算參數

幕墻相對室外地面的最大計算標高為36.0 m，玻璃靠4個駁接爪和對邊的玻璃肋支撐。

如圖1所示，最大夾膠玻璃板塊為1 500 mm×6 000 mm，玻璃配置為12 mm+1.52 PVB+12 mm夾膠鋼化玻璃，玻璃連接方式為4點支撐加對邊簡支支撐形式，計算組合荷載下的強度的驗算。

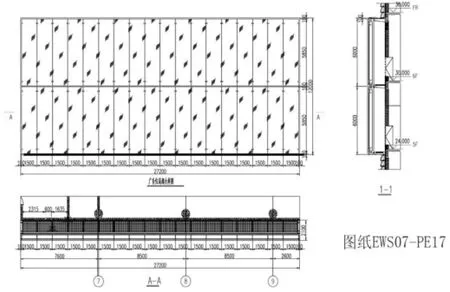
圖1 大樣簡圖

玻璃配置：12 mm+1.52 PVB+12 mm夾膠鋼化玻璃；玻璃短邊長度：La=1 500 mm；玻璃長邊長度：Lb=6 000 mm；外片玻璃板厚：t1=12 mm；內片玻璃板厚：t2=12 mm。

玻璃面板的等效厚度：

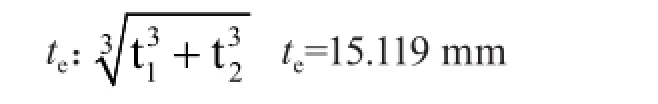
支撐短邊長度：as=La-2×125 mm=1 250 mm

支撐長邊長度：bs=Lb-2×125 mm=5 750 mm

短長邊比值：αp=as/bs=0.217

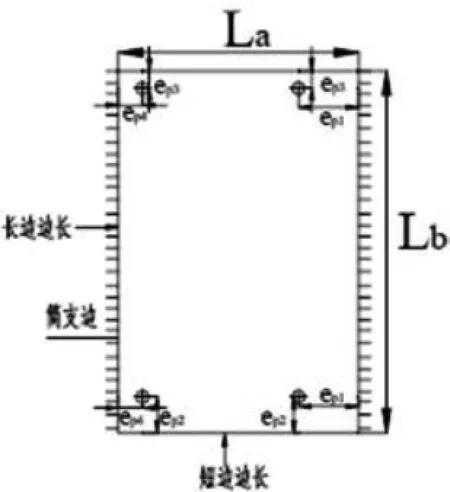
圖2 計算模型

2 荷載標準值的設計計算

2.1 風荷載標準值的設計計算

幕墻相對于室外地坪的最大計算高度：Zh=36m

基本風壓：W0=0.6 kPa 地面粗糙度=“C類”

高度Zh處得陣風系數：βgz=1.868；

風壓高度變化系數見GB50009（2012版）表8.2.1：μz=0.956；

局部風壓體型系數 位置=“負壓墻角” μs（1）=-1.4。

計算玻璃面板時采用的墻面邊最大負壓：

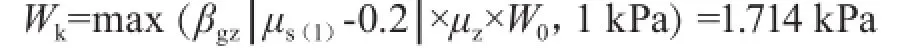
2.2 恒荷載標準值的設計計算

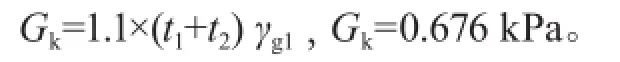
2.3 地震作用的設計計算

地震動力放大系數：βe=5，水平地震影響系數：αmax=0.04

作用在玻璃上的地震作用標準值：

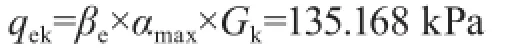
組合荷載下的玻璃強度的驗算：

荷載作用的分項系數及組合系數：

根據外片玻璃和內片玻璃的剛度關系夾膠玻璃分配如下：

2.4 建立模型

有限元模型的創建包括選擇坐標系和單位類型，定義實常數和材料特性，產生實體模型和劃分網格。

點式面玻璃板塊選用shell63板單元模擬，shell63既具有彎曲能力又具有膜力，可以承受平面內荷載和法向荷載。

構件的單元實常數定義如表1所示。

表1 構件的單元實常數定義

采用由點到線，由線及面的順序創建幾何模型，豎框和橫梁的幾何模型簡化為線段，玻璃板塊的幾何模型簡化為由豎框和橫梁各個線段圍成的面域。將幾何模型進行網格劃分，得到點式玻璃幕墻的有限元模型。網格劃分是有限元分析中十分重要的環節網格劃分的粗細程度直接影響到計算時間的長短和計算結果的精確程度。

2.5 約束和加載

對于點式玻璃幕墻起控制作用的是：玻璃面板面內受自重的作用，面外主要受風荷載的作用。荷載按上面計算出的荷載施加，計算強度時，施加外片組合荷載設計值，計算撓度時，施加的是風荷載標準值。

施加位移約束，它的自由度是所有的線位移和點位移的點選。考慮玻璃的自重由駁接爪承擔，并且駁接爪設計吸收了溫度作用引起的平面變形，所以位移的邊界條件約束在圓心位置。由于選用的是4點支撐的力學模型，第1點要求沿Ux，Uy，Uz3個方向約束，第2，3點沿Ux，Uy方向約束，第4點沿Uz方向約束。

2.6 解算及結果分析

在組合荷載作用下，各個節點的變形云圖、應力分布分別如圖3—6所示。

根據有限元計算的結果可知：

玻璃面板的最大應力值σmax=27.5 MPa＜fg1=59 Pa，安全。

玻璃面板的最大位移值νmax=5.1 mm＜La/60=25 mm，安全。

圖3 有限元模型強度計算

圖4 應力云圖

圖5 有限元模型撓度計算

圖6 位移云圖

用簡化算法計算的結果如圖7所示。

工程計算時采用簡化模型計算，采用的是全玻璃的對邊支撐模型，考慮單個桿件在均布荷載作用下的力學性能，選擇強度更高的材料，從而提高了系統的安全系數。

從計算結果上比較，有限元分析法和簡化的結構計算的結果都是可以計算過去的。相對于簡化計算方法，采用有限元法模型中的玻璃板塊構成了有機體系，包括強度和剛度計算，應力和位移分析都是在統一的荷載環境下計算出來的，保持了數據的整體有效性，使玻璃板塊的剛度得到了加強，提高了系統的整體抵抗風荷載的性能。

3 結語

通過兩種計算結果與實驗數據的比較，有限元法整體模型的計算結果更接近于實驗數據，而工程中采用簡化模型計算，使結果更為安全。

由于幕墻機構的結構復雜性，實際分析計算時很難精準地表達出這些邊界條件，而且高層建筑的玻璃幕墻所受荷載與作用也相對復雜，這就使得有限元分析技術目前在幕墻設計中的作用還有很大的局限性，不能更好地發揮其作為數學計算方法的優勢。對有限元數學原理的不斷深化理解，建模計算過程的不斷完善，使其在包括在幕墻的靜力學等領域的應用更為廣泛。

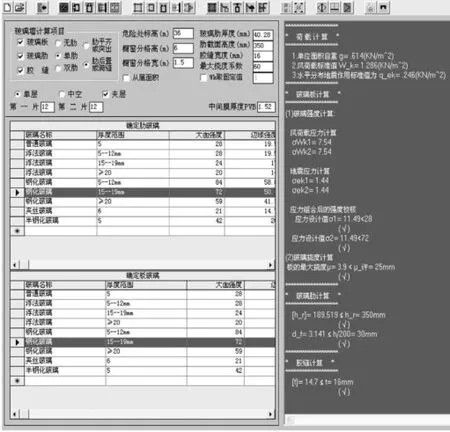
圖7 用簡化算法計算結果

[1]蔣曉豐.淺談利用有限元分析優化檢測機測頭架結構[J].無線互聯科技，2012（5）：66-67.

[2]胡松，孫超鋒，王康康，等.基于ANSYS的壓濾機壓緊板結構優化[J]. 2014（10）：111-112.

Application of fnite element analysis in curtain wall design

Wang Baowei
（Shenyang Broad Aluminum Engineering Co., Ltd., Shenyang 110027, China）

With the advent of curtain wall engineering of complex structure, fnite element analysis method has been designed and used by engineering and technical personnel in curtain wall design. Finite element analysis is a mathematical method, whose application is very extensive, and it can be applied to linear static analysis, dynamic analysis, thermal analysis, fow analysis and so on. Analysis of research scope belongs to the static structural mechanics of curtain wall, so the fnite element method can be used for static analysis of linear and nonlinear components of the curtain wall. How to use the fnite element software to effectively analyze the structure of the glass curtain wall has become a hot research topic. At present, fnite element method is mainly used displacement method, which takes 3 displacement components as basic unknowns.

fnite element analysis method; curtain wall design; static analysis; displacement component

王寶偉（1975—），男，遼寧沈陽，本科，高級工程師；研究方向：幕墻設計。