衛星OFDM系統的同步算法研究

廖為城，朱立東

(電子科技大學 通信抗干擾技術國家級重點實驗室，四川 成都 611731)

衛星OFDM系統的同步算法研究

廖為城，朱立東

(電子科技大學 通信抗干擾技術國家級重點實驗室，四川 成都 611731)

定時偏差和頻率偏移會造成OFDM系統性能嚴重惡化，研究了衛星OFDM系統的同步技術，使OFDM能適應衛星信道低信噪比環境，實現天地一體化通信網絡的融合。在分析了現有的衛星信道條件下OFDM符號定時同步算法和載波頻率同步算法性能的基礎上，根據CAZAC序列相關峰位置受定時偏差和頻率偏移的影響，設計了一種新的訓練序列，并依新訓練序列提出了一種改進的同步算法。仿真結果表明，在衛星信道下該算法在低信噪比時依然具有較高的符號定時同步和載波頻率同步性能，并且在時域信號中就可以實現同步，相比其他在頻域中實現同步的算法減少了復雜度。

OFDM；符號定時同步；載波頻率同步；衛星信道

0 引言

OFDM(正交頻分復用)技術由于其高頻譜利用率、高數據傳輸率等特點被廣泛應用于地面移動通信系統，如LTE系統和WiMAX系統等，因此，研究OFDM技術應用于衛星通信對實現天地一體化通信網絡融合具有重大意義。OFDM技術雖然有諸多優點，但是，由于OFDM各子載波的正交性，導致其對同步的要求較高，因此OFDM在衛星信道下的同步技術是實現OFDM應用于衛星通信的一個關鍵技術。同步技術主要包括符號定時同步和載波頻率同步，OFDM中的頻偏根據對子載波間隔的歸一化，由整數倍頻偏和小數倍頻偏組成。文獻[1]的ML算法利用OFDM的循環前綴進行頻偏估計，但是受多徑影響較大，文獻[2]的Schmidl算法在每個OFDM幀的起始位置使用2個符號作為訓練序列進行同步，但是相關峰有個平臺效應，定時性能差。文獻[3-4]的算法針對Schmidl算法進行了部分改進。文獻[5]根據CAZAC序列的性質提出了較好的同步算法，但是由于訓練序列的特性，使得整數倍頻偏需要為4的整數倍時才可以得到良好的性能。此外，文獻[6-7]針對一些復雜的通信信道研究了OFDM同步技術。

本文在文獻[5]的基礎上，設計了新的訓練序列，根據 CAZAC序列尖銳的自相關峰特性，改進算法在衛星信道低信噪比時也可以實現較好的時偏估計和整數倍頻偏估計。在實現準確定時同步后，可以根據新的訓練序列實現較好的小數倍頻偏估計。

1 OFDM系統模型

基帶OFDM系統工作原理如文獻[8]所示，源信號比特流經過基帶調制映射到QAM星座，再經過串并轉換后進行IFFT變換，使得頻域信號變為時域信號，之后加入循環前綴cp，接著經過并串轉換和數模轉換器，最后經過天線發射OFDM信號。經過物理信道后，接收端經過模數轉換、串并轉換、去除cp、FFT變換、并串轉換和基帶解調等過程得到信宿比特流。

考慮具有N個子載波的OFDM系統，發射端經過IFFT之后的離散復基帶信號可表示為:

(1)

式中，X(k)是第k個子載波上的頻域數據。假設發射信號經過多徑衰落信道的沖激響應為：

(2)

式中,L為多徑數目，hl為第l條路徑的增益，τl為第l條路徑的時延。當系統收發兩端僅存在符號定時偏差和載波頻率偏移時，則經過多徑衰落信道后，接收端第n個抽樣時刻的信號可表示為[5]：

(3)

式中，d為符號定時偏差，ε為以子載波間隔歸一化的載波頻率偏差，可以分為整數倍頻偏εi和小數倍頻偏εf，ω(n)為加性高斯白噪聲。本文所研究的衛星信道通過抽頭延遲線移動信道模型來仿真模擬[9]。

由于定時偏差和頻率偏差會引起OFDM符號間干擾ISI和和載波間干擾ICI[10]，因此必須對它們做估計并進行補償。由于CAZAC序列的相關峰值會受定時偏差、整數倍頻偏的影響，為消除或削弱此影響，本文先進行定時估計和整數倍頻偏估計，最后進行小數倍頻偏估計。

2 OFDM同步算法

在文獻[5]所提算法中，雖然利用了CAZAC序列的優良特性[11]實現了定時同步和頻率同步，但是其整數倍頻偏估計要求為4的整數倍時才能進行良好的整數倍估計，為了改善這種限制，本文提出的新訓練序列結構如圖1所示，假設一個OFDM符號長度為N+Ng，其中Ng為cp長度，則新序列長度為2N+Ng。新訓練序列主要由2個相互共軛的CAZAC序列c(k)和c*(k)組成，由文獻[12]知CAZAC序列c(k)可以為：

c(k)=e(jπk2/N)k∈[0,N-1]。

(4)

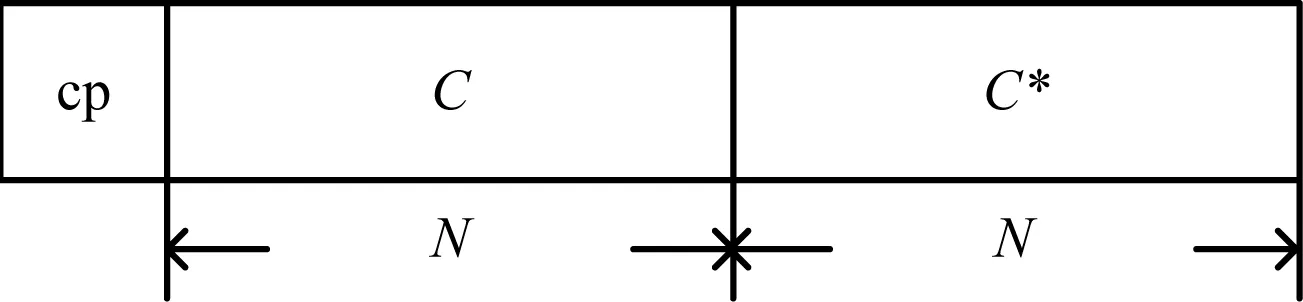
圖1 訓練序列結構

針對第1個CAZAC序列c(k)，其經過信道加入了定時偏差和整數倍頻偏之后，接收到的信號r1(n)為：

r1(n)=c(n)·exp[j2πεi(d+n)/N]= exp(jπn2/N)·exp[j2πε(d+n)/N]=Αexp[jπ(n-(d-εi))2/N],

(5)

式中，A是一個與n無關的常量。由式(5)可以看出，忽略定時偏差d與cp長度Ng，整數倍頻偏會導致CAZAC序列循環左移εi位，從而導致接收信號與接收端的本地CAZAC序列c(k)互相關峰位置的移位。同理可得針對第2個CAZAC序列，整數倍頻偏會導致CAZAC序列循環右移εi位。利用接收端本地序列c(k)和c*(k)，可以得到2個定時度量函數：

(6)

(7)

由式(6)和式(7)2個度量函數可以得到：

(8)

(9)

由式(5)及前面的分析，可得定時偏差d和整數倍頻偏εi的估計為：

(10)

由式(10)可以修正定時偏差與整數倍頻率偏差。當定時偏差得到準確的修正時，小數倍頻偏εf估計為：

(11)

3 算法仿真分析

在仿真過程中，由于考慮地面移動通信與衛星通信網絡的融合，所以仿真所用的OFDM系統參照目前LTE系統中帶寬為5 MHz時的參數設置：IFFT的長度為512，循環前綴cp長度為40個采樣點，QPSK調制方式，引入的定時偏差為50個采樣點，引入的頻率偏移為相對于子載波間隔的歸一化頻偏20.28，仿真所用信道分別為加性高斯白噪聲信道和文獻[13]中的channel Model C類衛星信道，對1 000個子幀進行仿真，其中每個子幀有10個OFDM符號。本文用符號定時偏差捕獲概率和整數倍頻偏捕獲概率來衡量定時算法和整數倍頻偏估計算法的性能，使用定時同步算法仿真定時偏差捕獲概率的結果如圖2所示。

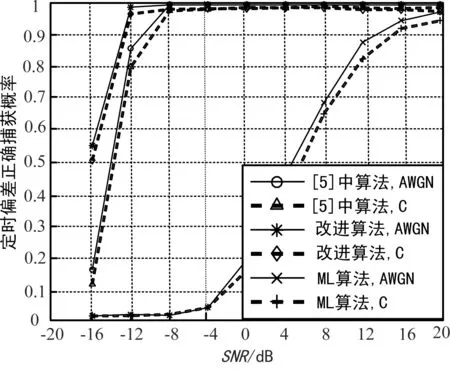
圖2 定時偏差估計算法性能比較

從圖2可以看出，ML定時同步算法在信噪比SNR小于16 dB時性能較差，定時偏差捕獲概率小于90%，而且在衛星信道低信噪比時，ML定時算法性能太差導致算法幾乎不可用。當SNR>-8 dB時，文獻[5]和本文所改進的定時同步算法在高斯信道和Model C類衛星信道下具有很好的定時偏差捕獲性能，正確捕獲概率一直大于90%，且捕獲概率幾乎保持不變。這是因為CAZAC序列具有很好的自相關性，其自相關峰值尖銳，可以很好地克服噪聲的影響，SNR=-8 dB時，改進算法的定時性能已經達到所設計的新訓練序列的上限。由于Model C類衛星信道有直射路徑信號分量，導致在這類信道下的定時偏差捕獲性能與高斯信道時的性能很接近。而且由于本文所改進算法使用的CAZAC訓練序列更長，所以在SNR<-4 dB時，改進算法比文獻[5]的算法性能更好。這說明在衛星信道的低信噪比條件下，改進算法的定時同步性能相比其他兩種算法更好。

使用頻率同步算法仿真整數倍頻偏捕獲概率的結果如圖3所示，可以看出在低信噪比(SNR<-4 dB)時，本文所改進的整數倍頻偏估計算法比其他2種算法的性能都好。

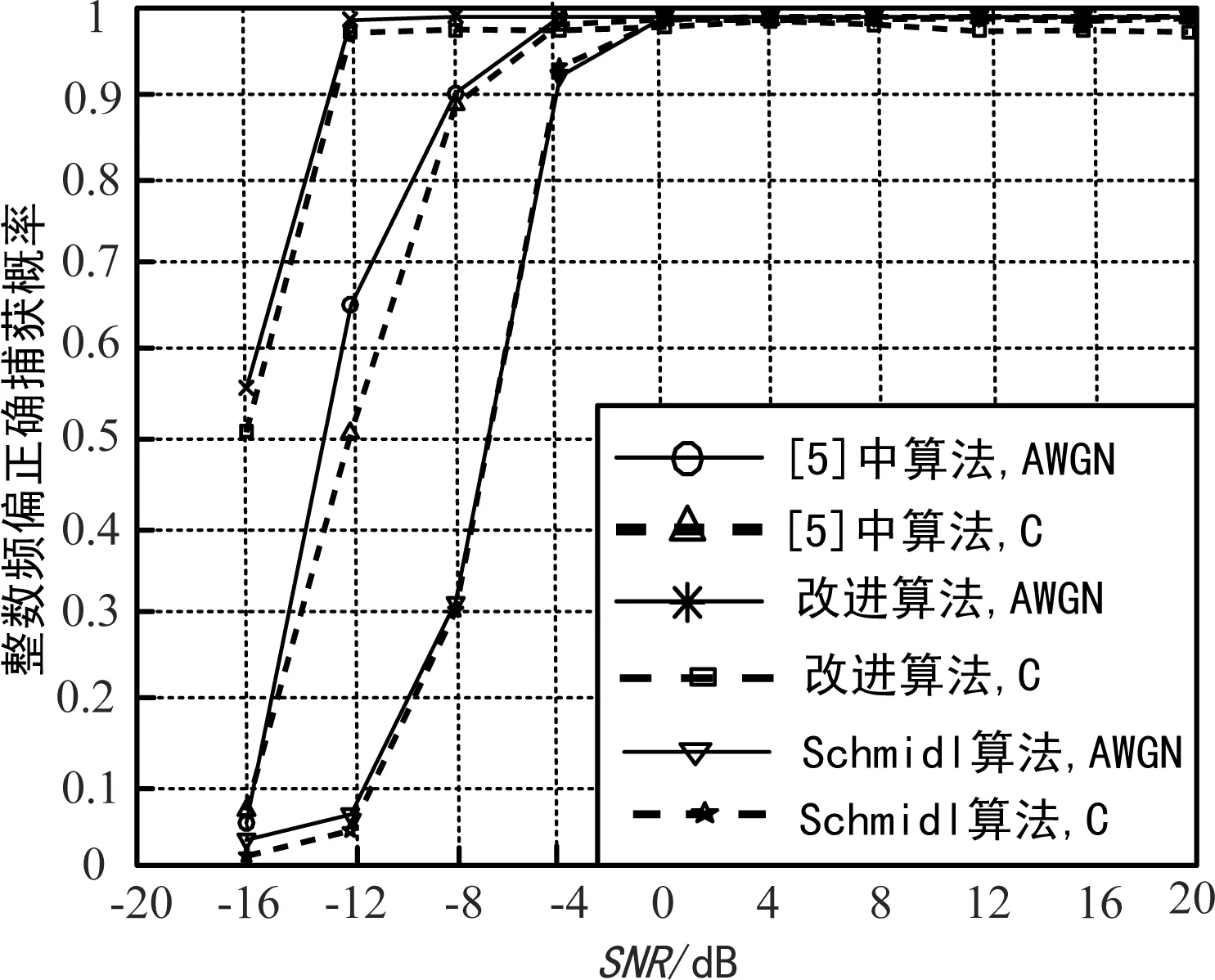
圖3 整數倍頻偏估計算法性能比較

在2種信道中，當SNR>-12 dB時，改進的算法整數倍頻偏正確捕獲概率在很接近1，說明改進的整數倍頻偏估計算法可以更好地適用于衛星信道低信噪比條件。由于改進的整數倍頻偏算法也是利用CAZAC序列的相關性來進行估計整數倍頻偏，所以與定時估計算法類似，SNR=-12 dB時，改進算法的整數倍頻偏估計性能已經達到所設計的新訓練序列的上限。此外，與文獻[5]中算法相比，改進算法不要求整數倍頻偏為4的整數倍才可以取得較好的估計性能；而Schmidl算法必須在SNR=0 dB以上時才有較好的整數倍頻偏估計性能，并且Schmidl算法對定時同步性能較差。當SNR>0 dB時，3種整數倍頻偏估計算法的性能很接近。

當已經對定時偏差進行了準確估計并補償后，可以利用本文所提的新訓練序列進行小數倍頻偏估計，本文使用小數倍頻偏估計均方誤差MSE來衡量算法估計性能，算法仿真結果如圖4所示。從圖4可以看出，在高斯信道下，改進算法的小數頻偏估計性能要比另外2種算法性能更好，但是文獻[5]算法和Schmidl算法受衛星信道的多徑影響很小，而改進算法會受到衛星信道的多徑影響，導致改進算法在信噪比SNR<5 dB時的性能比文獻[5]中的算法稍差，但是當SNR>5 dB時，由于改進算法使用的訓練序列更長，所以它的小數倍頻偏估計性能依舊好于其他2種算法。

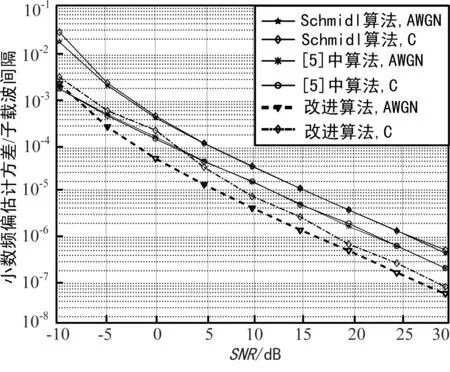
圖4 小數倍頻偏估計算法性能比較

4 結束語

針對OFDM系統對同步的嚴格要求，本文根據CAZAC序列的特性，通過設計新的訓練序列，提出了一種適用于衛星多徑信道低信噪比條件下改進的同步算法，只需在時域信號中就可以利用訓練序列實現定時同步和頻率同步，復雜度較低。仿真結果表明，改進算法克服了文獻[5]算法中要求整數倍頻偏為4的整數倍才有較好同步性能的條件，并且在衛星多徑信道低信噪比條件下，改進算法在定時偏差和整數倍頻偏估計性能上都有較大提升，在小數倍頻偏估計方面性能也良好。因此，改進算法更適用于實際衛星多徑信道低信噪比條件。

[1] Jan-Jaap V D B,Sandell M,Borjesson P O.MLEstimation of Time and Frequency Offset in OFDM Systems[J].Signal Processing IEEE Transactions on,1997,45(7):1800-1805.

[2] Schmidl T M,Cox D C.Robust Frequency and Timing Synchronization for OFDM[J].Communications IEEE Transactions on,1997,45(12):1613-1621.

[3] Minn H,Bhargava V K.ASimple and Efficient Timing Offset Estimation for OFDM Systems[C]∥ IEEE Vehicular Technology Conference,IEEE,2000(1):51-55.

[4] Yun H K,Song I,Yoon S,et al.An Efficient Frequency Offset Estimator for OFDM Systems and Its Performance Characteristics[J].Vehicular Technology IEEE Transactions on,2001,50(5):1307-1312.

[5] 劉 晶,熊春林,魏急波.多徑衰落信道下的OFDM時頻聯合同步算法[J].通信技術,2015,48(4):386-391.

[6] 馬云思,周三文,閆朝星.多徑信道下的OFDM定時同步檢測方法[J].無線電工程,2016,46(4):39-42.

[7] 彭 端,尹長川,樂光新.高速移動環境下OFDM系統載波同步[J].無線電工程,2006,36(1):33-35.

[8] 李 莉.MIMO-OFDM系統原理、應用及仿真[M].北京:機械工業出版社,2014.

[9] 關慶陽.低軌寬帶衛星移動通信系統OFDM傳輸技術研究[D].黑龍江:哈爾濱工業大學,2011.

[10]林 云,張紅帥,劉向玉.一種改進的基于訓練符號的OFDM同步算法[J].無線電通信技術,2012,38(1):38-40.

[11]Boemer L,Antweiler M.Perfect N-phaseSequences and Arrays[J].IEEE Journal on Selected Areas in Communications,1992,10(4):782-789.

[12]朱 彥,張會生,駱艷卜.基于CAZAC序列的OFDM時頻同步算法[J].計算機仿真,2009,26(11):130-133.

[13]ITU-R.Guidelines for Evaluation of Radio Transmission Technologies for IMT-2000[R].ITU-R,Tech.Rep.M.1225,1997.

Research on Synchronization Algorithm for Satellite OFDM System

LIAO Wei-cheng,ZHU Li-dong

(National Key Laboratory of Science and Technology on Communications,UESTC,Chengdu Sichuan 611731,China)

The timing offset and frequency offset may cause a serious performance degradation of OFDM system.This paper studies the synchronization technology of satellite OFDM system to make OFDM suitable to low signal-to-noise ratio of satellite channel for fusion of space-ground integrated communication network.By analyzing OFDM symbol timing synchronization algorithm and and carrier frequency synchronization algorithm in the existing satellite channel condition,this paper designs a novel training sequence based on influence of timing offset and frequency offset on CAZAC sequence correlation peak location,and puts forward an improved synchronization algorithm based on novel training sequence.The simulation results show that the algorithm has higher symbol timing synchronization and carrier frequency synchronization performance with the low signal to noise ratio in satellite channel,and achieve synchronization in the time domain signal synchronization is achieved,compared with other synchronization algorithms in the frequency domain,its complexity is reduced.

OFDM;symbol timing synchronization;carrier frequency synchronization;satellite channel

10.3969/j.issn.1003-3114.2017.01.04

廖為城，朱立東.衛星OFDM系統的同步算法研究[J].無線電通信技術,2016,43(1):15-18.

2016-09-20

國家高技術研究發展計劃(863計劃)項目(2012AA01A502)；四川省科技廳資助項目(2014GZX004)

廖為城(1990—)，男，碩士研究生，主要研究方向：衛星移動通信與地面通信網絡融合。朱立東(1968—)，男，教授，主要研究方向：無線與衛星通信系統的信號處理、信道建模與仿真、資源管理及移動性管理等技術。

TN92

A

1003-3114(2017)01-15-4