移動流量特征模型研究與分析

許 朝，謝人超，黃 韜，劉 江，張云勇

(1.北京未來網絡科技高精尖創新中心，北京 100124；2.北京郵電大學 網絡與交換國家重點實驗室，北京 100876；3.中國聯合網絡通信集團有限公司研究院，北京 100032)

移動流量特征模型研究與分析

許 朝1，2，謝人超1，2，黃 韜1，2，劉 江1，2，張云勇3

(1.北京未來網絡科技高精尖創新中心，北京 100124；2.北京郵電大學 網絡與交換國家重點實驗室，北京 100876；3.中國聯合網絡通信集團有限公司研究院，北京 100032)

不斷增加的移動數據流量給運營商的網絡帶來了前所未有的挑戰，因此，準確地表示網絡流量特征對于合理規劃網絡結構和配置網絡資源有著重要意義。主要介紹移動網絡流量特征模型，并對現網數據進行分析，得出網絡流量概率密度服從對數正態分布，在未來網絡架構的設計中可作為數據輸入模型，用于網絡進行仿真和性能驗證。

移動網絡；流量分布；流量模型；流量概率密度

0 引言

隨著通信技術的發展和用戶需求的不斷提高，越來越多的移動業務和應用場景不斷涌現，使得移動網絡流量呈現出爆炸式的增長。同時，智能終端的普及以及可穿戴設備、智慧城市、智慧家居、數字健康、機器通信(Machine-to-Machine，M2M)等業務的出現，也加劇了網絡流量增長。Cisco公司的統計預測數據表明，預計到2020年，智能手機流量將超過PC端流量，占總流量的30%；電視、平板電腦、智能手機和M2M(machine-to-machine)產生的流量將分別以17%、39%、58%和44%的年復合增長率增長；Wi-Fi和移動設備產生的IP流量將占總流量的66%[1]。

網絡流量的增長速度，特別是視頻流量的增長,遠遠超過了摩爾定律和路由性能提升的速度，為應對這種情況，各個組織、地區與國家已經啟動了第五代移動通信(5G)網絡的研究，諸如歐盟的METIS項目與5GPPP合作研究項目、中國IMT-2020(5G)推進組，國際電信聯盟的ITU-R2020工作組以及韓國的5G論壇等。同時，中國移動、西班牙電信、AT&T、華為、愛立信與阿爾卡特朗訊等運營商與設備商也先后發布了5G白皮書和技術研究報告，業界關注的重點主要從網絡架構、技術創新以及業務應用場景等方面開展研究。

無論是工業界還是學術界的研究人員都越來越意識到現網數據分析的重要性，并將數據的建模和分析結果用于網絡優化和下一代網絡的設計當中[2]。因此，對于移動網絡流量特征的提取和分析成為網絡規劃和設計中的重要參考因素。本文將重點介紹當前主要的移動網絡流量特征模型，并對現網流量進行分析，驗證符合實際網絡流量的特征模型，最后對研究內容做簡單總結。

1 流量特征模型

不斷增加的移動數據流量給運營商的網絡帶來了巨大的挑戰，因此，準確地表示網絡流量特征對于合理規劃網絡結構和配置網絡資源有著重要意義。目前，流量特征模型包括空間泊松點過程模型、對數正態分布模型、指數分布模型、高斯分布模型以及離散余弦變換模型等。本節將主要介紹以上幾種模型。

1.1 空間泊松點過程模型(Spatial Poisson Point Process，SPPP)

SPPP主要應用于基站的位置建模和分析用戶位置的隨機特性，其中，均勻SPPP模型是蜂窩網絡分析中常見的隨機幾何模型，該模型中用戶分布服從均勻分布，是最簡單而且在仿真研究中使用最為廣泛的模型之一。均勻SPPP模型能夠很好地反映相互獨立條件下隨機點的分布情況。

假設SPPP強度為λ，B={B1,B2…Bk}是互不相交的Borel集，N(B)={N(B1),N(B2)…N(Bk)}是獨立隨機變量，用來表示在任何有界的Borel集B中點的數量。某個區域中用戶數量可表示為：

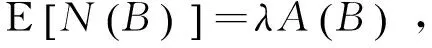
(1)

式中，A(B)表示區域，在區域A(B)中N(B)服從強度為λA(B)的泊松分布。在Borel集B中存在k個點的概率可表示為：

(2)

由于實際用戶分布并不服從均勻分布，均勻SPPP分布無法表示用戶分布的隨機性。與均勻SPPP不同，非均勻SPPP用來描述某個區域的聚集現象，在Borel集B中存在k個點的概率可表示為：

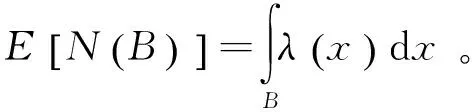
(3)

為表示用戶的非均勻分布，文獻[3]基于均勻SPPP分布提出了修正的Matern模型，在該模型中，首先生成一個均勻SPPP分布的集群中心，然后以集群中心的每個點為圓心，以預設值r為半徑的范圍內生成用戶位置，這些用戶分布服從均勻SPPP分布。其中，預設值r以及每個集群中平均用戶數需要預先確定以保證整體的用戶密度和均勻分布中一致。

在小區非空閑狀態，均勻用戶分布概率(PH)可用式(4)表示，非均勻用戶分布概率(PI)可用式(5)表示：

(4)

PI≈1-e-(1-e-ρR2π)，

(5)

式中，R為小區的半徑，r為集群中心的預設半徑，ρ為用戶密度。

此外，文獻[4]分別對密集城區、普通城區以及郊區3個地區做了研究，結論表明SPPP模型只適用于普通城區和郊區，而密集城區則用Matern模型更為合適。

1.2 對數正態分布模型(LogNormalDistributionModel)

如果隨機變量的對數服從正態分布，那么隨機變量就服從對數正態分布。文獻[5]通過對現網數據的測量和分析表明：流量密度可用對數正態分布近似表示。由于流量分布在時間和空間上的不固定性，文獻還分析了流量在空間上的相關性，并結合對數正態分布提出了一種空間流量模型。

該模型中，區域被劃分為M×N個像素區域，給定像素區域gm,n(m=1,2…M,n=1,2…N)的流量密度為ρm,n/(bytes/km2)，假設ρ=(ρm,n)m-1…M;n-1…N表示流量密度矩陣，xm,n,ym,n為二維笛卡爾坐標，生成高斯隨機分布矩陣：

(6)

式中，和il、jl為(0,ωmax)之間的均勻隨機變量，ωmax用來決定隨機波動率，φl、ψl為(0,2π)之間的均勻隨機變量。得到式(6)之后，可根據式(7)生成對數正態分布矩陣。通過控制σ、μ可調節ρ的大小，使之與特定區域的流量密度相符。

(7)

此外，文獻[6]對E-Plus在德國某個城市的流量數據分析之后指出，這些數據得到的流量密度并不服從均勻分布。Gotzner和Michalopoulou的研究表明，在一段特定的時間內，不同2G小區中的語音業務量可以用對數正態分布來描述[6]，并且在不同小區中GPRS和EDGE的數據流量可以用混合的對數正態分布來近似表示[7]。

1.3 指數分布模型(Exponential Distribution Model)

文獻[8]對不同地區蜂窩網絡流量數據進行了分析結果表明，隨著與市區中心距離的增大，流量密度以指數形式遞減。對市中心流量密度經行歸一化之后，流量密度可表示為：

p(d)=e-d/k，

(8)

式中，d為距離市中心距離，單位為km，k為遞減參數，且隨著地理位置的不同而不同。但需要注意的是，指數模型只適用于城區，并不具有普適性，無法反應流量密度與距離的關系。因此，在流量的空間分布上，文獻[8]使用了指數線性模型式(9)和分段線性模型式(10)對不同地區的流量密度進行了研究，結果表明，這2種模型相對于指數模型來說更能反應流量密度與距離的關系，其中C和D為常數。

(9)

(10)

1.4 高斯分布模型(Gaussian distribution model)

二維高斯分布模型可近似表示移動蜂窩網絡中用戶的分布情況，用戶密度可表示為：

(11)

式中，(x,y)為用戶位置，η可通過對比實驗仿真結果來確定，根據每個小區，可動態調整均值μ1、μ2和標準差σ1、σ2，生成包括均勻分布和非均勻分在內的適用范圍更廣的分布模型。

文獻[9]使用二維高斯分布模型模擬移動網絡中的用戶分布情況，研究了各個參數取不同值時對網絡容量的影響。通過文獻[10]中的方法計算小區間的平均干擾和反向鏈路容量，并與文獻[11]中的模型進行了對比，結果表明使用高斯分布模型對于大型WCDMA網絡的規劃速度更快，準確度更高。

1.5 離散余弦變換模型(DiscreteCosineTransformModel)

文獻[12]對國內某地區一周的的現網流量做了研究，通過對密集城區、普通城區和郊區三種區域流量特征的分析提出了截斷二維離散余弦變換模型，其表達式如下：

(12)

具體參數含義如表1所示。

表1 截斷二維離散余弦變換模型參數含義

1.6 模型對比

從前文的介紹可以看出不同的模型具有不同的適用范圍和特征，具體區別如表2所示。

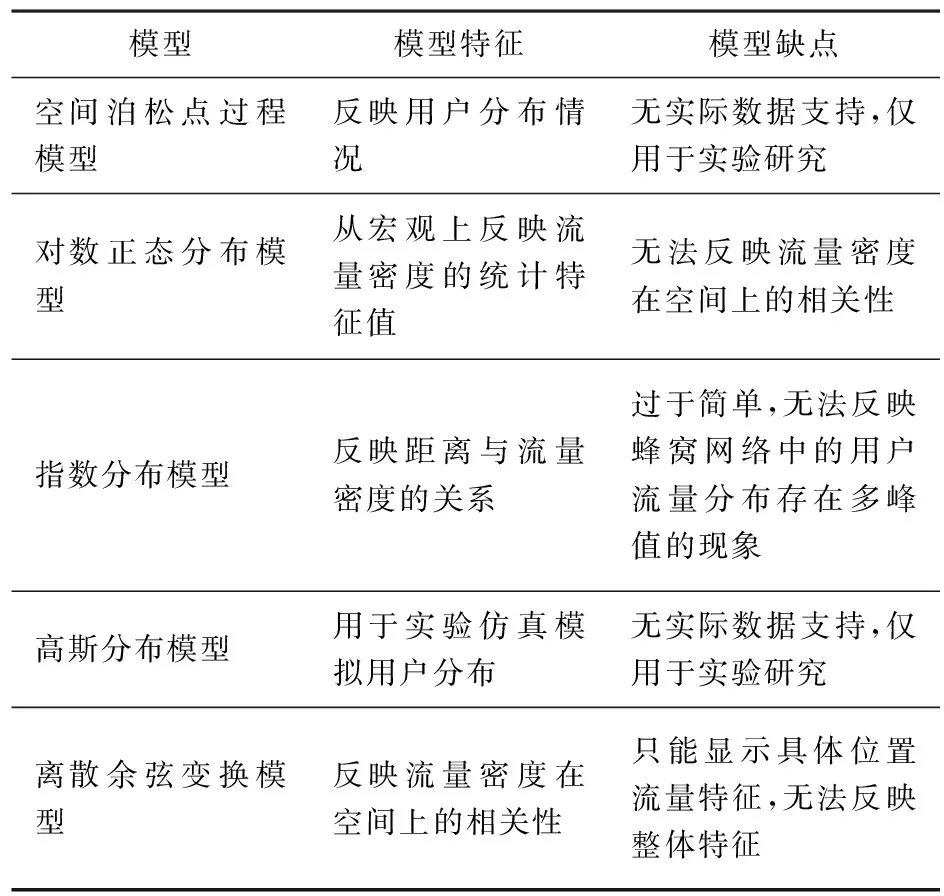
表2 流量特征模型對比

2 數據分析

本文采集了國內某運營商在某市一周的移動網絡流量數據，地理位置涵蓋整個城市，包括67 610個基站的流量數據及經緯度地理坐標。采用網格化的方法將所在地區分為面積相等的小網格，每個網格的面積是0.009 550 8 km2，同一區域中的各個基站流量大小相加作為本區域整體的流量大小，并假設網格內流量均勻分布。由于地理分布上不是一個規則的矩形，本文用MATLAB中的nonzeros函數來去除掉無效區域，得到圖1所示的網絡流量概率密度分布圖，該圖描繪了平均流量密度的分布情況。

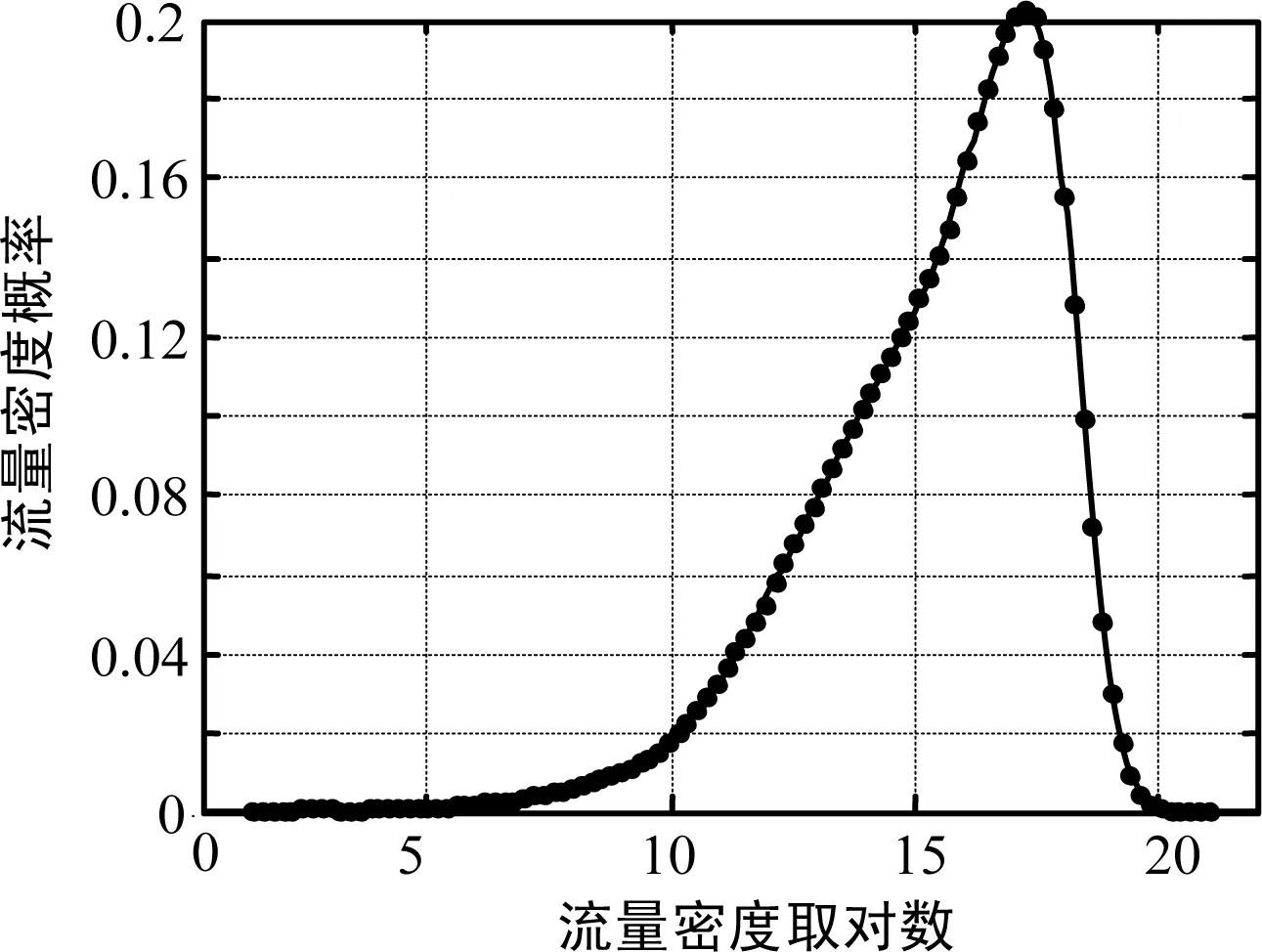
圖1 整體網絡流量密度概率分布

結果顯示對數正態分布與數據最為吻合，擬合函數如下：

(13)

擬合函數中SSE(方差和)取值為0.000 017 38，接近于0；相關系數為0.999 9，接近于1，整體擬合效果較為理想，擬合參數如表3所示。

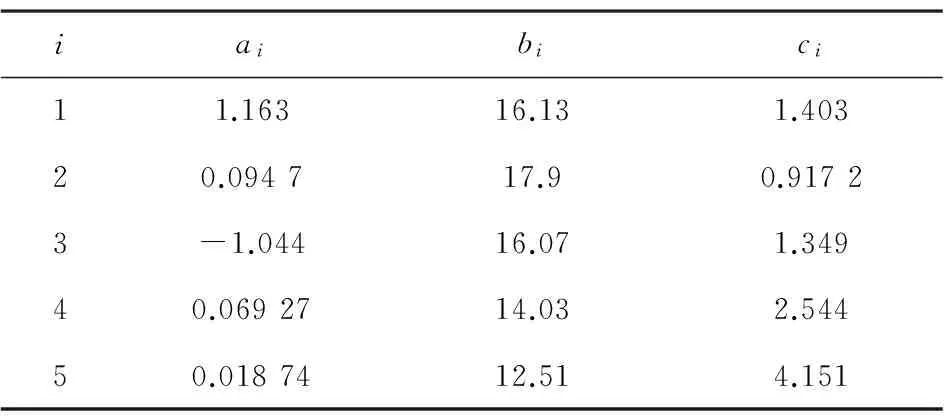
表3 擬合參數

在對該地區選取的住宅區、商業區和辦公區3個區域進行同樣的分析之后得到圖2、圖3和圖4的結果。

仿真分析表明這3個地區流量概率密度均服從對數正態分布。因此，無論是整體流量密度還是局部流量密度均可用式(14)表示，通過調節N可得到不同的流量特征。

(14)

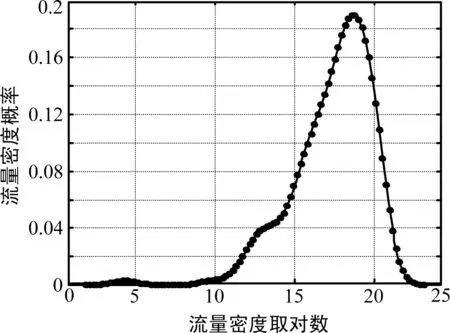
圖2 住宅區流量密度概率分布

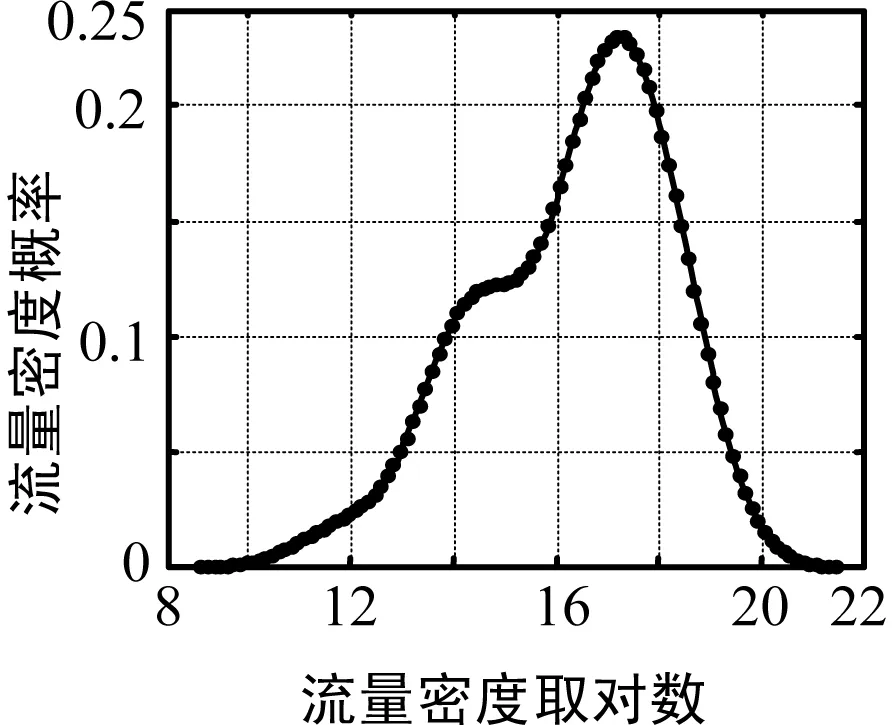
圖3 商業區流量密度概率分布

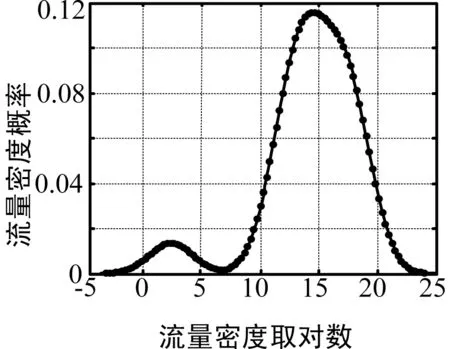
圖4 辦公區流量密度概率分布

3 結束語

本文主要對主要的移動網絡流量特征模型做了簡單介紹，并對不同模型的適用范圍和缺點作了總結和對比。通過對現網數據的處理和分析，得到了符合實際的移動網絡流量特征模型。

結果表明，無論是整體流量概率密度還是局部流量概率密度，均服從對數正態分布。因此在未來網絡設計中進行數據驗證時可采用對數正態分布模型模擬網絡流量，從而驗證網絡相關性能是否滿足設計要求，對于未來網絡的規劃和設計都具有重要意義。

[1] Cisco Visual Networking Index: Forecast and Methodology,2015-2020.[DB/OL].http:∥www.cisco.com/c/dam/en/us/solutions/collateral/service-provider/visual-networking-index-vni/complete-white-paper-c11-481360.pdf.

[2] 周 軒.下一代移動通信網絡中的業務特征認知及服務機制研究[D].杭州：浙江大學,2015.

[3] Vidacs A,Godor I.Power Saving Potential in Heterogeneous Cellular Mobile Networks[C]∥Personal,Indoor and Mobile Radio Communications(PIMRC).IEEE,2011:2412-2414.

[4] Zhang J,Wang W,Zhang X,et al.Base Stations from Current Mobile Cellular Networks: Measurement,Spatial Modeling and Analysis[C]∥Wireless Communications and Networking Conference Workshops (WCNCW).IEEE,2013:1-5.

[5] Lee D,Zhou S,Zhong X,et al.Spatial Modeling of the Traffic Density in Cellular Networks[J].IEEE Wireless Communications,2014,21(1): 80-88.

[6] Gotzner U,Rathgeber R.Spatial Traffic Distribution in Cellular Networks[C]∥Proc.VTC,1998,3(5)：1994-1998.

[7] Michalopoulou M,Riihijarv J,Mahonen P.Towards Characterizing Primary Usage in Cellular Networks: A Traffic-based Study[C]∥New Frontiers in Dynamic Spectrum Access Networks(DySPAN).2011 IEEE Symposium,2011: 652-655．[8]AlmeidaS,QueijoJ,CorreiaLM.SpatialandTemporalTrafficDistributionModelsforGSM[C]∥Proc.IEEEVTS50thVehicularTechnologyConference,1999,1(9):131-135.

[9]SonN,RobertA.ApproximatingUserDistributionsinWCDMANetworksUsing2-DGaussian[C]∥InternationalConferenceonComputing,CommunicationsandControlTechnologies,2005：1-5.

[10]AklR,HegdeM,Naraghi-PourM,etal.Multi-cellCDMANetworkDesign[C]∥IEEETransVehTechnol,2001,50(5):711-722.

[11]AklR,ParvezA.ImpactofInterferenceModelonCapacityinCDMACellularNetworks[C]∥ProceedingsofSCI04:CommunicationandNetworkSystems,TechnologiesandApplications,2004,3(7):404-408.

[12]GuanL,ZhangX,LiuZ,etal.SpatialModelingandAnalysisofTrafficDistributionBasedonRealDatafromCurrentMobileCellularNetworks[C]∥IEEE,2013：135-138.

Research and Analysis of Mobile Traffic Model

XU Chao1，2,XIE Ren-chao1，2,HUANG Tao1，2,LIU Jiang1，2,ZHANG Yun-yong3

(1.Beijing Advanced Innovation Center for Future Internet Technology,Beijing 100124;2.Beijing University of Posts and Telecommunications,Beijing 100876;3.China Unicom Research Institute,Beijing 100032)

Increasing mobile traffic has brought great challenges to the operators’ network.It is significant to describe the features of traffic accurately fornetwork structure design and network resources configuration.In this paper,several mobile spatial traffic modelsare introduced and real network traffic data is analyzed.Result shows that the traffic probability density follows lognormal distribution which can be used as the input data model in future network designfornetwork simulation and performance validation.

mobile network;traffic distribution;traffic model;traffic probability density

10.3969/j.issn.1003-3114.2017.01.02

許 朝，謝人超，黃 韜，等.移動流量特征模型研究與分析[J].無線電通信技術,2017,43(1):07-10,22.

2016-09-02

國家高技術研究發展計劃(863計劃)項目(2015AA016101)；國家自然科學基金項目(61501042)；北京市科技新星計劃項目(Z151100000315078)；北京郵電大學青年科研創新計劃專項(2015RC10)

許 朝(1993—)，男，碩士研究生，主要研究方向：未來網絡關鍵技術、內容中心網絡、網絡緩存等。張云勇(1976—)，男，博士后，中國聯通研究院副院長，北京郵電大學兼職教授，主要研究方向：云計算、移動互聯網、融合網絡技術等。

TN915

A

1003-3114(2017)01-07-4