臨近空間非彈道式機動模式與跟蹤濾波問題

李君龍，秦雷，謝曉瑛

(北京電子工程總體研究所，北京 100854)

臨近空間非彈道式機動模式與跟蹤濾波問題

李君龍，秦雷，謝曉瑛

(北京電子工程總體研究所，北京 100854)

由于美國近些年來在臨近空間高超聲速飛行器領域給世界各國帶來了巨大的安全威脅，它的高速和機動特性給地面防御系統帶來了巨大的困難，引起了其他國家的廣泛關注。在該領域的關鍵技術中，非彈道式機動跟蹤濾波問題是尚未攻破的技術瓶頸。介紹了臨近空間目標3種典型的非彈道式機動模式，并且從不同機動模式跟蹤濾波方法、機動模式未知情況下的跟蹤濾波方法、多種機動模式組合的跟蹤濾波方法3個方面進行了探討，最后針對非彈道式跟蹤濾波問題及應對措施進行了闡述。

非彈道式；臨近空間;機動模式；跟蹤濾波；預測；彈道軌跡

0 引言

美國近些年來發展臨近空間進攻型武器力度不斷加深，引起了世界各國的廣泛重視。許多國家相應開展了臨近空間防御技術研究，并已開始著手進行相關基礎設施建設工作，不斷加深對防御技術探索力度。在臨近空間防御體系中，目前存在著許多技術問題，其中非彈道式機動濾波問題作為一項最為棘手的問題之一，受到了世界各國的廣泛關注。本文從介紹臨近空間高超聲速飛行器國外發展態勢、臨近空間高速目標特征及防御難點、臨近空間目標非彈道式機動模式跟蹤濾波方法、非彈道式跟蹤濾波問題及應對措施4個方面入手，對臨近空間目標非彈道式機動模式跟蹤濾波問題進行了剖析，以期對未來構建臨近空間防御體系提供一些借鑒。

1 臨近空間高超聲速飛行器國外發展態勢

1.1 美國“新三位一體”戰略思想加速了臨近空間武器發展進程

美國陸、海、空三軍曾先后啟動了多個臨近空間武器研制計劃，現已陸續推進至關鍵技術集成演示驗證階段，并相繼轉入武器裝備研發。

美國基于“新三位一體”戰略，加快了臨近空間武器的發展步伐，提出從2000—2020年臨近空間武器的發展計劃， 主要包括“HIFIRE”計劃、“HyFly”計劃、“X-51”計劃、“X-51+”計劃、“HTV-2”計劃、“CSM-2”計劃、“CSM-1”計劃、“AHW”計劃、“ArcLight”計劃。

1.2 臨近空間武器是應對“反介入/區域拒止”的重要手段

臨近空間武器旨在打擊“時敏、高價值、決定性”目標，是美國實行新時期軍事戰略、應對“反介入/區域拒止威脅”的重要手段，在其新一代攻擊體系中占有重要地位。

1.3 臨近空間威脅即將成為現實

美國高超聲速巡航導彈(X-51A)、先進高超聲速武器(advanced hypersonic weapon, AHW)、高超聲速技術飛行器(HTV-2)相繼試驗成功，同時我國周邊國家俄羅斯、印度、日本等國加緊開展臨近空間高超聲速飛行器技術研發。印、俄聯合研制的“布拉莫斯-2”高超聲速巡航導彈計劃于2020年前后進行飛行試驗。

2 臨近空間高速目標特征及防御難點

臨近空間目標飛行高度低，速度快，遠距離探測難，可長時間遠距離機動飛行，彈道預報難度較大，突防能力和打擊范圍大，目標與環境特性復雜，探測跟蹤難，多類目標運動與毀傷特性差異大,導致多模式防御難度較大。

3 臨近空間目標非彈道式機動模式跟蹤濾波方法

3.1 非彈道式機動模式分析

根據臨近空間環境特點，通過設置初始條件建立高超聲速飛行器運動方程，構建以下3種目標機動模式：①維持飛行高度不變，橫向機動最大； ②最大升阻比飛行，側滑角為常數；③常值攻角飛行，側滑角為常數。設定實際高超聲速目標機動模式為3種典型機動模式的交互融合，根據不同機動模式情況、機動模式未知情況、多種機動模式組合情況開展研究臨近空間飛行器非彈道式機動模式跟蹤濾波問題。

3.1.1 非彈道式目標機動模式跟蹤濾波基本原理

在慣性球坐標系下，滑翔彈頭運動方程可以表示為

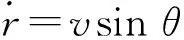
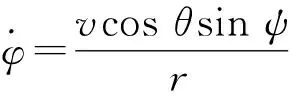
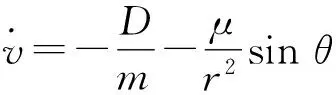
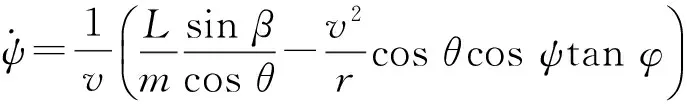
(1)

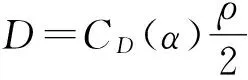
對于不存在氣動力的空間飛行器或中段飛行的彈道導彈彈頭類目標，L=D=0，故式(1)可大幅簡化為

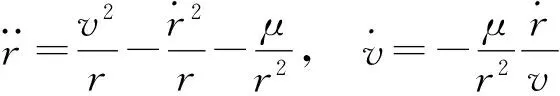
(2)

上述方程與飛行器特征尺寸、重量等因素無關，較容易求解。利用當前速度、位置可以較為方便、準確地估計目標后續飛行軌跡。

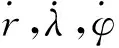
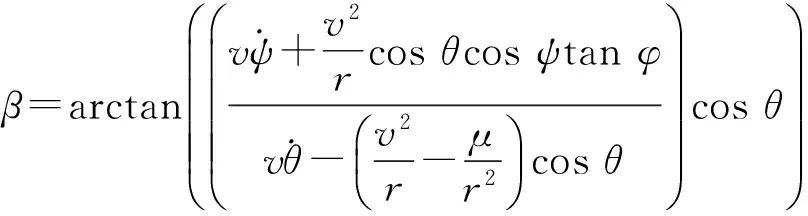
(3)

因此，通過對目標的跟蹤，可獲取控制參數變化規律，并將其與現有目標運動特性模板進行匹配，并通過濾波或參數估計等方法求出模板待定參數，可對目標后續飛行過程進行預報。

3.1.2 目標飛行的可能機動模式

臨近空間目標可通過控制攻角α和側滑角β進行機動。考慮以下幾種典型的機動模式：①維持飛行高度不變，橫向機動最大；②最大升阻比飛行，側滑角為常數；③常值攻角飛行，側滑角為常數。

(1) 等高度飛行，橫向機動最大

根據運動方程可以求解得出

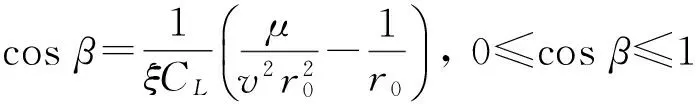
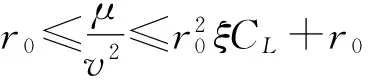
(4)

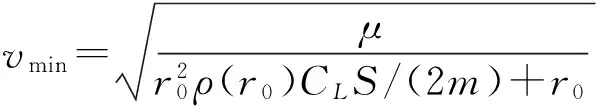
(5)

因此，如果v>vmin，總可以找到參數β，使得目標維持等高飛行。

速度vmin與目標飛行高度r0-Re密切相關。圖1給出了不同升力系數取值情況下維持等高飛行的最小速度隨高度的變化情況。從圖中可以看出，在20 km以下，維持等高飛行的最小速度隨高度的升高變化不大，且受升力系數不確定性的影響相對較小。

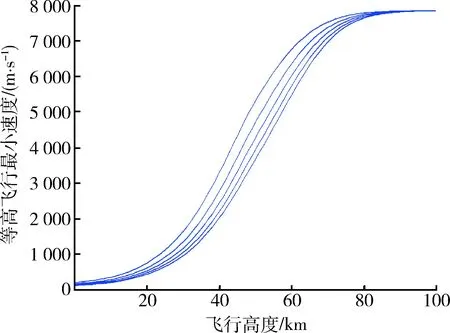
圖1 等高條件下飛行高度與飛行速度關系圖Fig.1 Relationship between flight height and flight velocity under equal height

若v=vmin，為維持等高飛行，需增大飛行攻角，若在最大許用攻角前提下仍然無法滿足v>vmin，則等高飛行難以維系，飛行高度將迅速降低。考慮到由于側向力主要由升力系數和側滑角產生，且近似正比于CLsinβ，為確保側向機動最大，β應盡可能大。

不失一般性，β的選取應使得在CL最大情況下，下式取最小值：

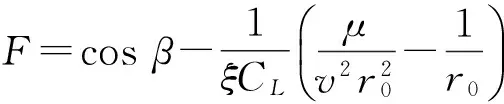
(6)

(2) 最大升阻比飛行，側滑角為常數

針對AHW滑翔彈頭，升阻比η=L/D，假定初始速度為6 km/s，初始時刻飛行高度為90 km，分析得出的典型飛行彈道如圖2～4所示。

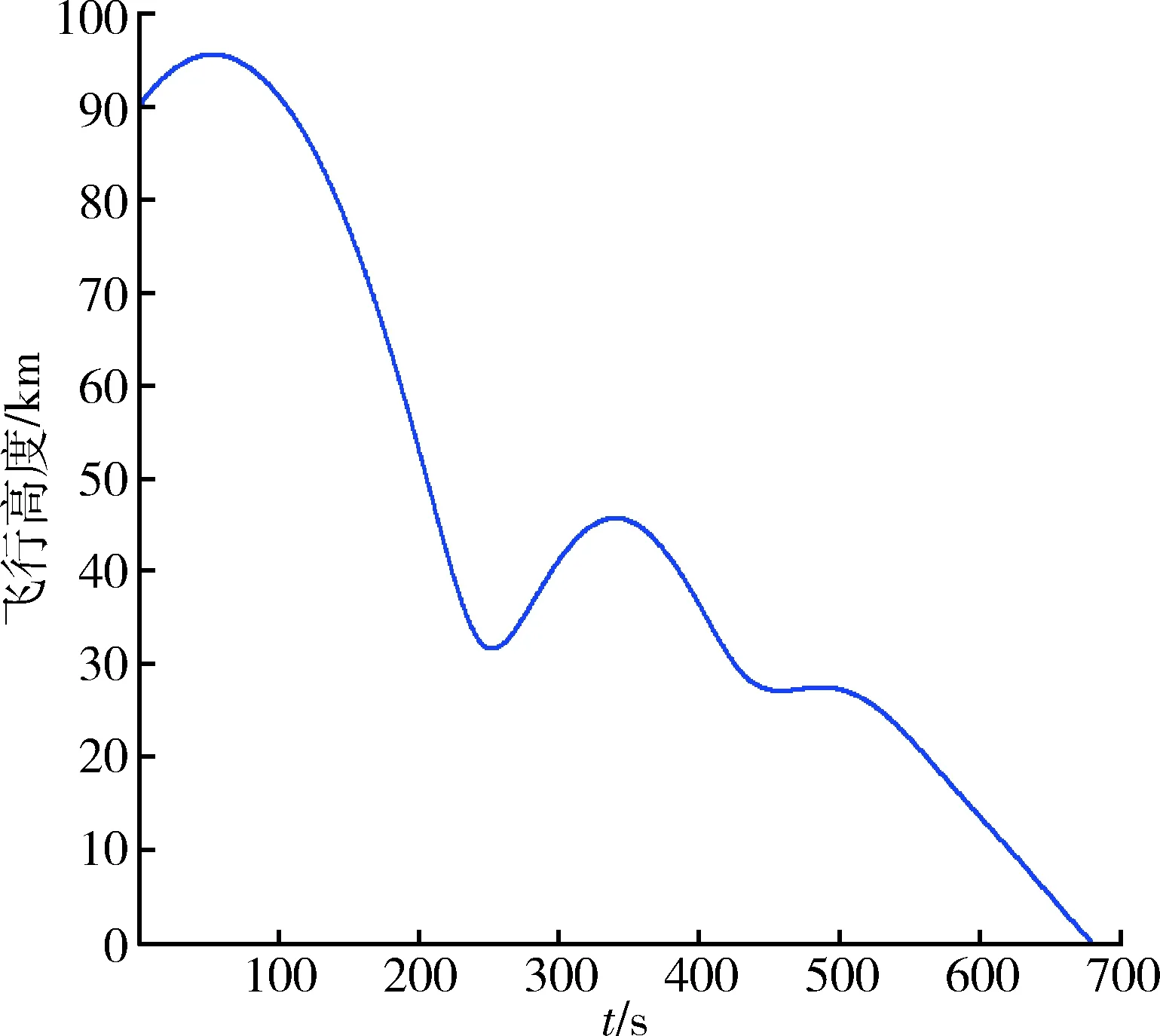
圖2 最大升阻比條件下飛行高度變化示意圖Fig.2 Sketch map of flight height under maximum lift-to-drag ratio

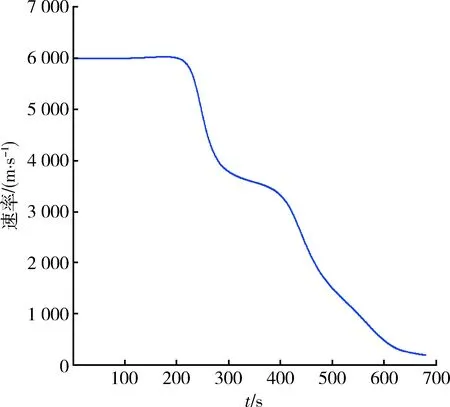
圖3 最大升阻比條件下飛行速度變化示意圖Fig.3 Sketch map of flight velocity under maximum lift-to-drag ratio

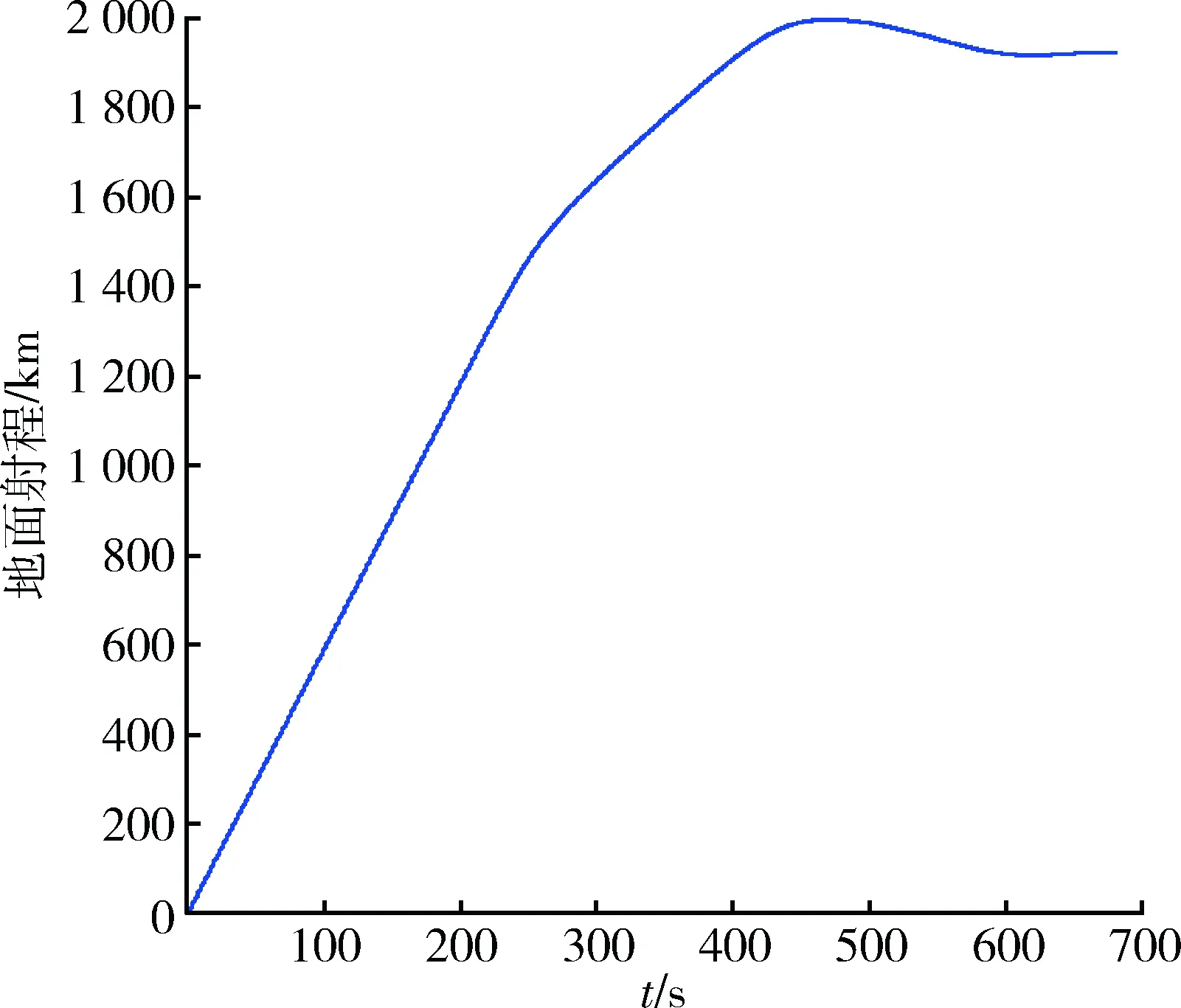
圖4 最大升阻比條件下地面射程變化示意圖Fig.4 Sketch map of ground range under maximum lift-to-drag ratio

(3) 常值攻角飛行，側滑角為常數

針對AHW滑翔彈頭，升阻比η=L/D，假定初始速度為6 km/s，初始時刻飛行高度為90 km，分析得出的典型飛行彈道如圖5～7所示。

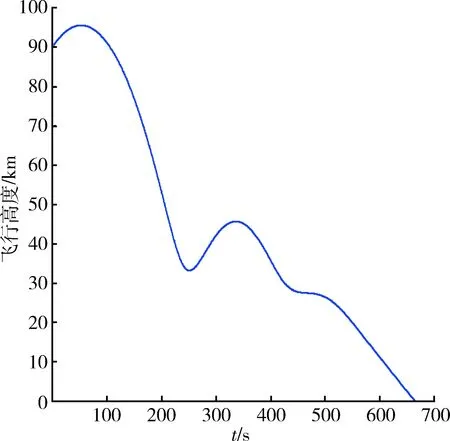
圖5 常值攻角和側滑角條件下飛行高度變化示意圖Fig.5 Sketch map of flight height under constant angle of attack and angle of sideslip

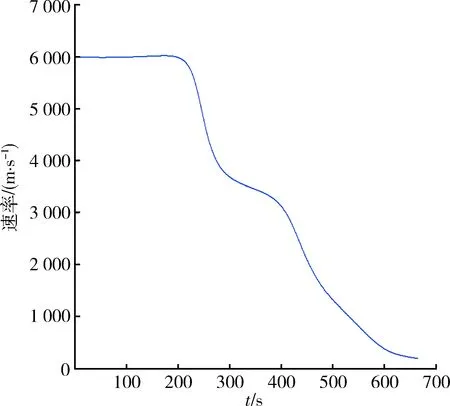
圖6 常值攻角和側滑角條件下飛行速度變化示意圖Fig.6 Sketch map of flight velocity under constant angle of attack and angle of sideslip

圖7 常值攻角和側滑角條件下地面射程變化示意圖Fig.7 Sketch map of ground range under constant angle of attack and angle of sideslip

3.2 不同機動模式跟蹤濾波方法

通過以上建立的3種非彈道式目標機動模式，研究臨近空間飛行器在不同高度，不同馬赫數下作不同模式機動時用不同濾波算法在跟蹤定位臨近空間飛行器上精度差別及誤差大小，主要使用卡爾曼濾波算法、擴展卡爾曼濾波算法、無跡卡爾曼濾波算法、粒子濾波算法、模糊自適應濾波算法、自適應網格算法、固定延遲平滑算法、無跡粒子濾波算法等濾波算法或者使用單一機動目標模型濾波方法。

不同機動模式濾波方法具體步驟如下：通過建立質心運動方程及設計跟蹤濾波器來對3種目標非彈道式機動模式進行跟蹤濾波，在設計跟蹤濾波器時需要考慮3種機動模式的特殊性，比如該機動模式的一些特定條件，包括：等高飛行時橫向機動最大的機動模式要求滿足彈道傾角及彈道傾角的微分為0，攻角取最大值等條件。由于臨近空間目標主要通過控制攻角α和側滑角β進行機動，因此在跟蹤濾波器設計過程中應按照3種機動模式求出攻角α和側滑角β的變化規律，并將其加入跟蹤濾波器運動方程，以實現高精度實時跟蹤不同機動模式的非彈道式目標飛行器。

3.3 機動模式未知情況下的跟蹤濾波方法

當機動模式未知情況下，通過設計跟蹤濾波器使用勻速運動模型、勻加速運動模型、曲線運動模型、勻速轉彎運動模型、Singer模型、半馬爾科夫模型、機動目標“當前”統計模型、Jerk模型等目標機動模型，利用這些模型進行交叉耦合形成交互式多模型跟蹤濾波算法。通過計算得到不同模型的使用概率，從而可以判斷出當前非彈道式目標處于何種機動模式。相比于單一機動模型濾波器來說，會較大程度提高跟蹤濾波精度，為彈道預報、預估下一時刻目標所在位置及速度提供了有力保障。同時還需結合多時鐘濾波器，通過跟蹤探測到每個機動模式轉換時刻，完成機動模式之間平滑過渡，滿足跟蹤定位的需要。

3.4 多種機動模式組合的跟蹤濾波方法

當目標飛行器在以上3種機動模式組合飛行情況下，主要跟蹤濾波步驟如下：首先需要建立坐標系，包括：地心慣性坐標系、發射點慣性坐標系、目標慣性坐標系及目標體坐標系；其次通過將3種機動模式所使用的跟蹤濾波器交叉耦合形成交互式多模型跟蹤濾波器，由于目標的位置由地面目標跟蹤裝置測量得到，設計過程中還要考慮到測量信息數據更新率；然后在地心慣性坐標系下建立質心運動學方程，可以求出目標的彈道傾角、彈道偏角、俯仰角、滾轉角、偏航角。由于臨近空間目標飛行器受到的氣動力主要包括升力、阻力、側向力，在求解目標機動加速度時需要包括由氣動力作用產生的加速度和重力作用產生的加速度，結合多時鐘濾波器，通過跟蹤探測到每個機動模式轉換時刻，實現機動模式之間平滑過渡；同時還要使用衰減濾波器，目的是在濾波過程中逐步削弱舊觀測信息在本次新估計中的作用，也就是使舊的記憶信息在新估計中的作用逐步衰減；最后實現對臨近空間飛行器非彈道式機動模式高精度跟蹤濾波，得到目標位置、速度和加速度估計，為下一步的非彈道式目標軌跡預報提供強有力的支撐。

4 臨近空間飛行器跟蹤、濾波與預報技術的研究現狀及發展趨勢

4.1 國外研究現狀及發展趨勢

目標跟蹤問題實際上就是目標狀態的跟蹤濾波問題，即根據傳感器已獲得的目標量測數據對目標狀態進行精確的估計。機動目標跟蹤模型、跟蹤濾波方法、彈道軌跡預測方法是機動目標跟蹤的關鍵部分，因此以下分別對這3方面的研究現狀和發展趨勢進行概述。

4.1.1 機動目標跟蹤模型研究現狀和發展趨勢

機動目標的跟蹤模型有2種建模方法：一種是根據已知或假定的目標信息構造目標運動模型，如CA(constant acceleration)模型[1]、CV(constant velocity)模型[2]、Singer模型[3]、半馬爾可夫統計模型[4]、高度機動目標Jerk模型[5]等，其中比較典型的是Singer模型。CA，CV模型在目標無機動的情況下，有很好的跟蹤效果，當目標的運動特性復雜時，就會帶來很大的模型誤差。1969年，R. A. Singer提出了機動目標的零均值、一階時間相關機動加速度模型(Singer模型)[6]，該模型表述簡單，對介于勻速和勻加速范圍之間的目標機動，有很好的描述能力。但是Singer模型本質上是一種先驗模型，不能有效地描述目標的隨機機動。1979年，R. L. Moose等提出了具有隨機開關均值的半馬爾科夫模型機動目標統計模型。該模型為保證過程的收斂性，需要大量預先計算的平均值，導致在工程中難以有效應用。1997年，Kishore借鑒 Singer 模型思想， 提出了一種Jerk 模型，并將Jerk表示為一零均值的白噪聲過程，以此可得到對加速度更加精確的估計，從而實現對機動目標的精確跟蹤。對于強機動性的運動目標，利用目標的Jerk描述目標機動更為方便。

另一種建立機動目標跟蹤模型的有效途徑是參數化函數逼近方法[7-8]，該類方法以函數逼近理論為基礎，用含較少待估參數且形式已知的函數或函數組合表示被測真實信號(或系統狀態)，可以顯著增加估計系統的數據冗余。常用函數建模途徑有多項式、樣條、微分方程和經驗公式等。

4.1.2 跟蹤濾波方法研究現狀與發展趨勢

在機動目標跟蹤問題中，為了獲取機動目標的運動參數，就必須運用量測手段測量機動目標的運動狀態。但是，量測值不僅有系統的狀態參數，還包含有量測噪聲。如何從受噪聲污染的量測值中恢復信號或逼近信號，解決這一問題的辦法就是最優估計。大批學者進行了不懈努力，建立和發展了許多有特色的、實用的濾波理論和基本方法，其中高斯、維納、卡爾曼等人做出了重大貢獻。針對目標當前和未來時刻的運動狀態，基于不同的數學統計和數學處理方法，提出和創建的各種經典濾波和預測的基本方法主要有：

(1) 線性濾波方法，主要包含Kalman濾波[9]、α-β與α-β-γ濾波[10]、兩點外推濾波[11-12]和線性自回歸濾波[13-14]。卡爾曼(Kalman)濾波是由R.E.Kalman最早提出的，它是一種線性最小方差估計，采用狀態空間方法，在時域內設計濾波器，算法采用遞推形式。卡爾曼濾波對線性系統的濾波精度高而且計算簡便，它是一種很常用的方法。

(2) 非線性濾波方法。在Kalman濾波基礎上不斷進行改進和完善，促進了非線性濾波方法的發展，比較常用的有：擴展Kalman濾波方法(extended Kalman filter, EKF)[15]、無跡卡爾曼濾波方法(unscented Kalman filter, UKF)[16]、中心差分卡爾曼濾波方法(central difference Kalman filter, CDKF)[17-19]、兩步最優濾波(two-step)算法[20]。以上的濾波算法均是在高斯假設條件下進行應用的，因此均可稱為高斯濾波。雖然擴展EKF，UKF均能適應非線性系統。但當非線性太強時，其濾波性能便會急劇下降，甚至會出現發散。在這種情況下， Carpenter便提出了粒子濾波(particle filter，PF)算法，該算法不受系統線性化誤差或高斯噪聲假設的限定，由于計算量和復雜度的限制，相關研究集中于理論分析和仿真計算，實際系統應用較少。

(3) 自適應濾波方法。可分為3類：檢測自適應濾波方法、實時辨識自適應濾波方法和全面自適應濾波方法。全面自適應濾波方法綜合了檢測自適應濾波方法和實時辨識自適應濾波方法的優點。其基本思想是使用多個不同的運動模型分別匹配目標的不同運動狀態。交互式多模型算法就是其中一種典型方法。目前普遍認為，對高速高機動目標跟蹤，最好的算法是交互式多模型算法，這也是當前的研究熱點。

交互式多模型算法已發展了3代。第1代多模型算法不考慮模型間的切換，屬于靜態的無輸入交互的多模型方法，當系統的結構或參數肯定要發生變化時，有可能導致估計器發散，從而使得估計性能惡化。第2代多模型算法是Blom和Bar-Shalom在廣義偽貝葉斯算法基礎上，提出了一種具有馬爾科夫切換系數的交互式多模型算法(interacting multiple model, IMM)。與一般動態多模型加權混合估計算法不同，它對濾波器的輸入和輸出進行了巧妙的加權綜合。在IMM算法中多個模型并行工作，用馬爾可夫過程描述模型間的轉換，目標狀態估計是多個濾波器交互作用的結果。該方法不需要機動檢測，同時具有全面自適應跟蹤能力。

前2代多模型算法均假設模型集在預先設定之后不再發生變化，所以也被稱為定結構多模型算法。這會導致2個問題，一是過多的模型會導致算法計算量過大；二是過多的模型之間的競爭不僅不能使算法估計性能提高，反而可能使其下降。為解決上述問題，LI Xiao-rong和Bar-Shalom提出了第3代多模型估計理論，即變結構多模型估計。這類算法假設模型集隨著外界條件和實時信息變化，目前已成為一個研究熱點。圍繞復雜機動目標跟蹤問題，多模型跟蹤濾波算法主要集中于模型集選擇、模型交互與在線結構調整策略、特定結構子濾波器的算法設計等方面，特別是在數量精簡、表示能力突出的模型集設計和模型結構的在線調整策略方面，還有待深入研究。

4.1.3 彈道軌跡預測方法研究現狀和發展趨勢

彈道預報就是根據對目標彈道的測量信息估計目標的位置、速度、加速度等信息，并對目標后續時刻的運動軌跡外推預測。國外對于彈道軌跡預測方法的研究集中在彈道導彈(tactical ballistic missile, TBM)方面。就外推算法而言，目前總體上可以分為3類：解析法，數值積分法和函數逼近法。例如，Harlin和 Cicci給出了一種利用狀態轉移矩陣進行彈道導彈彈道預測的方法。該方法使用狀態轉移矩陣修正初始條件導彈的狀態向量，可用于只知道導彈發射點和相撞點的情況；Akgül和Karasoy開發了一個戰術彈道導彈彈道預測的工具，通過衛星或雷達記錄的部分軌道數據通過自適應模型算法推算出完整軌道；Bhowmik和Chandrani使用測量數據修正模型來進行彈道導彈的軌跡預測。該方法使用了標準的非線性模型結構，用EKF算法建立模型修正過程；Charoenpon和Pankeaw提出了一種建立氣動特征方程的方法，用于數字彈道預測。該方法的目的在于建立基于攻角和航行速度的多項式方程。首先假定導彈的參數在一個范圍內變化，然后對導彈進行建模并計算氣動力，得到統計數據后再運用多項式插值得到所有情況下的數值，最后綜合得到特征方程。綜合看來，目前已有的彈道預報方法大多集中在對慣性彈道及其落點的預報上，針對高超聲速機動目標的彈道預測相應的研究還少見報道。

4.2 國內研究現狀及發展趨勢

在目標加速度建模方面，國內學者提出了機動目標當前統計模型，它著重強調機動變化，但要求符合實際的目標機動特性的先驗假設，機動時跟蹤性能較好，非機動時跟蹤精度稍有下降。在多模型濾波算法研究方面，國內學者也進行了大量研究，提出了參數自適應IMM算法、兩級多模型濾波器、強跟蹤多模型估計器，交互式多模型自適應濾波算法以及最好模型提升多模型估計算法等，推動了該領域的理論發展。

在應用背景研究方面，針對反艦導彈末端“蛇形機動”，國內學者設計了變結構自適應網格交互式多模型算法，提高了采用相同初始模型集的固定網格交互式多模型濾波算法在這類運動中的估計精度；針對低空目標跟蹤問題，提出了一種去相關濾波方法來克服多徑誤差相關性的影響，并應用IMM算法來提高跟蹤精度。

國內學者在提高彈道預測精度方面進行了很多研究，主要針對彈道導彈提出了很多高精度算法。劉永蘭等提出一種基于距離信息修正的自由段彈道預測法。該方法是在雷達觀測的彈道導彈自由段運動數據的基礎上，采用滑動窗口中點平滑法處理觀測數據，再次利用距離信息對軌道根數進行動態微分修正，提高觀測數據的利用率和彈道預測的精度。王莎等對動弧平滑平均法，基于距離修正的分段彈道預測法兩種方案進行了研究。此外，董捷和董云峰探討了一種工程應用，即將改進灰色預測模型引入TBM彈道預測問題，仿真結果顯示在短時間內預測軌跡精度較高，隨著時間的增長需要加入新的觀測數據，利用新陳代謝模型進行預測。

國內學者還對彈道預測問題的誤差進行了一些研究。楊皓云等分析驗證了地球旋轉對TBM彈道預測的影響。趙鋒等提出了一種簡單高效的誤差計算方法。文中基于所建立的輔助坐標系，通過一系列坐標變換對彈道導彈中段防御預警系統的彈道預測過程進行了合理分解，在此基礎上對跟蹤雷達正弦坐標系下彈道預測的誤差進行了分析，給出了誤差的工程計算方法和蒙特卡羅仿真結果。

關于機動目標預測問題，郭躍等從來襲導彈機動模型的選取出發,結合無跡卡爾曼濾波算法的推算,建立了來襲導彈彈道預測的仿真模型。同時結合實例，對來襲導彈彈道預測的卡爾曼濾波算法和無跡卡爾曼濾波算法進行了仿真比較。

4.3 國內外研究現狀及發展趨勢對比分析

在機動目標跟蹤與預報方法方面，國外學者建立了諸如Singer,Jerk等多種機動模型，提出了著名的EKF,UKF,粒子濾波等多種非線性濾波算法，發展了單模型以及SMM(static multiple model), IMM等多模型算法等。我國雖然跟蹤國外研究，積累了大量的基礎和經驗，部分理論研究處于國際領先水平，如周宏仁提出的“當前統計”模型，李曉榕提出的變結構多模型等理論，但總體上仍落后于國外發達國家。通過國內外的研究分析，可知國外在基礎研究和理論創新方面優勢較大，國內更多的研究是對國外所提理論的基本應用和改進。但是在機動目標彈道預報方面，國內外都鮮有文獻和資料，因此機動目標的彈道預報是一個較前沿的技術問題，加大對該方面研究將對搶占這方面的國際學術地位具有重要價值。

在多模型算法的實際應用上，國內外差距較為明顯。在美國，IMM算法已經在空中交通流量控制領域得到了很成功的應用。可以推測，該算法在軍事技術領域必定已經發揮了更大的作用。例如，預警機在對空中機動目標的跟蹤，特別是多目標跟蹤方面必定發揮了重要作用，只是未見詳細的公開報道而已。國內鮮有這方面的公開報道。

國外對彈道預測方法的研究僅限于彈道導彈方面，對機動目標預測方法的研究未見公開報道。而國內對彈道預測方法的研究也主要集中在彈道導彈方面，對機動目標彈道預測方法的研究較少，主要采用目標機動當前統計模型，沒有考慮目標的氣動力等復雜情況，利用Kalman預報原理向前簡單地推算。

[ 1] 陳玲，李少洪. 基于無源時差定位系統的機動目標跟蹤算法[J]. 系統工程與電子技術，2005, 27(1): 127-130. CHEN Ling, LI Shao-hong. Algorithm of Maneuvering Target Tracking with TDOA Passive Location System[J]. Systems Engineering and Electronics, 2005, 27(1): 127-130.

[ 2] 楊麗娜，袁鑄，閻保定，等. CS模型下的IMM算法在目標跟蹤中的應用[J]. 計算機工程與應用，2010，46(33)：230-232. YANG Li-na，YUAN Zhu，YAN Bao-ding, et al. Application of IMM Algorithm Based on Model CS in Target Tracking [J]. Computer Engineering and Applications，2010，46(33)：230-232.

[ 3] LI Xiao-rong,JILKOV V P. A Survey of Maneuvering Target Tracking Part I: Dynamic Models[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(4): 1333-1364.

[ 4] MOOSE R L,WANG P L. An Adaptive Estimator with Learning for a Plant Containing Semi-Markov Switching Parameters[C]∥IEEE Transactions on Systems,Man,Cybernetics,SMC-3(May 1973)：277-281.

[ 5] MEHROTRA K., MAHAPATRA PRAVAS R. A Jerk Model for Tracking Highly Maneuvering Targets[C]∥ IEEE Transactions on Aerospace and Electronics,1997:1094-1105.

[ 6] SINGER R A. Estimating Optimal Tracking Filter Performance for Manned Maneuvering Targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 1970, 6(4):473-483.

[ 7] SPALL J C.A One Measurement Form of Simultaneous Perturbation Stochastic Approximation[J]. Automatica, 1997, 33(1): 109-112.

[ 8] SADEGH P. Constrained Optimization via Stochastic Approximation with a Simultaneous Perturbation Gradient Approximation[J]. Automatica, 1997, 33(5): 889-892.

[ 9] 黨建武，黃建國.機動目標自適應高斯模型與跟蹤算法[J].電訊技術，2003,43(2)：109-113. DANG Jian-wu, HUANG Jian-guo. An Adaptive Gauss Model and Tracking Algorithm for Maneuvering Target[J]. Telecommunication Engineering，2003,43(2)：109-113.

[10] BAR-SHALOM Y.跟蹤和數據互聯[M].張蘭秀，趙連芳,譯.連云港：中船總七一六所，1991. BAR-SHALOM Y, Tracking and Data Association[M].ZHANG Lan-xiu, ZHAO Lian-fang, Translated. Lianyungang: CSIC 716 Institute,1991.

[11] 陳佳俊 , 劉高峰 , 辛晉生,等.機動頻率模糊自適應目標跟蹤算法研究[J].彈箭與制導學報，2010，30(2)：259-262. CHEN Jia-jun, LIU Gao-feng, XIN Jin-sheng, et al. Research on Maneuvering Frequency Fuzzy Adaptive Target Tracking Algorithm[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2010，30(2)：259-262.

[12] 徐琦；蔡聰；王熠釗. 一種基于數據融合的機動目標跟蹤預測算法[J].系統仿真學報，2011，23(11)：2444-2448. XU Qi,CAI Cong,WANG Yi-zhao. Forecast Algorithm for Tracking Moving Targets Based on Data Fusion[J].Journal of System Simulation, 2011，23(11)：2444-2448.

[13] 李繼杰, 陶建蜂, 郭相科. 一種處理機動目標的自適應Kalman濾波算法[J]. 彈箭與制導學報，2006,26(2)：1008-1009. LI Ji-jie, TAO Jian-feng，GUO Xiang-ke. A Kind of Improved Algorithm of Kalman Filter Applied to Maneuvering Target Track[J].Journal of Projectiles,Rockets,Missiles and Guidance, 2006,26(2)：1008-1009.

[14] 沈正陽，陸軍，匡綱要. 機動目標跟蹤中的多模算法[J]. 電光與控制，2002，9(4)：11-15. SHEN Zheng-yang, LU Jun, KUANG Gang-yao. The Multiple Model Algorithm in Maneuvering Target Tracking[J]. Electronics Optics & Control, 2002，9(4)：11-15.

[15] MAGILL D T. Optimal Adaptive Estimation of Sampled Stochastic Processes[J]. IEEE Transactions on Automatic Control, 1965, 10(4): 434-439.

[16] MAZOR E, AVERBUCH A, BARSHALOM Y， et al. Interacting Multiple Model Methods in Target Tracking: A Survey[J]. IEEE Transactions on Aerospace and Electronic Systems, 1998, 34(1): 103-123.

[17] 陳里銘，陳喆，殷福亮，等. 基于中心差分卡爾曼-概率假設密度濾波的多目標跟蹤方法[J].控制與決策，2013，28(1)：37-42. CHEN Li-ming,CHEN Zhe,YIN Fu-liang,et al. Central Difference Kalman-Probability Hypothesis Density Filter for Multitarget Tracking [J]. Control and Decision, 2013，28(1)：37-42.

[18] 劉育浩,黃新生. 基于中心差分卡爾曼濾波的SINS初始對準研究[J].壓電與聲光，2009，31(2)：189-191. LIU Yu-hao, HUANG Xin-sheng. Study of SINS Alignment Based on Central Difference Kalman Filter[J]. Piezoelectrics & Acoustooptics, 2009，31(2)：189-191.

[19] 夏忠婷,汪圣利,武洋. 基于SRCDKF的交互式多模型算法[J].現代雷達，2010，32(2)：66-70. XIA Zhong-ting, WANG Sheng-li, WU Yang. Interacting Multiple Model Algorithm Based on Square-Root Central Difference Kalman Filter[J].Modern Radar, 2010，32(2)：66-70.

[20] 王秋平,陳娟,王顯利,等.光電跟蹤系統中兩步非線性濾波算法研究[J].系統仿真學報，2008，20(13)：3385-3392. WANG Qiu-ping，CHEN Juan，WANG Xian-li,et al. Research on Two-Step Nonlinear Filter for Electro-Optical Tracking System[J].Journal of System Simulation, 2008，20(13)：3385-3392.

Maneuver Models Tracking Filter of Nonballistic Near Space Targets

LI Jun-long, QIN Lei, XIE Xiao-ying

(Beijing Institute of Electronic System Engineering，Beijing 100854，China)

Recently, America has successfully tested several flight vehicles flying in near space with high speed and maneuverability which brings great security threat to other countries. The maneuvering target with high speed is hard to be tracked by ground defense systems. Traditional filtering algorithms obviously cannot give accurate state estimation for such targets. Obviously, it will be a key technology to design accurate filtering algorithm for tracking such nonballistic near space targets in the future air defense systems. Four typical nonballistic maneuver modes of near space targets are proposed, and then the modes are discussed from three aspects including tracking filter ways of different maneuver modes, tracking filter ways of unknown maneuver modes, tracking filter ways of a combination of variety of maneuver modes. In the end the nonballistic tracking filter question and solutions are expounded.

nonballistic; near space; maneuver mode; tracking filtering; prediction; ballistic trajectory

2016-01-25；

2016-05-09 基金項目：有 作者簡介：李君龍(1964-)，男，遼寧錦州人。研究員，博士后，主要研究方向為飛行器導航、制導與控制。

10.3969/j.issn.1009-086x.2017.01.018

TJ765.1; TN713

A

1009-086X(2017)-01-0099-08

通信地址：100854 北京市142信箱30分箱 E-mail：351879610@qq.com