Devaney定義下變換的拓撲和隨機性質的關系

賈諾,王濤

(哈爾濱師范大學數學科學學院,黑龍江 哈爾濱 150025)

Devaney定義下變換的拓撲和隨機性質的關系

賈諾,王濤

(哈爾濱師范大學數學科學學院,黑龍江 哈爾濱 150025)

利用拓撲和遍歷理論對Devaney混沌意義下變換的弱混合與拓撲混合、拓撲傳遞及初值敏感的關系進行了研究,改進了已有文獻的結論,證明了弱混合則初值敏感.

保測變換;弱混合;拓撲傳遞;初值敏感

1 引言

Devaney混沌定義是目前普遍流行的幾個混沌定義之一[1],它從拓撲的角度刻劃了混沌,給出了一維、高維甚至是Banach空間上的非線性迭代系統的精確的數學描述,并逐步用于對混沌動力系統的研究,如醫學、經濟學、通信、工程、信息處理和概率理論等等[26].

在研究混沌的三種常用方法中,基于Devaney混沌定義的微觀拓撲方法和基于遍歷理論的隨機方法受到了廣泛關注[7].許多學者利用拓撲方法揭示了混沌定義中變換滿足的三個條件之間的關系[810],與此同時,由于系統軌道行為具有混合、弱混合和傳遞等特征,以泛函分析和譜理論為工具研究變換的混合性質的隨機方法也引起了研究者的濃厚興趣[1114].近年來,為了建立拓撲和隨機方法間的聯系,不斷有學者致力于動力系統的拓撲和隨機性質間關系的研究.徐正杰等[15]研究了連通、緊致、光滑的黎曼流形上的光滑迭代映射的混合與初值敏感的關系,研究結果表明混合是拓撲傳遞和初值敏感的充分條件.Salim[16]證明了對定義了Borel概率測度的非平凡緊致度量空間上的連續動力系統,若映射拓撲混合則初值敏感,且驗證了拓撲混合弱于混合.在文獻[17]中,我們證明了若連續變換f弱混合且周期點稠密,則f初值敏感.

為了進一步展示動力系統的拓撲和隨機性質,本文從一個新的角度分別驗證了弱混合與拓撲混合、拓撲傳遞及初值敏感之間的關系.研究表明弱混合則意味著拓撲傳遞和初值敏感,減弱了文獻[15-16]中的定理條件,改進了相關結果.

2 預備知識

設M 為度量空間,d為定義在M上的距離,f:M→M為M到自身的連續映射,則拓撲動力系統可以描述為(M,f),其中M 代表系統的狀態集合,f用于刻劃系統的狀態演化.

定義 2.1[1]度量空間(M,d)上M 到自身的連續映射f在Devaney意義下是混沌的,當且僅當下面條件成立：

(i)f是拓撲傳遞的,即對于 M 中的每一對非空集合 U和 V,存在一個正整數 n,使得

(ii)f的周期點集在M 中稠密;

(iii)f初值敏感,即存在敏感正常數σ＞0,對每一x∈M 和它的開鄰域Nx,存在一個非負整數n,使得

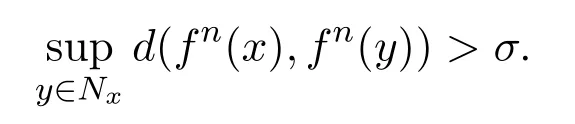
關于變換f:M→M 的其他相關定義如下：

(a)若對任意非空開集U,V?M,存在整數n≥0,使得對每個k≥n,都有

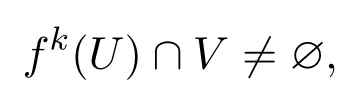
則f是拓撲混合的;

(b)若對任意可測集A∈σ(M)都有

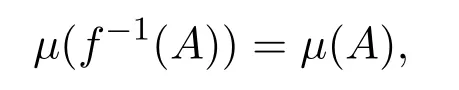
則稱f保持測度μ或測度μ是f不變的;

(c)若對任意A,B∈σ(M)有

則保測變換f:M→M 是弱混合的.

定義 2.2[11]設集合A??且n∈?.定義

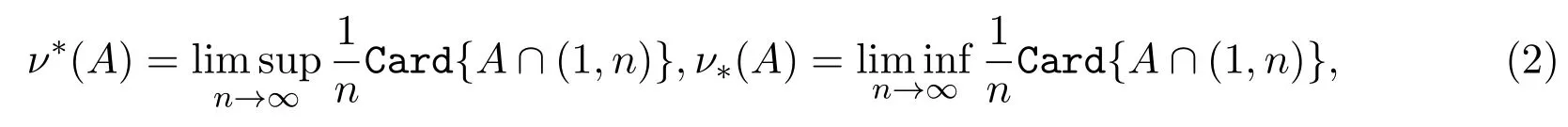
其中

表示大于1小于n的自然數集合,則ν?(A),ν?(A)分別稱為集合A的上密度和下密度.如果進一步有

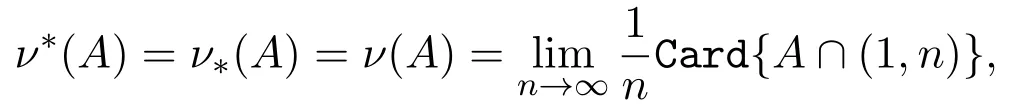
則稱ν(A)為集合A的密度.

3 主要結果

首先給出以下引理和定理的前提假設.設 (M,σ(M),d)是一個非退化的緊致度量空間, σ(M)表示(M,d)上的Borelσ-代數,μ為(M,σ(M))上的概率測度且其支撐集supp(μ)=M,即

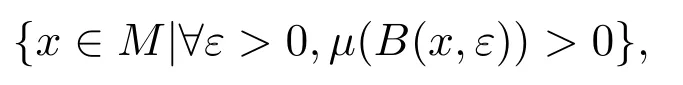
其中

f:M→M是M到自身的連續可逆保測變換.

引理3.1f:M→M 是弱混合的當且僅當對任意非空開集U,V?M,存在一個密度為1的正整數集K,使得對每一個k∈K,都有

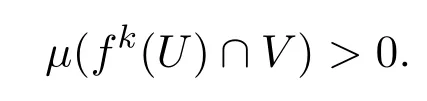
證明由文獻[18]中W 的性質可以直接得到結論.

命題 3.1若f拓撲混合則弱混合.

證明由f拓撲混合知,對任意非空開集U,V?M,存在非負整數N≥0,使得對每一個k≥N,有

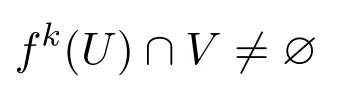
成立.于是,

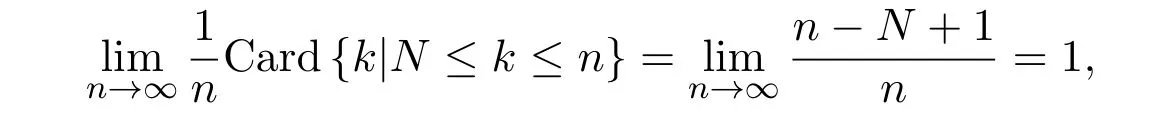
且

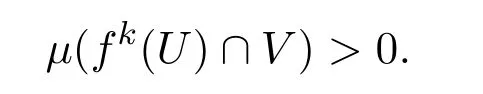
由引理3.1得f是弱混合的.

注 3.1在某些特定情形下,弱混合與拓撲混合是等價的,例如,f=a·A是緊致度量的Abelian群G上的仿射變換,其中a∈G,A:G→G是G上的滿同態.但通常由f弱混合無法得到拓撲混合,即命題3.1的逆命題未必成立.例如,在文獻[12]中,令τ(M)代表M 上所有保測變換全體構成的集合,若采用文獻[19]中的弱拓撲將τ(M)拓撲化,則在此拓撲下存在弱混合但非拓撲混合的變換.

命題3.2若f:M→M 弱混合則拓撲傳遞.

證明用反證法.假設變換f不是拓撲傳遞的,則存在M 中的非空開集U和V,使得對所有n∈?都有

于是

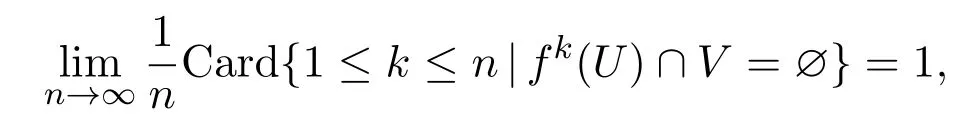
與引理3.1矛盾.因此f是拓撲傳遞的.

注 3.2這里我們基于引理3.1給出了命題3.2的證明,與文獻[17]中采用的遍歷定理方法不同,也更簡潔.

引理3.2若f:M→M 拓撲傳遞且支撐集supp(μ)=M,則對任意非空開集U?M,存在帶有正密度的非負整數遞增序列{nk}k≥1,使得

證明對任意M 中的非空開集U,由sup p(μ)=M 知μ(U)＞0.由于f保持測度μ,由不變測度的遍歷分解定理知存在遍歷測度ν,使得ν(U)＞0.根據Birkho ff遍歷定理,令

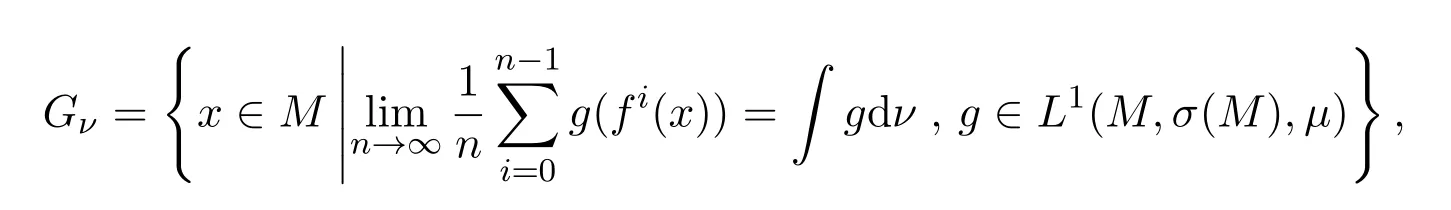
則ν(Gν)=1,因此且對任意x∈Gν∩U和g,有

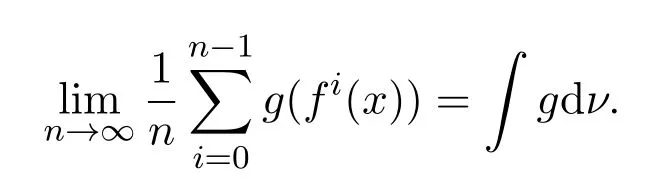
令

則

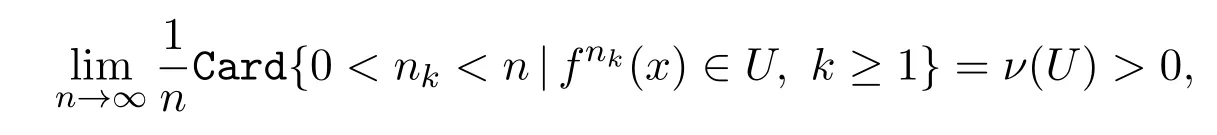
即

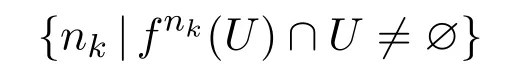
是帶有正密度的集合.

引理3.3設supp(μ)=M,f:M→M 是拓撲傳遞但非初值敏感的,則存在M 中的非空開集U,V和帶有正密度的非負整數遞增序列{nk}k≥1,使得

證明由M 是非退化的知,存在δ＞0,使得對任意y∈M 都有

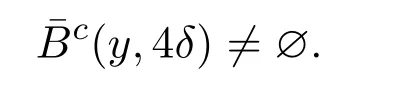
又由f不是初值敏感的可得,存在x∈M及其鄰域Nx,使得對任意自然數n≥0和y∈Nx有

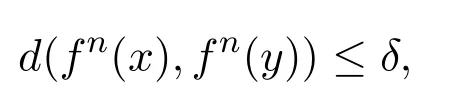
于是有

再由已知supp(μ)=M 得μ(Nx)＞0,根據引理3.2,存在帶有正密度的非負遞增整數整數序列,使得

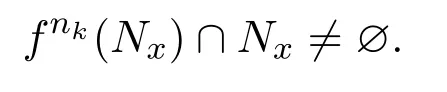
進一步,令

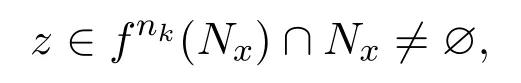
則存在ε＞0,使得B(z,ε)?Nx.于是對任意u∈B(z,ε)和所有k≥1,由不等式(6)得

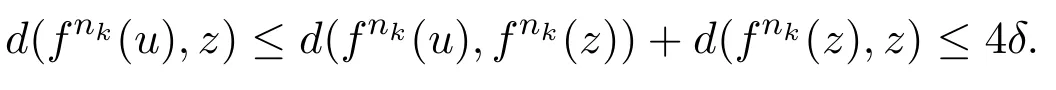
因此

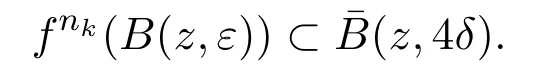
令

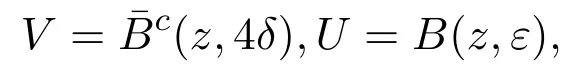
則V非空,且

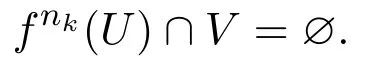
定理3.1若f:M→M 弱混合,supp(μ)=M,則f初值敏感.

證明由f弱混合及命題3.2知,f拓撲傳遞.若f不是初值敏感的,由引理3.3知,存在非空開集U,V?M 和帶正密度的非負整數遞增序列{nk}k≥1,使得

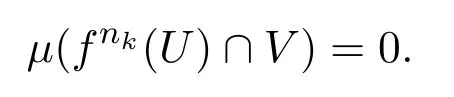
這與引理3.1矛盾.

4 結論

本文對Devaney混沌意義下變換f的拓撲和隨機性質的關系進行了探討,證明了若f是連續可逆保測變換,則f弱混合意味著拓撲傳遞和初值敏感.所得結論將文獻[15-16]的驗證條件減弱為弱混合,改進了其結論.在此基礎上仍有以下問題值得進一步研究：

(1)在一般流形上f拓撲傳遞并不能保證Devaney混沌定義中的其他兩條性質,是否一般流形下變換f的混合性質能保證其定義域內周期點的稠密性有待于進一步探討;

(2)本文中f的拓撲性質成立的充要條件;

(3)文獻[20-23]將f的隨機性質推廣到f的Zadeh延展型上.盡管已有一些文獻討論了的拓撲和隨機性質及與f的關系,但的拓撲和隨機性質的關系仍不清楚,需要進一步探討.

參考文獻

[1]Devaney R.An Introduction to Chaotic Dynamical Systems[M].Boston:Addison-Wesley,1989.

[2]Banasiak J,Lachowicz M,Moszynski M.Topological Chaos:When Topology Meets Medicine[J].Appl.Math.Lett.,2003,16(3):306-308.

[3]Khan M A,Mitra T.On topological chaos in the Robinson-Solow-Srinivasan model[J].Econom.Lett., 2005,88(1):127-133.

[4]Finn M D,Thi ff eault J L,Gouillart E.Topological chaos in spatially periodic mixers[J].Phys.D,2006,221(1): 92-100.

[5]Wei L,Ruan J.Chaotic dynamics of an integrate-and- fi re circuit with periodic pulse-train input[J].IEEE Trans.Circuits Syst.I,2003,50(5):686-778.

[6]Akhmet M U.Devaney’s chaos of a relay system[J].Commun.Nonlinear Sci.Numer.Simul.,2009,14(4):1486-1493.

[7]Rudnicki R.Chaos for some in fi nite-dimensional dynamical systems[J].Math.Methods Appl.Sci.,2004,27(6): 723-738.

[8]Banks J,Brooks J,Cairns G.et al.On Devaney’s de fi nition of chaos[J].Amer.Math.Monthly,1992,99(4):332-334.

[9]Vellekoop M,Bergllund R.On intervals,transitivity=chaos[J].Amer.Math.Monthly,1994,101(4):353-355.

[10]Syahida C D,Good C.On Devaney Chaos and Dense Periodic Points:Period 3 and Higher Implies Chaos[J].Amer.Math.Monthly,2015,122(8):773-780.

[11]Pollicott M,Yuri M.Dynamical Systems and Ergodic Theory[M].Cambridge:Cambridge University Press, 1998.

[12]Peter W.An Introduction to Ergodic Theory[M].Berlin:Springer,1981.

[13]Akin E.The General Topology of Dynamical Systems[M].Providence:American Mathematical Society, 1993.

[14]Grosse-Erdman K G,Manguillot A P.Linear Chaos[M].Berlin:Springer,2011.

[15]Xu Z J,Lin W,Ruan J.Decay of correlations implies chaos in the sense of Devaney[J].Chaos Solitons Fractals,2004,22(2):305-310.

[16]Salim L.On some stochastic properties in Devaney’s chaos[J].Chaos Solitons Fractals,2006,28(3):668-672.

[17]王濤,賈諾.Devaney混沌的隨機性質[J].數學的實踐與認識,2010,40(7):210-213.

[18]England J W,Martin N F B.On weak mixing metric automorphisms[J].Bull.Amer.Math.Soc.,1968,74(3):505-507.

[19]Halmos P R.Lectures on Ergodic Theory[M].Chelsea,New York,1956.

[20]Rom′an-Flores H,Chalco-Cano Y.Some chaotic properties of Zadeh’s extension[J].Chaos Solitons Fractals, 2008,35(3):452-459.

[21]Kupka J.On Devaney chaotic induced fuzzy and set-valued dynamical systems[J].Fuzzy Sets and Systems, 2011,177(1):34-44.

[22]Kupka J.On fuzzi fi cations of discrete dynamical systems[J].Inform.Sci.,2011,181(13):2858-2872.

[23]Lan Y,Li Q,Mu C,et al.Some chaotic properties of discrete fuzzy dynamical systems[J].Abstr.Appl.Anal.,2012,Article ID 875381,9 pages.

Links between topological and stochastic properties of transformation in definition of Devaney′s chaos

Jia Nuo,Wang Tao
(School of Mathematical Sciences,Harbin Normal University,Harbin 150025,China)

We explored the relationships between topological mixing and weak mixing,weak mixing and topological transitivity,weak mixing and sensitive dependence on initial conditions in the sense of Devaney’s chaos by using topology and ergodic theory.The main result that weak mixing can be seen as a new sufficient condition to sensitive dependence on initial conditions is obtained,which improves the results in existing literature.

measure-preserving transformation,weak mixing,topological transitivity, sensitive dependence on initial conditions

O193

A

1008-5513(2017)01-0012-07

10.3969/j.issn.1008-5513.2017.01.002

2016-11-23.

黑龍江省教育廳科學技術研究項目(12541243);哈爾濱師范大學青年學術骨干資助計劃研究項目(KGB201222).

賈諾(1978-),博士,副教授,研究方向：微分方程與控制論.

王濤(1977-),博士,副教授,研究方向:概率統計.

2010 MSC:37A25,54H20