基于穩健總體最小二乘的GPS水準擬合

趙全哲，徐愛功，徐宗秋，2，唐龍江

(1.遼寧工程技術大學 測繪與地理科學學院，遼寧 阜新 123000；2.武漢大學 衛星導航定位技術研究中心，湖北 武漢 430079)

基于穩健總體最小二乘的GPS水準擬合

趙全哲1，徐愛功1，徐宗秋1，2，唐龍江1

(1.遼寧工程技術大學 測繪與地理科學學院，遼寧 阜新 123000；2.武漢大學 衛星導航定位技術研究中心，湖北 武漢 430079)

針對GPS水準擬合中觀測數據存在粗差和系數矩陣存在誤差的問題，提出一種穩健總體最小二乘(RTLS)迭代算法。分析表明：與最小二乘(LS)相比，總體最小二乘(TLS)不僅考慮了自變量和因變量的誤差，同時也顧及了系數矩陣和觀測向量中存在的誤差；在利用TLS進行GPS水準擬合時，利用RTLS能較好地去除粗差，并合理地估計系數矩陣中含有誤差的部分。實驗結果證明利用RTLS水準擬合GPS的高程異常是最優選擇，且擬合的二次曲面效果最佳。

GPS水準擬合；高程異常；加權；RTLS；系數矩陣；觀測向量；粗差

0 引言

在利用最小二乘法(least squares，LS)估計未知參數時，通常默認觀測值不含系統誤差或粗差，所得參數解是最優無偏解。在實際參數估計過程中，誤差方程的系數矩陣(包括線性方程或經過泰勒展開的線性方程，如全球定位系統(global positioning system，GPS)觀測方程、變形位移方程等)本身就會包含誤差，這些誤差不僅與控制點的數量、觀測值類型和觀測網形有關，而且還與待定點的近似值等內容有關[2]。雖然LS是測量數據處理時最常用、最重要的方法，但該方法僅考慮了觀測誤差是偶然誤差的情況；而總體最小二乘(total least squares，TLS)在參數求解的過程中同時考慮了系數矩陣和觀測向量存在誤差的情況：因此它是顧及各種觀測量隨機誤差的一種最優算法[3]。國內外學者對TLS在測量領域的應用展開了一系列研究，包括直線擬合[4-5]、平面擬合[6]、水準測量[7]、坐標轉換[8]、地殼應變參數反演[9]等。

GPS水準擬合高程異常一般是通過建立多項式模型來求解擬合參數，該方法的基本思想是將平面坐標當作自變量，高程異常作因變量，采用抗差LS擬合多項式模型，這可以滿足目前大部分的工程需求。然而在精度要求較高的工程測量中，擬合模型的系數矩陣存在誤差的情況也需要考慮在內。因此，針對經典的高斯-馬爾科夫模型不能有效地應對系數矩陣中存在誤差的情況，本文嘗試采用一種新的穩健總體最小二乘迭代算法(robust total least squares，RTLS)擬合多項式函數，利用實驗數據分析LS與總體最小二乘奇異值法(singular value decomposition -total least squares，SVD-TLS)、混合最小二乘(mixed total least squares，MTLS)的差異性。

1 基于不同算法的總體最小二乘

1.1 總體最小二乘奇異值法

矩陣的奇異值分解是解決線性代數問題的工具之一，該分解法應用于統計學、矩陣的求逆、信號與圖像處理以及在誤差平差中的整體最小二乘、最小二乘、優化的問題中。誤差方程為

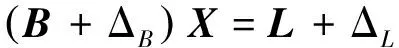
(1)

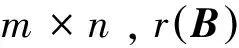
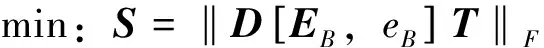
(2)

SVD-TLS通過分解增廣矩陣進而求解參數，能較好地處理病態矩陣，是求解TLS最常用、最嚴密有效的方法；不過缺少平差模型統計意義上的最佳估值，所以它的適用范圍具有一定的局限性。

1.2 混合總體最小二乘

在求解參數過程中，可以將LS和TLS混合使用，這種方法簡稱為混合整體最小二乘。誤差方程為

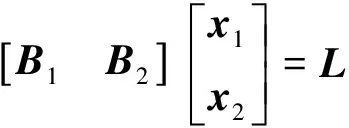
(3)

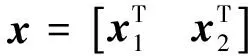
混合TLS矩陣分解法平差準則[11]為

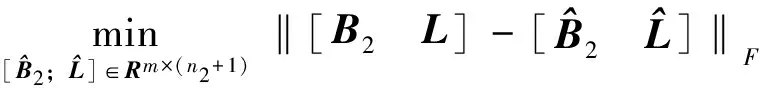
(4)

1.3 穩健總體最小二乘

SVD-TLS是從矩陣的特征值與零空間的角度出發擬合方程；而TLS迭代法一般是從測量平差角度出發，借助拉格朗日極值法并依據一定準則擬合方程。結合測量平差的優勢，文獻[12-13]根據線性回歸模型的特點推導出一種新的TLS迭代算法。設線性模型為

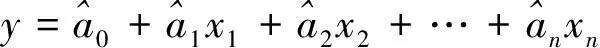
(5)

考慮到SVD-TLS系數矩陣中默認為不含誤差的列向量實際是含有誤差的，為了更方便地處理系數矩陣中含有誤差的部分，將式(5)變形為

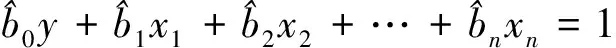
(6)

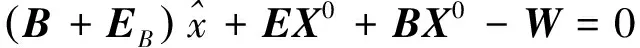
(7)

VTQ-1V=min。

(8)

式中Q是觀測值的協因數陣。根據拉格朗日極值求出線性回歸方程的TLS解為

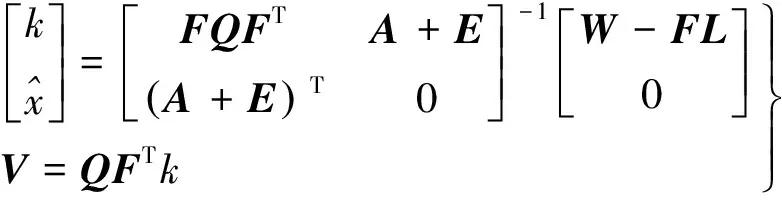
(9)

式中k為一組未知的常系數。

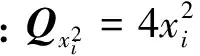
QB=Q0?Qy。

(10)

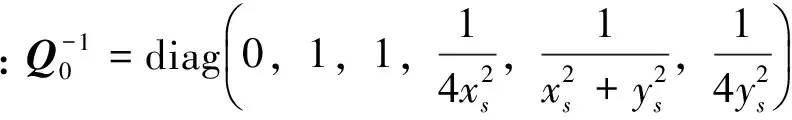
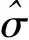
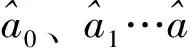
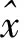
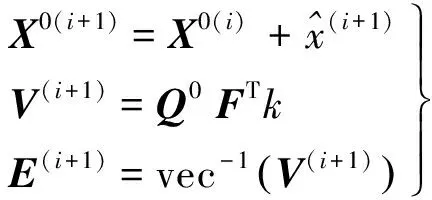
(12)

2 實驗與結果分析

2.1 直線擬合實驗

為分析上述3種TLS算法和LS擬合線性回歸方程的效果，利用文獻[18](其自變量和因變量都含有隨機誤差，不含粗差)提供的觀測數據，對選擇不同的自變量和因變量的直線方程y=ax+b、x=ay+b求解擬合方程，計算結果如表1所示。

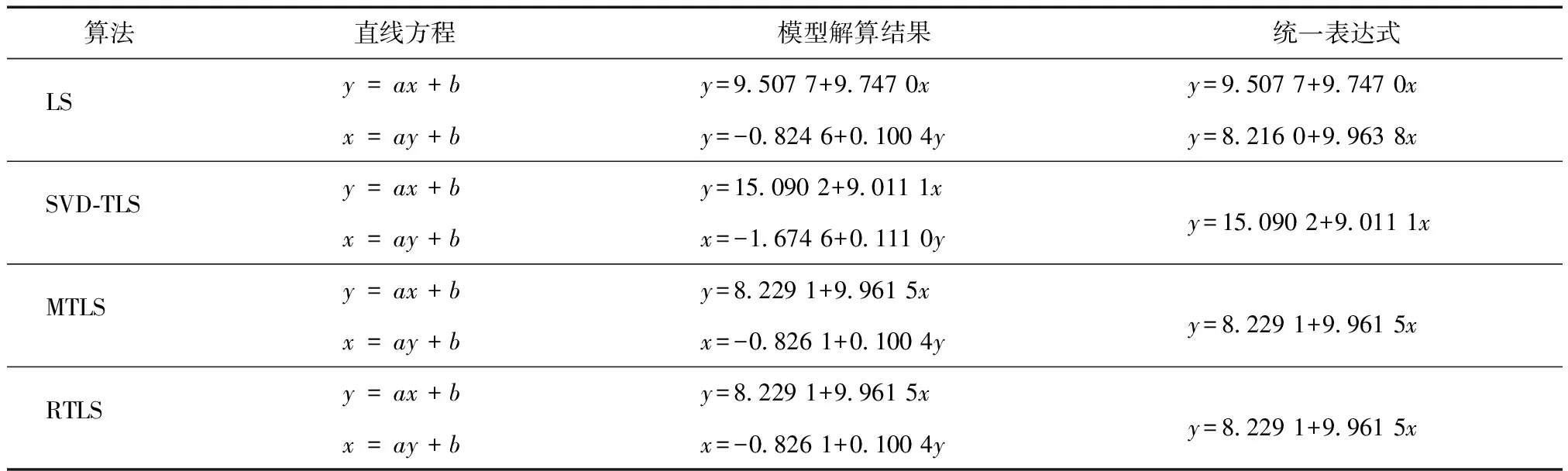
表1 幾種TLS算法求解參數結果

從表1可看出：交換自變量和因變量使得利用LS擬合出的結果不一致，而對利用TLS算法擬合的結果無影響，其中利用MTLS和RTLS擬合的表達式相同。這是因為LS沒有考慮自變量的誤差，只能保證一個方向上的最佳估值；而TLS擬合直線的實質為采用測點到擬合直線的正交距離的平方和最小的準則，并把自變量視為含有誤差的觀測量，這使得擬合的結果整體效果最佳，因此交換自變量對利用TLS擬合的直線無影響[19]。利用SVD-TLS與利用MTLS或RTLS擬合的直線方程不一致，這是因為：SVD-TLS雖然考慮了線性回歸模型中系數矩陣B的誤差，但是它們默認系數矩陣中不含誤差的常數列是含有誤差的；而MTLS和RTLS在考慮自變量誤差的同時又只顧及了平差模型中系數矩陣含誤差的部分。綜合分析來看，在利用TLS擬合直線時，應選擇擬合效果較好的MTLS或RTLS。

2.2 GPS水準擬合

為了分析TLS在GPS水準擬合中的效果，本文使用某市城區80組GPS聯測水準的高程數據，將其中的65組數據作為擬合數據，剩下的15組數據作為檢驗數據，如圖1所示。分別采用LS、SVD-TLS、MTLS、RTLS和抗差LS擬合一次曲面ζ=a0+a1x+a2y和二次曲面ζ=a0+a1x+a2y+a3xy+a4x2+a5y2，ζ為觀測向量。表2和表3分別列出了利用4種方法擬合一次曲面和二次曲面的系數及對應單位權中誤差。

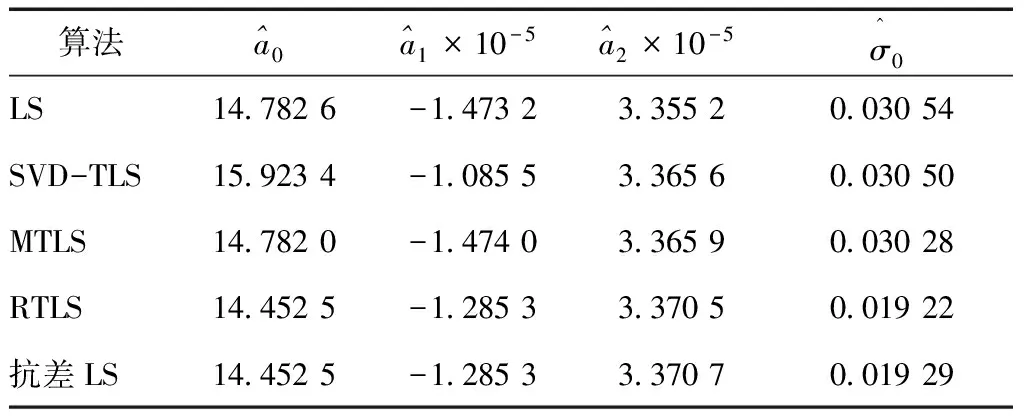
表2 一次曲面擬合結果及精度 m

從表2和表3列出的擬合系數可以看出，利用SVD-LS擬合曲面的系數與利用LS和MTLS擬合曲面的系數相差較大；利用RTLS擬合曲面的系數與利用LS、SVD-LS和MTLS擬合曲面的系數均不一致。從表2和表3列出的單位權中誤差可以看出，利用TLS擬合曲面的單位權中誤差優于LS，這是因為LS在曲面擬合中只考慮了觀測向量ζ的誤差，未顧及系數矩陣存在的誤差；利用MTLS擬合曲面的單位權中誤差優于LS和SVD-TLS，這是因為在利用MTLS擬合過程中合理地考慮了系數矩陣中含有誤差的列向量；利用RTLS擬合曲面的單位權中誤差明顯優于LS、SVD-TLS和MTLS，這是因為擬合數據存在粗差，RTLS能較好剔除粗差，并且合理地估計了系數矩陣中含有有誤差的部分。另外，與利用抗差LS擬合曲面的系數和單位權中誤差相比，利用MTLS擬合的結果與抗差LS擬合的結果近乎一致。

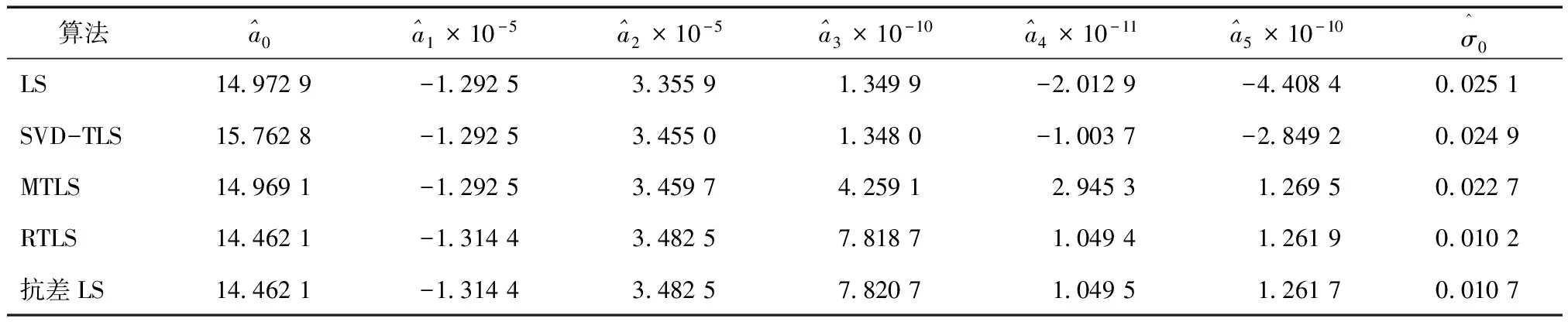
表3 二次曲面擬合結果及精度 m

圖2給出了分別利用MTLS和抗差LS擬合的一次曲面和二次曲面進行外部檢核的結果。從圖2可看出，利用抗差LS與RTLS擬合的曲面估計高程異常結果幾乎一致，并且利用2種方法得到的二次曲面的擬合效果優于利用一次曲面擬合的結果。值得注意的是，與抗差LS相比，雖然利用RTLS水準擬合高程異常的單位權中誤差精度沒有明顯提高，但RTLS對觀測向量和系數矩陣中含有誤差都進行了最小化約束；因此RTLS更適用于GPS高程異常的水準擬合。

3 結束語

為評價RTLS在GPS水準擬合中的應用效果，本文重點討論了SVD-TLS、MTLS和RTLS的平差準則以及測量處理模型，提出一種新的穩健總體最小二乘(RTLS)迭代算法應用于水準擬合。采用實測數據分析了LS與TLS的差異性，得出以下結論：

1)與LS相比，TLS同時顧及系數矩陣和觀測向量中存在的誤差，因此選擇不同的自變量仍能得到一致的結果；而LS只有在系數矩陣沒有誤差時，所求結果才是無偏的。值得注意的是，SVD-TLS默認系數矩陣中所有元素都含有誤差，而MTLS和RTLS僅考慮了系數矩陣存在誤差的部分。

2)在利用TLS進行GPS水準擬合時，利用RTLS擬合的結果優于利用SVD-TLS和MTLS擬合的結果。另外，利用RTLS水準擬合的高程異常的精度與利用抗差LS擬合的精度近乎一致，并且RTLS合理地估計了系數矩陣中含有誤差的部分，因此更適用于GPS水準擬合。

[1] 范東明.任意平面網坐標自動解算的非線性最小二乘平差算法[J].鐵道學報，2002，24(4)：78-82.

[2] 劉經南，曾文憲，徐培亮.整體最小二乘估計的研究進展[J].武漢大學學報·信息科學版，2013，38(5)：505-512.

[3] 孔建，姚宜斌，吳寒.整體最小二乘的迭代解法[J].武漢大學學報·信息科學版，2010，35(6)：711-714.

[4] SCHAFFRIN B，WIESER A.On weighted total least-squares adjustment for linear regression[J].Journal of Geodesy，2008，82(7)：415-421.

[5] 丁克良，沈云中，歐吉坤.整體最小二乘法直線擬合[J].遼寧工程技術大學學報：自然科學版，2010，29(1)：44-47.

[6] 魯鐵定，陶本藻，周世健.基于整體最小二乘法的線性回歸建模和解法[J].武漢大學學報·信息科學版，2008，33(5)：504-507.

[7] 楊仕平，范東明，龍玉春.整體最小二乘法平面坐標轉換在基坑水平位移監測中的應用[J].測繪與空間地理信息，2012，35(9)：221-223.

[8] 鄧罡.GPS高程擬合代替水準測量研究[D].長沙：中南大學，2012.

[9] 黃令勇，呂志平，任雅奇，等.多元總體最小二乘在三維坐標轉換中的應用[J].武漢大學學報·信息科學版，2014，39(7)：793-798.

[10]王樂洋，許才軍.總體最小二乘研究進展[J].武漢大學學報·信息科學版，2013，38(7)：850-856.

[11]魯鐵定，周世健，王樂洋.混合總體最小二乘的迭代解算算法[J].數據采集與處理，2015(4)：802-809.

[12]汪奇生，楊德宏，楊騰飛.線性回歸模型的穩健總體最小二乘解算[J].大地測量與地球動力學，2015，35(2)：239-242.

[13]魯鐵定，寧津生，周世健，等.最小二乘配置的QR分解解法[J].遼寧工程技術大學學報：自然科學版，2009，28(4)：550-553.

GPSlevelling based on robust total least squares

ZHAOQuanzhe1，XUAigong1，XUZongqiu1，2，TANGLongjiang1

(1.School of Geomatics，Liaoning Technical University，Fuxin，Liaoning 123000，China； 2.Research Center of GNSS，Wuhan University，Wuhan，Hubei 430079，China)

Aiming at the problem that there are errors in the observation data and the coefficient matrixes in GPS levelling，the paper proposed a robust total least squares (RTLS) algorithm.Analysis demonstrated that the TLS considered both errors of independent variables and dependent variables，and errors in the coefficient matrixes and the observation vectors，compared with LS；moreover，the GPS levelling with TLS could remove the errors easily and estimate the error parts in the coefficient matrixes reasonably by using the method of RTLS.Experimental result showed that RTLS would be the best choice for GPS levelling the height anomaly，and the effect of Quadric would be the best.

GPS levelling；height anomaly；weighting；RTLS；coefficient matrix；observation vector；error

2016-06-03

國家863計劃項目(2014AA121301)；國家青年基金項目(41504010)；遼寧省優秀人才計劃項目(LR201018)。

趙全哲(1990—)，男，遼寧沈陽人，碩士生，研究方向為高精度數據處理。

徐愛功(1963—)，男，山東日照人，博士，教授，博士生導師，研究方向為衛星定位與地理信息系統方面的理論與應用。

趙全哲，徐愛功，徐宗秋，等.基于穩健總體最小二乘的GPS水準擬合[J].導航定位學報，2017，5(1)：95-99.(ZHAO Quanzhe，XU Aigong，XU Zongqiu，et al.GPS levelling based on robust total least squares[J].Journal of Navigation and Positioning，2017，5(1)：95-99.)

10.16547/j.cnki.10-1096.20170120.

P228

A

2095-4999(2017)01-0095-05