貝葉斯網絡在用戶畫像構建中的研究

張小可　沈文明　杜翠鳳

摘要：為了解決用戶興趣變化動態推薦的問題，通過利用用戶的實時上網數據動態更新貝葉斯網絡各種興趣的概率，結合興趣閾值刻畫用戶畫像并實現移動應用的實時推薦。經過實驗表明，該算法能夠有效挖掘用戶的興趣，并具有較好的擴展性。

關鍵詞：用戶畫像 貝葉斯網絡 興趣閾值 動態推薦

1 引言

用戶畫像（Persona）最早是由交互設計之父Alan Cooper提出的，他認為用戶畫像是真實用戶的虛擬代表，是根據一系列用戶的真實數據而挖掘出的目標用戶模型[1]。通常用戶畫像是根據用戶的目標、行為、觀點的差異抽取用戶的典型特征，把用戶的基本屬性（年齡、性別、地域）、購買能力、行為特征、興趣愛好、心理特征、社交網絡大致地標簽化。

用戶畫像研究是當前的一個熱門話題，不少學者對移動互聯網、互聯網的數據構建用戶畫像，描述用戶的群體特征，從而為精準營銷提供數據支撐。曾鴻等通過對新浪微博數據進行采集分析，構建用戶畫像模型，描述企業用戶群體的行為特征，支撐精準營銷[1]；張慷通過提取用戶的上網行為特征，同時結合相關數據進行數據融合以及交叉分析，構建通信用戶的畫像模型[2]；黃文彬等在分析移動用戶的基站軌跡基礎上，采用頻繁模式挖掘、構建概率矩陣等方法，構建包含地理位置信息的用戶畫像模型[3]；王慶福采用貝葉斯網絡構建用戶興趣模型，以用戶興趣模型來刻畫用戶畫像[4]。在借鑒已有研究成果的基礎上，本文通過對移動互聯網用戶的歷史數據進行多元回歸分析，得到貝葉斯網絡的初始參數，再利用Netica軟件構造一個BN（Bayesian Networks，貝葉斯網絡）模型，并根據用戶實時發生的業務行為更新網絡的參數，以此刻畫每個用戶的畫像。

2 用戶畫像構建的相關研究

2.1 用戶畫像的定義

用戶畫像的本質就是消費者特征“可視化”。用戶畫像首先通過用戶一系列的行為信息進行用戶行為的初步“刻畫”；然后關聯用戶的動態行為數據進行畫像的完善，以此提高用戶需求偏好的準確度。本文先通過回歸分析歸納用戶的行為信息，再通過貝葉斯網絡關聯動態數據，更新用戶對需求的偏好概率。

2.2 用戶畫像構建思路

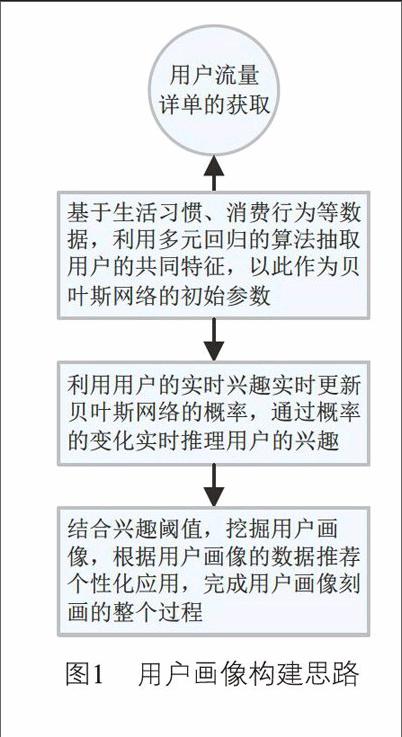
基于用戶畫像的定義，本文刻畫用戶畫像的步驟如圖1所示。

2.3 多元線性回歸模型

多元線性回歸模型是反映自變量與因變量之間“緊密性”的關系。因此，本文在分析用戶的生活習慣和消費行為的基礎上，采用多元線性回歸的方法來衡量用戶對某種移動應用的初始興趣度。

多元線性回歸模型：假設影響因變量Y的自變量個數為N，自變量記為x1， x2， …， xn，則自變量與因變量是線性關系：

Y=β0+β1x1+β2x2+…+βnxn+ε （1）

其中，β1， β2， …， βn是回歸系數；ε是與x1， x2， …， xn無關的未知參數，取值范圍為（0， σ2）。

2.4 貝葉斯網絡

眾所周知，用戶的興趣可能會受到身邊的朋友、同事或者家人的影響而發生改變。基于此，本文將通過貝葉斯網絡構建一種適應用戶興趣變化的動態推薦方法。

（1）貝葉斯定理

貝葉斯定理源于一個“逆向概率”的問題。如果袋子里有N個白球、M個黑球，則摸到黑球的“正向概率”容易得出；那么如果事前并不知道白球和黑球的比例，經過隨機摸出幾個球后，如何推測黑白球的比例呢？因此，貝葉斯的推斷不需要客觀的依據，它實際上需要一個估計值，然后根據實際的結果對估計值不斷修正。后來，Pierre Simona將貝葉斯的理論進一步發展為條件概率，幫助人們在概率相關的決策過程中，通過新獲得的觀察結果來更正對概率的判斷。在事件B出現的前提下，事件A出現的概率等于A和B都出現的概率除以B出現的概率，具體如下：

（2）

其中，P（A|B）是后驗概率；P（A）是先驗概率；P（B|A）/P（B）是一個調整因子，是在已知某些觀測所得到的結果。在預估先驗概率的前提下，再加入觀測結果，通過觀測結果來增強或者削弱先驗概率，由此得到更接近事實的后驗概率[5]。

（2）貝葉斯網絡

貝葉斯網絡是基于概率推理的圖形化概率網絡，是不確定知識表達與推理領域最有效的理論模型之一。它將經典的概率論與圖論結合起來，用于發現隨機變量之間的潛在關系，適用于表述和分析不確定的事件，可以從分散的、粗糙的信息中作出推理[6-7]。

假定有隨機變量組合X={X1， X2， …， Xn}，xi表示Xi的取值。表達式p（X1=x1， X2=x2， …， Xn=xn）表示一個聯合概率，即變量X1， X2， …， Xn的值分別是x1， x2， …， xn的概率。因此，給定一個隨機變量集合的完全聯合概率函數就能計算所有的邊緣概率和更低階的聯合概率[6]。為了更直觀表達聯合概率，用一個條件概率鏈表示聯合概率：

（3）

為了更直觀表達變量之間的聯合概率分布和條件的獨立性，后人用貝葉斯網絡來展現節點間相互依賴的關系，這種網絡表示的方法能夠大量地節約概率推理的計算。

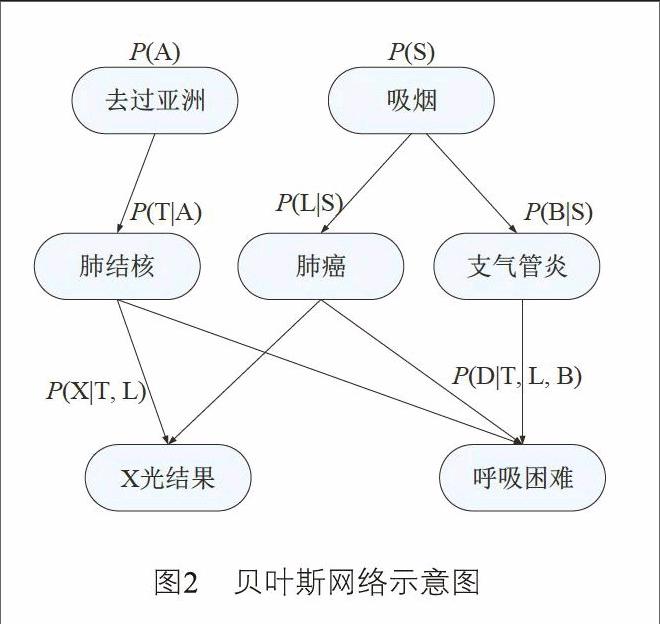
如圖2所示，一個貝葉斯網絡是一個DAG（Directed Acyclic Graph，有向無環圖），由代表變量節點及連接這些節點的有向邊構成[7]。

貝葉斯網絡用B（G， P）表示，圖2中的節點代表隨機變量，節點之間的有向邊反映節點之間的依賴關系。指向節點X的所有節點是X的父節點，T和L是節點X的父節點，表示T和L引起了X，T和L與X都存在因果關系，因此貝葉斯網絡有時叫做因果網[7]。貝葉斯網絡還蘊含獨立性假設，貝葉斯網絡規定圖中的任一節點Xi條件獨立于由Xi的父節點給定的非Xi后代節點構成的任何節點子集，即如果用A（Xi）表示非Xi后代節點構成的任何節點子集，用Πi表示變量Xi的父節點集，πi表示Πi的配置情況，πi表示某一具體的配置[8]。對于每個Xi將有一個子集Πi{X1， X2， …， Xi-1}，使得Xi與A（Xi）={X1， X2， …， Xi-1}＼Πi給定Πi的前提下是條件獨立的[7]。正如圖2所示，網絡中的節點T、L和X之間是一種收斂連接，在X光結果未知的條件下，T和L是相互獨立的；在警報X已知的情況下，T和L是相互依賴的，即不滿足：P（T， L|X）=P（T|X）P（L|X）。網絡中的節點S、L和B之間是一種發散連接，在節點S已知的條件下，L和B條件獨立，即滿足：P（L， B|S）=P（L|S）P（B|S）。節點L既是S和X順序連接路徑上的頭對頭型節點，則在已知節點L取值的條件下，X獨立于網絡中的節點S，即網絡模型得到的聯合概率為：

P（A， S， T， L， B， X， D）=P（A）P（S）P（T|A）P（L|S）

P（B|S）P（X|T， L）P（D|T， L， B） （4）

3 實驗過程

3.1 采用多元線性回歸計算用戶的初始興趣度

通過運營商的流量詳單記錄，選擇某地市100萬用戶的上網數據記錄，首先抽取用戶上網記錄的核心特征，然后根據公式（1）計算每個用戶的實時興趣度。通過對用戶上網應用的特征提取，歸納出9種代表性的應用：移動社交、手機游戲、手機電視、移動電子閱讀、移動定位服務、收集搜索、手機內容共享、移動支付、移動電子商務。

根據上面介紹的多元線性回歸方程，則某種應用的初始興趣度為：

Yi=β1Mi+β2Ti （5）

其中，Yi表示第i種商品的初始興趣度；Mi表示瀏覽網頁的次數；Ti表示瀏覽網頁的時間。通過公式（5）可以計算每個用戶對每種應用的初始興趣度，該興趣度可作為貝葉斯網絡中每種應用的初始興趣度。

3.2 構造用戶畫像的貝葉斯模型

把上述9種應用構造貝葉斯網絡，9個節點代表9種不同移動應用，節點間的有向弧代表用戶的初始興趣度，本文利用Netica軟件構造一個BN模型，某個用戶初始興趣的貝葉斯網絡如圖3所示。

3.3 利用實時興趣調整BN網絡中的概率

當獲得用戶的上網信息時，BN網絡中的概率就會自動更新。貝葉斯網絡最強大之處在于從每個階段結果所獲得的概率都是數學與科學的反映[9]。也就是說，假設了解用戶上網的足夠信息，根據這些信息獲得統計知識，網絡就會推斷合理的用戶興趣。當發現用戶使用移動支付時，則BN網絡的概率調整如圖4所示。

由圖4可知，當發現用戶使用移動支付后，用戶的可能使用定位服務的概率明顯提升。同時，還發現用戶使用了移動社交的服務，那么用戶的BN網絡的概率調整如圖5所示。

由圖5可知，當用戶使用移動社交后，用戶的收集內容共享、定位服務的概率得到提升。運營商可以根據實時的用戶興趣不斷更新BN網絡的概率，當發現用戶對某種應用的概率大于δ時（δ為用戶對某種應用的興趣閾值），運營商可以對該用戶進行應用推薦。根據應用推薦后，再跟蹤用戶的使用程度，以此來動態調整用戶對某種應用的興趣閾值。

3.4 基于貝葉斯網絡挖掘的用戶畫像結果

表1為用戶A、用戶B和用戶C一周登錄手機APP后所使用的應用，根據用戶的登錄次數、逗留時間計算出他們的興趣度，得到不同的應用興趣集。

從實驗數據得到用戶的興趣閾值δ為0.638。在表1中，可以預測用戶A感興趣的應用為{移動社交，移動定位服務，手機內容共享，移動支付，移動電子商務}；用戶B感興趣的應用為{手機游戲，收集搜索，移動支付，移動電子商務}；用戶C感興趣的應用為{移動社交，手機游戲，移動電子閱讀，移動支付，移動電子商務}。根據這些數據挖掘的信息，運營商或者移動應用供應商就可以為不同的用戶提供網上的個性化信息服務和推薦用戶喜愛的移動應用，提高運營商和移動應用供應商的服務效率及利潤。

4 結束語

本文采用貝葉斯網絡對用戶上網數據進行實時更新，以便實現用戶應用的個性化推薦服務。它能夠使先驗知識和實時數據有機地結合，實時更新網絡中的概率，并通過較為直觀的概率關聯關系來挖掘用戶的興趣，為構建用戶畫像提供了有力的數據支撐。實驗表明，采用貝葉斯網絡刻畫實時的用戶畫像，能夠動態跟蹤用戶預測用戶的興趣愛好，為運營商和移動應用供應商提供個性化的應用推薦切實可行的方法。

參考文獻：

[1] 曾鴻，吳蘇倪. 基于微博的大數據用戶畫像與精準營銷[J]. 現代經濟信息， 2016（16）： 306-308.

[2] 張慷. 手機用戶畫像在大數據平臺的實現方案[J]. 信息通信， 2014（2）： 266-267.

[3] 黃文彬，徐山川，吳家輝，等. 移動用戶畫像構建研究[J]. 現代情報， 2016，36（10）： 54-61.

[4] 王慶福. 貝葉斯網絡在用戶興趣模型構建中的研究[J]. 無線互聯科技， 2016（12）： 101-102.

[5] 湯偉. Android應用程序框架安全機制研究及改進[D]. 寧波： 寧波大學， 2011.

[6] 葉加加，趙逢禹. 基于興趣預測和熱點分析的聯合推薦算法研究[J]. 軟件導刊， 2016，15（9）： 25-28.

[7] 李儉川，胡蔦慶，秦國軍，等. 貝葉斯網絡理論及其在設備故障診斷中的應用[J]. 中國機械工程， 2003，14（10）： 896-900.

[8] 李伯宇. 通用決策模型生成及推理系統的實現及研究[D]. 西安： 西安理工大學， 2004.

[9] 郭振興. 分布式網絡故障管理的監測站點部署技術研究[D]. 長沙： 湖南大學， 2011.

[10] 魏芳. 基于貝葉斯網絡的用戶興趣發現[D]. 西安： 西安建筑科技大學， 2007.

[11] Neil M， Fenton N， Forey S， et al. Using Bayesian belief networks to predict the Reliability of military vehicles[J]. Computing and Control Engineering Journal， 2001，12（1）： 11-20.

[12] 陳麗花. 基于貝葉斯網絡的網上用戶興趣預測分析[J]. 煤炭技術， 2010，9（6）： 163-165.

[13] 胡春玲，吳信東，胡學鋼，等. 基于貝葉斯網絡的頻繁模式興趣度計算及剪枝[J]. 軟件學報， 2011，22（12）： 2934-2950.★