數值計算結合試驗測定模態阻尼法

唐宇航， 陳志堅， 梅志遠， 孫建連

(1.海軍工程大學 艦船工程系，武漢 430033; 2.國網蚌埠供電公司，安徽 蚌埠 233000)

數值計算結合試驗測定模態阻尼法

唐宇航1， 陳志堅1， 梅志遠1， 孫建連2

(1.海軍工程大學 艦船工程系，武漢 430033; 2.國網蚌埠供電公司，安徽 蚌埠 233000)

任一種分布的激勵必將引起多個模態的響應，試驗中要激出單一模態振動是很難的，傳統阻尼比估算方法所采用的信號處理手段不能有效分離疊加模態，以致測試阻尼比往往誤差較大。從多自由度疊加法動響應分析入手，指出模態混疊現象是制約精確阻尼比測試的重要因素，在阻尼較大、剛度較低時模態更密集、疊加效應更顯著，提出通過數值計算進行模態截斷以實現“純模態”提取的方案，推導了共振激勵下試驗與數值仿真結果中頻響峰值譜線表達式，找出二者間的關系，用純模態計算結果修正測試阻尼比。通過對4塊不同板單元進行前8階試驗模態分析與數值計算參數修正，結合頻響函數驗證了修正阻尼比的數據可靠性，得出了不同結構、材料間阻尼比差異的部分規律。結果表明,模型試驗對復合材料板的阻尼比識別準確性要低于鋼板，其阻尼性能往往被低估且修正幅度較大，該方法為模態參數識別的進一步研究提供了思路。

數值計算；模態阻尼比識別；頻響曲線；模態截斷；模態疊加

阻尼參數作為一項重要的動力性能指標，對結構在共振區的響應影響十分顯著，目前其取值常依靠經驗，具有一定的局限性，對特殊結構的振動響應預報缺乏借鑒意義[1]。因此，阻尼參數的取值亦常需要通過試驗來測定，然而試驗條件的微小差異均可能會造成測量結果的巨大偏差。雖然國內外也制定了相關行業標準，但事實上并沒有成為科研和生產上嚴格執行的規范[2-3]。實際工程結構阻尼成分復雜，一般是由內部阻尼(材料)、結構阻尼以及流體阻尼綜合決定[4]，然而現有阻尼測試標準(如GB/T 18258—2000、GB/T 16406—1996、GB/T 13665—2007、GB/T 17809—1999)多是針對試件的材料阻尼測量，有扭擺法、彎曲振動法、懸臂梁共振法、復模量圖示法和相位法[5]等，按照已有標準得到的阻尼參數在工程中往往難以直接運用，因此在尋找優良的阻尼材料以實現減振降噪等效果的同時，探究可靠實用的阻尼測試方法也十分緊迫。

模態阻尼比是多自由度系統動力分析中模態疊加法求解響應問題的重要參數，現有的設備和不同的測試方法在識別該參數時存在不穩定的現象，時常得到差異巨大的模態阻尼比結果，其信號處理手段可依頻域和時域兩大類劃分[6]。

頻域下常通過對一組激振和拾振點間的頻響函數進行信號處理計算出各模態參數，方法主要包括峰值拾取法、導納圓法、整體多項式擬和法或復指數擬和法等。其中，前兩者為單自由度圖解法，適用于模態不密集、小阻尼結構；后兩者為多自由度解析法，適用于模態密集、大阻尼結構。峰值拾取法依賴于半功率法阻尼估算理論，陳奎孚等[7-9]對該理論精度和誤差進行了分析，認為離散譜線難以獲得精確的半功率點、窗阻尼影響以及數字信號處理手段上的差異等，均會導致阻尼估算的偏差達到幾倍甚至幾十倍，得到錯誤結論。導納圓法計算精度受圖解精度的限制，且無法避免因鄰近模態疊加所產生的誤差[10]。擬合解析法常用于處理多自由度系統，然而一般為得到密集模態的信息會增加測點數目，這一舉措在增大了計算量的同時，也易產生病態的轉換矩陣從而影響參數識別精度[11]。

時域下的參數識別主要有對數衰減法、自由衰減法、隨機減量法等，在進行多自由度模態分析時需使用窗函數對時域信號進行濾波處理，經典窗可以辨識一般結構的模態參數，但在分離低頻密集模態、疊加模態時精度較差，特別是位于頻響函數的兩端且很接近的模態[12-13]，文獻[14]基于WT(Wavelet Transformation)理論討論了時頻分辨率及端點效應問題，應用AWT(Analytic Wavelet Transformation)準確識別阻尼參數的前提是具備高精度的隨機減量信號。WANG等[15]研究了一種僅運用結構自由振動信息識別多階模態參數的方法，利用離散的時序信號將廣義特征值問題轉為一般特征值問題。陳茉莉等[16]從時域理論入手，對壓氣機葉片的自由振動高頻模態成分進行分析，在忽略部分振型分量后逐步從原始數據中“剔除”已識別模態成分，再利用時域衰減法依次計算出前8階模態阻尼比。黃方林等提出一種僅測量輸出點的時域響應信號，計算其與時間軸所圍面積關系確定阻尼比的方法，抗干擾能力強、精度高、結果穩定。

在試驗中激起多自由度系統的“純模態”幾乎是不可能的，任一激勵下的響應必將是多個模態響應的疊加，已有研究多是運用信號處理的方法試圖將疊加模態分離出來，難以避免理論上的缺陷或繁瑣的運算。本文提出了一種數值計算結合試驗測定模態阻尼比的方法，利用程序中關于模態截斷的PCL(Patran Command Language)語言進行指定階次響應分析，以分離疊加模態得到“純模態響應”，推導出試驗數據的頻響峰值與數值分離所得“純模態”頻響峰值譜線間的關系，對模態阻尼比進行識別和修正。在此基礎上結合潛艇外殼輻射噪聲的實際計算需求，完成了4塊不同厚度、材質的船體典型局部板單元前8階模態阻尼比計算。

1 試驗設計

1.1 試驗背景

潛艇在水下航行時，外殼振動所輻射出的噪聲是設計師們關注的重點，其振聲性能直接關系到潛艇航行的安全性和隱身性。由于板殼材質、厚度等在全船范圍內分布復雜，直接用經驗取值描述總體阻尼偏離實際且誤差較大，淡丹輝等[17]提出單元化的阻尼比法則在控制結構總體模態阻尼比方面更具優勢，可在對多階模態阻尼比精確控制的同時又能解決分布式阻尼的建模問題。因此為對潛艇輻射噪聲進行更加可靠的預報，在計算殼體表面振動響應前應了解其實際阻尼分布情況，有必要對船體典型板單元結構進行阻尼比測試。按照相關規范，在進行整船有限元建模時板殼網格尺寸常按一個縱骨或一個肋位間距(500 mm左右)小者劃分，且盡量接近正方形。本試驗以此為依據構造典型板單元阻尼比測試模型，如圖1所示。

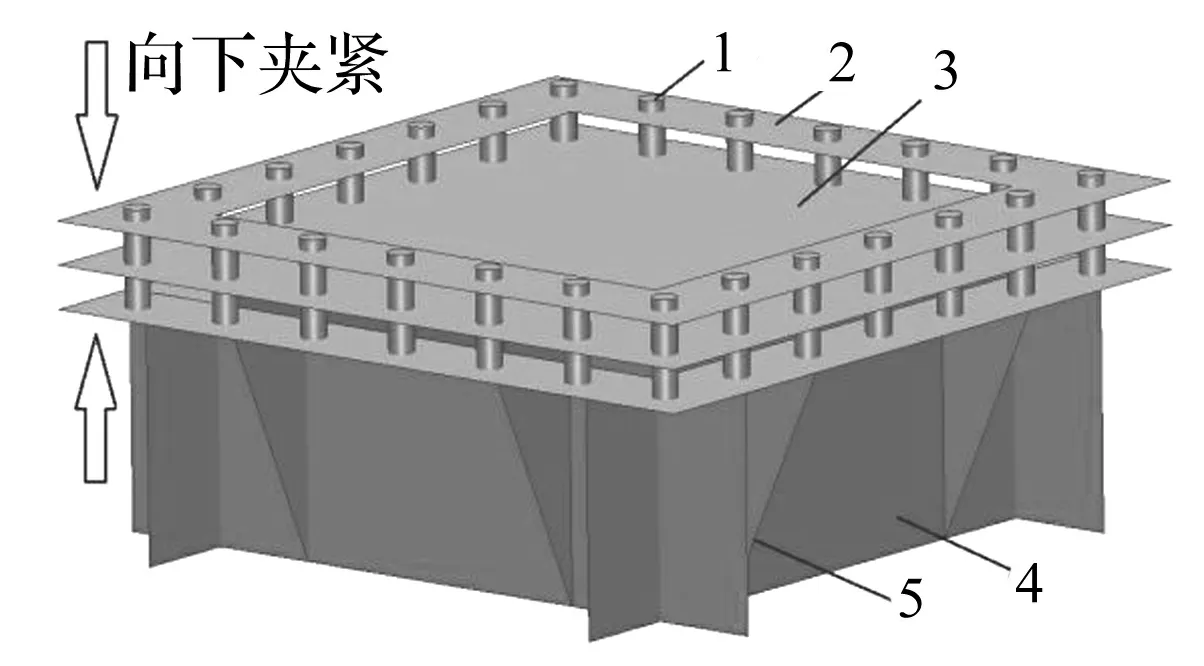
1-螺栓;2-壓條;3-板單元試件;4-基座;5-支撐加強結構圖1 試驗模型空間示意圖(測試內區域500 mm×500 mm)Fig.1 Experimental model spatial schematic diagram (test area 500 mm×500 mm)

1.2 試驗環境

試驗分別對500 mm×500 mm×3 mm規格Q235鋼板及與其等厚度、等剛度、等質量的3塊E800/350環氧樹脂材質的玻璃鋼板進行多階模態阻尼比識別。板單元模型尺度參數見表1。構造固定的邊界條件以模擬板在實船中與周圍肋骨等骨架的連接狀況，使用24根螺栓將板緊固在基座與壓條之間，注入玻璃膠填充縫隙以防止頻段內漏聲造成的誤差。為避免試驗激勵時板帶動基座產生耦合共振現象，基座使用15 mm厚度鋼塊焊制并在四周設置了支撐結構以增加其質量和剛度，控制其首階自振頻率在1 kHz以上，保證與各板單元前8階自振頻率有足夠的錯開率，試驗模型如圖1所示。

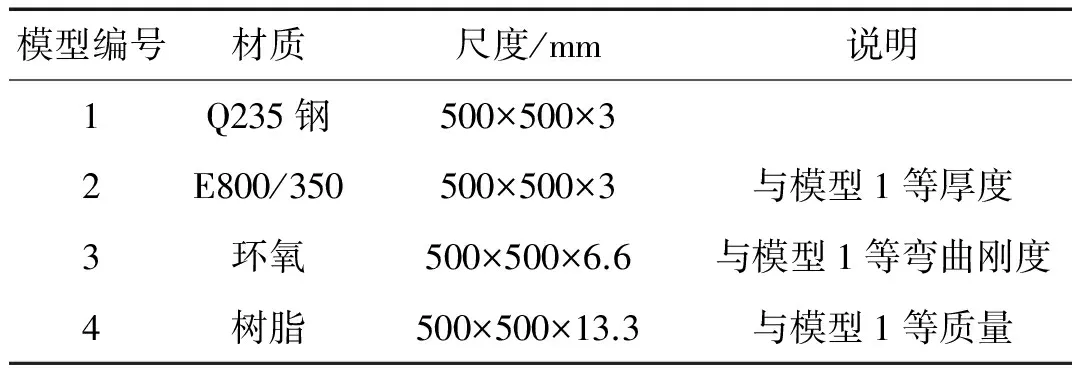
表1 板單元試驗模型尺度參數

試驗測試系統的構成如圖2所示。第1步采用多點激勵多點拾振的方法(以辨別對稱結構模態重根)進行模態測量，得到各階共振頻率和振型，力錘的脈沖激勵可以觸發結構寬頻帶自由振動，響應信號區分度高、識別清晰，板背面布置3個拾振點，正面依次敲擊81個激振點(見圖3)。第2步采用共振駐留法進行各階共振激勵，傳感器的布置根據事先進行的數值計算確定，既位于鄰近模態的“節點”、“節線”處，亦為各階振型下具有明顯響應的位置，在板背面布置9個測點(見圖4)。所有測點信號均用加速度傳感器采集。

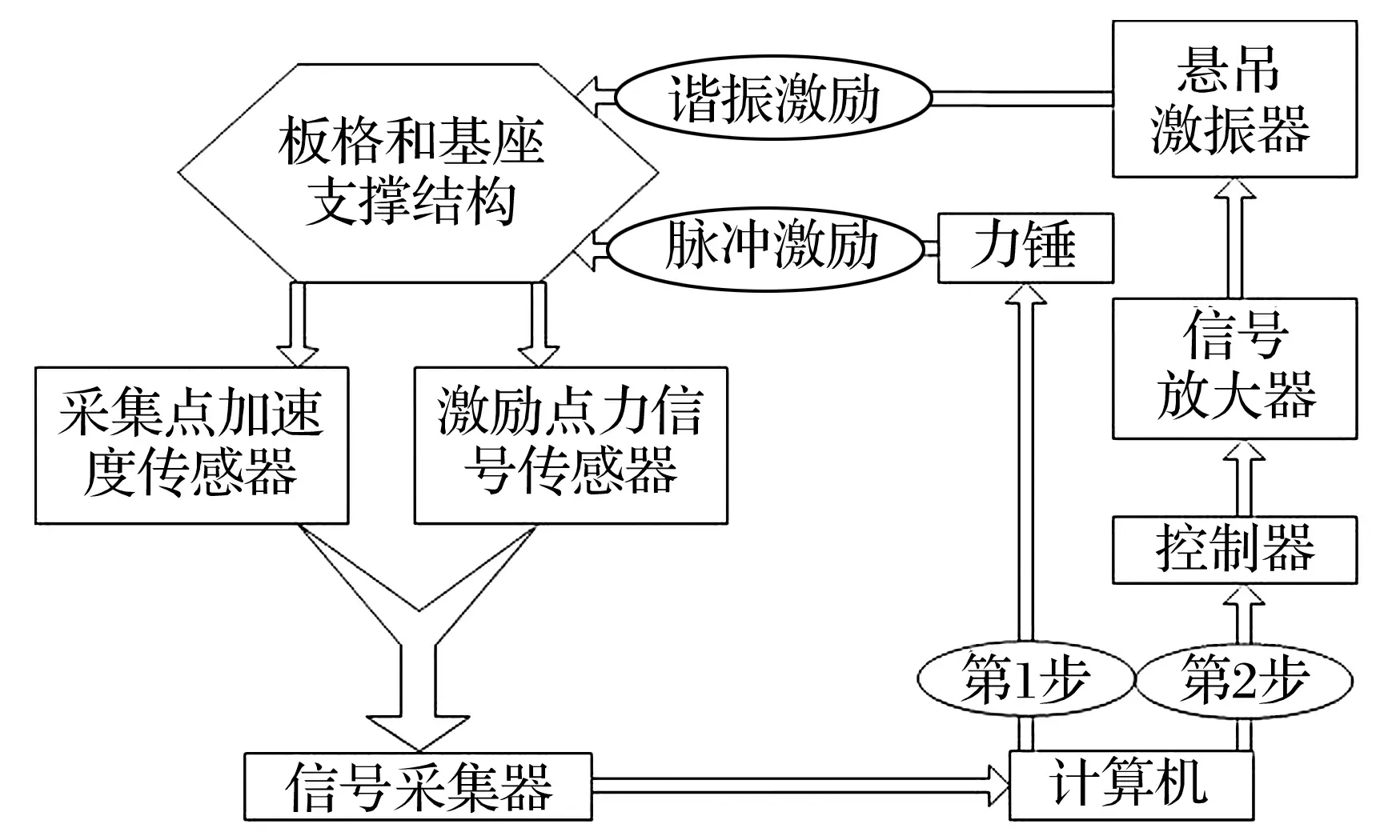
圖2 板單元模型測試系統的構成Fig.2 Experimental system constitution of plate element model

圖3 脈沖激勵試驗(模型1)Fig.3 Pulse excitation experiment (model 1)

圖4 共振激勵試驗(模型2)Fig.4 Resonance excitation experiment (model 2)

2 數值分析

2.1 有限元模型建立及模態分析

鋼材板與復合材料板的材料性能差異較大，試驗使用正交各向異性復合材料，計算時考慮纖維鋪層方向、角度和厚度等，其與鋼板相關參數在表2中給出。數值計算時對試驗模型進行整體有限元建模，模擬空氣中的振動情況，試件采用板單元、傳感器等集中質量用0Dmass單元進行模擬。諧振激勵試驗按各階振動響應明顯位置進行激勵和采集，數值仿真時按照與試驗模型上相對應的位置計算，并建立有限元模型。

數值計算時先對4塊板進行模態分析，得到前8階振型和固有頻率，各板振型相似，表3給出了各板單元試驗和仿真計算固有頻率對比以及模型2振型圖對比結果。由表3可見，試驗與數值計算的各對應階次振型基本一致；固有頻率結果存在小范圍相對偏差(<5%)，認為試驗模型與仿真模型匹配度高，頻率的相對誤差主要源于試驗中固定邊界不理想、人工網格劃分有誤差和集中質量分布不對稱等因素。對比鋼板與復合材料板可見，后者的部分階次計算相對誤差更大些，這是由于板材質的各向異性、生產工藝上偏差等因素對試驗結果產生了影響。

表2 玻璃鋼板與普通鋼板材料性能參數

Tab.2 Material performance parameters of glass fiber plate and common steel plate

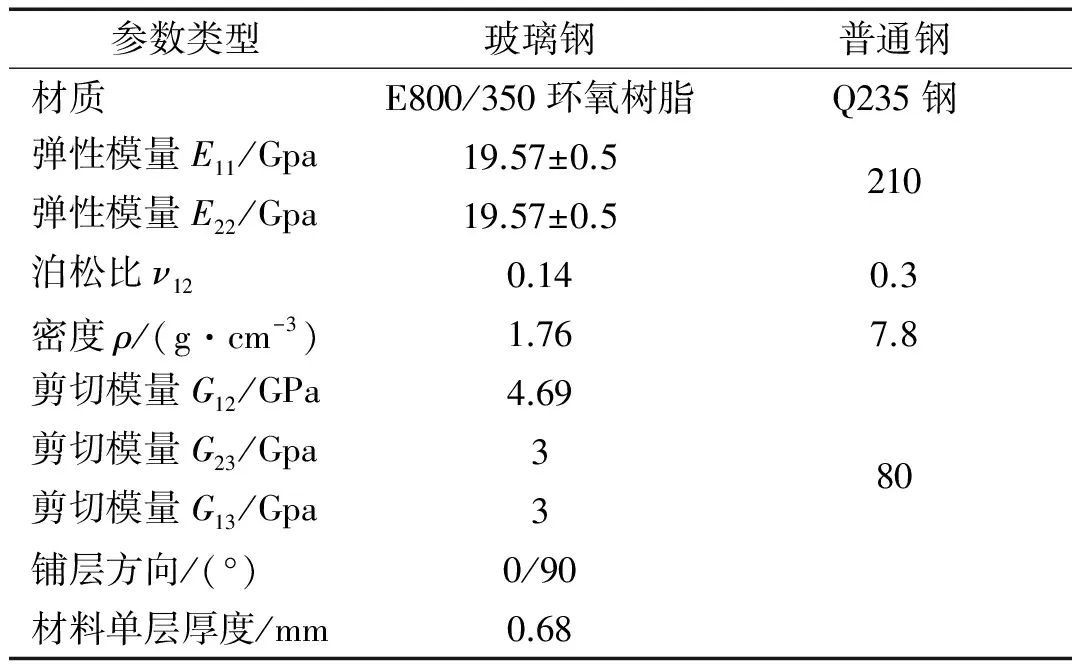
參數類型玻璃鋼普通鋼材質E800/350環氧樹脂Q235鋼彈性模量E11/Gpa19．57±0．5210彈性模量E22/Gpa19．57±0．5泊松比ν120．140．3密度ρ/(g·cm-3)1．767．8剪切模量G12/GPa4．69剪切模量G23/Gpa380剪切模量G13/Gpa3鋪層方向/(°)0/90材料單層厚度/mm0．68

2.2 共振激勵計算單一模態響應

對比各板單元試驗與數值計算的振型和固有頻率結果對應一致后，進行共振激勵計算。針對各階振型特點，按照與試驗中相對應的位置進行瞬態分析，及響應的頻域轉換。試驗中采集激振-拾振點時域信號后按力幅歸一化進行頻域轉化得到頻響函數，數值計算時施加單位共振激振力，激振、拾振點見表3。運用模態疊加法進行總響應分析前，采用Msc.Nastran中PCL語言的mode select語句對計算文件進行模態截斷，選擇關心的某階(或某幾階)模態進行響應計算。求解模態阻尼比時，精度較高的方法往往受單自由度理論的限制，這種模態選擇的方法可以在計算總響應前完成各模態分量的分離，精確地得到各階“純模態”下的結構響應，方便定向地研究指定階次的模態參數問題。

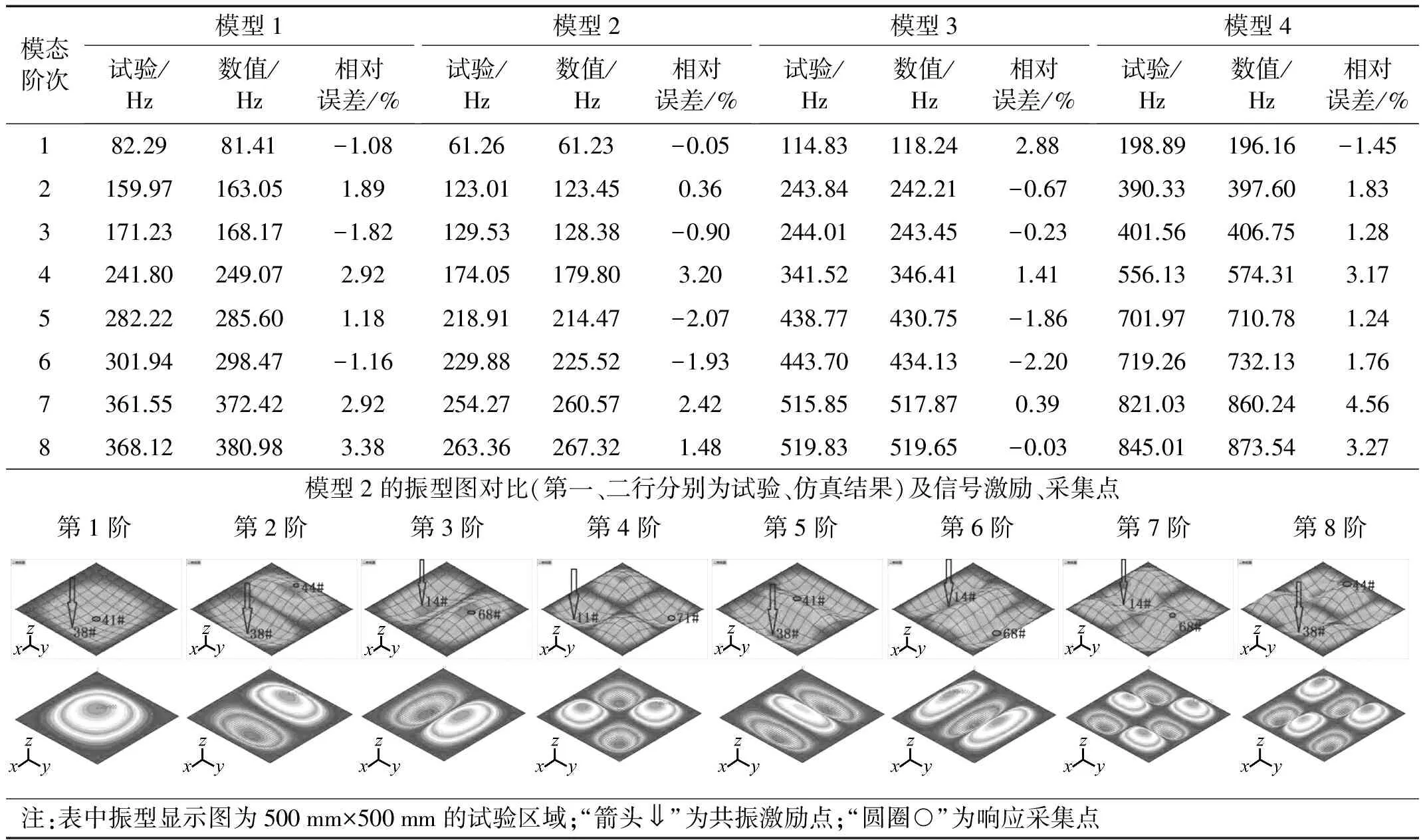
表3 4塊板單元模型前8階固有頻率的試驗與仿真對比結果

3 數據處理方法

3.1 模態混疊下阻尼比誤差分析

密集模態混疊原因有兩個:①各階模態的固有頻率靠的太近;②各階模態的阻尼比較大[18]。當出現以上情況時，則會在頻域上出現多個峰的相互疊加(見圖5)，直接運用傳統的阻尼估算方法就會帶來較大的誤差。文獻[19]在兼顧了頻率及阻尼比對模態混疊程度的影響下，按圖5對模態密集度進行了定義

(1)

將λ>1的模態視為密集模態，分析此時無法使用帶通濾波的時域法進行阻尼比計算。

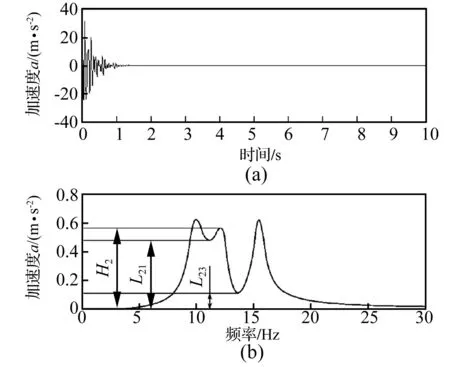
圖5 模態密集度的定義Fig.5 The definition of modesclosely degree

為明確模態混疊對傳統阻尼識別方法所產生的偏差影響，驗證“純模態”響應提取結果的可靠性。以模型4為例，設定其第4～8階模態阻尼比為0.007，并對該頻段進行數值仿真頻響分析，考察某一“激振-拾振”點間的頻響特性，用半功率法對該頻響反推模態阻尼比，同時將各階“純模態”頻響與總頻響進行對比，如圖6所示，計算結果見表4。從表4可見，第4階模態與其余階次混疊程度較輕(λ較小)，使用半功率法識別準確，對模態混疊嚴重的第7～8階模態，難以獲取正確的半功率點，誤差很大；從頻響曲線上看，總頻響中第4階附近曲線與該階“純模態”頻響高度一致，驗證了純模態計算準確可靠，受疊加影響，較高幾階頻響與純模態頻響差異較大。此外，由于各階振型間存在相位差，總頻響并不是各純模態頻響的直接疊加，對半功率帶寬的影響也存在差異，總之模態密集度越高(λ越大)，半功率法識別精度越差。

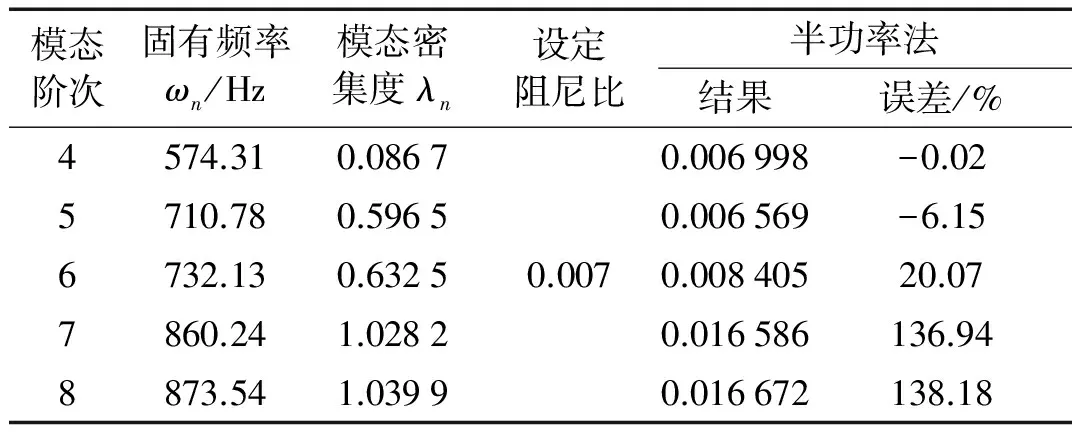
表4 半功率法估算密集模態阻尼比誤差分析

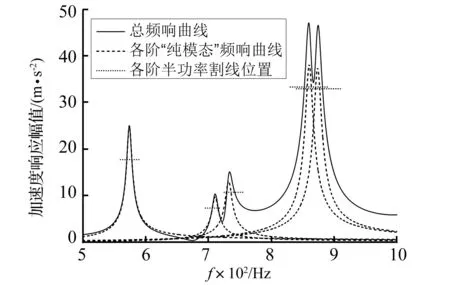
圖6 模型4第5～8階總頻響與純模態頻響對比(11#-71#)Fig.6 Comparison of total and pure mode frequency response during 5th to 8th frequency spectrum of model 4(11#-71#)

3.2 傅里葉變換下的傳遞函數

結構的動態特性可由N階矩陣微分方程描述

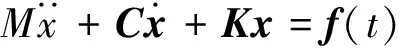
(2)

設系統的初始狀態為零，對式(2)兩邊進行拉普拉斯變換，可以得到以復數s為變量的方程

Z(s)X(s)=H(s)-1X(s)=F(s)

(3)

其中,

Z(s)=H(s)-1=[Ms2+Cs+K]

(4)

式中:Z(s)為廣義阻抗矩陣;H(s)為廣義導納矩陣，也就是傳遞函數矩陣。令s=jω，由式(3)得到頻域中輸出和輸入的關系

X(ω)=H(ω)F(ω)

(5)

式中,H(ω)為頻率響應函數矩陣，第i行第j列的元素(指僅在j坐標單位激勵下，i坐標頻響曲線)為

Hij(ω)=Xi(ω)/Fj(ω)

(6)

由式(4)得阻抗矩陣

Z(ω)=(K-ω2M)+jωC

(7)

令振型矩陣Φ=[φ1,φ2,…,φN]，則

(8)

因此，

(9)

式中:rHij(ω)為r階模態對Hij(ω)的貢獻;Yr為r階模態導納;mr、kr、cr和φr分別為第r階模態的質量、剛度、阻尼和振型;γr為激勵頻率與固有頻率之比;ζr為模態阻尼比。N自由度系統的頻率響應，等于N個單自由度系統頻率響應的線性疊加。

以上給出了任意頻響函數的疊加公式，可見任一點的頻響函數中均含有所有階次的模態響應成分，因此對于多自由度系統，想要激起單一模態響應是不實際的。測試系統頻響函數的獲取是基于能量的角度對線性系統的輸入與輸出進行頻域描述，即

Hxy(ω)=Gxy(ω)/Gxx(ω)

(10)

式中:Gxy(ω)為互譜，是對兩個周期信號在頻域上相關性的描述；Gxx(ω)為自譜(功率譜)，是對周期信號在頻域上的分布性描述。

其中，

(11)

(12)

對拾振點響應進行離散傅里葉變換(Q為傅里葉變換的點數)。即

(13)

將式(11)～式(13)代入式(9)

Hxy(ω)=Hxy(kΔω)=

(14)

測試系統同時測量了激勵、響應信號，按式(14)將時域信號通過傅里葉變換轉化成頻域上有限個點，得到各測點的頻響曲線。基于試驗所測信號所得的頻響曲線Hxy(ω)在理論上仍依賴于式(9)中的模態疊加規律。即

(15)

3.3 阻尼比修正方法

(16)

總響應為

小阻尼理論假設下，以低階共振頻率激勵時，系統響應主要來源于當前階的模態響應貢獻[20]。本文試驗對振型響應較顯著的位置進行激勵，拾振點布置在鄰近模態的“節點”或“節線”處，則響應中該階模態成分占比更高，因此式(17)可近似寫為

(18)

式中:rx(t)為r階模態的測點時歷響應;rxst為靜載荷p作用下測點位移。可見rx(t)時域最大值為rxst(1/2ζr)，將其代入式(13)進行頻域變換，得到r階固有頻率處所對應的頻率響應譜線表達式

(19)

(20)

根據式(19)～式(20)化簡得

(21)

試驗所得阻尼比是含有模態疊加影響因素的近似值，通過使用數值計算中模態選擇語句，實現僅對r階“純模態”進行響應計算，對比試驗與仿真在頻域下該階次共振頻率ωr處響應譜線峰值可完成阻尼比的修正。

4 測試數據及結果

4.1 共振駐留試驗響應分析對比

按照試驗順序分步使用力錘施加脈沖激勵、激振器施加諧振激勵，采集指定測點的加速度時序信號。①取3次力錘敲擊下激勵-響應點頻響曲線的平均值；②取激振器作用下形成穩態共振響應信號后一段時長(1.639 s)數據的頻響曲線結果并作3次平均，其中采樣頻率20 kHz，分析點數32 748，頻率分辨率0.61 Hz。模態初步分析時采用半功率法計算阻尼比，對該阻尼比初值利用“純模態”理論進行數值驗證，得到模型1～4各階振型下各共振激勵拾振點的加速響應，將其與試驗實測數據進行對比，如表5所示。可見，兩者所得共振峰值存在差異，由模態疊加導致的阻尼比估算誤差往往不可忽略。

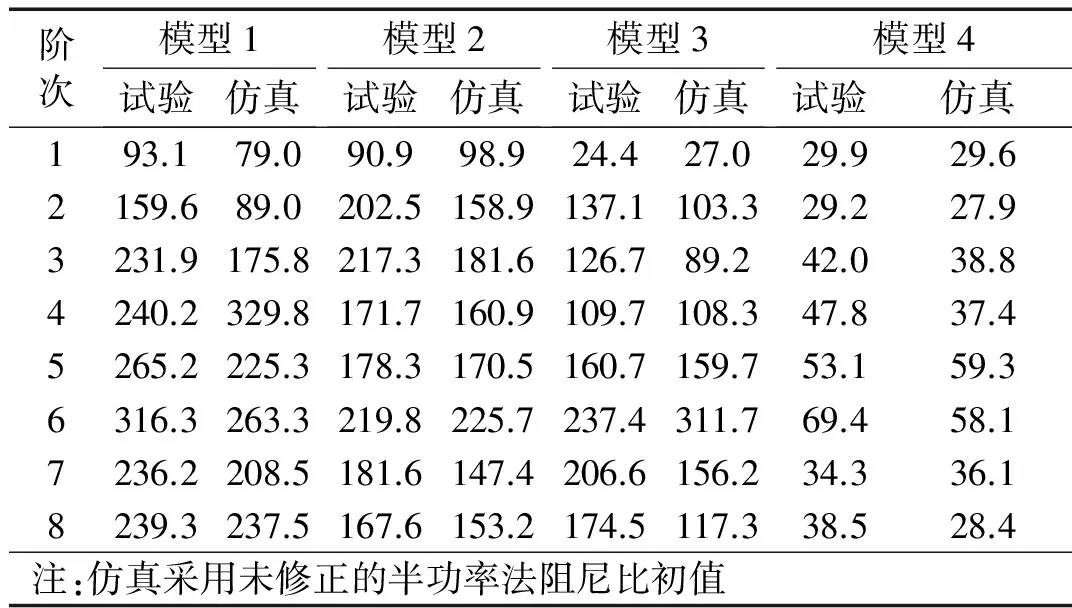
表5 模型1～4各階實測、按阻尼比初值仿真的加速度響應

表6給出了運用半功率帶寬法、帶通濾波衰減法所識別的模型1～4前8階模態阻尼比和修正后的阻尼比。可見，半功率法與衰減法識別出的阻尼比均存在一定偏差，衰減法偏差較大；由于模態混疊影響，頻域下的半功率帶寬較“純模態”計算下有偏差(大多變寬)，導致部分階次識別阻尼比偏大；從修正阻尼比來看，模型1～4，模型1(鋼板)阻尼較小，受模態混疊影響較小，半功率法可以獲得較為準確地結果，模型2～4(復合材料板)阻尼較大，模態混疊顯著，部分階次修正量較大。

圖7給出了模型1～4修正阻尼比對比結果。可見試驗中所用復合材料板的阻尼性能總體上大于鋼板，其各階模態阻尼比約為鋼板的4倍左右，即模型2～4各對應階次阻尼比相近，約為0.6%～0.9%，模型1約為0.2%～0.3%。因此在剛度滿足工程需求的條件下，設計時應充分發揮復合材料優良的阻尼性能來減振降噪。實際結構振動能量耗散由內部阻尼(材料)、結構阻尼(鉸鏈和界面處)和流體阻尼(流體-結構相互作用) 三部分阻尼機理所致。本試驗中所用薄板滿足二維平面假設，邊界條件及四邊約束下的板振型基本一致，模型1與模型2～4所表現出的阻尼比差異主要源于內部阻尼(材料內耗)；模型2～4的阻尼比差異則源于另兩類阻尼耗能，瑞利阻尼模型將非線性阻尼因素考慮在內，本質上以黏性阻尼理論對結構阻尼等進行等效以解耦運動方程，按該模型得出的阻尼比與頻率的關系[21]對玻璃鋼板試驗模型阻尼比結果進行數值擬合，如圖8所示。此外，模型1～4的首階阻尼比均大于各模型的其余階次阻尼比，主要由于一階振型為兩個方向半波疊加，造成面內剪切變形大，且該模態為強輻射模態，對介質輻射耗能大這兩方面因素所致。

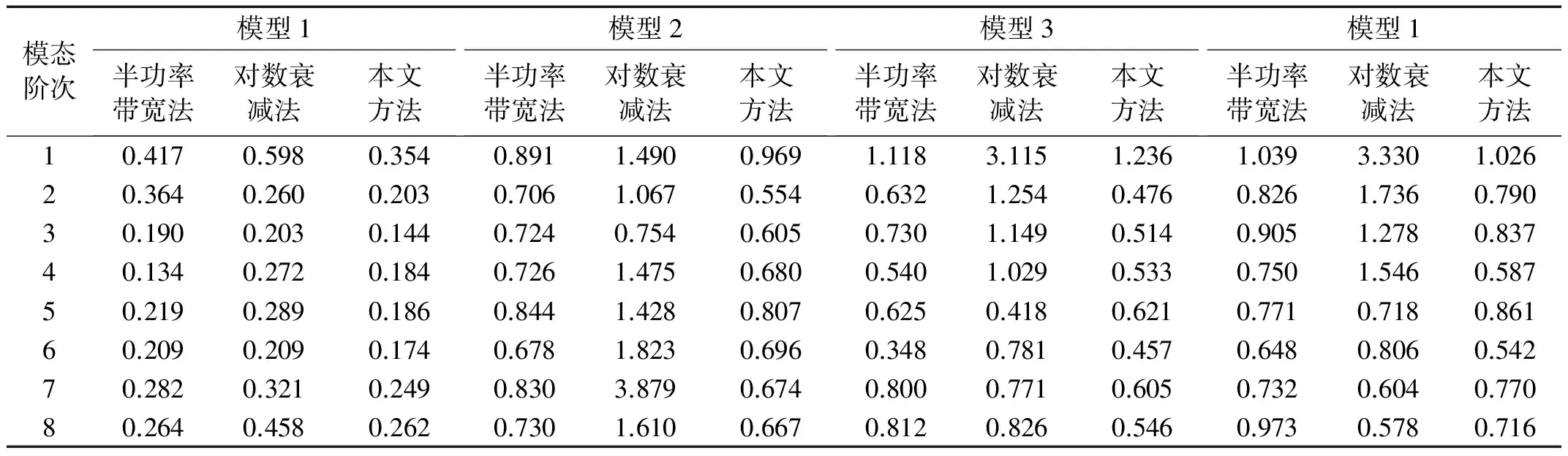
表6 4塊板單元模型前8階阻尼比修正結果與傳統方法計算結果對比

圖7 3塊板單元模型模態阻尼比理論修正值Fig.7 Theoretical correction values of 3 element model plates’ modal damping ratio

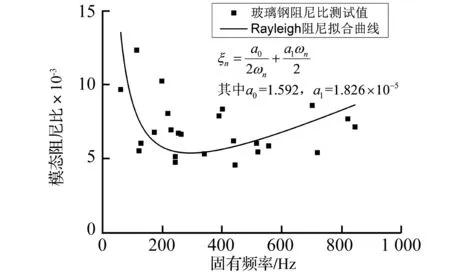
圖8 阻尼比與頻率的關系(Rayleigh阻尼)Fig.8 The relationship between damping ratio and frequency(Rayleigh damping)

4.2 寬頻帶激勵下阻尼比數值驗證

為驗證上述阻尼修正理論的可靠性，以11#(激勵)與71#(采集)測點間頻響函數為例， 結合4塊板脈

沖激勵試驗所得寬頻帶響應結果，與該頻段內數值計算(取修正后的阻尼比)頻響進行對比。4塊板的頻響曲線對比結果如圖9所示。

圖9中實線部分給出了按阻尼修正理論所得阻尼比數值計算出的頻響曲線，將該曲線與試驗數據對比可見，除因固有頻率微小差異導致的譜線峰值小幅偏移外，曲線在峰值大小、分布形狀上均與試驗結果高度匹配，可認為該理論所得阻尼比較可靠。較厚的模型4板在工藝上存在輕微缺陷，個別局部振動模態對頻響結果產生了一定影響，但其主振動頻響同樣符合規律。

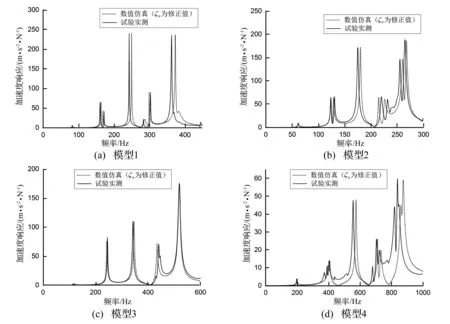
圖9 模型1～4寬頻帶頻響分析Fig.9 Broadband frequency response analysis of model No.1～4

5 結 論

目前系統模態阻尼比的獲取主要依賴于試驗，然而現有的測試方法、理論和軟件運用于實際工程結構時具有一定的局限性，難以得到精確的阻尼比結果。本文對常用信號處理方法的缺陷進行歸納，從經典模態分析方法入手，明確了響應中“模態混疊”難以分離的現象是造成阻尼比參數識別誤差的重要因素之一。另外，采用數值計算結合試驗的方法，利用Msc.Nastran中模態選擇語句進行模態截斷，計算“純模態響應”從而實現疊加模態的分離，按該方法結合試驗對4塊不同板單元前8階模態阻尼比進行識別與修正，并通過單位脈沖下寬頻帶頻響曲線的對比驗證了修正結果的可靠性。

此外，對于這種實際船體分析時常用的典型板單元結構，其阻尼性能有如下結論：

(1)相同邊界條件及結構振型下，薄板的材料是影響其模態阻尼比的主要因素，模型構件的剛度、質量分布特性對阻尼比的影響滿足瑞利阻尼模型規律。

(2)文中板單元模型各階模態阻尼比(鋼材)約為0.2%～0.3%，復合材料的阻尼性能要優越于鋼板，玻璃鋼(E800/350環氧樹脂)的阻尼比約為鋼板的4倍左右。由于復合材料結構的阻尼大，模態密集度高、疊加效應明顯，一般分析方法易于產生較大的識別誤差，更有必要對試驗估算的阻尼比進行修正。

因此，這種從數值計算實現疊加模態分離的角度來提高阻尼比測試精度的方法，有助于更準確地探究不同材料、結構的阻尼性能，為實際工程結構的模態參數識別理論發展提供了新思路。

[ 1 ] 郭雪蓮,范雨,李琳. 航空發動機葉片高頻模態阻尼的實驗測試方法[J]. 航空動力學報, 2014, 29(9): 2014-2112. GUO Xuelian, FAN Yu, LI Lin. Experimental test method for high-frequency modal damping of turbo machinery blades [J]. Journal of Aerospace Power, 2014, 29(9): 2014-2112.

[ 2 ] YIN F, OHSAWA Y, SATO A,et al. Characterization of the strain-amplitude and frequency dependent damping capacity in the M2052 alloy [J]. Materials Transactions, 2001, 42(3): 385-388.

[ 3 ] 鄭成琪,程曉農. 金屬阻尼性能測試方法的現狀與發展[J]. 實驗力學, 2004, 19(2): 248-256. ZHENG Chengqi, CHENG Xiaonong. Present status and future of damping measurement for metals[J]. Journal of Experimental Mechanics, 2004, 19(2): 248-256.

[ 4 ] SILVA C W.振動阻尼、控制和設計[M]. 北京:機械工業出版社,2013:8-9.

[ 5 ] 戴德沛.阻尼減振降噪技術[M].西安:西安交通大學出版社,1986:74-75.

[ 6 ] 黃方林,何旭輝，陳政清,等. 識別結構模態阻尼比的一種新方法[J]. 土木工程學報, 2002, 36(6): 20-23. HUANG Fanglin, HE Xuhui, CHEN Zhengqing, et al. A new approach for identification of modal damping ratios for structure [J]. China Civil Engineering Journal, 2002, 36(6): 20-23.

[ 7 ] 陳奎孚,焦群英. 半功率點法估計阻尼比的誤差分析[J]. 機械強度, 2002, 24(4): 510-514. CHEN Kuifu, JIAO Qunying. Influence of linear interpolation approximation to half power points on the damping estimation precision [J]. Journal of Mechanical Strength, 2002, 24(4): 510-514.

[ 8 ] 陳奎孚,張森文. 半功率點法估計阻尼的一種改進[J]. 振動工程學報, 2002, 15(2): 151-155. CHEN Kuifu, ZHANG Senwen. Improvement on the damping estimation by half power point method [J]. Journal of Vibration Engineering, 2002, 15(2): 151-155.

[ 9 ] 應懷樵,劉進明,沈松. 半功率帶寬法與INV阻尼計法求阻尼比的研究[J]. 噪聲與振動控制, 2006, 26(2): 4-6. YING Huaiqiao, LIU Jinming, SHEN Song. Half-power bandwidth method and INV damping ration solver study [J]. Noise and Vibration Control, 2006, 26(2): 4-6.

[10] BROWN D L, ALLEMANG R J, ZIMMERMAN R D,et al. Parameter estimation techniques for modal analysis [R]. Sae Paper,1979,88(2):299-305.

[11] 孟凡通. 基于模糊聚類的密集模態參數識別方法研究及實現[D]. 秦皇島: 燕山大學, 2012.

[12] 劉紹奎,韓增堯. 基于Gauss濾波和Hilbert變換的模態阻尼辨識方法[J]. 強度與環境, 2008, 35(1): 29-34. LIU Shaokui, HAN Zengyao. Modal damping parameters identification based on Gauss filter and Hilbert transform [J]. Structure and Environment Engineering, 2008, 35(1): 29-34.

[13] 尹幫輝,王敏慶,吳曉東. 結構振動阻尼測試的衰減法研究[J]. 振動與沖擊, 2014, 33(4): 100-106. YIN Banghui, WANG Minqing, WU Xiaodong. Decay method for measuring structural vibration damping [J]. Journal of Vibration and Shock, 2014, 33(4): 100-106.

[14] 申建紅,李春祥,李錦華. 基于解析小波變換識別結構的模態阻尼參數[J]. 振動與沖擊, 2009, 28(10): 89-93. SHEN Jianhong, LI Chunxiang, LI Jinhua. Identifying structural modal damping parameters based on analytic wavelet transformation [J]. Journal of Vibration and Shock, 2009, 28(10): 89-93.

[15] WANG B T CHENG D K. Modal analysis of mdof system by using free vibration response data only [J]. Journal of Sound and Vibration, 2008, 311(3/4/5): 737-755.

[16] 陳茉莉,李舜酩. 基于分布激勵突卸的轉子葉片阻尼比試驗[J]. 航空動力學報, 2009, 24(11): 2521-2526. CHEN Moli, LI Shunming. Damping ratio experiment study on rotary blade based on distributing excitation unloaded instantaneously [J]. Journal of Aerospace Power, 2009, 24(11): 2521-2526.

[17] 淡丹輝,孫利民. 結構動力有限元的模態阻尼比單元阻尼建模法[J]. 振動、測試與診斷, 2008, 28(2): 100-103. DAN Danhui, SUN Limin. Damping modeling and its evaluation based on dynamical analysis of engineering structure by finite element method [J]. Journal of Vibration, Measurement and Diagnosis, 2008, 28(2): 100-103.

[18] 李德葆,陸秋海. 實驗模態分析及其應用[M]. 北京: 科學出版社, 2001: 58-67.

[19] 黃應來,董大偉,閆兵. 密集模態分離及其參數識別方法研究[J].機械強度,2009,31(1):8-13. HUANG Yinglai, DONG Dawei, YAN Bing. Study on closely spaced modes decomposition and modal parameter identification[J]. Journal of Mechanical Strength, 2009, 31(1): 8-13.

[20] 溫金鵬,楊智春,李斌,等. 材料阻尼測試方法研究[J]. 振動、測試與診斷, 2008, 28(3): 220-224. WEN Jinpeng, YANG Zhichun, LI Bin, et al. A method for material damping measurement [J]. Journal of Vibration, Measurement and Diagnosis, 2008, 28(3): 220-224.

[21] 克拉夫R,彭津J. 結構動力學[M]. 北京:高等教育出版社,2006:184-185.

A method based on numeral calculation and experiment for determination of modal damping

TANGYuhang1，CHENZhijian1，MEIZhiyuan1，SUNJianlian2

(1.Department of Naval Architecture Engineering, Naval University of Engineering, Wuhan 430033, China; 2. State Grid Bengbu Power Supply Company, Bengbu 233000, China)

Any distribution of incentives lead to multiple modes of response, it is thus very difficult to stimulate single mode of vibration in experiments. The limitation of current signal processing techniques implies that traditional methods used to estimate the damping ratio cannot effectively separate the superposition modes, which leads to larger error in obtained damping ratio. Starting with modal superposition method theory in dealing with multiple-degrees-of-freedom system dynamic response, it was pointed out that mode confusion problem is one important limitation in precise damping ratio test. Modes are more crowded and the superimposed effect is more significant when system damping is larger and stiffness is lower. One program was proposed to achieve “pure mode” extraction by applying modal truncation in numeral calculation. The formula expressions of frequency-response spectrum peak line in both of resonance excitation experiment and numeral calculation were derived. The relationship between them was investigated. “Pure mode” calculation results were used to correct experimental damping ratio. Through four different board units, eight pre-order experimental modal analysis and numerical calculation parameter correction, combining frequency response function to verify data reliability of the correction damping ratio, some laws of damping ratio between different structures or materials were obtained. The results show that: the identification accuracy of composite plate’s modal damping ratio is lower than steel’s by model experiment calculation, and its damping performance is often underestimated and large amplitude correction are also often needed. The method provides a guideline for further study of modal parameter identification.

numeral calculation；modal damping ratio identification; frequency response curve; modal truncation; modal superposition

國家自然科學基金(51479205)

2016-04-19 修改稿收到日期：2016-07-20

唐宇航 男，博士，1991年生

陳志堅 男，教授，1957年生

TH212；TH213.3

A

10.13465/j.cnki.jvs.2017.04.006