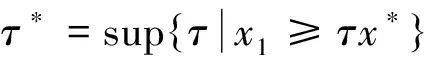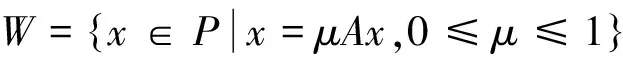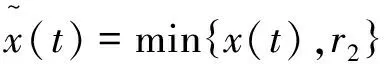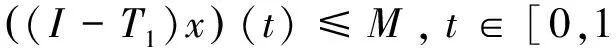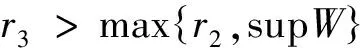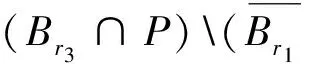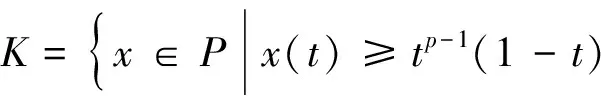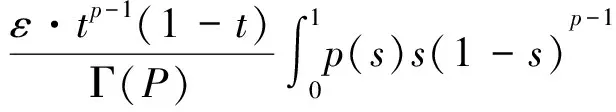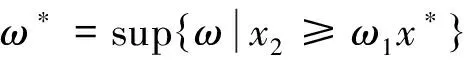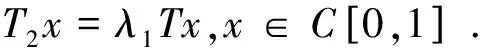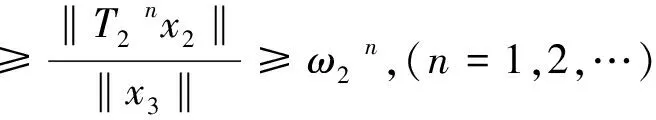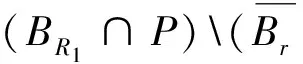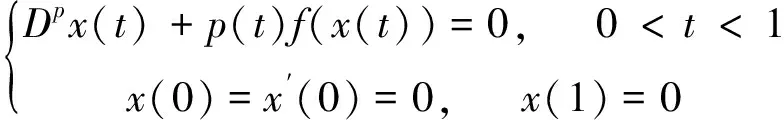分數(shù)階微分方程邊值問題的正解
趙 聰,魏帥帥
(1.山東科技大學 數(shù)學與系統(tǒng)科學學院, 山東 青島 266590;2.聊城大學 數(shù)學科學學院, 山東 聊城 252059)
分數(shù)階微分方程邊值問題的正解
趙 聰1,魏帥帥2
(1.山東科技大學 數(shù)學與系統(tǒng)科學學院, 山東 青島 266590;2.聊城大學 數(shù)學科學學院, 山東 聊城 252059)

正解;第一特征值;不動點指數(shù)
近年來,關于分數(shù)階微分方程邊值問題的解已經(jīng)被眾多學者研究[1-8]), 大多數(shù)研究證明了分數(shù)階微分方程解的存在性、 唯一性以及它們至少存在一個或多個正解. 例如,文獻[4]的作者討論了邊值問題
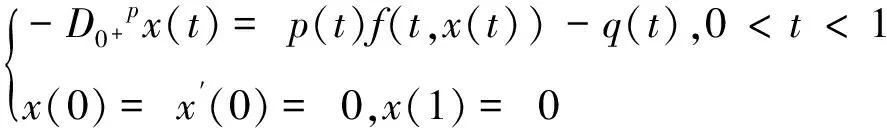
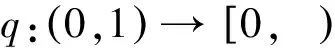
許多作者也通過運用不動點指數(shù)、 相應線性算子的第一特征值等理論對非線性微分方程的解進行了研究[9-17], 但將以上兩理論結合對解進行研究的方法并未應用于分數(shù)階微分方程. 受到以上文獻的啟發(fā), 本文將討論分數(shù)階微分方程邊值問題
(1)
至少存在一個正解, 其中2 本文假設以下條件成立: 為了得到本文的主要結果, 給出以下相關定義和引理. 式中n-1≤p 引理1[7]令a∈R,σ∈C(0,1)∩L(0,1)且2 G(t,s)= (2) (i)tp-1(1-t)s(1-s)p-1≤Γ(p)G(t,s)≤ (p-1)s(1-s)p-1,?t,s∈(0,1) (ii)tp-1(1-t)s(1-s)p-1≤Γ(p)G(t,s)≤ (p-1)tp-1(1-t) , ?t,s∈(0,1) 定義算子A,T:P→P如下: t,s∈(0,1),x∈E (3) t,s∈(0,1),x∈E (4) 類似于參考文獻[9]的引理3可得如下引理. 類似于參考文獻[13]可得以下引理. (5) (6) 證明 由(5)式可知: 存在r1>0使得 f(u)≥λ1u, ?0≤u≤r1 (7) 令x*為T對應于λ1的正特征函數(shù), 則x*=λ1Tx*. 對于任意的x∈?Br1∩P,根據(jù)(7)式有 (8) 不妨假設A在?Br1∩P上沒有不動點(否則結論已成立). 需要證明 x-Ax≠μx*, ?x∈?Br1∩P,μ≥0 第二,假新聞泛濫。隨著人工智能不斷成熟,在制造假新聞這一領域里,AI極有可能成為利益方最好的工具,而媒體正是利益方輸送信息最好的渠道。利用人工智能技術進行音視頻造假、機器人水軍生產(chǎn)大量虛假新聞和評論等等,已形成一個“灰色產(chǎn)業(yè)鏈”,其推動力便是對利益和權力的追求。這一現(xiàn)象在 2016 年美國大選中就有所顯現(xiàn),各種假新聞對總統(tǒng)選舉產(chǎn)生了巨大影響,時至今日“通俄門”事件仍在美國發(fā)酵。由此發(fā)展,AI在未來新聞業(yè)的融合極有可能造成假新聞泛濫的局面,這說明未來新聞業(yè)的發(fā)展或許很大一部分是數(shù)據(jù)權利的博弈。在這場博弈中,人們看到的世界是真實的世界嗎?無疑,新聞的真實性會受到嚴重的沖擊與挑戰(zhàn)。 (9) (反證法): 假設存在x1∈?Br1∩P以及τ0≥0使得x1-Ax1=τ0x*,那么τ0>0且x1=Ax1+τ0x*≥τ0x*.設 (10) 容易看出τ*≥τ0>0且x1≥τ*x*. 根據(jù)T(P)?P有 λ1Tx1≥τ*λ1Tx*=τ*x* 因此,由(8)式可得 x1=Ax1+τ0x*≥λ1Tx1+τ0x*≥ τ*x*+τ0x* 這與τ*的定義相矛盾, 故(9)式成立, 由引理5可得 (11) 根據(jù)(6)式可知, 存在0<η<1以及r2>r1, 使得 f(u)≤ηλ1u, ?u≥r2 (12) (13) 易知M<+. 令 (14) 下面證明W有界. ∫F(x)G(t,s)p(s)f(x(s))ds+ ∫[0,1]F(x)G(t,s)p(s)f(x(s))ds≤ (T1x)(t)+M,t,s∈(0,1) (15) (I-T1)-1=I+T1+T12+…+T1n+… (16) 根據(jù)T1(P)?P,有(I-T1)-1(P)?P. 因此我們得到x(t)≤(I-T1)-1M,t∈[0,1]. 且W有界. (17) 根據(jù)(11)式和(17)式可得 (18) (19) 式中λ1為(3)式中定義的T算子的第一特征值, 那么邊值問題(1)至少存在一個正解. 證明 設 那么由引理2的(i)可證得A,T:P→K. 令x*為T對應于λ1的正特征函數(shù), 則x*=λ1Tx*. 從而x*∈K. 根據(jù)(18)式可知,當u充分大時, 存在ε>0以及R1>0使得 f(u)≥(λ1+ε)u, ?u∈[R1,+) (20) 那么存在m>0, 使得f(u)≥(λ1+ε)u-m, ?u∈[0,+).取 不妨假設A在?BR1上無不動點(否則結論已成立). 需要證明 x-Ax≠ωx*, ?x∈?BR1∩P,ω≥0 (21) (反證法): 假設存在x2∈?BR1∩P以及ω1>0使得 x2-Ax2=ω1x* 故知x2∈K. 因為T(P)?K,x*∈K. 由引理2及(20)式得 x2(t)=Ax2(t)+ω1x*(t)= λ1Tx2(t)+ω1x*(t),t,s∈(0,1) (22) 因此由(22)式, 有 x2≥λ1Tx2+ω1x*≥ω1x* (23) λ1Tx2≥ω*λ1Tx*=ω*x* 那么根據(jù)(23)式可以得出 x2≥λ1Tx2+ω1x*≥(ω*+ω1)x* 這與ω*的定義相矛盾, 故(21)式成立, 根據(jù)引理5可得 (24) 由(19)式可知,存在0 f(u)≤λ1u, ?u≤r (25) 需要證明 Ax≠μx, ?x∈?Br∩P,μ≥1 (26) (反證法): 假設存在x3∈?Br∩P以及ω2≥1使得Ax3=ω2x3. 假設ω2>1, 則x3∈?Br∩P. 由(25)式可得:ω2x3=Ax3≤T2x3. 另外, 有ω2nx3≤T2nx3(n=1,2,…) 即 通過Gelfand公式可以推出 這與r(T2)=1相矛盾, 故(26)式成立, 根據(jù)引理6可得 (27) 因此, 由(24)式和(27)式可得 [1]ZHANGS.MonotoneiterativemethodforinitialvalueprobleminvolvingRiemann-Liouvillefractionalderivatives[J].NonlinearAnal, 2009, 71: 2 087-2 093. [2]ZHANGS.Positivesolutionstosingularboundaryvalueproblemfornonlinearfractionaldifferentialequation[J].Comput.Math.Appl, 2010, 59: 1 300-1 309. [3]ZHANGX.Positivesolutionsforaclassofsingularfractionaldifferentialequationwithinfinite-pointboundaryvalueconditions[J].Appl.Math.Lett, 2015, 39: 22-27. [4]CUIY.Uniquenessofsolutionforboundaryvalueproblemsforfractionaldifferentialequations[J].AppliedMathematicsLetters, 2016, 51: 48-54. [5]ZHAOY,SUNS,HANZ,etal.Positivesolutionstoboundaryvalueproblemsofnonlinearfractionaldifferentialequations[J].Abstr.Appl.Anal., 2011(16):6 950-6 958. [6]ZOUY,LIUL,CUIY.Theexistenceofsolutionsforfour-Pointcoupledboundaryvalueproblemsoffractionaldifferentialequationsatresonance[J].Abstr.Appl.Anal, 2014(13):286-299. [7]ZHANGX,LIUL,WUY.Multiplepositivesolutionsofasingularfractionaldifferentialequationwithnegativelyperturbedterm[J].Math.Comput.Modelling, 2012, 55: 1 263-1 274. [8]KILBASA,TRUJILLOJ.differentialequationsoffractionalorder:methods,resultsandproblemsII[J].Appl.Anal,2002, 81: 435-493. [9]LIUZ,LIF.Multiplepositivesolutionsofnonlineartwo-pointboundaryvalueproblems[J].J.Math.Anal.Appl, 1996, 203: 610-625. [10]MAR.Existenceofsolutionsofnonlinearm-pointboundaryvalueproblems[J].J.Math.Anal.Appl, 2001, 256: 556-567. [11]ZHANGG,SUNJ.Positivesolutionsofm-pointboundaryvalueproblems[J].J.Math.Anal.Appl, 2004, 291(2): 406-418. [12]O′REGAND.Theoryofsingularboundaryvalueproblems[M].Singapore:WorldScientific,1994:168. [13]ARIASM,GONZALEZM.Positivesolutionstooperatorequations[formulaomitted] [J].LinearAlgebra&ItsApplications, 2010, 433(6): 1 194-1 202. [14]郭大鈞, 孫經(jīng)先. 非線性積分方程[M]. 濟南:山東科技出版社,1987. [15]MAR,ZHANGJ,FUS.Themethodofloweranduppersolutionsforfourth-ordertwo-pointboundaryvalueproblems[J].Math.Anal.Appl., 1997, 215: 415-422. [16]AGARWALR.Onfourth-orderboundaryvalueproblemsarisinginbeamanalysis[J].DifferentialIntegralEquations, 1989(2): 91-110. [17]DEIMLINGK.NonlinearFunctionalAnalysis[M].NewYork:Springer,1985. (編輯:郝秀清) Positive solution for boundary value problems for fractional differential equations ZHAO Cong1,WEI Shuai-shuai2 (1.College of Mathematics and System Science, Shandong University of Science and Technology, Qingdao 266590, China;2.School of Mathematics, Liaocheng University, Liaocheng 252059, China) positive solution; first eigenvalue; fixed point index 2016-09-09 國家自然科學基金項目(11571207) 趙聰, 男,sdustcyj@163.com 1672-6197(2017)03-0011-04 O A
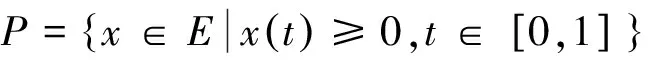
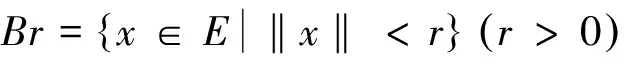
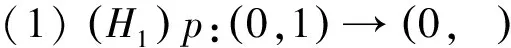
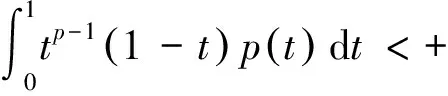
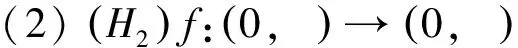
1 預備知識
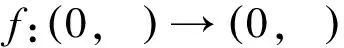
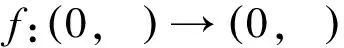
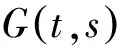
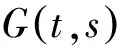
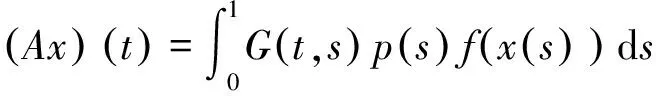
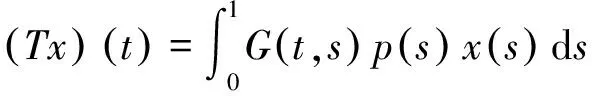
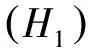
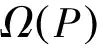
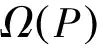
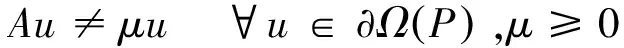
2 主要結果