B樣條快速求值改進CST參數化方法*
閆博文 黃 俊 劉志勤 王耀彬
西南科技大學計算機科學與技術學院,四川綿陽 621000
隨著航空航天技術的發展和國防科技的需求,飛行器的外形設計越來越受關注,飛行器設計的第一步便是外形參數化,它的優劣程度對于飛機設計的成功與否有著至關重要的影響,直接影響著總體項目的進度。一個好的參數化方法應該具備以下特性:1)較大的尋優空間;2)良好的局部控制能力,以及較少的設計變量;3)保證在優化過程中飛機的幾何外形是光滑的[1-2]。
Kulfan和Bussoletti提出了一種比較優秀的參數化方法:CST技術。CST技術同時使用類別函數與形狀函數來對外形進行控制,類別函數(Class Function)生成幾何圖形的基本外形,再通過形狀函數(Shape Function)對這個基本的幾何圖形進行修正,從而得到所需要的幾何外形。因該技術具有設計變量少,可調節,設計空間廣,可產生光滑的幾何外形,以及較好的魯棒性等優點而被廣泛應用在飛行器外形參數化的設計中[3-5]。由于Bezier多項式對局部幾何特性描述能力不足,王迅等人提出了使用B樣條函數替代Bezier多項式構造形函數的改進方法,以提高對外形的局部描述能力[6],因為B樣條方法在數據的擬合、平滑和插值等方面有良好的效果,所以在階數較小的情況下,該方法確實起到了優化作用。但B樣條基函數為分段函數,無法使用統一的解析式表達,大多使用迭代方法求值,會出現多次重復計算,隨著階數的增加,計算量也急劇增加,文獻[6]也只采用了3階來進行證明。因此,只有解決B樣條在高階數計算量大的問題,找出一種快速求解的算法,提高運算效率,才能讓B樣條改進CST方法發揮出更大的價值。因此,本文主要研究B樣條基函數快速求值改進CST算法。
1 B樣條替代Bezier多項式建模
1.1 B樣條基函數定義
B樣條的基函數有許多定義方法,它們中最被大家廣泛認可的是de Boor-Cox遞推定義法,因為de Boor-Cox遞推定義充分展示了B樣條基函數的性質,并給出了明確的B樣條基函數遞推求解算法,故本文將其作為B樣條基函數的標準定義[7]。
基函數定義:
(1)
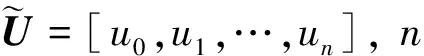
1.2 替代Bezier多項式的CST方法建模
一般機翼的CST方法數學表達式:
(2)
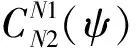
(3)
修改后的B樣條基函數CST公式對求解時出現的病態現象有很大的緩解,求解更加穩定,具有很好的局部描寫能力。
2 B樣條基函數快速求值算法
2.1 de Boor-Cox算法弊端
在實際計算B樣條時,往往不需要將整個B樣條數值全部計算出來,有時只需要計算某一參數值處的B樣條基函數。由B樣條局部支撐性質,可知當參數u∈[ui,ui+1),只需計算出Nm,k(u),m=i-k,i-k+1,…,i;而其他k次B樣條在該處均為0。
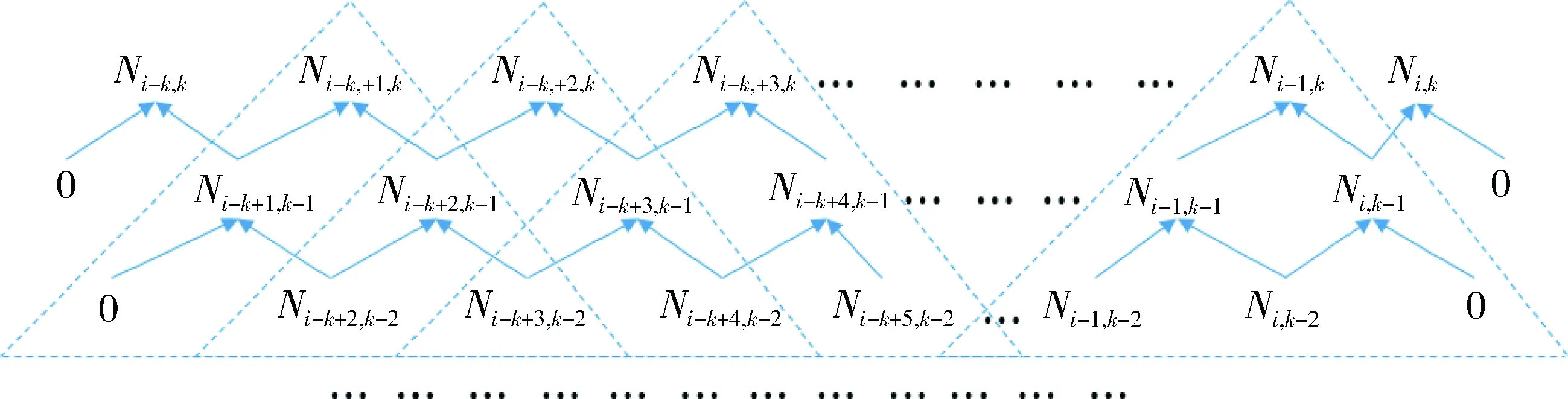
圖1 B樣條基函數運算路徑
圖1中,B樣條基函數計算過程已用虛線三角形標出,可以直觀的看到,每一個基函數不僅依賴于它下一層相鄰的2個基函數,而且還影響它上一層相鄰的2個基函數。顯然,式(1)的計算方法并不能充分利用這種網格結構,存在大量的重復計算,例如2個虛線三角形重疊的部分就是重復計算的部分,故而要加快B樣條基函數求解效率就要從這里著手。
2.2 準備工作
為后續闡述B樣條基函數快速求值首先定義一種向量擴展算法。
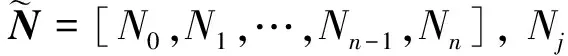
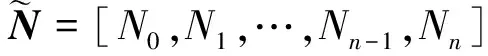
Zj=Nj+Qj-1-Qj
(4)
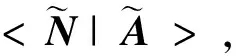
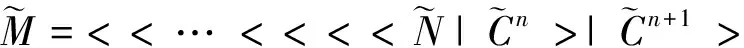
這種遞推式的運算有利于使用計算機運算,稱定義3給出的運算為向量遞推擴展運算。
2.3 快速求解算法證明[8]
首先,對將要使用的符號進行說明:
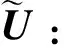
Nj,m(u):表示m次B樣條第j個樣條基函數,其中,m=0,1,2,…,k;j=1,2,3;
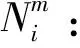
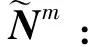
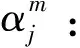
(5)
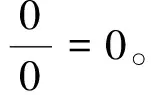
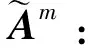
證明B樣條基函數快速求值前,還需證明引理1。
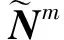
根據定義2的向量擴展運算法,則有:
(6)
其中:0≤j≤m,規定向量下標溢出時對應元素置0。
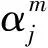
(7)
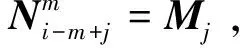
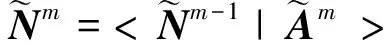
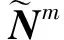
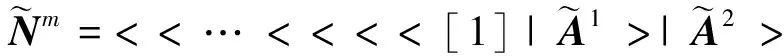
再由定義(1)可知:
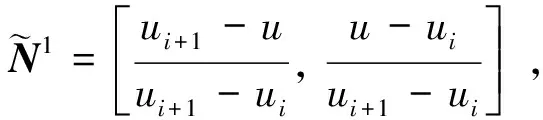
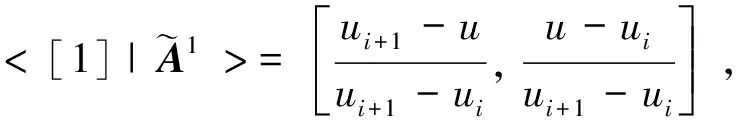
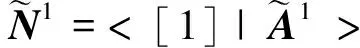
定理1提供了實現B樣條基函數求值的向量遞推擴展方法。其計算路徑如圖2。由圖2可知,B樣條基函數向量擴展快速求值方法正是一種網狀計算結構,它是以1維的單位向量{[1]}為主向量,通過遞推擴展,實現了同次數B樣條基函數值的同步計算(圖2中虛線方框部分)。向量遞推擴展方法避免了重復計算,提高了計算效率,這由圖2算法計算路徑沒有重疊部分可以充分說明。綜上所述,B樣條的向量擴展求值算法在計算路徑上比式(1)的de Boor-Cox算法效率更高。
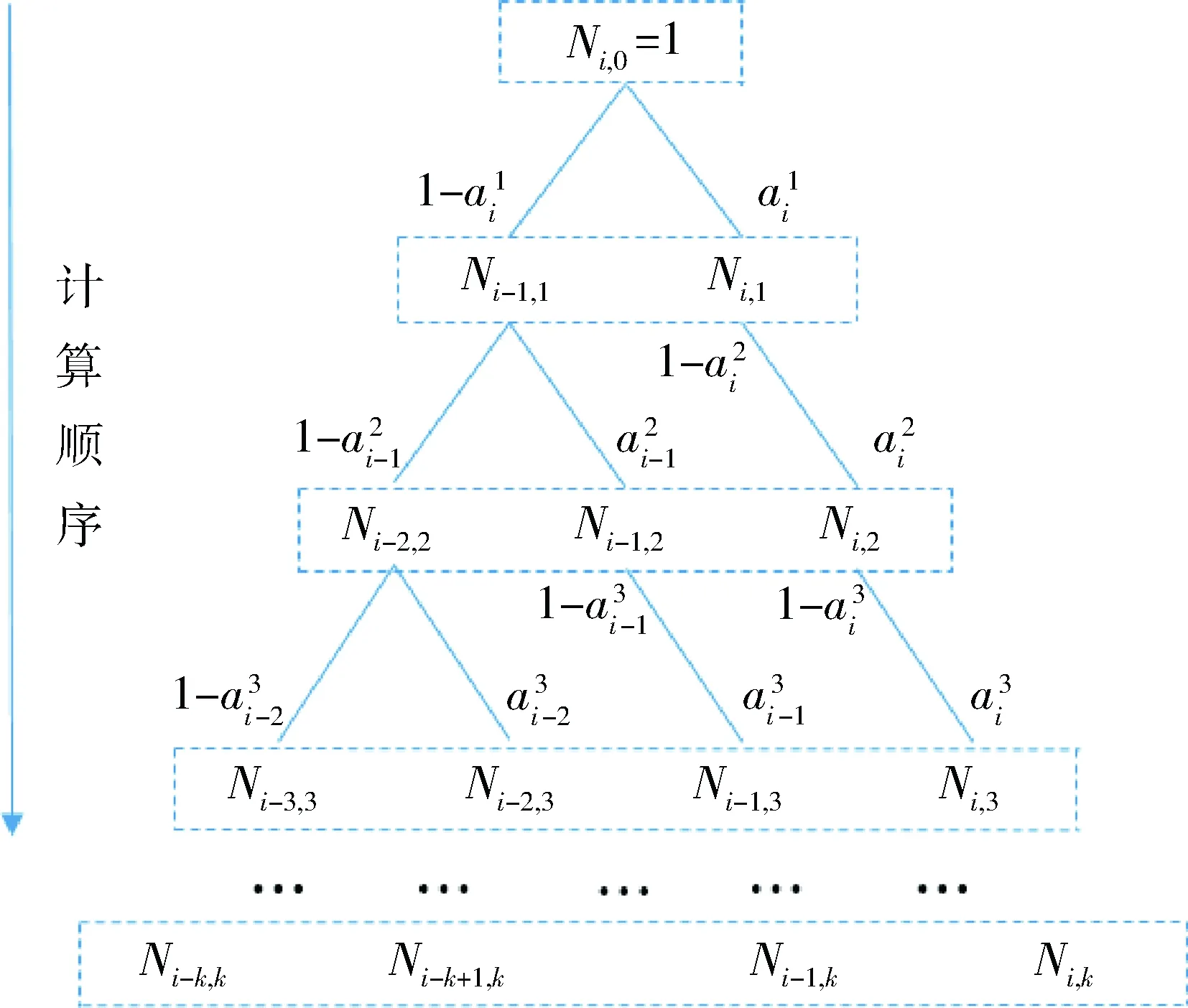
圖2 B樣條向量擴展法基函數運算路徑
2.4 算法效率
同de Boor-Cox遞推定義法相比,式(4)的B樣條基函數向量擴展求值算法效率更高,計算k次B樣條基函數非零值,統計對比式(1)與式(4)的運算次數,可得:使用向量同步遞推運算獲得k+1個非零基函數值的計算效率是使用de Boor-Cox遞推方法的2k+1倍。

表1 k次B樣條的(k+1)個非零基函數運算量對比
3 應用展示
3.1 B樣條快速求值CST二維建模
圖3為使用B樣條快速求值CST方法生成的二維圖形。
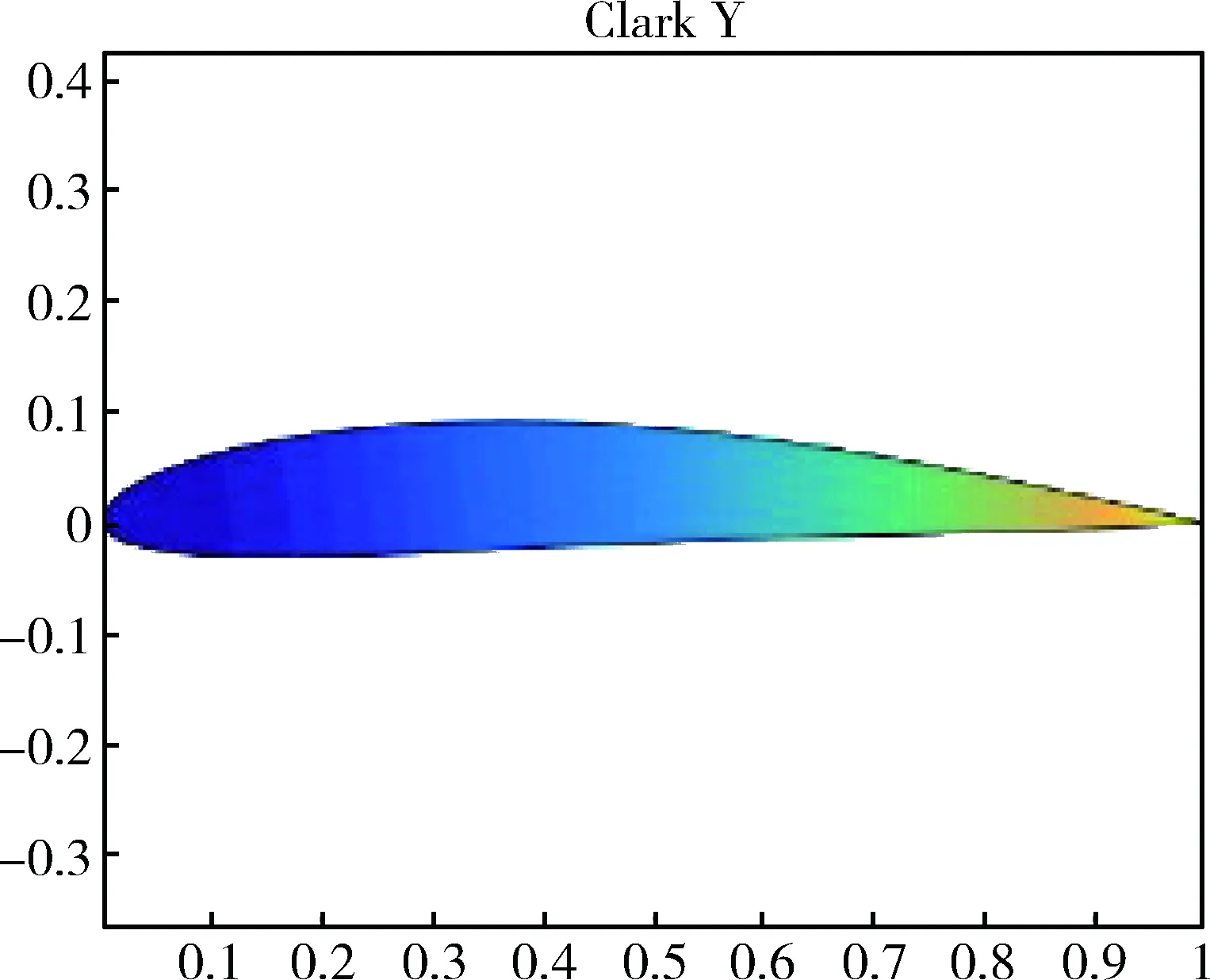
圖3 B樣條向量擴展法模擬Clark-Y機翼
3.2 B樣條快速求值CST三維建模
3.2.1 局部控制展示
圖4中,(a)圖展示使用B樣條快速求值方法控制橫截面從圓形漸變到正方形,(b)圖展示截面函數指數NC隨著長度的增加而進行變化,若將該立體圖形的總長度視為100%,在總長度的0%~20%區間內,立體圖形的橫截面是標準圓形,NC=0.5;在總長度的95%~100%區間內,立體圖形的橫截面是標準的正方形,NC=0.005,在總長度的20%~95%區間內,函數指數隨長度的增加而減小。
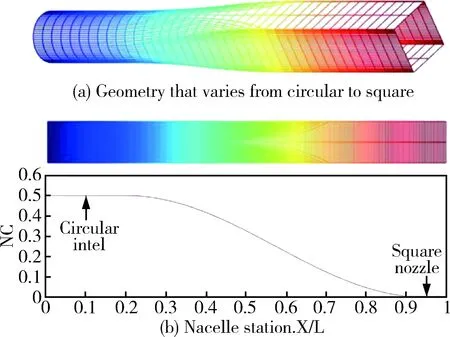
圖4 B樣條快速求值局部控制展示
3.2.2 B樣條快速求值CST方法三維機翼
三維機翼其實本質上可以看成是二維機翼的擴展,擴展時需要注意控制外形的變化。
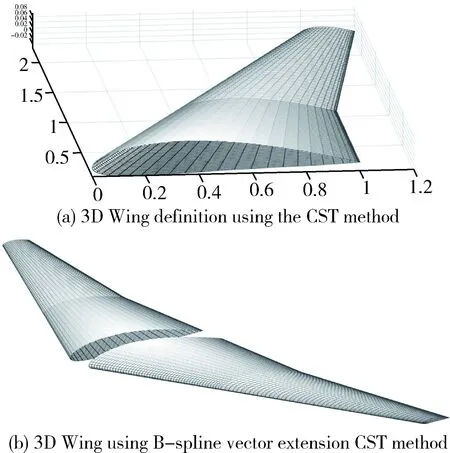
圖5 CST算法三維機翼展示
4 結論
通過B樣條改進CST參數化方法,提高了CST算法的局部控制能力,同時使用向量擴展方法實現B樣條快速求值,提高了B樣條CST算法的計算效率,增大了設計空間,提高了可控性,為提高后續翼型氣動優化的精度,最終得到良好的氣動外形奠定了基礎。
[1] Isakova N P, Kraiko A A, P’Yankov K S. Direct Method for the Design of Optimal Three-dimensional Aerodynamic Shapes[J]. Computational Mathematics & Mathematical Physics, 2012, 52(11):1520-1525.
[2] 廖炎平, 劉莉, 龍騰. 幾種翼型參數化方法研究[J]. 彈箭與制導學報, 2011, 31(3):160-164.(Liao Yanping, Liu Li, Long Teng. The Research on Some Param-eterized Methods for Airfoil[J]. Journal of Projectiles Rockets Missiles & Guidance, 2011, 31(3):160-164.)
[3] Kulfan B. A Universal Parametric Geometry Representa-tion Method - "CST"[C]. AIAA--2007-0062, Jan 2007
[4] Kulfan, B. M, Bussoletti, J. E., Fundamental Parametric Geometry Representations for Aircraft Component Shapes[C]. AIAA-2006-6948, 11th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference: The Modeling and Simulation Frontier for Multidisciplinary Design Optimization, 6 - 8 September, 2006
[5] Ciampa P D, Zill T, Nagel B. CST Parametrization for Unconventional Aircraft Design Optimization[C].Congress of the International Council of the Aerospace Sciences. DLR, 2010.
[6] 王迅, 蔡晉生, 屈崑,等. 基于改進CST參數化方法和轉捩模型的翼型優化設計[J]. 航空學報, 2015, 36(2):449-461.(Wang Xun,Cai Jinsheng,Qu K,et al. Airfoil Optimization Based on Improved CST Parametric Method and Transition Model[J]. Acta Aeronautica et Astronautica Sinica,2015,36(2):449-461.)
[7] Piegl L, Tiller W. The NURBS, Book[M]. Springer Ber-lin Heidelberg, 1997.
[8] 孫海洋, 范大鵬. B樣條快速求值算法及其在數控插補中的應用[J]. 計算機工程與應用, 2007, 43(34):81-84.(Sun Haiyang, Fan Dapeng.Fast Algorithm to Compute B-spline Functions and Its Application in CNC Interpolation[J]. Computer Engineering and Applications,2007,43(34):81-84.)

