Java數字音頻識別程序

侯昶宇

【摘要】 本文主要討論java實現聲音識別程序，采用mfcc參數提取以及混合高斯模型方法。使用mfcc處理聲音得到音頻的特征參數后，通過混合高斯模型建模實現對音頻的判別。最終通過JNI方法將windows下程序移植到Android端下運行。

【關鍵詞】 梅爾倒譜系數 混合高斯模型 目標識別

一、背景及應用

對于聲音識別技術來說，由于不需要過多接觸以及實體間交互模式的認證，因此，它在使用中比其他種類的識別技術更加便利。而在配置過程中，由于當前多數電子數碼產品都已經安裝了聲卡和話筒，因而構架上也可以節約更多的成本。此外，對于使用環境來說，由于不需要如視頻監控設備那樣對角度有著較高的要求，所以聲音識別系統的使用環境無疑也會更加的隨意和隱蔽。這些都是聲音識別系統與其他安防設施相比更加獨特的優勢。

除了常見的安防系統應用以外，其實日常生活中一些身份識別也采用聲音識別模式。現在，很多銀行都采用了聲音識別的模式進行保險箱的控制；或者在一些遠程的服務中，也采用聲音識別的模式，對客戶的身份進行定位。此外，作為智能化技術的重要一環，聲音識別同樣可以用于智能家電。盡管這種全新的模式在短時間之內普及，無論是在技術上還是理念上都會遇到不小的阻力。但從長遠來看，這種技術的出現以及民用化的普及，對于未來實現個人信息的全方位保護將起到標志性作用。

二、聲音識別程序概述

首先將音頻文件讀作浮點數數組指針采樣點，之后將數組建立混合高斯模型，再將讀取的結果和已經保存的混合高斯模型做比較，從而得出與高斯模型中最接近的結果。

2.1高斯模型

高斯模型就是用高斯概率密度函數（正態分布曲線）精確地量化事物，將一個事物分解為若干基于高斯概率密度函數（正態分布曲線）形成的模型。

2.2統計學習模型

我們常用所謂統計模型的學習分為概率模型和非概率模型。概率模型指的是模型訓練方式為P=（Y|X）的類型。輸入X后得到的不是具體值，而是一系列的概率，我們選取概率最大的作為判決對象。與之相對的，非概率模型的形式是y=f（x）。輸入x后得到唯一結果y，并以其作為判決對象。

2.3梅爾頻率倒譜系數

由于不同的人有不同的特異性特征，所以先采用預加重技術，即插入一個高通濾波器，從而加強聲道部分特征。高通濾波的傳遞函數如下：

H（Z）=1-αZ-1

因聲音在短時間內呈現平穩性，所以之后進行分幀和加窗。同時為了避免丟失信息，相鄰幀之間還應存在重疊。

再對分幀加窗后的各幀信號進行FFT變換得到各幀的頻譜。并對語音信號的頻譜取模平方得到語音信號的功率譜。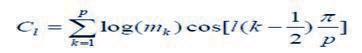

最終通過濾波和離散余弦變換得到的Ci即為所需提取的特征參數。

2.4混合高斯模型的建立

建立混合高斯模型，及對樣本的概率密度分布進行估計，估計采用的模型是幾個高斯模型的加權和，每個高斯模型作為一個類，將樣本數據分別投影到幾個高斯模型時，就能得到在各個類上的概率。最終選取概率最大的類作為判決結果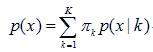

上式中，K衛模型個數，πk為第k個高斯模型的權重，p為第k個高斯模型的概率密度。求出p（x）后，求和的各項結果分別代表x屬于各個類的概率。

通過上述方法，可以進行訓練在資料庫中加入新的聲音訓練得到的gmm模型，還可以通過與已知的gmm模型進行比對從而識別聲音種類。

三、Android實現

Android上層的Application和Application Framework都是使用Java編寫，底層包括系統和使用眾多的LIiraries是C/C++編寫的。所以上層Java要調用底層的C/C++函數庫必須通過Java的JNI來實現。

在進行JNI操作時，首先，使用eclipse得到一個app文件，此處，eclipse會自動編譯此java文件。編譯后的文件在bin目錄下，通過javah命令生成一個c++的頭文件。在根據這個頭文件編寫c++程序。將windows下運行成功的程序中的函數編譯為.so文件作為java編譯時的庫函數。在進行java編程時，只需要對c++函數進行合理調用即可。

四、實驗結果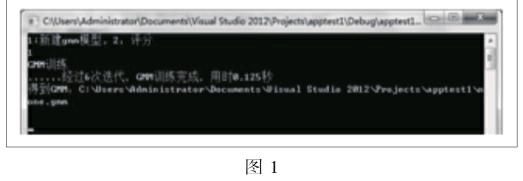

通過六次迭代后得到gmm模型并添加進數據庫，見圖1。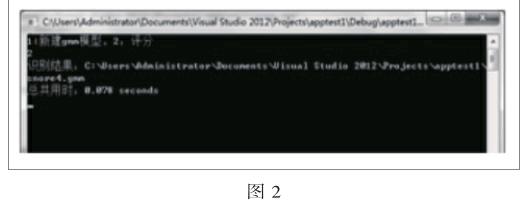

得到gmm模型后與數據空內已有模型進行比較，從而選出最接近的聲音是已有聲音模型中的一個，見圖2。

在Android端實現聲音識別， 見圖3。

四、總結

一個完整的聲音識別模塊應該有一下幾部分組成：前段處理、聲音建模、聲音數據庫、匹配判決。根據以上流程，本文所設計的聲音識別程序從過mfcc對聲音進行處理，之后建立高斯混合模型，在添加足夠的聲音種類進入數據庫后可以對聲音進行識別。通過JNI方式移植到java平臺后，使其應用更加廣泛。

參 考 文 獻

[1] C library for computing Mel Frequency Cepstral Coefficients （MFCC）

[2] Freeman H. On the Encoding of Arbitrary Geometric Configurations. IRE Trans. Electronics and Computers， 1961， 10：260-268

[3] Ballard D H. Generalizing the Hough Transform to Detect Arbitrary Shapes [J]. Pattern Recognition， 1987， 13（81）：111-122.