基于詞匯聚類方法的現代漢語分期與分期體系構建

饒高琦，李宇明

(1. 北京語言大學 對外漢語研究中心,北京 100083；2. 北京語言大學 語言政策與標準研究所,北京 100083)

0 引言

進行有關現代漢語歷史變遷的研究無法不涉及分期問題。以往對現代漢語史的研究多直接借用政治史的分期方式將現代漢語分為新文化運動到1949年、1950—1966年、1967—1976年和1977—至今四個時期，并在這一基礎上開展了許多研究[1-4]。雖然語言生活，尤其是本文使用的報刊歷史語料，在內容上與政治生活有密切聯系，但語言系統有其自身的演變規律。從語言數據出發對語言進行分期是更加合適的選擇。傳統的分期方法缺乏定量分析，往往根據相對孤立的語法現象和語法點進行分析，無法根據廣泛的語言使用情況來獲得較合理的分期依據。

本文將語言的分期落實在語料的分期中。語料的分期則可以視作不同時間文本的自然分組任務，即聚類問題。本文基于歷史的詞匯分層工作的結果[5-6]，使用機器學習方法對歷史語料庫中的文本進行自動聚類。以期從詞語使用的角度，進行定量的歷史語料時期劃分。

1 基礎工作

1.1 歷史語料庫

本文使用的語料為BCC歷史檢索系統*http://bcc.blcu.edu.cn/hc.[7-8]中1946年到2015年的《人民日報》語料*由于種種原因，本文實驗過程中沒有獲得2003年到2008年的《人民日報》語料，該部分由實驗室積累的相應年份的《貴州日報》替補。，時間跨度70年，規模12億字。使用GPWS通用分詞系統*宋柔,羅智勇. 現代漢語通用分詞系統(GPWS v3.5)http://democlip.blcu.edu.cn:8081/gpws/.[9]并輔之以小規模人工修正對歷史語料庫進行分詞，詞種數約220萬。

1.2 時間敏感詞

饒高琦[5]基于70年跨度的歷史報刊語料庫，使用了包括TF-IDF、互信息、聯合熵、變異系數、詞項隨機采樣、修正頻率、累積頻率等九種統計方法計算了詞匯在歷史中的使用穩定性，并通過對穩定性、覆蓋度和時間區分性能的考察，確定了以月為劃分文本的時間顆粒度、以TF-IDF為主的計量方法，并獲得了規模為3 013詞的歷時穩態詞候選詞集。其中詞語的時間敏感性極差，包括功能詞和基本名詞等，構成語言生活的底層，即基干層。

饒高琦[6]發現，基干層之外的詞匯中，以月顆粒度計算TF-IDF值按降序排列，第10 000到50 000位之間的詞匯對時間變化較為敏感，且平均頻次較大，例如，合作社、非典、撥亂反正等。它們與快速出現獲得較高頻次，但迅速退出使用的命名實體有很大不同。這部分詞匯構成了時間敏感層。許多時間敏感的社會語言現象多由這一層中的詞語構成。流行語和年度詞亦多出自此層。

1.3 聚類算法

本文選擇K均值算法和期望最大化算法對歷史語料庫中的文本進行聚類，并使用機器學習平臺Weka*http://www.cs.waikato.ac.nz/ml/weka/.[10]實現。

K均值(K-means)算法是一種十分常用的聚類機器學習算法，也是一種基于距離的迭代聚類算法[11]。本文中的K均值算法采用歐氏空間距離。其優點是可以確保一個類中每個實例到中心的距離平方和最小。但聚類數量K需要人工指定，且只能獲得局部距離平方和最小值。通常通過對不同K值進行多次實驗來尋找較優的聚類數量，對特定K值進行多次實驗則可以在一定程度上克服無法獲得全局最優聚類的缺陷。根據經驗K均值方法中的聚類數K?N，N為樣本數量，在本文中就是歷史語料的年數。

期望最大算法(expectation-maximum algorithm)是一種基于統計的聚類方法，其基礎是建立一個限混合(finite mixtures)統計模型[12]。期望最大算法在給定一個(隨機)初始值后不斷進行迭代，進行重新估計直到收斂。該算法的優勢在于無需事先指定聚類數量(分布的數量)，但同樣不能保證收斂于全局極大值。為了有機會獲得全局極大值，需要對同一組數據進行多次試驗。

2 對歷史語料進行聚類

本文在歷史語料庫中提取各年度的詞表，使用基干層詞匯和時間敏感層(簡稱詞敏層)詞匯兩個時間敏感性幾乎相反的詞集進行處理，以獲得進行聚類實驗的特征集，處理方法如下。

處理A在第i年詞表Lexi中保留出現的時敏層詞匯Ssens，即FAi=Lexi∪Ssens。FAi為第i年的特征集。

將兩種方法處理后獲得的特征集FAi和FBi中的詞當作聚類特征，把其在當年的頻率當作特征值，分別使用K均值和期望最大化兩種方法進行聚類。語料的時間顆粒度為年。

由前文已知K均值和期望最大化算法的缺陷，每種實驗設定均對相同數據進行五次實驗以獲得穩定的聚類結果。表1是K均值選取不同聚類數時的聚類結果。

表1 K均值在不同聚類數時的實驗結果

表2是期望最大化算法自動獲得聚類數時的聚類結果。

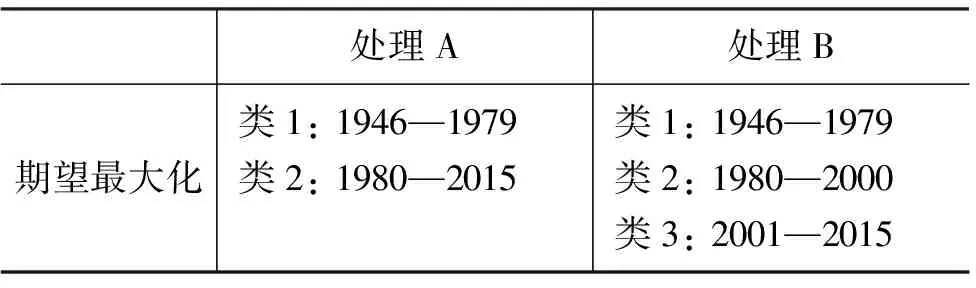
表2 期望最大化算法實驗

語言的演變是連續而漸進的，依據語言特征的時間演變進行聚類，其結果在時間軸上也應當是連續的，即一個聚類應由年份連續的語料組成。

通過對表1的觀察，發現處理A僅在聚類數量增加到7的時候開始出現類和類之間互相穿插的現象，如類1和類2將彼此切割成了3段和2段。處理B在許多實驗的聚類數量下容易出現類和類之間互相穿插的現象。如K=2和3時類1被類2截為兩段；K=6時類1和類2則互相穿插多次，而且K>2的聚類中始終都存在一個孤立點。這與語言演變具有漸變性的認知有較大的沖突。因而處理B在使用K均值算法進行的聚類中并不是一種好的選擇。處理A在聚類數量增加到7時，聚類質量也開始變差。下一節將選擇聚類數從2到7的實驗進行分析。

我們嘗試對處理B的較差效果進行解釋。處理B是將每年詞表去除出現在當年的基干層詞后的結果。每年語料的特征數量過于龐大，詞匯繁雜。其中既有時間敏感性略差的介于基干層與時間敏感層之間的詞匯，也有大量超低頻的出現時間極短的詞匯(大多是命名實體)。這些特征對聚類過程形成了一定干擾。

與K均值不同，在期望最大化算法的結果中，兩種處理方式都有較好的表現。期望最大化算法在處理B時的聚類結果和K均值算法中聚類數量K=3時的結果一致。期望最大化算法中使用處理A時的聚類結果和K均值算法中聚類數量K=2時的結果一致。這也在一定程度上使我們可以更確信地在后文中使用K=2和3時的K均值的聚類結果。

3 聚類結果分析

語言變化的速率是不均勻的。當變化較快，在一個特定時間單位(如年)內無法刻畫變化過程的時候，該時間單位就形成一個邊界。而較為緩慢的變化可以在幾個時間單位內被觀察到，這就形成了若干時間單位構成的一個過渡(地帶)，更加緩慢的變化以至于在很長一段時間內保持穩定，那么就形成了前文中所描述的一個聚類，其現實意義就是一個時期。本節通過這三種方式對聚類結果進行分析，從而獲得語言使用的時期信息。

K均值在不同聚類數量下的聚類結果給我們提供了一扇觀察歷史語料分期，尤其是歷史詞匯使用分期的窗口。K均值在處理A的特征集FAi的實驗中存在一些較為穩定的聚類邊界。如1979—1980年的邊界在聚類數為2、3和4時均無變化，在聚類數為5、6時變化為1977—1978年邊界和1978—1979年邊界。聚類邊界的移動或變化是算法受聚類數量影響的結果。但其移動幅度小說明類的聚類比較穩定。聚類的小幅度移動也符合對語言使用演變是漸變的假設，剛性的邊界在語言使用的變化中可能不多見。因此本節將聚類的邊界模糊處理，即將較少的若干個樣本(即若干年的語料)視作兩個聚類的過渡，如1979—1980年邊界可以擴大為1977—1980年過渡。

聚類數為3時的2000—2001年邊界在聚類數量為4—6時可以擴大為1997—2002年過渡。聚類數為5時的1988—1989年邊界在聚類數量為6時可以擴大為1988—1990年過渡。聚類結果中也存在不變化或移動的邊界，如2007—2008年邊界在聚類數量為4時出現，在后來的實驗中保持穩定，并未變化。而1964—1965邊界出現的很晚(K=6時才出現)，也未移動或變化。

如果將上述邊界和過渡都整理到一張樹狀圖(圖1)中，就可以較清晰地看到1946—2015年歷史語料由詞匯使用來劃分的年代分期情況。

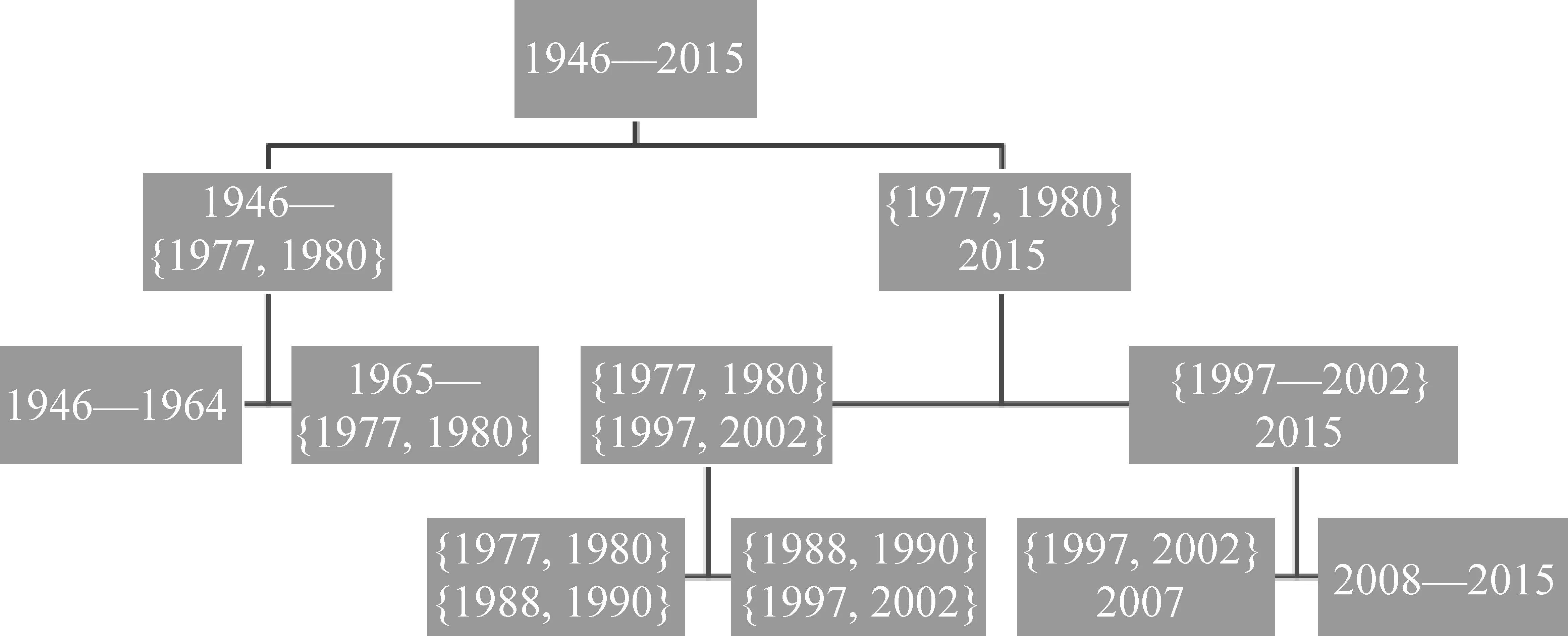
圖1 基于K均值方法的歷史語料詞匯使用分期

圖中，{m,n}表示年份m到年份n形成的過渡，如{1988,1990}為前文中描述的1988—1990年過渡。我們將邊界、過渡和聚類的數量同時映射到一張樹形圖上，可以得到圖2，以反映分期和聚類數量之間更直觀的關系。

圖3則將不同聚類數目中的分期結果繪制在時間軸上。深淺差異用來表示不同的聚類分裂的早晚和親疏關系。

如前文所述，這些“邊界”或“過渡”中，1977—1980年過渡和1997—2002年過渡也在期望最大化算法中出現，將語料分為兩個或三個相對穩定聚類。而它們出現時的實驗設定(K=2和3)也表明，如果只將歷史語料劃分為兩段，那么應該選擇1977—1980年進行切分。如果劃分為三段，應該再將80年代至今劃分為80年代到2000年和新世紀以來兩個階段。

這一劃分結果和對過去70年語言生活變遷的直觀感受基本相符。1977—1980年過渡是改革開放政策開始并逐漸起步的階段，語言使用的情況隨著國人思想的變化煥然一新。可以說改革開放的開始是過去70年詞匯使用變遷最重要的分水嶺。

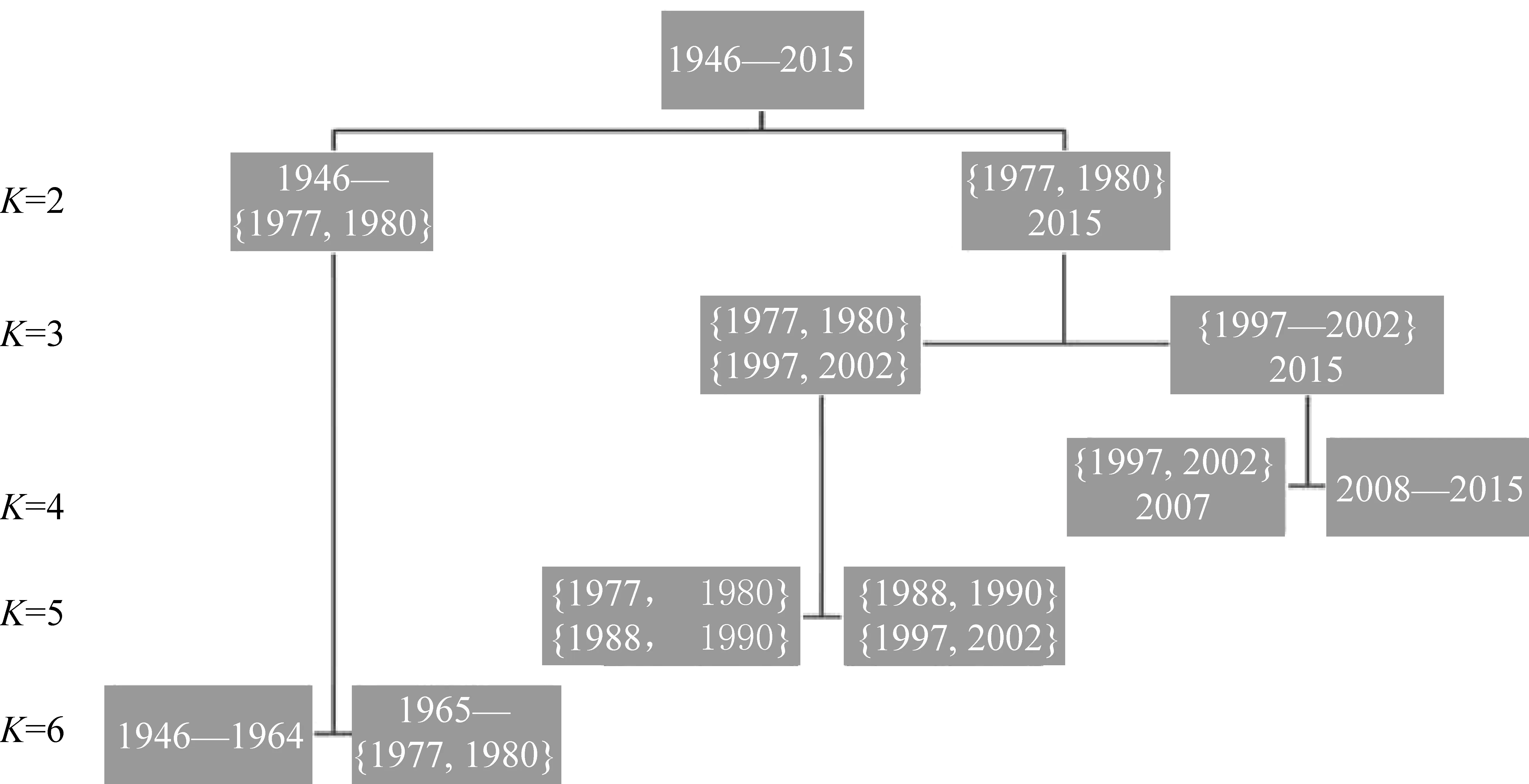
圖2 基于K均值方法的歷史語料詞匯使用分期及其聚類數量

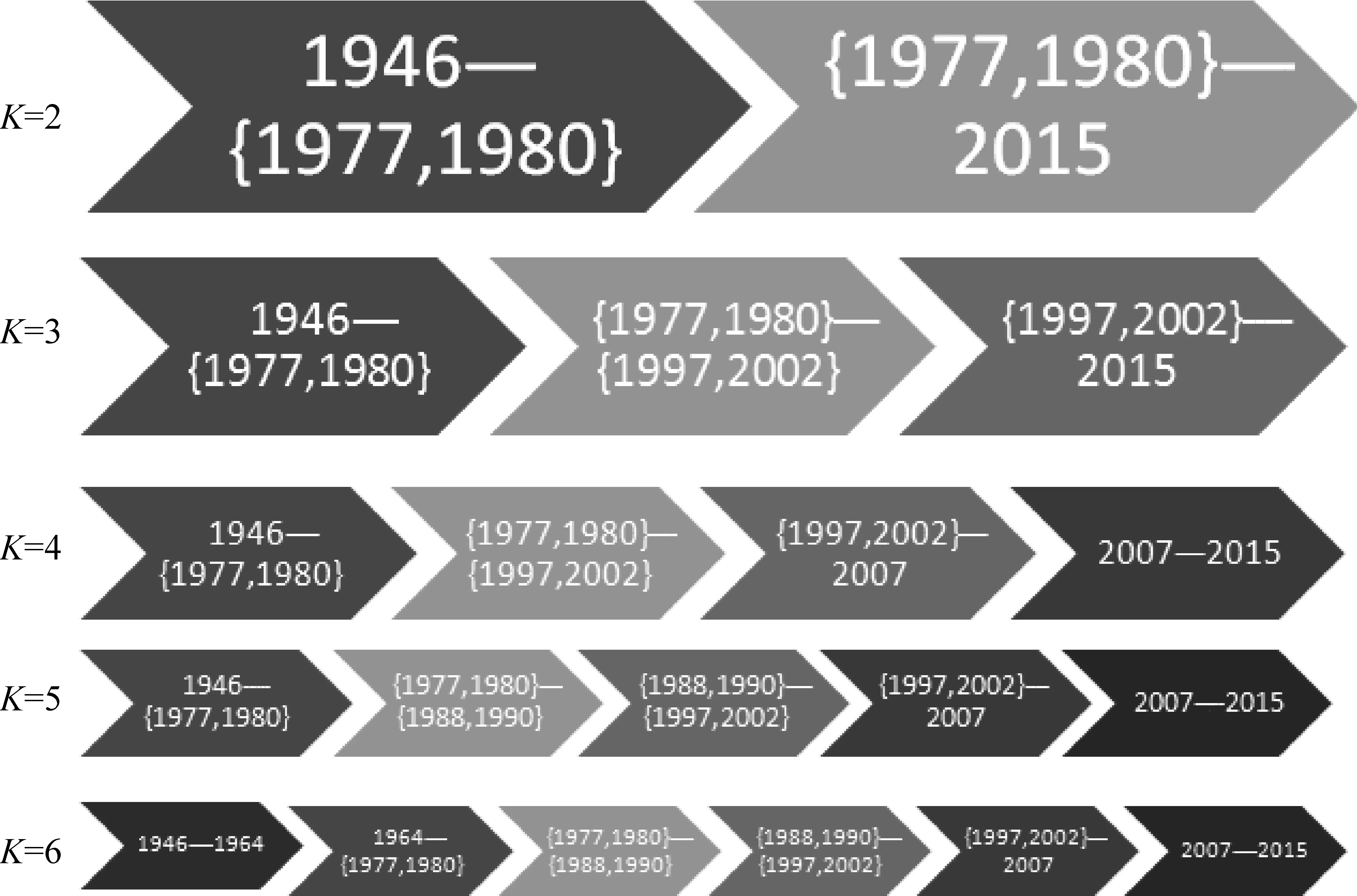
圖3 歷史語料詞匯使用分期及其聚類數量

1997—2002年過渡則是在改革開放漸入佳境，我國綜合國力高速上升的階段。語言生活和媒體的發展步入新的階段。但是這一過渡在已有的研究中很少被注意到。在刁晏斌[1-2]和Rao[3]的研究中， 都借用政治史將中華人民共和國成立后的現代漢語白話以文革運動為界分為三段。王建華[4]意識到“跨世紀穩定發展期”的存在，但是將1990年至今的時段劃為此段。涉及新政權建立前的語料，則簡單地以1949年為邊界分為兩段。并沒有注意到在詞匯使用的層面，新政權建立在語言上所產生的沖擊不如改革開放，甚至不如進入新世紀的影響大。

聚類的分裂率先從圖2第二層的右側(也就是圖3的第一層的淺色部分)開始。當二分類時的類2已經分裂為四個類的時候，二分類時的類1才開始分裂。這從一個側面展現了改革開放前后詞匯使用更新速度的差異。改革開放以前詞匯使用總的來說變化緩慢，該聚類較之改革開放后更為穩固，分裂得晚。

4 兩層三段分期體系

綜上所述，本文將1946—2015年共70年的歷史語料的時期劃分任務分為兩個層次。第一層次分為兩段，1946年到1977—1980年過渡為一段(E1)，之后為一段(E2)，并以1980年為實際操作時的邊界。第二層次分為三段，即第一層次中的第二段進一步分為1980年到1997—2002年過渡為一段(E2.1)，之后為一段(E2.2)，并以2000年為實際操作時的邊界。為行文簡便，后文中也使用E1、E2、E2.1和E2.2指代該分期體系中的時期。該體系示意如圖4所示。

圖4 兩層三段分期體系示意圖

對應Rao[3]在傳統分期方法下進行的詞語使用統計，本文在新的分期體系下對用詞情況進行了統計，如表3～5所示。

從表3容易發現： E2在詞語使用的豐富程度上大大超越E1，這在總詞種數和年均詞種數上都得到體現。在表4中比較年均詞種數可以發現E2.1處于最高峰。表5統計了各時期達到特定詞語覆蓋度(按詞頻降序獲得的詞匯累積頻率)所需的詞數。該組數據也刻畫了諸時期的詞語使用豐富程度，比例越高說明詞匯使用越豐富。表5數據體現出E2高于E1，E2.2高于E2.1高于E1的趨勢。這表明雖然高頻段詞種數在E2.1較多，但內部分布于E2.2更為平均，詞匯分布在高頻段更為多樣。總體而言，改革開放后(E2)的詞匯豐富程度有了明顯提高，并且呈現出先增長(E2.1)后回調(E2.2)的態勢，詞匯使用的多樣性持續增長。

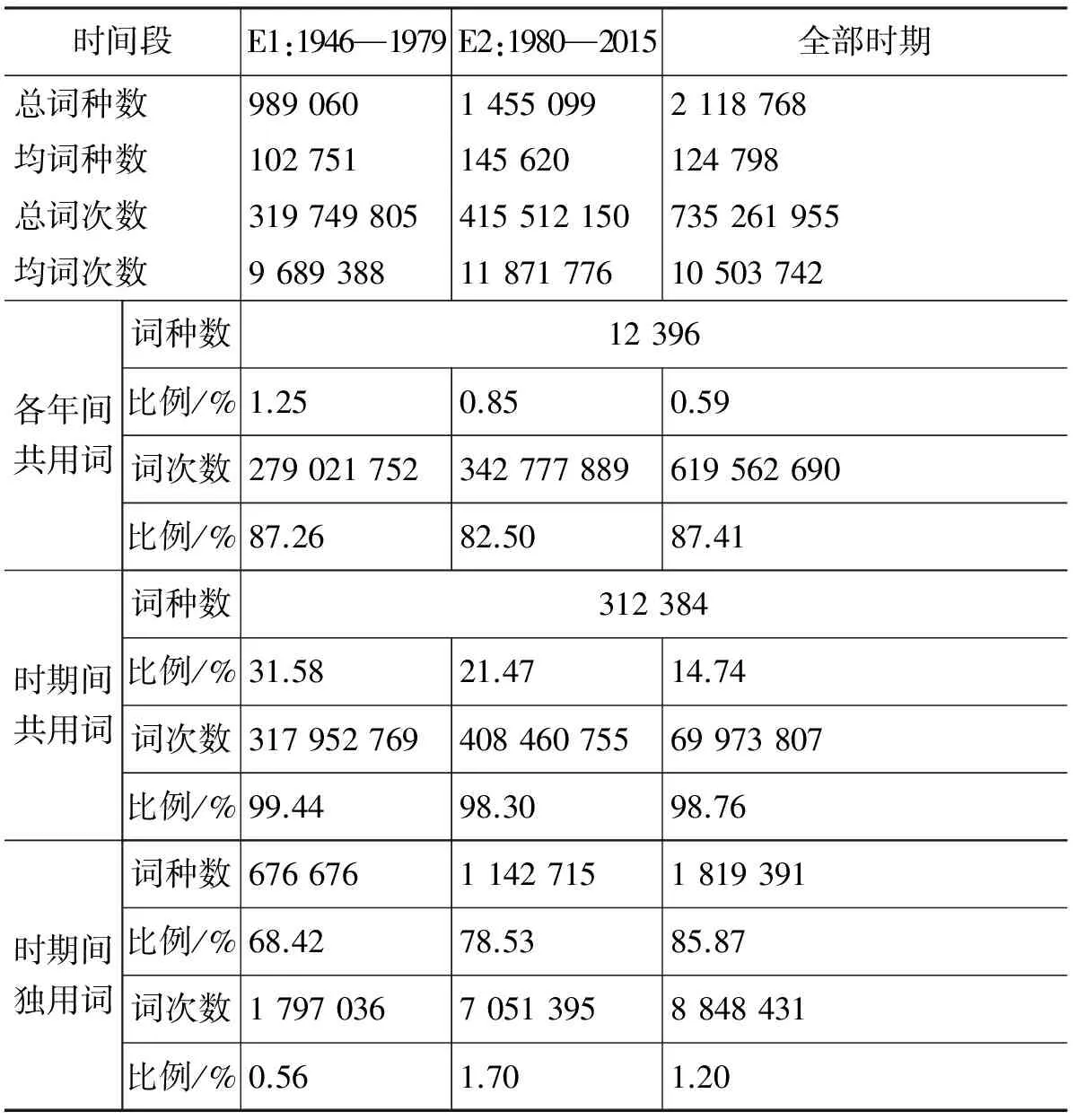
表3 在第一層次分兩段時各段的用詞情況

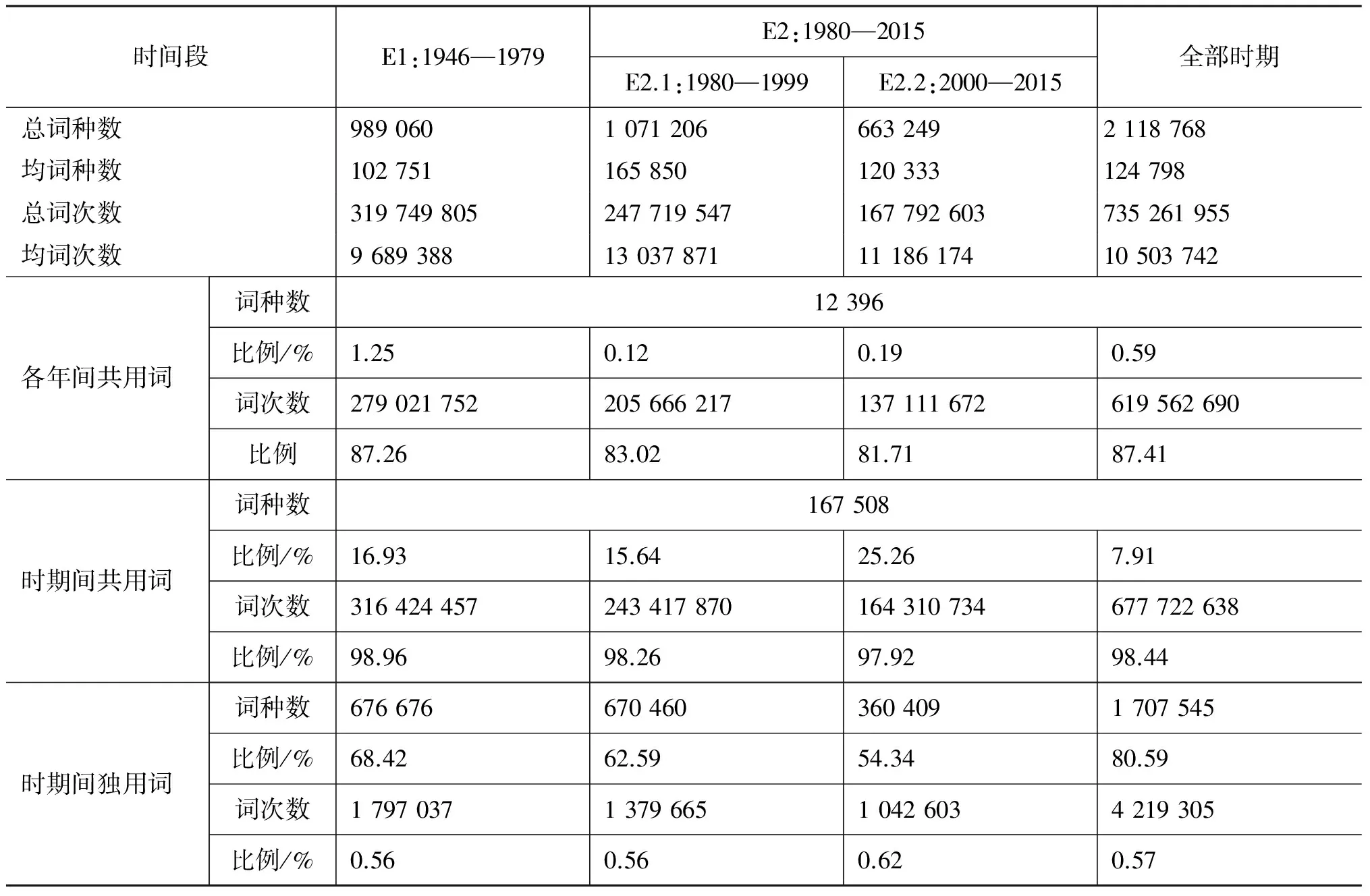
表4 在第二層次分三段時各段的用詞情況

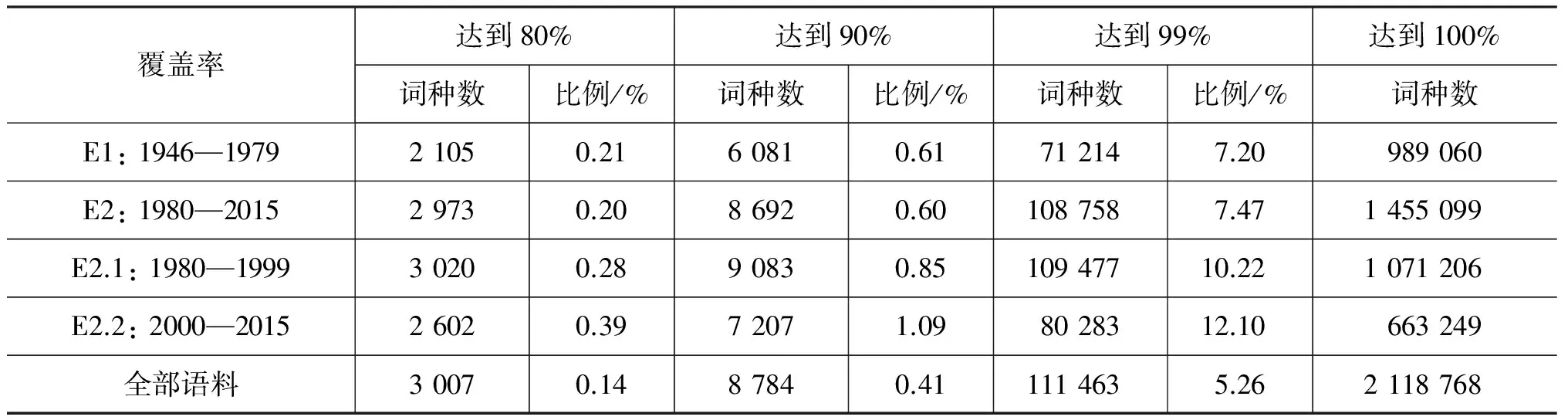
表5 各時期用詞覆蓋度

表3～5所示數據與傳統分期中用詞簡況[3]所展現的數據趨勢差異并不懸殊。首先是因為雙層分期體系依據時敏層詞的使用狀況而非全體詞匯的頻率進行分期， 表3和表4中著重分析的共用詞恰是基干層的重要部分；其次是因為時期的劃分本身具有一定的模糊性，這也恰恰表明僅僅通過對詞匯系統做整體的頻次統計，難以獲得時期劃分的線索。

5 小結

不同于過去借用政治史對現代漢語白話文進行分期的方法，本文工作使用統計聚類方法，以具有時間敏感性的詞匯的使用頻率為特征對70年跨度的報刊語料進行了聚類，尋找到了較穩定的聚類，并在不同的聚類數下繪制了具有層次性的詞匯使用分期樹。本文以1980年和2000年為實際操作邊界，構建了兩層三段分期體系。從純粹的語言學數據出發進行語言分期，打破了現代漢語白話文分期借鑒政治史分期的局面，揭示了把改革開放的開始作為過去70年間詞匯使用變遷最重要分水嶺的重要事實，世紀之交具有第二重要地位，并顯示了語言使用相對于社會變革的短暫滯后效應。

[1] 刁晏斌. 現代漢語史概論[M]. 北京： 北京師范大學出版社，2006.

[2] 刁晏斌. 現代漢語史[M]. 北京： 人民出版社，2006.

[3] Gaoqi R, Endong X. Words and characters in official newspapers since the foundation of PRC: Guizhou Daily and People’s Daily as Examples[C]//Proceedings of International Journal of Knowledge and Language Processing (IJKLP), 2015, 6(2): 23-33.

[4] 王建華，周明強，劉福根. 信息時代報刊語言跟蹤研究[M]. 杭州： 浙江大學出版社，2006.

[5] 饒高琦,李宇明. 基于70年報刊語料的現代漢語歷時穩態詞抽取與考察[J]. 中文信息學報,2016，30(06):49-58.

[6] 饒高琦,李宇明. 基于詞頻逆文檔頻統計的詞匯時間分布層次[C]//第十八屆漢語詞匯語義學研討會，樂山，2017.

[7] 荀恩東，饒高琦，肖曉悅，等.大數據背景下BCC語料庫的研制[J].語料庫語言學，2016, 3(1):93-118.

[8] 荀恩東，饒高琦，謝佳莉，等. 現代漢語詞匯歷時檢索系統與應用研究[J]，中文信息學報，2015(3): 169-176.

[9] 羅智勇. 現代漢語通用分詞系統的技術與實現[D]. 北京： 北京工業大學碩士學位論文, 2002.

[10] Ian H W, Eibe F, Mark A H. Data mining: Practical machine learning tools and techniques[M]. (3rd Edition). Morgan Kaufmann, 2011.

[11] Altman N S. An introduction to kernel and nearest-neighbor nonparametric regression[J]. The American Statistician,1992, 46 (3): 175-185.

[12] Dempster A P, Laird N M, Rubin D B. Maximum likelihood from incomplete data via the EM algorithm[J]. Journal of the Royal Statistical Society, Series B. 1977,39 (1): 1-38.