基于小波變換的圖像零樹壓縮感知方法

周四望+劉龍康

摘 要：稀疏性是壓縮感知的前提，然而，自然圖像通常不是稀疏的，因此對圖像直接應用壓縮感知算法很難取得高壓縮效率.針對圖像信號，將編碼思想融入壓縮感知理論，提出一種簡單有效的零樹壓縮感知方法.該方法先利用零樹思想輔助壓縮感知測量，在得到測量值的同時編碼重要系數的位置；然后提出零樹追蹤重構算法，通過精確解碼重要系數位置來重構原始圖像小波系數，提高重構精度.實驗結果表明，相比于現有匹配追蹤算法和EZW算法，本文方法有更高的壓縮比和更好的圖像重構質量.

關鍵詞：小波變換；圖像處理；壓縮感知；編碼

中圖分類號：TP37 文獻標志碼：A

Image Zerotree Compressed Sensing

Based on Wavelet Transform

ZHOU Siwang，LIU Longkang

（College of Information Science and Engineering，Hunan University， Changsha 410082，China）

Abstract：The basic principle of Compressed Sensing （CS） theory is that if a signal is sparse， CS promises to deliver a full recovery of this signal with high probability from far fewer measurements than the original signal. Unfortunately， image signals usually are not sparse， and thus it is difficult to obtain high compression performance for image compressed sensing.This paper proposed a simple and efficient zerotree compressed sensing method for images. In the proposed scheme， the classical zerotree coding is integrated into the process of measure to encode the precise locations of significant elements， which is used to restore the original image by the proposed pursuit reconstruction algorithm to improve the quality of the reconstructed image. The experimental results show that， compared with the existing matching pursuit algorithms and Embedded Zerotree Wavelet （EZW） coding algorithm， the proposed algorithm achieves much higher compression ratio and better image quality.

Key words：wavelet transform；image processing； compressed sensing； encoding

小波變換是圖像壓縮的重要方法[1].當圖像信號經由小波變換轉換到小波域后，其小波域系數隱含多分辨的樹結構，存在相關性.在圖像的小波域系數中，如果父系數小于給定的閾值，則其子系數也很大概率小于此閾值，利用此相關性對小波系數做進一步的編碼，可顯著增加圖像壓縮性能.嵌入式小波零樹編碼（EZW）[2]是最經典的一種圖像編碼方法，通過設計正重要系數、負重要系數、孤立零和零樹根，將小于閾值的父子小波系數組織成樹結構，提高了圖像壓縮比.

Donoho等[3-5]認為，上述傳統變換壓縮方法魯棒性差，而且壓縮效率存在“自適應”的特點并且依賴信號本身的結構，進而提出了一種稱為“壓縮感知”的新理論，近年來吸引了越來越多研究人員的關注.設長度為N的信號x滿足K-sparse特性，即x中僅有K（KN）個元素為非零，則可由M×N（MN）大小的測量矩陣φ將信號x投影到低維空間，得到測量值y：y=φx.通過求解最優化問題：min ‖x‖0s. t . φx=y 即可以由φ和投影測量值y高概率地重構出原始信號，其中‖x‖0表示信號x的0范數.因為M遠小于N，信號無需編碼即被壓縮.研究表明，上述最優化問題的求解可以轉化為線性規劃問題.Tropp等人[6]提出利用正交匹配追蹤（OMP） 算法來重構信號，大大提高了計算的速度，且易于實現.OMP算法的本質是在K-sparse信號x中尋找關鍵的K個分量.其基本思想是比較測量矩陣φ的每一個列向量與測量值y的內積，每次追蹤時確定1個關鍵分量的位置，并用最小二乘法求解此分量的值，直至找到K個關鍵的分量，從而重構出原始信號.Donoho等人[7-8]進一步提出了分段正交匹配追蹤（StOMP）算法和壓縮采樣匹配追蹤 （CoSaMP）算法，加快了圖像重構的速度.

信號的稀疏性是實現OMP等壓縮感知算法的前提.不幸的是，一般來說圖像是非稀疏的二維信號，通常的做法是將圖像轉換為某種變換域，例如小波域，然后再做壓縮感知測量[9-10].當圖像轉換為小波域后，幅值大的小波系數主要聚集在低頻子帶，而高頻子帶的小波系數幅值大多接近于零，具有近似稀疏的特點.圖像經多級小波變換后，各子帶的小波系數形成層次結構，呈現出父子對應關系.每個父系數有4個子系數；每個子系數像他們的父系數一樣，又有4個子系數，依次類推.父子小波系數之間存在時空相關性，一般來說，如果父系數的幅值小，則子系數有很大概率也是小系數.Donoho等人[11]提出多尺度壓縮感知 （MCS）算法，對圖像小波域的低頻子帶采用線性傳遞，而對高頻子帶則按不同的變換級分別進行壓縮感知測量，再利用OMP等算法重構原始圖像.MCS算法不拘泥于經典壓縮感知理論，它根據圖像小波域子帶的特征融合壓縮感知和線性測量兩種方法，獲得了好的圖像重構質量.值得注意的是，Baraniuk等人[12]的研究表明，如果能利用圖像小波域系數層次結構所展示的相關性來設計重構算法，則能進一步提高重構精度.壓縮感知重構的效率依賴于信號的稀疏性特征，然而，即使將圖像變換到小波域，也僅是近似稀疏的.對OMP等現有壓縮感知算法來說，若想獲得高的圖像重構精度，只能大幅度增加測量次數，從而造成壓縮比下降.針對此問題，我們認為僅僅對圖像進行壓縮感知是不夠的.

據此，本文將傳統數據壓縮的編碼思想融入壓縮感知的測量步和重構步，提出一種基于圖像小波變換的零樹壓縮感知方法，利用小波系數的相關性來提高圖像重構質量和壓縮比.

1 基于小波變換的零樹壓縮感知方法

本節首先介紹零樹的定義，然后將零樹的思想融入壓縮感知理論，提出基于圖像小波變換的零樹壓縮感知方法，包括基于小波零樹的測量算法和零樹匹配追蹤重構算法兩部分.測量算法在測量步運行，圖像被壓縮；重構算法在重構步運行，圖像被恢復.

1.1 零樹和零樹根

文獻[2]中定義了零樹根和零樹的概念.

定義1（零樹根） 在圖像小波域中，對于一個值為零的小波系數，如果它的父系數是重要系數，而子孫系數均為零，則稱之為零樹根.

定義2（零樹） 零樹根和它的子孫系數稱為零樹.

零樹體現了小波系數的相關性.已知初始閾值，若小波系數的絕對值大于該閾值，則稱之為重要系數，反之則是不重要系數.在對圖像進行多級小波變換后，小波系數呈現出相互關聯的統計特性.若父系數是不重要系數，則其子孫有很大概率也是不重要系數.零樹即是利用這種特性定義的一種數據結構.文獻[2]基于零樹設計一種稱為EZW的編碼算法，實現了圖像壓縮.

本文將對零樹編碼加以改造，使之與壓縮感知理論相融合，進而提出一種新的零樹壓縮感知方法.

1.2 基于小波零樹的測量算法

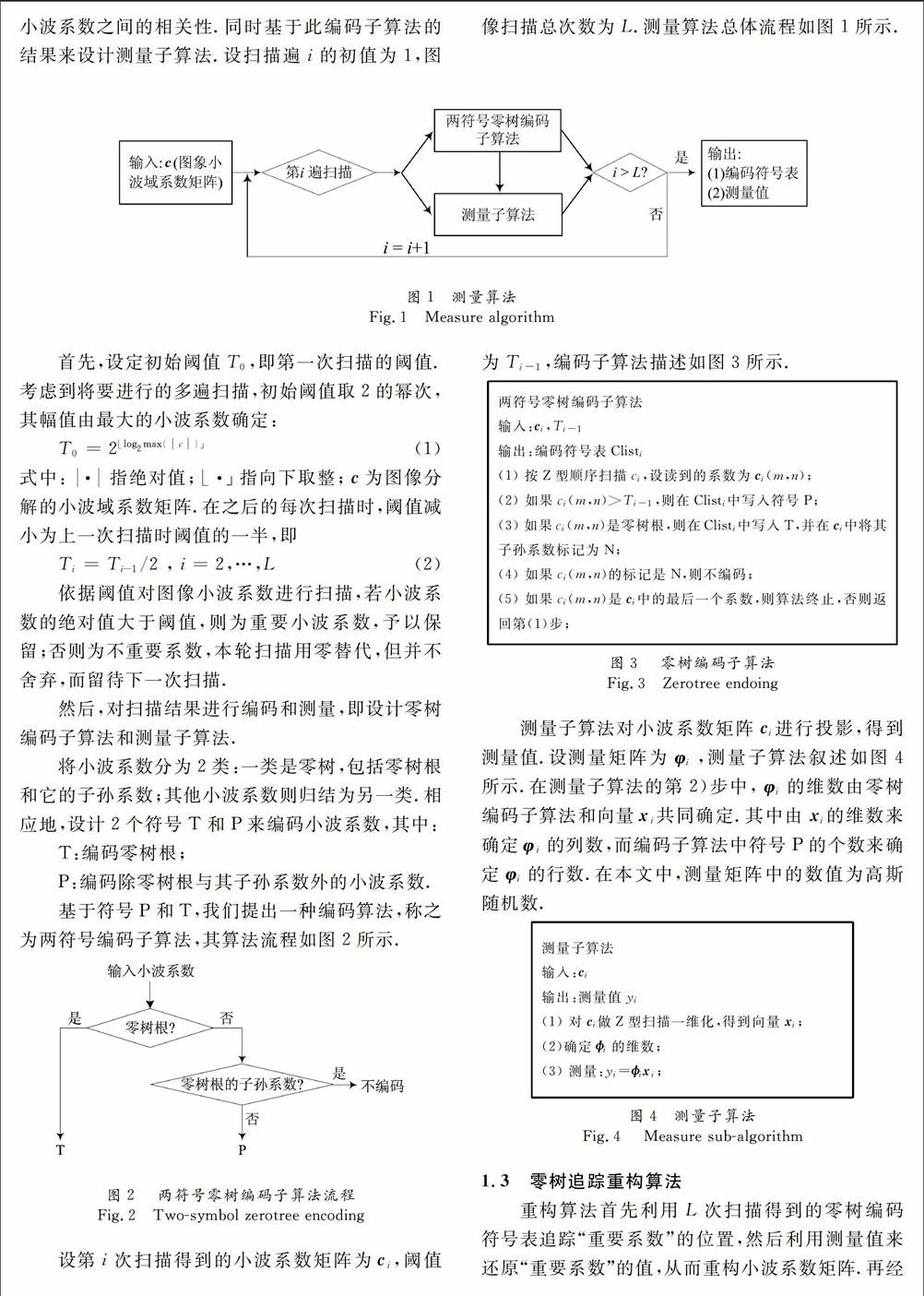
測量算法的核心是兩符號零樹編碼子算法和測量子算法.在兩符號零樹編碼子算法中，我們設計兩個符號T和P來編碼小波系數，基于零樹挖掘多級小波系數之間的相關性.同時基于此編碼子算法的結果來設計測量子算法.設掃描遍i的初值為1，圖像掃描總次數為L.測量算法總體流程如圖1所示.

測量子算法對小波系數矩陣ci進行投影，得到測量值.設測量矩陣為φi，測量子算法敘述如圖4所示.在測量子算法的第2）步中，φi的維數由零樹編碼子算法和向量xi共同確定.其中由xi的維數來確定φi的列數，而編碼子算法中符號P的個數來確定φi的行數.在本文中，測量矩陣中的數值為高斯隨機數.

1.3 零樹追蹤重構算法

重構算法首先利用L次掃描得到的零樹編碼符號表追蹤“重要系數”的位置，然后利用測量值來還原“重要系數”的值，從而重構小波系數矩陣.再經過小波逆變換重構原始圖像.零樹追蹤算法的輸入是包括L個編碼符號表和L組測量值.由圖3和圖4不難看出，這正是測量算法的輸出.

設原始圖像的大小為M×N，算法描述如圖5所示.

從圖5所示的算法描述來看，零樹追蹤重構算法分為2個階段，第1個階段是追蹤重要系數的位置，即符號P的位置，并依據P的位置確定測量

矩陣φi用于重構的支撐集合，即φP.第2個階段是用最小二乘法還原小波系數x′i，即使用公式x′i=（φTPiφPi）-1φTPiyi求解x′i.

性質 零樹追蹤重構算法具有嵌入式特征.

從圖5所述零樹追蹤算法的第（2）步（for循環步）可以看出，我們提出的重構算法分為L小步，每一步重構出一部分小波系數xi'.隨著重構步數向L步逼近，矩陣C與原始圖像小波系數矩陣的距離越來越小.也就是說，對C做小波逆變換，得到重構圖像的誤差越來越小，即具有嵌入式重構的特征.

具有嵌入式特征的零樹追蹤算法魯棒性強，在此L小步循環中的任意步退出循環，算法依然能夠正常重構，得到相應精度的重構圖像，循環的次數越多，圖像重構的精度就越高.

1.4 復雜度分析與示例

本小節先從計算復雜度的角度對小波零樹壓縮感知方法做簡要分析，然后以一個8×8的數據矩陣為例，給出算法運行的示例.

我們提出的零樹壓縮感知方法包括測量算法和重構算法.測量算法的核心是兩符號零樹編碼子算法和測量子算法.編碼子算法需要對圖像的小波變換系數進行遍歷，設圖像的大小為n（n=M×N），則第i次掃描時編碼子算法的計算復雜度為O（n）；設第i次掃描時得到符號P的個數為pi，L遍掃描得到的大系數總數為p，即p=∑Li=1pi.這樣，測量子算法的計算復雜度為O（pin），則總的測量復雜度為O（Ln）+O（pn）.因為L為預先設定的常數，所以，測量算法的復雜度可以控制在O（pn）以內.重構算法包括還原大系數位置和計算大系數的值.其中，還原大系數位置所需復雜度為O（Ln）；每遍掃描計算大系數值需要O（p2in）次操作，共需計算L遍，復雜度為O（Ln+∑Li=1p2in）.因此，重構算法的總重構復雜度為O（p2n）.考慮到所有壓縮感知算法均需測量矩陣，因而在上述分析中，我們沒有考慮生成測量矩陣φ的復雜度.

接下來，針對一幅8×8的圖像經過3級分解后得到的小波系數矩陣（如圖6所示），以一次Z型掃描為例（即L=1），給出一個算法實現的示例.

然后運行重構算法.重構算法的輸入是測量算法的輸出，也就是說，輸入是Clist1和y1.先由Clist1恢復出大系數的位置，得到矩陣C1，如圖8所示.

依據C1中符號P的位置和矩陣φ1確定矩陣φp1，再由公式x′1=（φTP1φP1）-1φTP1y1計算出重構向量x′1，并按Z型掃描順序回寫入矩陣C.從圖9可以看出，矩陣C和圖7所示結果一致，表明完全重構了第1次掃描結果.隨著掃描級數的增加，矩陣C中的空白元素逐漸被填滿，最終還原出如圖8所示的小波系數矩陣.

1.5 討 論

在OMP，StoMP和CosaMP等經典壓縮感知重構算法中，追蹤重要系數的位置帶來了很大的計算復雜度，而且因此引起的位置誤差造成重構精度嚴重下降.本文的基本思路是利用編碼思想來精確追蹤重要系數的位置，然后再基于最小二乘重構重要系數的值，從而提高重構精度.

在測量算法中，編碼的目的是追蹤重要系數的位置，而無需如EZW算法一樣編碼重要系數的值，因此我們只簡潔地設計了兩個符號P和T，既能充分利用小波系數相關性，又能提高壓縮比.然而在該子算法中，除零樹根和相應的零樹元素外的其他系數均被編碼成P.這造成我們將孤立的零系數也看成了重要系數，帶來了額外的計算開銷.但因為小波相關性的緣故，這樣的思路不會影響到算法的效率，我們將在實驗部分加以驗證.

多遍掃描提高了稀疏度，也使得我們的方法具有魯棒性.圖像的小波域系數不是嚴格的稀疏信號，通過多遍掃描，不僅提高了每一次參與壓縮感知的子信號稀疏度，而且，多遍掃描具有嵌入式特點，即便是算法意外終止，也會獲得相應精度的重構圖像，具有魯棒性.

2 實驗與分析

本節測試小波圖像零樹壓縮感知方法的性能，并與OMP，StOMP和CoSaMP等壓縮感知算法以及EZW等編碼壓縮算法進行對比.實驗的硬件環境是配置Intel（R） Xeon（r） E4028 四核 2.0 GHz CPU和4 G內存的PC機，軟件環境是Windows7和Matlab 7.0.選取128×128大小的Lena，Shepp-Logan Phantom和Mondrian圖像進行測試.這3個圖像具有很好的代表性，標準測試圖像Lena是平滑的自然圖像，Mondrian屬于簡單圖像，而Shepp-Logan Phantom則是介于兩者之間的醫學圖像.在實驗中，對上述3種圖像信號采用Daubechies 9/7進行3層小波分解.

本實驗的評價指標是運行時間t，壓縮比CR和峰值信噪比PSNR.運行時間t用于評估算法的計算復雜度.圖像壓縮比CR用于評價測量與編碼算法的壓縮效率，定義為原始圖像的數據量Data_image與傳輸數據量Data_trans的比值.傳輸數據量即測量算法輸出到重構算法的數據量.CR用公式表示如下：

CR=Data_imageData_trans （3）

PSNR則用于評價重構算法恢復圖像的精度.對于大小為M×N的圖像，PSNR定義為：

PSNR=10log 25521M×N∑M-1m=0∑N-1n=0（Xmn-mn）2 （4）

式中：mn為重構圖像第m行n列的灰度值；Xmn為原始圖像第m行n列的灰度值；M×N為圖像像素個數.

圖10給出了在傳輸數據量相同的情況下，Lena，Shepp-Logan Phantom和Mondrian等 3類圖像信號在不同方法下重構的視覺效果.其中Lena圖像，Shepp-Logan Phantom圖像和Mondrian圖像的數據傳輸量分別為9 060字節，6 460字節和5 020字節，相應的壓縮比分別為1.8，2.5和3.3.從視覺效果看，本文提出的小波圖像零樹壓縮感知方法遠優于OMP算法，同時也好于EZW算法.然而，和原始圖像相比，Lena圖像的視覺效果還不能滿足人們對圖像質量的需求.壓縮感知理論將采樣和壓縮結合起來，提高了壓縮成像的速度，但要將其應用于自然圖像壓縮，還需更加深入的研究.

在相同的傳輸數據量下，圖11和圖12分別比較了各算法的圖像重構質量和運行時間.在本實驗中，我們用運行時間來評估算法的計算復雜度.從圖11可以看出，在重構質量方面，小波零樹壓縮感知方法優于OMP，StOMP，CoSaMP以及EZW算法，究其原因，是因為我們提出的重構算法通過解碼可以精確恢復出大系數的位置，而且，只要采樣次數等于符號P的個數，就能完全重構出大系數的值.從圖12可以看出，我們提出的重構算法運行時間少于OMP算法；對于Shepp-Logan Phantom圖像，本文方法的運行時間與StOMP，CoSaMP以及EZW算法相當，而對于Mondrian和Lena圖像，則要花費更長的運行時間.這是因為相比于OMP算法，本文方法無需逐個追蹤重要系數，因而降低了復雜度，節省了運行時間.然而，本文方法需要解碼和重構兩個過程，相應地帶來了額外的時間開銷.

圖13比較了各種方法的壓縮效率.可以看出，我們提出的小波零樹壓縮感知方法比其他方法有更高的壓縮比.和EZW算法相比，本文方法采用簡潔的兩字符零樹編碼，這樣，后續的算術熵編碼有更高的效率，因而有更高的壓縮比.和OMP，StOMP和CoSaMP等算法相比，本文方法編碼了大系數的位置，因而測量次數顯著減少.特別是在低重構精度的前提下，本文方法的壓縮比遠大于其他算法.

圖14給出了在圖像重構質量相同的情況下，各壓縮感知測量算法消耗緩存的對比結果.可以看出，相對于OMP，StOMP和CoSaMP等壓縮感知匹配追蹤算法，本文方法有最少的緩存數據量.這是因為在我們提出的測量算法中，零樹編碼子算法精確編碼了重要系數的位置，因此重構算法可以據此重構重要系數的值.這樣，測量矩陣φi的行數就會大大減少，因此比其他算法節省了更多的緩存.

3 結 論

圖像的小波域系數不是嚴格稀疏的，因此匹配追蹤等壓縮感知重構算法很難正確追蹤重要系數的位置，從而降低了圖像壓縮感知的效率.鑒于此，本文將編碼思想融入壓縮感知的測量步與重構步，提出了一種基于圖像小波變換的零樹壓縮感知方法，包括兩符號零樹編碼子算法、測量子算法和零樹追蹤重構算法等.針對Lena，Shepp-Logan Phantom和Mondrian等3類測試圖像的實驗結果表明，在重構時間方面，本文方法的運行時間優于OMP算法；在壓縮效率方面，本文方法的壓縮比遠高于OMP，StOMP和CoSaMP等匹配追蹤算法以及EZW編碼壓縮算法；在重構質量方面，本文方法也有最好的圖像恢復精度；同時，本文方法也比OMP，StOMP，CoSaMP等算法消耗更少的緩存.

本文提出的零樹壓縮感知方法具有嵌入式特征，如何利用它來提高順序壓縮感知算法[13]的效率是我們將要進行的下一步工作.

參考文獻

[1] DAUBECHIES I. Ten lectures on wavelets [M]. Philadelphia： SLAM，1992： 105-108.

[2] SHAPIRO J M.Embedded image coding using zero trees of wavelet coefficients[J]. IEEE Transaction on Signal Processing， 1993， 41（12）： 3446-3462.

[3] DONOHO D. Compressing sensing [J]. IEEE Transactions on Information Theory， 2006， 52（4）： 1289-1306.

[4] 羅琦，魏倩，繆昕杰.基于壓縮感知思想的圖像分塊壓縮與重構方法[J].中國科學：信息科學， 2014， 44（8）： 1036-1047.

LUO Qi，WEI Qian，MIAO Xinjie. Blocked image compression and reconstruction algorithm based on compressed sensing[J]. Science China： Information Science， 2014， 44（8）： 1036-1047.（In Chinese）

[5] 吳光文，張愛軍，王昌明.一種用于壓縮感知理論的投影矩陣優化算法[J].電子與信息學報，2015，37（7）：1681-1687.

WU Guangwen，ZHANG Aijun，WANG Changming.Novel optimization method for projection matrix in compress sensing theory[J].Journal of Electronics & Information Technology，2015，37（7）：1681-1687.（In Chinese）

[6] TROPP J，GILBERT A.Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transaction on Information Theory， 2007， 53（12）： 4655-4666.

[7] DONOHO D L，TSAIG Y，DRORI I，et al.Sparse solution of underdetermined systems of linear equations by stagewise orthogonal matching pursuit[J]. IEEE Transaction on Information Theory， 2012， 58（2）： 1094-1121.

[8] NEEDELL D，VERSHYNIN R.Signal recovery from incomplete and inaccurate measurements via regularized orthogonal matching pursuit[J]. IEEE Journal of Selected Topics in Signal Processing， 2010， 4（2）： 310-316.

[9] 周四望，羅夢儒.順序小波包圖像壓縮感知方法[J].湖南大學學報：自然科學版，2015，42（4）：130-135.

ZHOU Siwang，LUO Mengru.Sequential image compressed sensing based on wavelet packet[J].Journal of Hunan University： Natural Sciences， 2015， 42（4）： 130-135.（In Chinese）

[10]HOU Y，ZHANG Y. Effective image block compressed sensing with quantized measurement[C]//IEEE Data Compression Conference.Snowbird： IEEE Computer Society，2014： 407-411.

[11]DONOHO D L，TSAIG Y.Extensions of compressed sensing[J].Signal Processing， 2006， 86（3）： 533-548.

[12]BARANIUK R，CEVHER V，DUARTEM ，et al.Model-based compressive sensing[J].IEEE Transactions on Information Theory， 2010， 56（4）： 1982-2001.

[13]WEI D，HERO A O.Multistage adaptive estimation of sparse signals[J]. IEEE Journal of Selected Topics in Signal Processing， 2013， 7（5）：783-796.