一種改進的線性分組碼的全盲識別算法
王蘭勛,賈層娟,郭淑婷
(河北大學 電子信息工程學院,河北 保定 071002)
一種改進的線性分組碼的全盲識別算法
王蘭勛,賈層娟,郭淑婷
(河北大學 電子信息工程學院,河北 保定 071002)
針對線性分組碼編碼參數的盲識別問題,根據實際與隨機序列碼重概率分布間較大的差異性,提出了利用兩種特征參數(碼重標準差率差值、碼重信息熵)分別同時識別碼長和起始點的算法。根據這兩種算法的不足又進一步改進,提出一種對這兩種特征參數進行融合來同時識別碼長和起始點的算法。在此基礎上,通過建立矩陣進行化簡獲得生成矩陣,從而實現線性分組碼的全盲識別。理論分析及實驗仿真表明該方法簡單易行,容錯性較強,在誤碼率為0.025條件下對中短碼識別率達到90%,誤碼率為0.005條件下對中長碼識別率高于80%。
線性分組碼;全盲識別;碼重標準差率差值;特征參數融合
信道編碼盲識別技術可以在所接收編碼信息不全的條件下對線性分組碼進行盲識別。在通信領域中,信道編碼盲識別應用范圍較廣,它可以在衛星通信、非協作通信等領域對信息進行盲識別,因此具有重要的研究意義[1-3]。
本文針對線性分組碼盲識別問題展開研究,但據已有公開發表的文獻可知,目前針對線性分組碼的全盲識別的研究相對較少。文獻[4]利用比特頻率檢測法估計碼長和碼字同步點,只適用于較低誤碼環境,且容錯性一般。文獻[5]基于碼重相似度算法識別碼長和碼字起始點,只適用于一種先驗條件已知的情況,且容錯性也一般。文獻[6]利用矩陣秩信息熵及碼重信息熵分別識別碼長和碼字起始點,但需要多次構造矩陣,比較復雜。文獻[7]利用碼重信息熵識別碼長,雖適用于較高誤碼環境,但需已知同步點。文獻[8]根據矩陣變換和碼重分布來識別碼長和起始點,但容錯性一般。文獻[9]利用碼重分布概率方差識別碼長,雖然運算量較小,但需要已知同步點。文獻[10]利用碼重分布距離識別碼長和碼字起始點,只適用于較低誤碼的環境。文獻[11]根據解調輸出的軟判決序列求解有錯的方程,但運算量所需較大。文獻[12]利用“3倍標準差”準則和判斷對偶空間歸一化維數的最大值來識別碼長和碼字起始點,但計算量較大。
基于以上分析,上述識別方法中有些容錯性一般或者只適用于較低誤碼環境,有些是必須在碼字起始點(碼字同步點)已知的條件下才能完成識別,而不能實現全盲識別。為此,本文提出利用碼重標準差率差值與碼重信息熵進行融合來同時識別碼長和起始點的算法,該算法可以實現線性分組碼的全盲識別。
1 線性分組碼識別基礎
定義1[13]:一個(n,k)分組碼的基本單位是碼字,每個碼字是由k個信息位和n-k個監督位組成,如果它的信息位和監督位之間是一種線性的代數關系,則稱為線性分組碼。
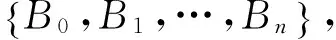
定義3[15]:q元[n,k]線性分組碼是GF(q)上的n維線性空間Vn中的一個k維子空間Vn,k,設C是一個q元[n,k]線性分組碼,將C的一組基底作為行向量構成一個k×n階矩陣G,那么G就是線性碼C的生成矩陣。將具有[IkP]形式的G矩陣稱為典型陣。
定理[13](n,k)線性分組碼的k位信息生成的n位碼字集v是n維向量空間V的子集,且v在V中的分布一定是非等概的。
2 兩種特征參數識別方法
2.1 兩種算法描述
對于(n,k)線性分組碼而言,碼組內各碼元之間具有較強的完整的線性約束關系,且不同碼重的碼組分布是非等概的,而隨機序列隨機性比較大,所以不具有較強的線性約束關系,導致碼重分布不平衡。根據實際序列和隨機序列碼重分布概率之間的差異最大這一特性,利用碼重標準差率差值、碼重信息熵兩種特征參數來分別對線性分組碼進行全盲識別。
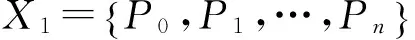
1)碼重標準差率差值
定義:實際序列的碼重分布概率的CV與隨機序列的碼重分布概率的CV的差值定義為碼重標準差率差值,即
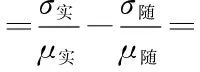
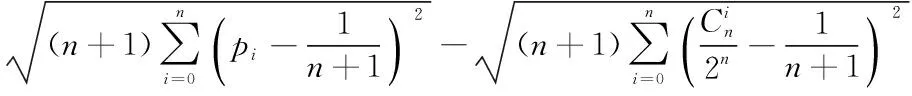
(1)
其中:σ實,σ隨表示X1,X2的標準差;μ實,μ隨表示X1,X2的均值;CV表示概率分布的離散程度。對于真實序列,碼重分布相對集中,即CV較大;對于隨機序列,碼重分布相對分散,即CV較小。故當遍歷到真實的碼長和起始點時,真實序列的碼重分布概率相對于隨機序列較集中,且與隨機序列的分布特性相差較大,ΔCV最大。因此當標準差率差值ΔCV最大時,識別出真實的碼長和起始點。
2)碼重信息熵
定義信息熵函數為
(2)
上述已介紹物理量pi(pi≠0)。經上述分析知線性分組碼的碼重分布不平衡,其碼重分布概率與隨機序列的碼重分布概率之間的差異性很大,當遍歷到真實的碼長和起始點時,實際序列具有較強的非隨機性,導致碼重分布不平衡,與隨機序列相差較大,因此當Hn最小時,識別出真實的碼長和起始點。
2.2 識別方法的步驟
假設接收序列長度為R,則識別碼長、起始點的步驟概括如下:
1)初始化待識別參數:碼長為n,n取值范圍是3~l,l是指最大可能碼長;起始點為m,m取值范圍是1~n+1。
2)將截獲的實際序列以起始點m開始,按碼長n劃分為Ω個碼字,在每種(n,m)下假設待測矩陣為XΩ×n(n,m)=(x1+(Ω-c)n,x2+(Ω-c)n,…,xn+(Ω-c)n),其中:c=Ω,Ω-1,…,1。
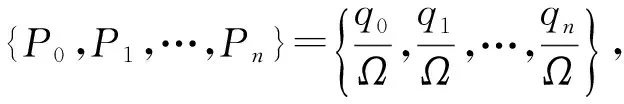
4)求出每種假設(n,m)下的實際序列與隨機序列的碼重分布概率,利用式(1)、式(2)分別求ΔCV、Hn的值,找出ΔCV最大和Hn最小時對應的(n,m)即為真實的碼長和起始點。
2.3 仿真驗證及分析
選取(15,5)線性分組碼為研究對象,參數設置如下:碼組個數為1 000組,誤碼率為Pe=0.02,起始點設為6。根據2.2節識別步驟,基于ΔCV、Hn兩種特征參數的算法的識別仿真結果如圖1和圖2所示。
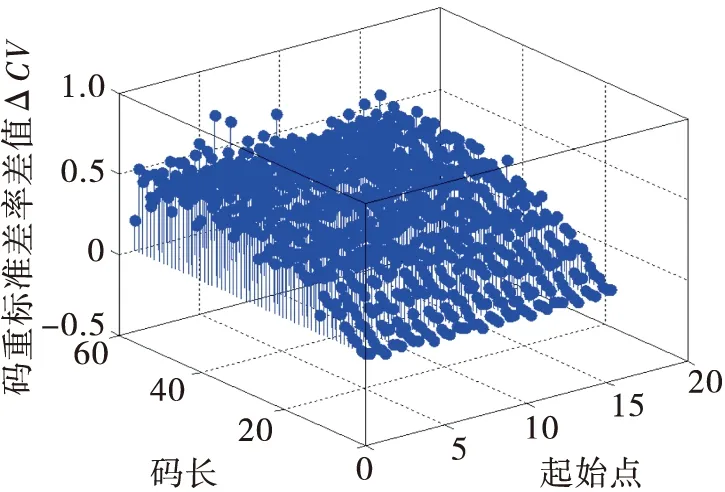
圖1 基于ΔCV全盲識別仿真圖
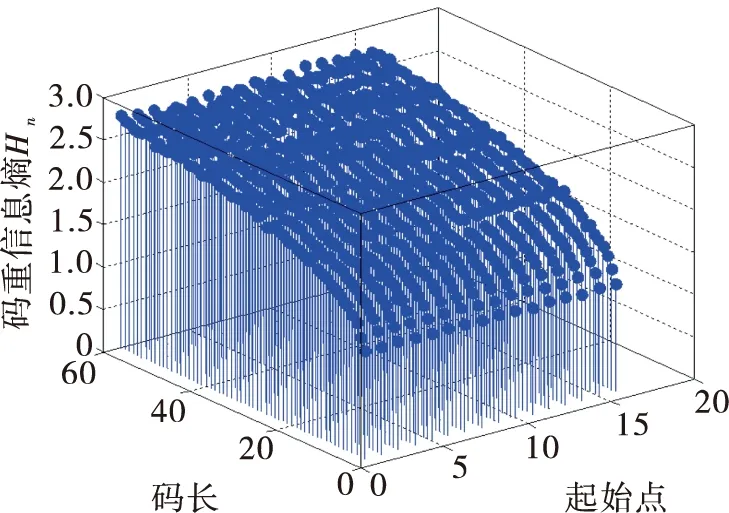
圖2 基于Hn全盲識別仿真圖
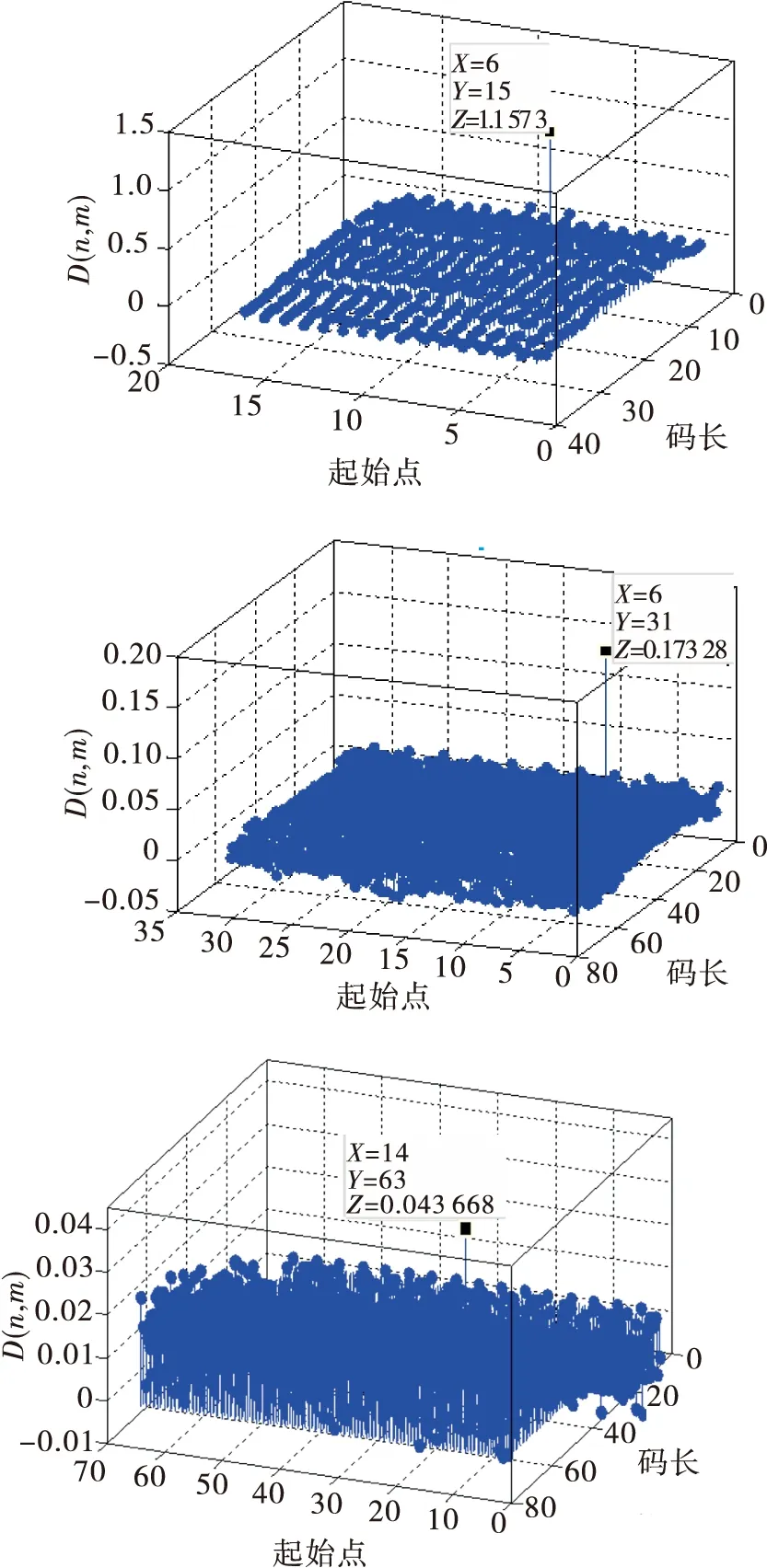
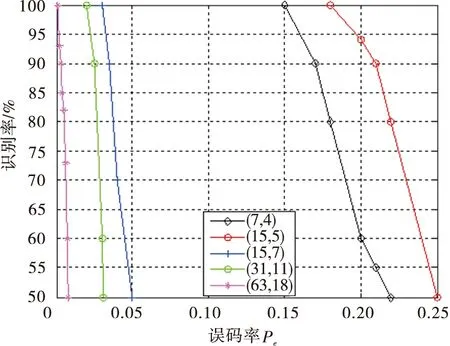
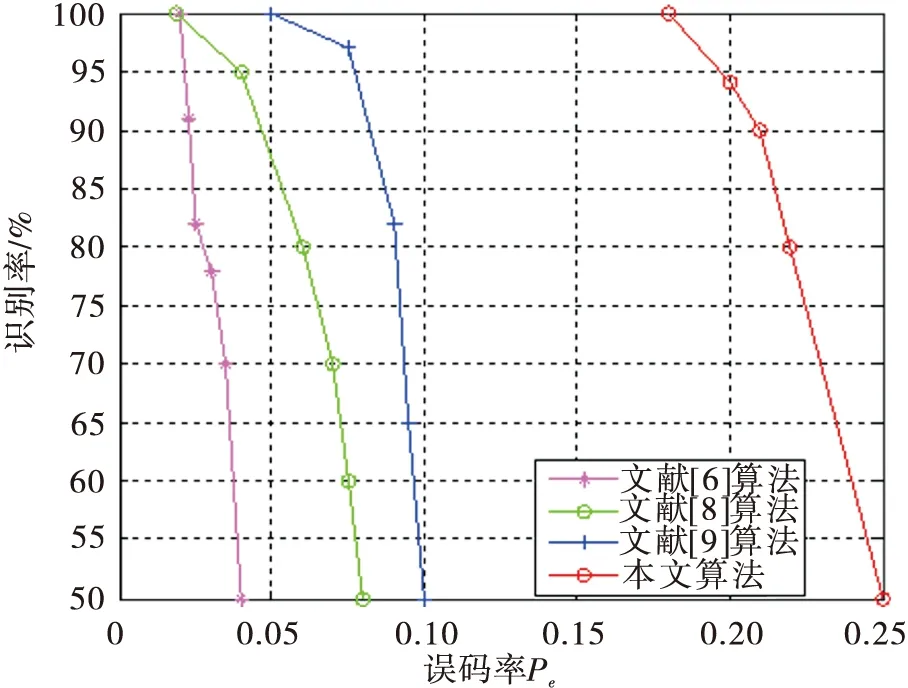
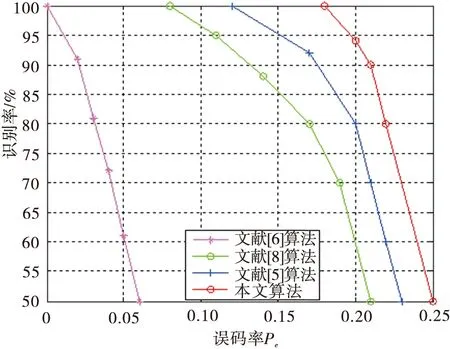
從圖2中不易清晰地觀察出4×4的最小值,所以對式(2)進行改進,對I2取負值,使得碼重信息熵最大時識別出真實的碼長和起始點。由圖2可知0 (3) 根據2.2節識別步驟,基于Sn的仿真結果如圖3所示。 圖3 基于Sn全盲識別仿真圖 經分析可知,碼重標準差率差值ΔCV與碼重信息熵Sn是衡量對象之間的差異程度,取值最大時,則實際序列和隨機序列的差異性較大,此時最大值即為真實的碼長和起始點。由圖1、圖3可知,由于ΔCV與Sn的各個值之間相差范圍較小,變化不明顯并且不易區分,所以不易實現全盲識別。因此,對這兩種特征參數進行融合使變化范圍較明顯,從而實現全盲識別。 3.1 融合算法描述 通過上一章節對兩種特征參數的仿真驗證,由圖1、圖3可知,最大值都不能在仿真圖中明顯看出,并且它們的值的分布都形似坡狀。圖1較小值分布在碼長為(20,40)的范圍內,較大值分布在(40,60)的范圍內。而圖3較小值分布在碼長為(40,60)的范圍內,較大值分布在(20,40)的范圍內。由于它們較小值與較大值分布范圍正好相反,為此本文利用兩種特征參數進行相乘,即ΔCV×Sn,使得較小值與較大值相乘后較大值取值變小,而最大值與最大值相乘后使得最大值更加突顯,以致于差異明顯增大,且仿真圖中可以明顯看出最大值的位置,從而實現全盲識別。由此,兩種特征參數融合的公式為 D=ΔCV×Sn (4) 將式(1)和式(3)代入式(4)可得 (5) 融合特征參數即融合了概率分布的碼重標準差率差值和碼重信息熵,根據上述對兩種特征參數的理論分析,知當D最大時識別出真實的碼長和起始點。 3.2 識別方法的步驟 同上章2.2節的識別步驟,將步驟(4)中的公式換成式(5)。 3.3 仿真驗證及分析 本次實驗選取誤碼率為Pe=0.02的(15,5),Pe=0.01的(31,11)線性分組碼,起始點設為6,及Pe=0.003的(63,18)線性分組碼,起始點均設為14,碼組個數均為1 000組,利用MATLAB進行仿真實驗,識別結果如圖4所示。 圖4 全盲識別仿真曲線圖 由圖4三維圖可看出,坐標位置分別在(15,6),(31,6),(63,14)處函數值D取得最大值,可知該處的坐標值即為碼長和碼字起始點的真實值。對于上述3種線性分組碼,雖誤碼率不同,但都能較明顯地識別出碼長和起始點。經分析知,當碼長和起始點為真實值時,碼組內具有完整的線性約束關系,實際序列的碼重分布概率是非等概的,導致碼重分布不平衡,與隨機序列的碼重分布概率差異性最大,使得融合特征參數D值變化最大,所以D值最大時所對應的為真實的碼長和起始點。經仿真驗證該算法在一定的誤碼率條件下可以實現對碼長和起始點的全盲識別,且識別效果明顯。 4.1 理論描述及分析 (6) 式中:Gk×n即為線性分組碼的生成矩陣。 為達到無錯誤碼字最大化進行多次化簡計算,選取出現概率最大的一組最大線性無關向量組排列成矩陣進行化簡,即完成生成矩陣的識別。 4.2 仿真驗證及分析 (7) 對于不同參數的線性分組碼,選取(7,4),(15,5),(15,7),(31,11),(63,18)5種線性分組碼為研究對象來討論該融合識別方法的容錯性能。在不同誤碼率下對不同碼長均取1 000組碼字,進行500次蒙特卡洛仿真實驗,運用融合特征參數統計不同誤碼率下的正確識別率,識別率曲線圖如圖5所示。 圖5 全盲識別概率曲線圖 由圖5可看出,(7,4)在高誤碼率為0.17時,識別率達到90%;(15,5)在高誤碼率為0.21時,識別率達到90%;(15,7)在誤碼率為0.035時,識別率達到90%;(31,11)在誤碼率為0.025時,識別率達到90%;(63,18)在誤碼率為0.005時,識別率高達80%以上。由圖可知,對于(15,5)與(15,7)兩種碼字,隨著誤碼率的增加,前者識別率高于后者,可以看出碼長相同、碼率不同時,低碼率碼字識別效果較好。因此從上述分析可以得出,隨著誤碼率、碼長和碼率的逐漸增大,碼組內碼字之間的線性約束關系逐漸減弱,使得識別率降低,可見,該識別算法在誤碼率為0.005條件下,可以有效地實現中長碼的全盲識別。 以(15,5)線性分組碼作為研究對象,在碼字種類和碼組個數相同的條件下,對文獻[5-6,8-9]和本文算法分別進行500次蒙特卡洛仿真實驗。圖6為本文算法與文獻[6,8-9]碼長識別率進行比較,可以看出本文算法在高誤碼率為0.21時的碼長識別概率高達90%,而其他3種算法均沒有本文算法容錯性好。圖7為本文算法與文獻[5-6,8]碼字起始點識別率進行比較,可以看出本文算法在高誤碼率為0.21時的碼字起始點識別概率達到90%,均優于其他3種算法。因此本文提出的對碼重標準差率差值和碼重信息熵進行融合來識別碼長和同步點的算法比以往算法更具有誤碼適應能力。 圖6 碼長識別率比較 圖7 同步點識別率比較 本文根據實際與隨機序列碼重概率分布之間的差異性特征,提出了基于碼重標準差率差值、碼重信息熵2種特征參數的算法分別同時識別碼長和起始點。但通過對2種特征參數的仿真驗證分析,發現這2種算法難以實現線性分組碼的全盲識別,進而提出了一種將碼重標準差率差值與碼重信息熵進行融合的全盲識別算法,可同時實現碼長與碼字同步點的識別。利用線性分組碼的特性,建立矩陣進行模二運算化簡識別生成矩陣,實現了線性分組碼的全盲識別。最后,進行仿真實驗,討論并分析其容錯性。結果表明,該算法簡單易懂,容錯性強于其他文獻,在高誤碼率為0.025情況下能有效地識別中短碼,在誤碼率為0.005情況下能有效地識別中長碼。 [1] 閆郁翰.信道編碼盲識別技術研究[D].西安:西安電子科技大學,2012. [2] 王蘭勛,熊政達,孫旭麗.本原BCH碼參數的盲識別方法[J].電視技術,2015,39(17):38-42. [3] 宋鏡業.信道編碼識別技術研究[D].西安:西安電子科技大學,2009. [4] 陳金杰,楊俊安.一種對線性分組碼編碼參數的盲識別方法[J].電路與系統學報,2013,18(2):248-254. [5] 王蘭勛,佟婧麗,孟祥雅.一種線性分組碼參數的盲識別方法[J].電視技術,2014,38(9):188-192. [6] 陳金杰,計同鐘,楊俊安.高誤碼條件下線性分組碼的盲識別[J].應用科學學報,2013,31(5):459-467. [7] 陳金杰,楊俊安.基于碼重信息熵低碼率線性分組碼的盲識別[J].電路與系統學報,2012,17(1):41-46. [8] 朱聯祥,李荔.改進的二進制循環碼盲識別方法[J].計算機應用,2013,33(10):2762-2764. [9] 鄭瑞瑞,汪立新.基于碼重分布概率方差的循環碼識別方法[J].太赫茲科學與電子信息學報,2013,11(5):792-796. [10] 王磊,胡以華,王勇,等.基于碼重分布的系統循環碼識別方法[J].計算機工程與應用,2012,48(7):150-153. [11] 于沛東,李靜,彭華.一種利用軟判決的信道編碼識別新算法[J].電子學報,2013,41(2):301-306. [12] 楊曉煒,甘露.基于Walsh-Hadamard變換的線性分組碼參數盲估計算法[J].電子與信息學報,2012,34(7):1642-1646. [13] 張永光,樓才義.信道編碼及其識別分析[M].北京:電子工業出版社,2010. [14] 趙曉群.現代編碼理論[M].武漢:華中科技大學出版社,2008. [15] 陳魯生,沈世鎰.編碼理論基礎[M].北京:高等教育出版社,2005. 王蘭勛(1956— ),教授,主要從事數字通信與信息編碼方面研究; 賈層娟(1988— ),女,碩士生,主研信道編碼盲識別; 郭淑婷(1992— ),女,碩士生,主研調制識別。 責任編輯:閆雯雯 Improved blind recognition method of linear block code parameters WANG Lanxun, JIA Cengjuan, GUO Shuting (CollegeofElectronicandInformationalEngineering,HebeiUniversity,HebeiBaoding071002,China) In view of the problem of the blind recognition of linear block code parameters, the code length and synchronization point are simultaneous identified by the recognition method based on the two characteristic parameter(standard error rate difference of code weight and information entropy of code weight)that is proposed by the difference of code weight distribution probability between the actual sequence and random sequence. According to the deficiency of these two algorithms, then a new method of fusion of two characteristic parameters is put forward that code length and synchronization point can be simultaneous identified. And through establishing matrix and simplifying Matrix, and identify the generator matrix to achieve a blind identification linear block codes.Theoretical analysis and simulation experience show that the recognition method is simple and has better error-tolerance, and the recognition method 90% with middle and short code length can be recognized when BER is 0.025 and has better performance more than 80% about slightly long code in 0.005BER. linear block code;blind recognition;standard error rate difference of code weight;characteristic parameter fusion 王蘭勛,賈層娟,郭淑婷.一種改進的線性分組碼的全盲識別算法[J].電視技術,2017,41(2):77-82. WANG L X, JIA C J, GUO S T. Improved blind recognition method of linear block code parameters [J]. Video engineering,2017,41(2):77-82. TP391 A 10.16280/j.videoe.2017.02.016 河北省自然科學基金項目(F2014201168) 2016-04-28
3 融合兩種特征參數識別方法
4 生成矩陣的識別
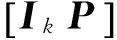
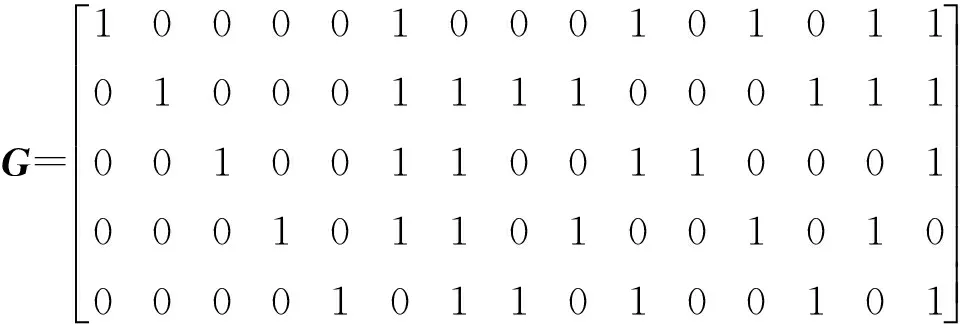
5 比較分析容錯性
6 結論

