高速多級離心泵轉軸系統橫向固有頻率分析

岳文超，吳敬東，王 典

?

高速多級離心泵轉軸系統橫向固有頻率分析

岳文超，吳敬東，王 典

（沈陽化工大學 能源與動力工程學院，遼寧 沈陽 110142）

將多級離心泵轉子簡化為受有軸向力的轉軸模型，用理論方法求解其橫向固有頻率；并應用有限元法，建立梁和質點單元的多級離心泵轉軸模型，對轉軸進行有預應力模態分析，求解轉軸的前五階彎振頻率，并利用鄧克萊法求得轉子模型的一階固有頻率，與有限元結果比較。結果表明軸向壓力使轉子系統固有頻率降低，軸向拉力使轉子系統固有頻率增加,且軸向力對轉子系統低階固有頻率影響較大，對高階頻率影響不顯著。

軸向力；固有頻率；模態分析；預應力

高速多級離心泵揚程高，工作可靠，成本低等優勢，廣泛應用于化工、冶金及工農業給排水行業中，為保證多級離心泵的平穩運轉，避免其在接近臨界轉速時發生共振而影響泵的正常運轉，對離心泵轉子橫向振動特性的研究是高速離心泵設計中重要的研究課題之一，國內外學者在此領域做了大量的研究工作[1-2]。在泵領域，孫興華[3]等對離心泵轉子進行了濕態臨界轉速以及邊界環境對其動力特性影響的研究，張和牧[4]等應用流固耦合的方法對水潤滑軸承的間隙做了優化設計，劉惠萍等應用流固耦合方法對軸承與轉子系統進行了油膜壓力與軸心軌跡的研究。目前在研究轉子系統的橫向振動時，不論是采用傳遞矩陣法還是有限元數值模擬，往往是不計軸向力的，這對于承受較大軸向力的轉軸，得出的結果會有不同程度的誤差。例如，在實際工程中，多級離心泵工作時，由于葉輪兩側壓力不等，將會承受巨大的軸向力作用，它將會對轉軸的臨界轉速產生影響。

本文通過理論方法和與數值模擬的方法，對加載軸向力的轉子系統橫向振動固有頻率進行求解和分析。對比了加載軸向力前后轉子系統的固有頻率，并分析軸向力對各階固有頻率的影響，為離心泵轉子系統的穩定可靠運行提供理論參考。

1 固有頻率的理論求解方法

1.1 具有軸向力的轉軸橫向固有頻率理論求解

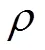
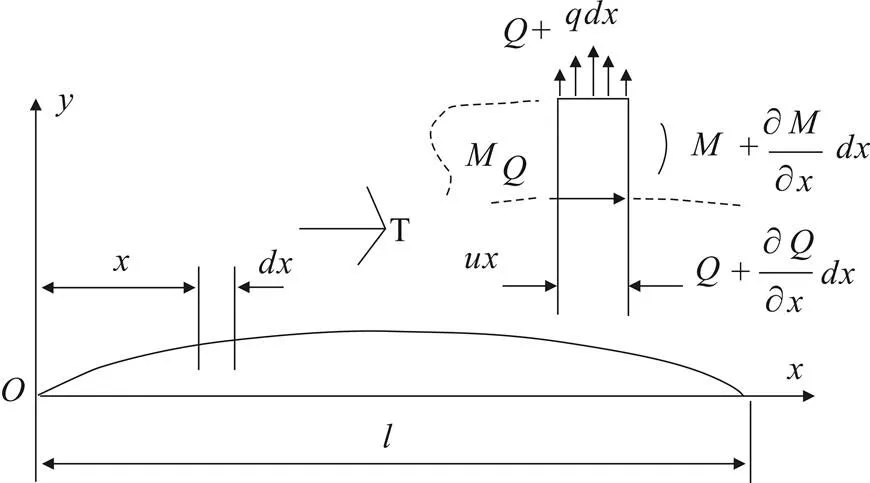
圖1 梁力學模型

當加載一軸向力時，軸在方向上的運動微分方程為

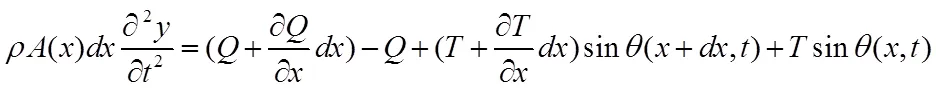
整理得

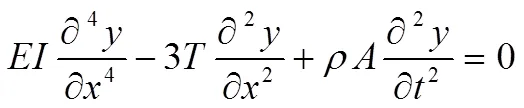
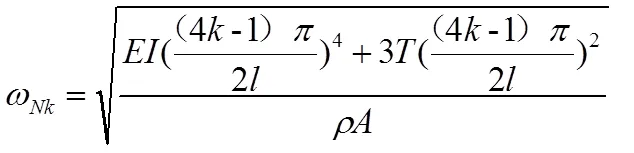
無軸力作用時的固有頻率為：

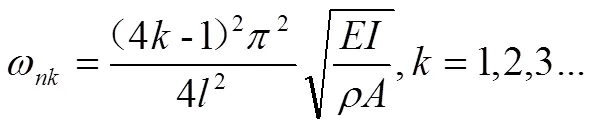
加載軸向拉力與無軸力時固有頻率比值為：

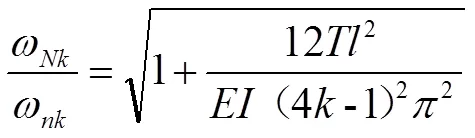
同理可得，加載軸向壓力時，前后固有頻率之比：

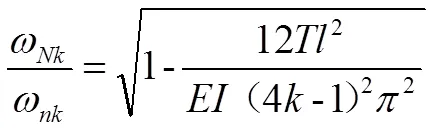
1.2 鄧克萊法近似求解多輪盤轉子的固有頻率

鄧克萊法[6]適用于忽略阻尼，且低頻遠低于高頻的情況。此法計算簡潔，多用于梁、軸振動系統。利用鄧克萊法可求出比振動系統實際基頻偏小的第一階固有頻率，可以給出基頻的下限值。

對于多輪盤轉子系統，采用柔度系數法建立振動系統的微分方程，即：

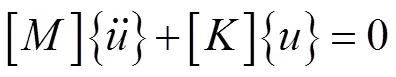
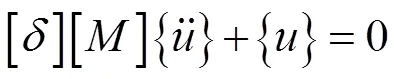
若為對角矩陣，則上式變為：

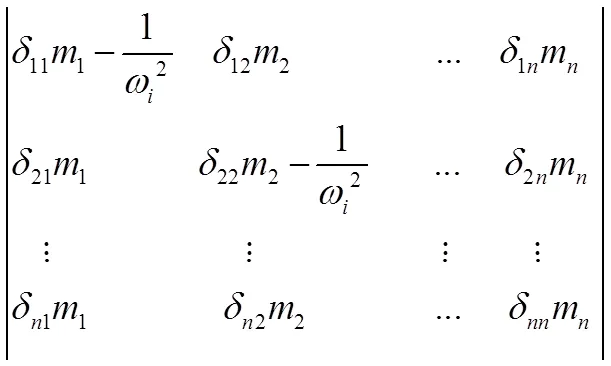
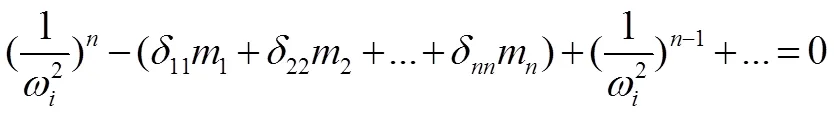
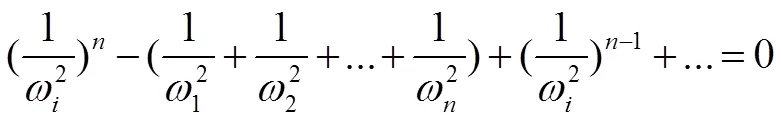
對比（1）（2）式可得：

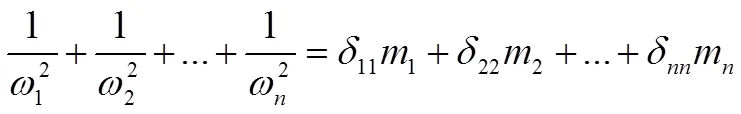
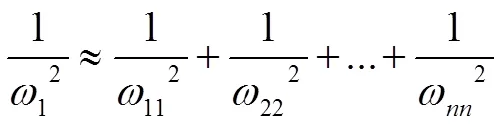
此為鄧克萊公式。

通過鄧克萊法近似計算轉子系統在剛性支承下的第一階固有頻率，根據材料力學和機械設計手冊，均勻質量軸在兩端受全約束時的一階臨界轉速為

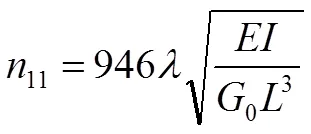
帶葉輪但不計軸自重時軸的一階臨界轉速為：

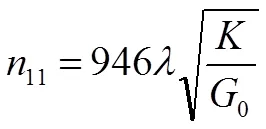
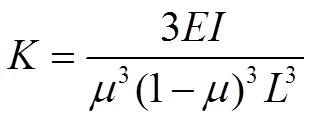
2 具有軸向力的多級離心泵轉子系統固有頻率有限元計算

應用有限元方法，對一個六級離心泵轉子部件（如圖2所示）橫向振動進行數值計算。將葉輪兩側壓力簡化為軸向力，對其進行軸向預應力的模態分析。軸總長為2 100 mm，軸的材料是45鋼，軸徑=60 mm，彈性模量=206 GPa，葉輪的材料為QT 700，彈性模量=160 GPa，密度為7 800 kg/m3，各葉輪參數見表1。

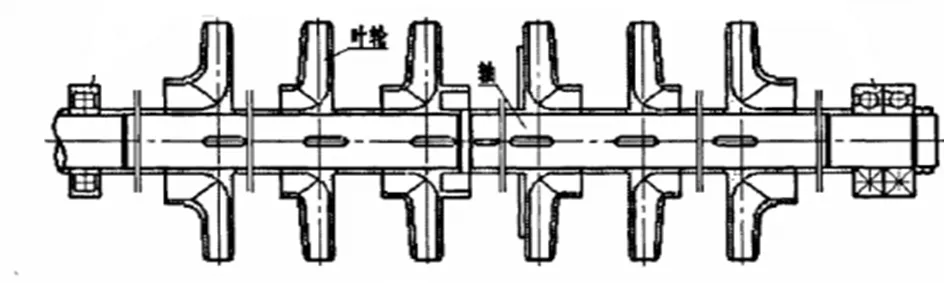
圖2 多級離心泵轉子部件示意圖

多級離心泵在工作時由于葉輪兩側壓力不等，轉軸將承受巨大的軸向力作用。若設計的軸支撐不同，葉輪兩側可承受軸向拉力或壓力。下面用有限元分析軟件，對上述六級離心泵轉子部件在分別承受軸承受軸向拉力或軸向壓力時，進行有預應力的模態分析。

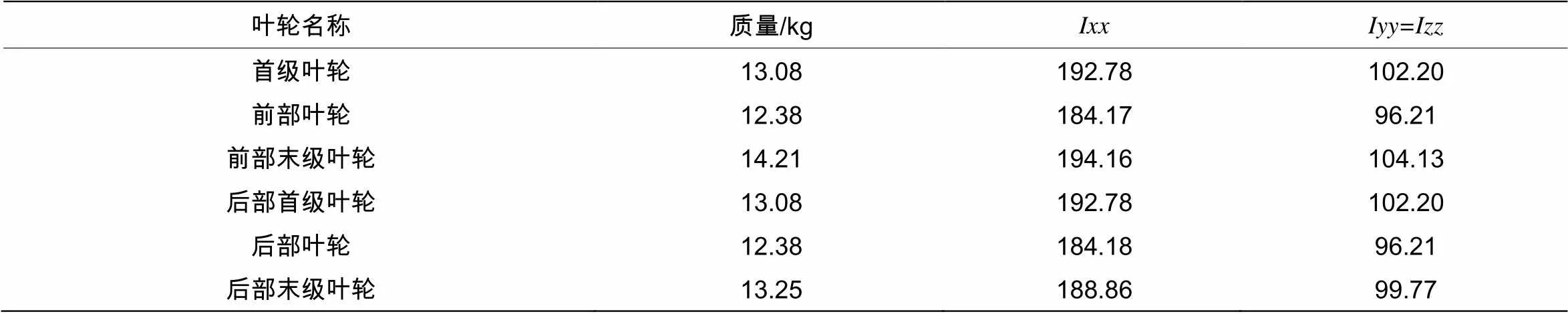
表1 離心泵葉輪參數

根據幾何模型建立有限元模型，如圖3所示。分析過程中轉軸采用剛性支承，應用梁單元+質點單元的有限元模型，其中葉輪用質量單元模擬，單元參數設置見表1中數據。軸向力加載在葉輪處質點上。

圖3 離心泵轉軸有限元模型

在每一級葉輪處承受的軸向壓力時，用有限元分析軟件做有預應力的模態分析來得到系統的固有頻率。經過數值計算得到轉軸受不同軸向壓力時的前五階彎曲振動固有頻率，具體值見表2。

表2 加載軸向壓力時轉軸系統的固有頻率

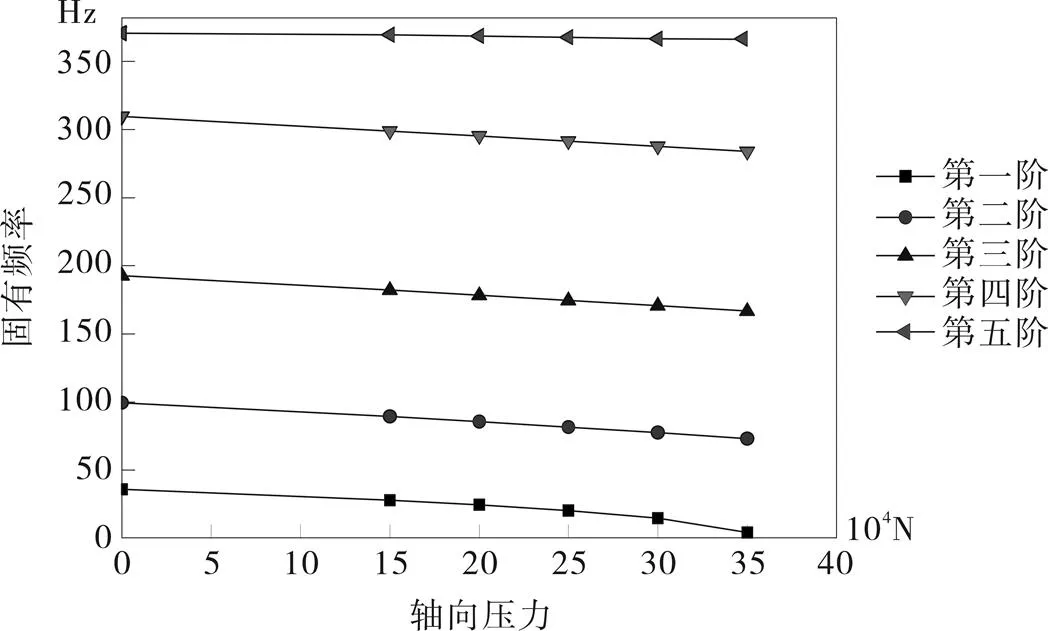
圖4 不同軸向壓力作用下轉子系統各階固有頻率變化曲線

轉軸受不同軸向拉力時的前五階彎曲振動固有頻率計算值由表3給出。

由圖4和圖5可得，當轉軸加載軸向壓力時，轉子固有頻率降低；當轉軸加載軸向拉力時，轉子固有頻率增加，軸向拉力對低階固有頻率影響較大，對高階固有頻率影響不明顯。

表3 加載軸向拉力時轉軸系統的固有頻率

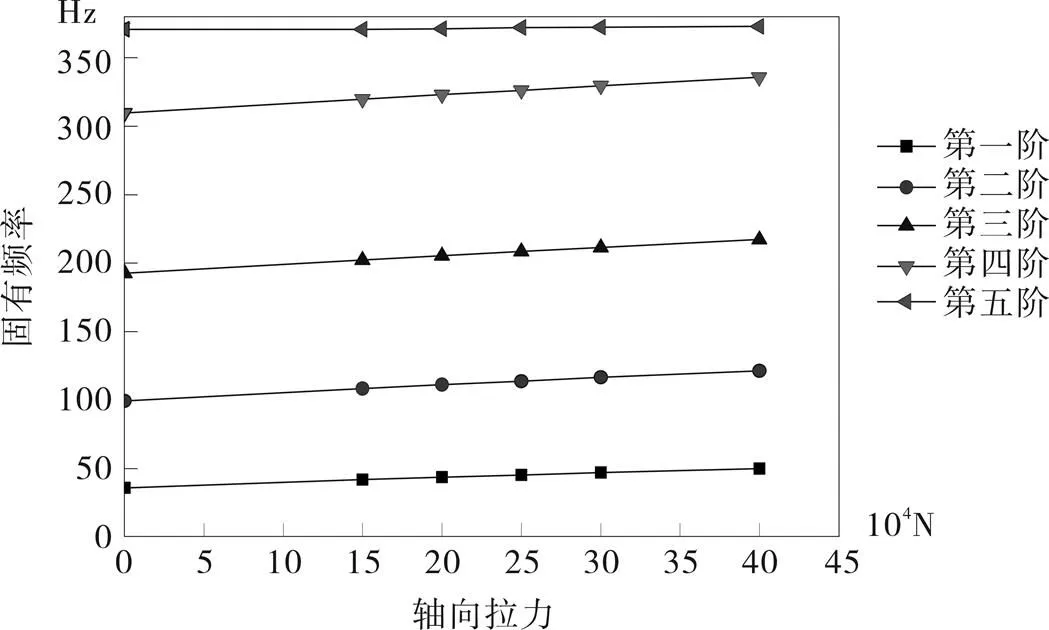
圖5 不同軸向拉力作用下轉子系統各階固有頻率變化曲線

3 結果分析及結論

根據鄧克萊公式（11）和公式（13）可計算出轉子系統一階臨界轉速為：1 993.2 r/min, 即一階固有頻率為：33.22 Hz。

表4 有限元法和鄧克萊法計算轉子的一階固有頻率

由表4可以得出，利用有限元法求出一階頻率比鄧克萊法求得的結果偏大。如前所述，鄧克萊法求解的是一階頻率的下限值，結果與應用有限元法求得結果基本符合。根據前述的理論計算和分析有：

（1）由理論解可以定性判斷軸向力對轉子系統橫向固有頻率的影響趨勢,與有限元結果保持一致，因未考慮圓盤質量，具體值與實際況存在較大誤差。利用鄧克萊法求解高速多級離心泵轉子系統的一階固有頻率，接近有限元分析結果。有限元法計算模型更接近于真實情況，求解速度快，用于求解具有軸向力轉子系統高階頻率。

（2）通過理論公式推導及應用有限元法求解轉軸系統橫向振動的固有頻率，可以得出：當轉子系統各級葉輪處加載軸向壓力時，系統固有頻率降低；當轉子系統各級葉輪處加載軸向拉力時，固有頻率增大。軸向力對轉子系統低階固有頻率影響較大，對高階固有頻率影響不顯著。為離心泵轉子部件的設計及故障診斷分析提供了一定的理論參考。

[1] 虞烈, 劉恒. 軸承一轉子系統動力學［M］. 西安: 西安交通大學出版社, 2001.

[2] 聞邦椿, 顧家柳, 夏松波, 等. 高等轉子動力學一理論、技術與應用［M］. 北京: 機械工業出版社, 2000.

[3] 孫興華, 王躍方, 郭婷. 離心泵轉子的濕態臨界轉速計算及周邊環境對其動力特性的影響[J]. 水泵技術, 2011 (2): 26-30.

[4] 張和牧, 朱漢華. 基于流固耦合的水潤滑軸承板條結構優化研究[J]. 船舶工程, 2011, 33 (4): 36-39.

Analysis on Transverse Natural Frequency of Rotating Shaft System in the High Speed Multistage Centrifugal Pump

(School of Energy and Power Engineering, Shenyang University of Chemical Technology, LiaoningShenyang 110142, China)

The rotor of the multistage centrifugal pump was simplified to the axis model of the axial force, and the lateral natural frequency was solved by using the theory method. By using the finite element method, the model of the multistage centrifugal pump shaft of the beam and particle element was established, and the modal analysis was carried out on the axis of the shaft, solving the first five orders bending vibration frequency of the shaft. The first order natural frequency of the rotor model obtained with the Dunkerley method was compared with the finite element results. Analysis results show that the axial pressure can reduce the natural frequency of the shaft, and the axial tension can increase the natural frequency of the shaft. The axial force has a great influence on the natural frequency of the rotor system, and has no significant effect on the high order frequency.

axial force; natural frequency；modal analysis；prestress

2016-11-22

岳文超（1990-），男，河北唐山人，碩士研究生在讀，主要從事轉子動力特性研究。

TQ 052

A

1004-0935（2017）01-0078-03