爆炸載荷下加筋板的動力學(xué)性能分析

崔寬++柴玉陽

摘要： 為提升軍艦、潛艇和航空母艦外板的抗爆炸載荷沖擊能力，采用Abaqus分析爆炸載荷下材料阻尼、應(yīng)變率、加筋板的幾何構(gòu)型及加強(qiáng)筋的幾何參數(shù)對結(jié)構(gòu)動力學(xué)性能的影響.結(jié)果表明：加筋板相對于平板具有優(yōu)異的抗爆炸載荷沖擊能力；材料的阻尼及應(yīng)變率對結(jié)構(gòu)動力學(xué)性能影響較大；雙十字加筋板相對于其他幾何構(gòu)型的加筋板具有更優(yōu)良的抗爆炸載荷沖擊的能力；矩形加強(qiáng)筋截面高寬比對加筋板動力學(xué)性能影響較明顯，在結(jié)構(gòu)設(shè)計(jì)中應(yīng)該根據(jù)需求進(jìn)行合理選擇.

關(guān)鍵詞： 爆炸載荷； 沖擊； 加筋板； 阻尼； 應(yīng)變率； 有限元

中圖分類號： O39；O389文獻(xiàn)標(biāo)志碼： B

Dynamics performance analysis on stiffened

plates subjected to blast loading

CUI Kuan1， CHAI Yuyang2

（1. Institute of Industry Technology， Guangzhou & Chinese Academy of Sciences， Guangzhou 511458， China；

2. School of Astronautics， Harbin Institute of Technology， Harbin 150001， China）

Abstract： To enhance the blast loading resistance ability of outer plates of warships， submarines and aircraft carriers， the effects of material damping， strain rate， geometry of stiffened plate and geometric parameters of stiffener on the dynamics performance of structure are analyzed by Abaqus. The results indicate that the stiffened plate shows better ability of resistance to blast loading than ordinary plate； the effect of material damping and strain rate on the dynamics performance of structure is great； the stiffened plate with double cross reinforcement has better ability of resistance to blast loading than other geometrical configurations； the effect of the depthwidth ratio of rectangular stiffener on the dynamics performance of stiffened plate is also obvious， and this parameter must be rationally chosen to meet the structure design requirement.

Key words： blast loading； impact； stiffened plates； damping； strain rate； finite element

收稿日期： 2016[KG*9〗11[KG*9〗15修回日期： 2016[KG*9〗11[KG*9〗29

作者簡介： 崔寬（1989—），男，河北唐山人，碩士，研究方向?yàn)榻Y(jié)構(gòu)仿真分析，（Email）cuikuan@gziit.ac.cn0引言

隨著現(xiàn)代武器多樣化發(fā)展，其殺傷性越來越強(qiáng)，對軍艦、潛艇和航母也造成巨大威脅.船舶外板力學(xué)性能的好壞直接影響其抗導(dǎo)彈打擊的能力，而外板的幾何構(gòu)造、材料及制造工藝直接影響其力學(xué)性能.設(shè)計(jì)并制造性能優(yōu)異、抗爆炸載荷能力強(qiáng)的艦船對提高中國海軍軍事實(shí)力至關(guān)重要.

在結(jié)構(gòu)設(shè)計(jì)中，為提高面板和結(jié)構(gòu)的整體承載能力，在垂直面板方向使用加強(qiáng)筋，并將加強(qiáng)筋和面板采用膠接或焊接的形式連接在一起，形成加筋板.加筋板比普通板具有更好的抗爆炸沖擊能力，目前，已有國內(nèi)外學(xué)者對其理論、仿真和試驗(yàn)進(jìn)行研究.例如，吳有生等[1]研究爆炸載荷下艦船板架的變形和破損問題；彭興寧等[2]研究爆炸載荷下艦船防護(hù)艙壁的薄膜效應(yīng)；SCHUBAK等[3]提出一種均勻分布載荷下加筋板的鋼塑性分析方法；樸春雨等[4]、侯海量等[5]和YUEN等 [6]均從仿真分析角度，對不同幾何構(gòu)型的加筋板抗爆炸沖擊性能進(jìn)行分析；JACOB等[7]、ALSOS等[8]和EHLERS[9]從試驗(yàn)方面對加筋板進(jìn)行力學(xué)性能研究.

本文利用大型通用商業(yè)有限元軟件Abaqus分析爆炸載荷下阻尼、應(yīng)變率、加筋板的幾何構(gòu)型及加強(qiáng)筋的幾何參數(shù)等對結(jié)構(gòu)動力學(xué)性能的影響.

1有限元模型建立

1.1加筋板的幾何構(gòu)型

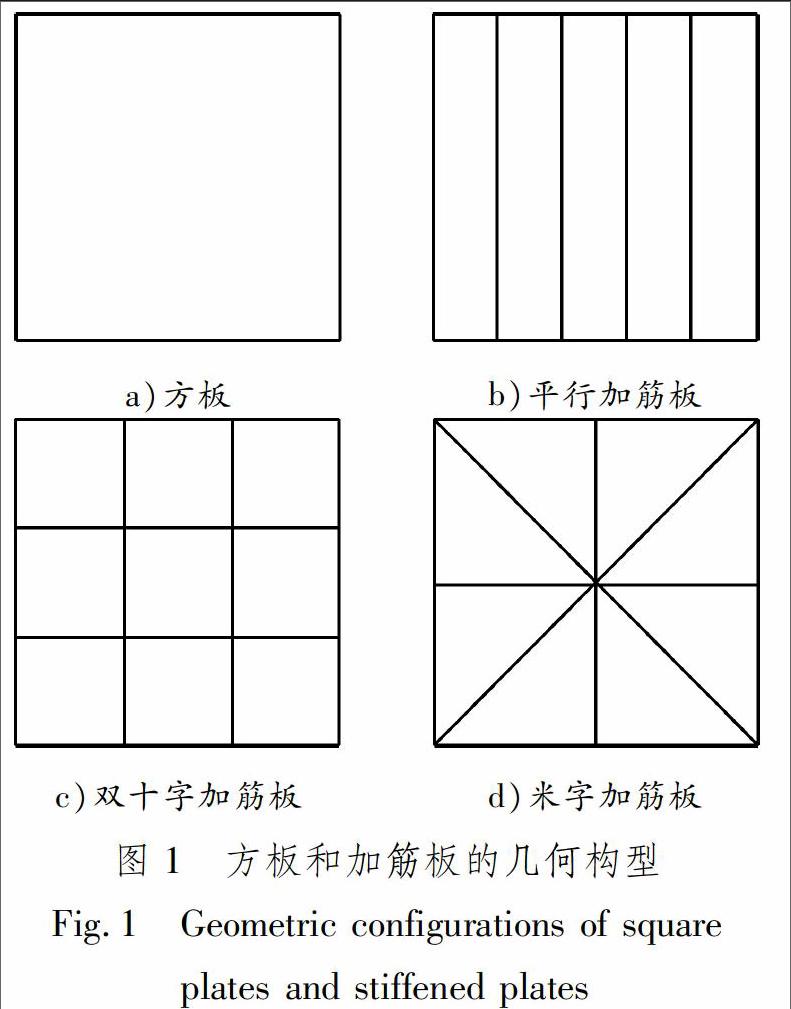
以方板模型為參照，選用方板作為加強(qiáng)筋的載體.方板的邊長為3.00 m，厚度為0.03 m.加筋板的加強(qiáng)筋數(shù)量為4根，加強(qiáng)筋的截面為矩形，筋高為0.10 m，筋寬為0.03 m.方板及加筋板的幾何構(gòu)型見圖1.

a）方板b）平行加筋板c）雙十字加筋板d）米字加筋板 圖 1方板和加筋板的幾何構(gòu)型

Fig.1Geometric configurations of square

plates and stiffened plates

1.2材料參數(shù)及單元選取

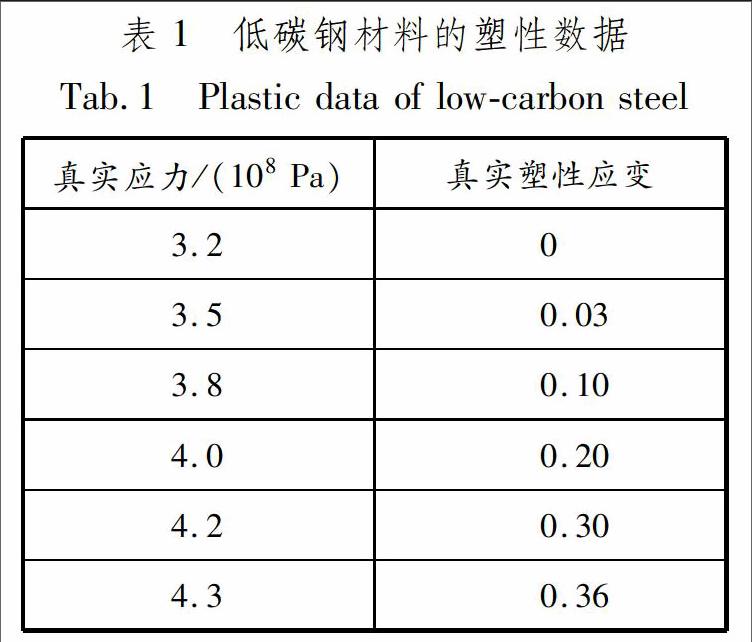
本文研究的方板和加筋板為低碳鋼材料，彈性模量為2.1×1011 Pa，泊松比為0.3，密度為7 800 kg/m3，塑性數(shù)據(jù)見表1.材料的塑性行為可以用其屈服點(diǎn)和屈服后的硬化來描述，在Abaqus中定義塑性數(shù)據(jù)必須采用真實(shí)應(yīng)力和真實(shí)應(yīng)變，塑性數(shù)據(jù)將材料的真實(shí)屈服應(yīng)力定義為真實(shí)塑性應(yīng)變的函數(shù).

表 1低碳鋼材料的塑性數(shù)據(jù)

Tab.1Plastic data of lowcarbon steel真實(shí)應(yīng)力/（108 Pa）真實(shí)塑性應(yīng)變3.203.50.033.80.104.00.204.20.304.30.36

在金屬中，塑性變形的不可壓縮性質(zhì)限制可應(yīng)用于彈塑性模擬的單元類型，這些限制來自于模擬不可壓縮材料性質(zhì)將增加對單元的運(yùn)動學(xué)約束，這種限制要求在單元積分點(diǎn)處的體積要保持常數(shù).[10]當(dāng)模擬不可壓縮性質(zhì)時，盡量不要選取完全二次積分單元.本文選用S4R單元進(jìn)行網(wǎng)格劃分.

1.3爆炸載荷

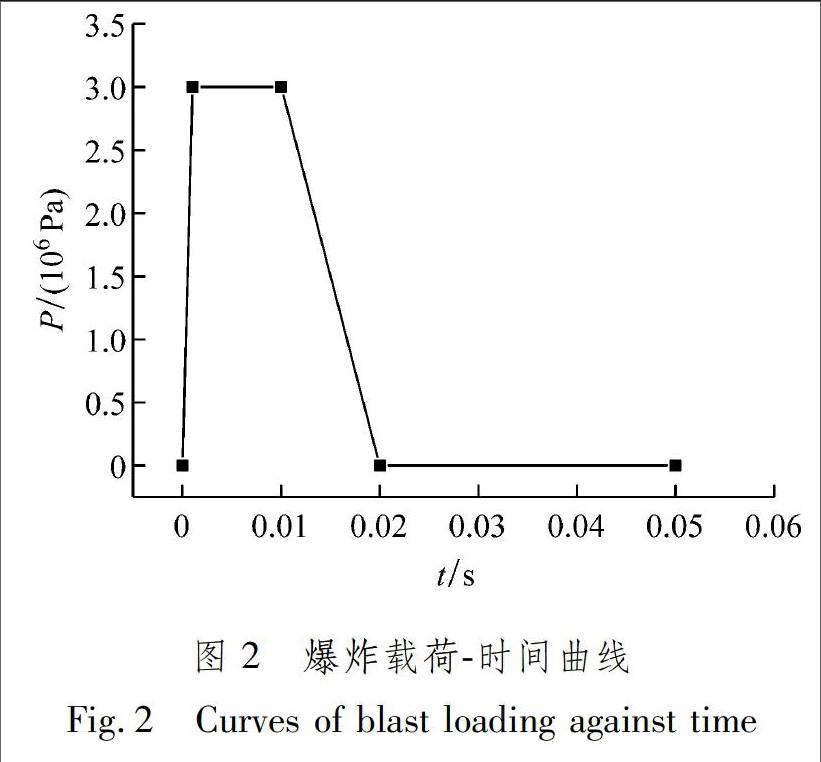
將爆炸載荷簡化為隨時間變化的壓力載荷，在分析開始時，壓力迅速增加，在0.001 s時，達(dá)到峰值3×106 N，在峰值持續(xù)0.010 s，然后在接下來的0.010 s迅速減到0，爆炸載荷隨時間變化曲線見圖2.

2阻尼及應(yīng)變率效應(yīng)

能量耗散存在于典型的結(jié)構(gòu)振動中.結(jié)構(gòu)振動的能量損失源于諸多因素，包括結(jié)構(gòu)連接處的摩擦和局部材料的遲滯效應(yīng)等.對于本文研究的方板結(jié)構(gòu)，能量損失源于支撐的摩擦阻力和空氣阻尼，通過定義Rayleigh阻尼增加結(jié)構(gòu)的阻尼效應(yīng)影響.假設(shè)阻尼矩陣C是剛度矩陣K與質(zhì)量矩陣M的線性組合，Rayleigh阻尼表達(dá)式為C=αM+βK （1）式中：α為M的比例因數(shù)；β為K的比例因數(shù).本文取α=50，β=0.

對于低碳鋼，隨著應(yīng)變速率的增加，屈服應(yīng)力也會增加，所以對應(yīng)變率相關(guān)性的研究至關(guān)重要.等效塑性應(yīng)變率ε·由動態(tài)屈服應(yīng)力與靜態(tài)屈服應(yīng)力的比值R給出，ε·=D（R-1）n（2）式中：D和n為應(yīng)變率參數(shù).本文取低碳鋼的典型值D=40，n=5.

以四邊固支的平行加筋板為研究對象，分析阻尼和應(yīng)變率參數(shù)對結(jié)構(gòu)動力學(xué)性能的影響，四邊固定約束的平行加筋板有限元模型見圖3.

2.1阻尼的影響

無阻尼結(jié)構(gòu)和有阻尼結(jié)構(gòu)的中間點(diǎn)位移響應(yīng)曲線見圖4.無阻尼加筋板的振動周期約為0.003 s，分析結(jié)果表明：質(zhì)量比例阻尼對振動衰減的影響比較大，有阻尼的結(jié)構(gòu)在0.090 s左右停止振動.

2.2應(yīng)變率的影響

無應(yīng)變率和有應(yīng)變率的結(jié)構(gòu)中心點(diǎn)位移響應(yīng)曲線見圖5.在0.008 s以后，含有應(yīng)變率的結(jié)構(gòu)位移明顯低于無應(yīng)變率的結(jié)構(gòu)，在0.010 s時兩者的位移相差最大，絕對值為0.126 m.這表明應(yīng)變率使結(jié)構(gòu)對于爆炸載荷的響應(yīng)變得剛硬.無應(yīng)變率和有應(yīng)變率的結(jié)構(gòu)的塑性耗散能見圖6.含應(yīng)變率的結(jié)構(gòu)其塑性耗散比無應(yīng)變率的結(jié)構(gòu)的塑性耗散能減少36%左右.

3加筋板幾何構(gòu)型的影響

方板和3種幾何構(gòu)型的加筋板位移云圖見圖7，3種不同幾何構(gòu)型加筋板和方板的中心點(diǎn)位移響應(yīng)曲線見圖8.由圖7和8可知：加筋板相對于平板具有很好的抵抗爆炸載荷的能力；方板在爆炸載荷的激勵下，位移最大為0.226 m；最終4種結(jié)構(gòu)在阻尼的作用下逐漸達(dá)到平衡狀態(tài)；雙十字加筋板相對于另2種幾何構(gòu)型的加筋板位移最小，說明雙十字加筋板具有更好的抵抗變形的能力.

4加強(qiáng)筋幾何參數(shù)的影響

不同截面尺寸的加強(qiáng)筋具有不同的抗彎剛度，研究矩形截面加強(qiáng)筋的截面參數(shù)對結(jié)構(gòu)在爆炸載荷作用下的響應(yīng).以平行加筋板為研究對象，在不改變加強(qiáng)筋截面尺寸的情況下，分析截面高度和寬度的影響，加強(qiáng)筋的不同截面尺寸和高寬比見表2.不同加強(qiáng)筋截面的結(jié)構(gòu)的中心點(diǎn)位移響應(yīng)曲線見圖9.由圖9可知：隨著加強(qiáng)筋截面高寬比的增加，加筋板中心點(diǎn)的位移響應(yīng)呈減小趨勢，結(jié)構(gòu)A相對于結(jié)構(gòu)D的中心點(diǎn)位移減少8.6%.分析結(jié)果表明，隨著矩形截面高寬比的增加，加筋板抵抗爆炸載荷的能力增強(qiáng).

a）方板的位移云圖

b）平行加筋板的位移云圖

c）雙十字加筋板的位移云圖

d）米字加筋板的位移云圖

three stiffened plates圖 8方板和加筋板的中心點(diǎn)位移響應(yīng)

Fig.8Center point displacement responses of

square plates and stiffened plates

5結(jié)束語

從材料阻尼、應(yīng)變率、幾何構(gòu)型及加強(qiáng)筋截面幾何參數(shù)等4個方面，對結(jié)構(gòu)的抗爆炸載荷沖擊的能力進(jìn)行分析.阻尼和應(yīng)變率效應(yīng)對加筋板在爆炸載荷作用下的響應(yīng)影響較大，阻尼最終使結(jié)構(gòu)趨于平衡穩(wěn)定狀態(tài)，應(yīng)變率使結(jié)構(gòu)具有更強(qiáng)的抵抗爆炸載荷沖擊的作用.加筋板具有良好的抵抗爆炸載荷的能力，雙十字加筋板相對于另2種幾何構(gòu)型的加筋板抵抗爆炸載荷的能力更強(qiáng).對于矩形截面加強(qiáng)筋，其截面高寬比對于加筋板在爆炸載荷下的性能影響較大，在允許的情況下，增大高寬比可以提升結(jié)構(gòu)的抗爆炸載荷沖擊的能力.

參考文獻(xiàn)：

[1]吳有生， 彭興寧， 趙本立. 爆炸載荷作用下艦船板架的變形與破損[J]. 中國造船， 1995， 36（4）： 5561.

WU Y S， PENG X N， ZHAO B L. Plastic deformation and damage of naval panels subjected to explosion loading[J]. Ship Building of China， 1995， 36（4）： 5561.

[2]彭興寧， 聶武， 嚴(yán)波， 爆炸載荷作用下艦船防護(hù)艙壁的薄膜效應(yīng)研究[J]. 船舶力學(xué)， 2007， 11（5）： 744751.

PENG X N， NIE W， YAN B， Analysis of membrane effect of surface warships protective bulkhead subjected to blast loading[J]. Journal of Ship Mechanics， 2007， 11（5）： 744751.

[3]SCHUBAK R B， OLSON M D， ANDERSON D L. Rigidplastic modeling of blastloaded stiffened platesPart I： oneway stiffened plates[J]. International Journal of Mechanical Sciences， 1993， 35（3/4）： 289306.

[4]樸春雨， 章怡寧. 典型加筋板的優(yōu)化設(shè)計(jì)[J]. 飛機(jī)設(shè)計(jì)， 2003（4）： 2933.

PIAO C Y， ZHANG Y N. Optimal design of typical stiffened panels[J]. Aircraft Design， 2003（4）： 2933.

[5]侯海量， 朱錫， 谷美邦. 爆炸載荷作用下加筋板的失效模式分析及結(jié)構(gòu)優(yōu)化設(shè)計(jì)[J]. 爆炸與沖擊， 2007， 27（1）： 2633.

HOU H L， ZHU X， GU M B. Study on failure mode of stiffened plate and optimized design of structure subjected to blast load[J]. Explosion and Shock Waves， 2007， 27（1）： 2633.

[6]YUEN S C K， NURICK G N. Experimental and numerical studies on the response of quadrangular stiffened plates. Part I： subjected to uniform blast load[J]. International Journal of Impact Engineering， 2005， 31（1）： 5583. DOI： 10.1016/j.ijimpeng.2003.09.048.

[7]JACOB N， YUEN S C K， NURICK G N， et al. Scaling aspects of quadrangular plates subjected to localised blast loads： experiments and predictions[J]. International Journal of Impact Engineering， 2004， 30（8/9）： 11791208. DOI： 10.1016/j.ijimpeng.2004.03.012.

[8]ALSOS H S， AMDAHL J. On the resistance to penetration of stiffened plates， Part I： Experiments[J]. International Journal of Impact Engineering， 2009， 36（6）： 799807. DOI： 10.1016/j.ijimpeng.2008.10.005.

[9]EHLERS S. Strain and stress relation until fracture for finite element simulations of a thin circular plate[J]. ThinWalled Structures， 2010， 48（1）： 18. DOI： 10.1016/j.tws.2009.08.004.

[10]莊茁， 張帆， 岑松， 等. Abaqus非線性有限元分析與實(shí)例[M]. 北京： 科學(xué)出版社， 2005： 239244.（編輯武曉英）第26卷 第1期2017年2月計(jì) 算 機(jī) 輔 助 工 程Computer Aided EngineeringVol.26 No.1Feb. 2017