基于跳距修正L-M優化的WSN定位算法

喬 欣，史良馬，楊漢生，丁恩杰，王正創

(1.巢湖學院 機械與電子工程學院，安徽 巢湖 238000；2.中國礦業大學 物聯網(感知礦山)研究中心，江蘇 徐州 221008)

基于跳距修正L-M優化的WSN定位算法

喬 欣1，史良馬1，楊漢生1，丁恩杰2，王正創1

(1.巢湖學院 機械與電子工程學院，安徽 巢湖 238000；2.中國礦業大學 物聯網(感知礦山)研究中心，江蘇 徐州 221008)

針對DV-Hop定位算法在節點隨機分布的網絡拓撲環境下存在誤差較大的問題，文中通過分析平均跳距估計、未知節點坐標估計區域求解對定位精度的影響，提出了一種基于跳距修正L-M優化的WSN定位算法CLDV-Hop(Correct L-M DV-Hop)；仿真結果表明，在不增加額外開銷且仿真環境相同的條件下，CLDV-Hop算法比現有改進的算法具有更高的定位精度，與DV-Hop算法相比精度提高了約33%～41%。

WSN；跳距修正；L-M優化

0 引言

無線傳感器網絡(wireless sensor network，WSN)是由布撒在區域內能夠感知、處理、傳輸環境信息的大量傳感器節點組成，通常被用于環境監測、醫療服務、軍事偵查、工業診斷、智能空間等領域[1]。不管是何領域，缺少目標或傳感器節點位置信息的研究都是無意義的。因此，節點定位技術成為WSN中的重要研究課題。

目前，較為成熟的GPS定位系統可以實現WSN的節點定位，但考慮到價格、體積、能耗及環境等因素，故不可能大規模地布置[2]。許多研究者針對無需GPS模塊提出了各種定位算法，根據定位機制可劃分為基于測距的定位算法(Range-Based)和與距離無關的定位算法(Range-Free)[3]。前者需要測量相鄰節點間的絕對距離或者角度信息，常用的測距技術有RSSI、TOA、TDOA、AOA。后者僅根據網絡的連通性等信息即可實現定位[4]。如質心算法、凸規劃算法、APIT算法及DV-Hop算法等[5]。Range-Based對硬件要求較高，并且需要多次測量來獲得合理的定位精度，所以計算量和通信開銷很大。Range-Free定位機制憑借其在成本、功耗、復雜度等方面的優勢，被廣泛應用在大WSN。

DV-Hop是一種典型的無需測距定位算法，實現簡單、定位精度較高[5]。但是，在節點隨機分布的WSN中，該算法的定位精度仍然不足[6]，故針對該算法精度、穩定性、效率等存在的問題，很多學者提出了相應的改進方案。文獻[7]提出利用三角不等式對未知節點到多跳錨節點的距離進行約束，同時采用加權雙曲線進行定位；文獻[8]提出用全新的方法計算錨節點到未知節點的距離、利用加權最小二乘法進行定位計算。本文提出了CLDV-Hop算法，并且與文獻[7]、文獻[8]中所述算法進行仿真分析，結果表明，在節點隨機分布的網絡拓撲結構中，CLDV-Hop算法具有更高的定位精度與穩定性。

1 算法描述與誤差分析

1.1 DV-Hop算法

DV-Hop算法的定位過程如下：

Step1 錨節點廣播自身信息并計算平均跳距[9]。錨節點將自身信息以數據包的格式廣播至網絡的所有節點。由圖1網絡結構拓撲可知，錨節點i,j之間的跳數為hij=3，未知節點p與錨節點i的跳數為hip=3。

已知錨節點的坐標(x,y)與錨節點間的跳數h，那么可以根據公式(1)計算出每個錨節點的平均跳距HS。

(1)

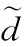
Step3 定位階段。如果網絡中未知節點能夠收到三個或者三個以上錨節點的信息，則可以執行三邊定位法或最大似然估計法求解未知節點的坐標。

假設待求未知節點p坐標為(x,y)，第i個錨節點的坐標記為(xi,yi)，節點p到錨節點i的距離記為di。若WSN中有m個錨節點能夠與未知節點p通信，則未知節點p的坐標可以根據式(2)方程組估計得出。

(2)

上述方程組可以轉化為AX=b的形式。

方程AX=b利用最小二乘法解未知節點的估計坐標為：

X=(ATA)-1ATb

(3)

圖1 網絡拓撲結構

2 CLDV-Hop算法

本節中，在不增加網絡通信量、硬件開銷，不改變DV-Hop算法過程的條件下，本文對平均跳距和定位估計兩個方面進行了改進。

2.1 平均跳距修正

DV-Hop算法中獲得較為合理的平均跳距是保證定位精度的關鍵，本節，從兩個方面對平均跳距進行修正，具體步驟如下：

1)節點在定位過程中，網絡節點隨機分布，當通信半徑r一定時，在節點分布的局部區域可能會形成“空洞”，使得距離一定的錨節點之間的跳數值可能變大，這就導致求解平均跳距誤差變大[10]。本文首先設定錨節點的跳數閾值δ，當hij>δ時，令hij=0，dij=0。

2)在估計未知節點的坐標時，未知節點將最先接收到錨節點平均跳距的信息作為其平均跳距。就整個節點非均勻分布的網絡而言，不足以表示整個網絡的平均跳距，可能會引起局部的定位精度偏差很大，使得整個網絡的定位精度不穩定。因此，綜合考慮多個錨節點的平均跳距，能夠提高整個網絡的定位精度。

假設有m個錨節點，結合公式(1)，錨節點j平均跳距的修正因子?j可表示為：

(4)

2.2 基于L-M法優化的定位估計

在DV-Hop算法中，如果能夠確定3個或者3個以上錨節點到未知節點的距離，則可以通過三邊或者多邊定位法對未知節點的坐標進行估計[11]。事實上，盡管通過平均跳距的修正，未知節點到錨節點的跳段距離的估計也總是存在誤差，因為多邊定位法對測距誤差敏感，當測距誤差較大時，通過多邊定位法計算出的估計坐標與真實坐標之間存在更大的偏差，另外，在仿真過程中發現，當ATA為病態矩陣時，通過多邊定位法所估計出的未知節點坐標不僅誤差很大，而且定位精度的穩定性較差，有時甚至得出錯誤的結果[9]。

本文采用多邊定位法和L-M算法相結合的算法求解未知節點的估計坐標，即首先通過多邊定位法獲得未知節點的估計坐標，然后把估計值作為L-M算法的初值，進一步對未知節點坐標迭代求精。圖2畫出了錨節點為10時，其中一個未知節點的估計區域。

圖2 未知節點估計區域

從式(2)中可以看出，該方程組為超定方程組。因此，將式(2)轉換成：

(5)

式中，X為未知節點坐標(x,y)，r(X)為殘差函數。

由此可將求解未知節點的估計坐標轉化為求式(5)的無約束極小平方和問題，即minF(X)。L-M法在處理非線性最小二乘優化問題上具有明顯的優勢，本文中選用L-M法進行優化。

L-M算法的迭代公式可以表示為：

(6)

其中：X(0)為通過式(4)求得未知節點的最小二乘解求的坐標初值(x,y)，k為迭代變量，μ為阻尼參數，μ>0。r(X(k))為：

r(X(k))=(r1(X(k)),(r2(X(k)),…,(rm(X(k)))

J(X(k))為殘差函數r(X)在X(k)處一階導數組成的雅克比矩陣：

(7)

2.3CLDV-Hop定位算法的過程

CLDV-Hop算法步驟如下：

Step1:網絡初始化。同時給出文中仿真相關變量，如下表所示。

表1 仿真變量及參數設置

Step2:錨節點通過洪泛廣播的方式發送信息，包括自身ID、坐標、跳數。

Step3:最短路徑算法計算節點間跳數、根據式(1)計算每個錨節點的平均跳距Dhop(AnchorAmount,1)并廣播至網絡、未知節點從最近的3個錨節點獲得加權平均跳距UNWDhop(UNAmount,1)，通過跳數與平均跳距的乘積估算出未知節點到錨節點的距離DAll(AnchorAmount,UNAmount)。

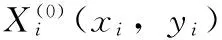
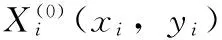
Step6:通過平均定位誤差、歸一化平均定位誤差、均方根誤差對CLDV-Hop算法進行評價。

3 仿真與實驗

為了驗證改進后算法的性能，本文利用MATLAB 2010b平臺對文中提出的CLDV-Hop定位算法進行仿真分析，并同有關方法進行了比較。仿真環境區域大小為100 m×100 m，并在該區域內隨機放置100個節點，圖3為網絡節點隨機分布圖。其他仿真參數參考表1。

圖3 網絡節點隨機分布圖

圖4仿真了錨節點數20、通信半徑30時， DV-Hop和CLDV-Hop對未知節點定位的偏差。從圖中可以看出，改進后算法的定位精度明顯比DV-Hop算法精度高的多。

圖4 未知節點定位偏差圖

圖5、6中分別對比了文獻[7]通過加權雙曲線定位算法(記為WDV-Hop)、文獻[8]采用新的方式計算未知節點與錨節點距離的算法(記為NDV-Hop)及傳統DV-Hop算法，仿真了幾種算法歸一化平均定位誤差與網絡節點總數的關系。圖5中設置通信半徑為20，錨節點為15個，從圖中可以看出，隨著網絡節點總數的增加，文中提出的CLDV-Hop算法歸一化平均定位誤差更低。圖6中設置通信半徑為30，錨節點數為15個，從圖中可以看出，節點總數為150個時，DV-Hop算法歸一化誤差為0.321 4，NDV-Hop算法約為0.240 8，WDV-Hop算法約為0.231 7，而文中提出的CLDV-Hop算法僅為0.198 7。從圖5、6對比可以看出，通信半徑取值不同對定位精度影響較大，每個無線傳感網絡中都存在一個最優通信半徑的問題，實際應用中要多次測試選擇最優的通信半徑。

圖5 通信半徑為20時，網絡節點總數對定位誤差的影響

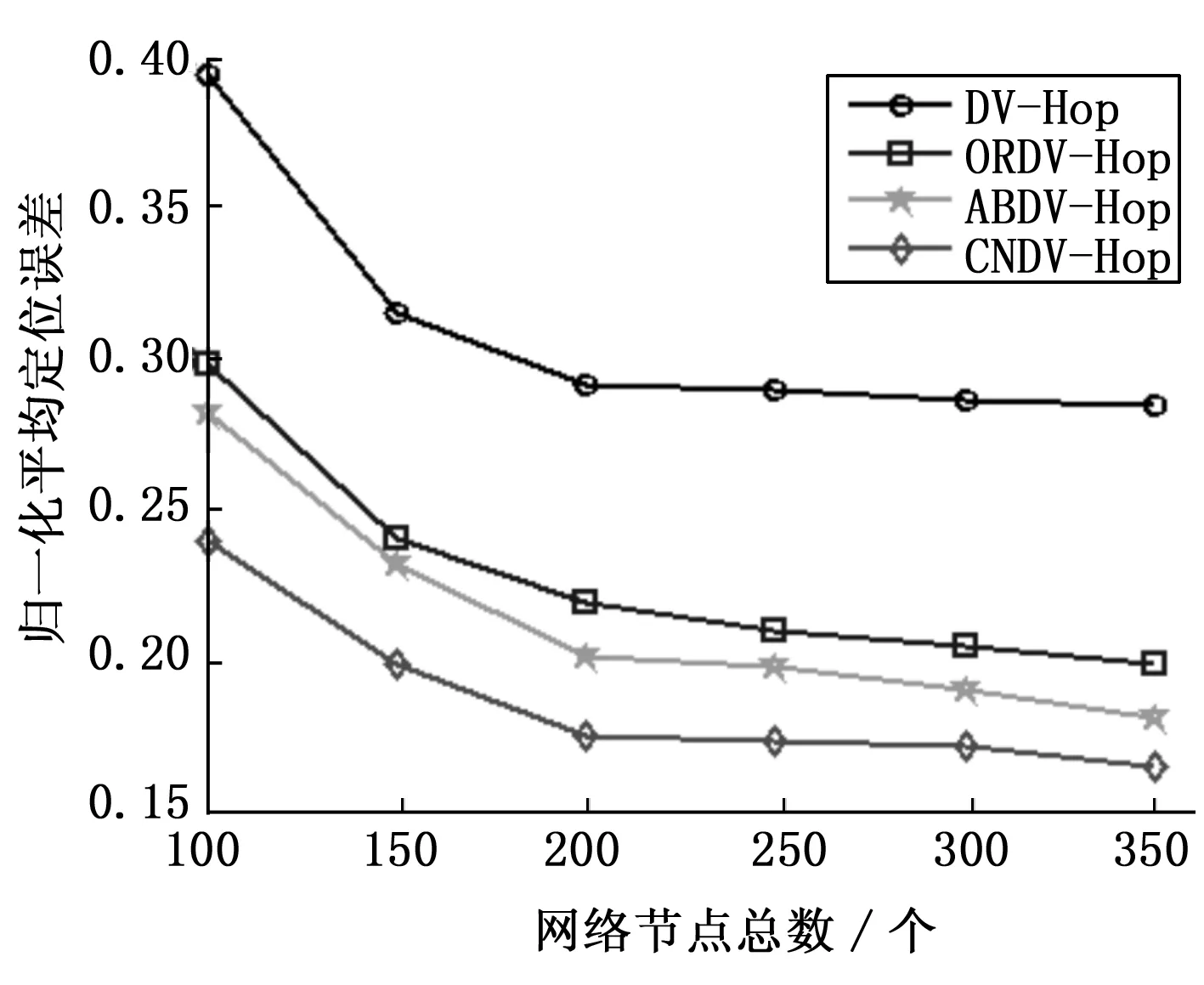
圖6 通信半徑為30時，網絡節點總數對定位誤差的影響

4 結論

本文提出了一種基于跳距修正L-M優化的WSN定位算法，能夠應用在節點隨機分布的大型無線傳感器網絡定位監測，如地質災害監測、水質污染監測、森林火災監測等。文中通過對平均跳距、定位計算兩個方面分別進行改正，通過仿真

實驗可以得出本文算法定位精度更高，是一種簡單高效的WSN非測距定位算法。

[1]賈 琦，周新志.基于無線傳感器網絡DV-HOP定位算法的改進和研究[J].計算機測量與控制,2013,21(11)：3043-3046.

[2] Capkun S, Hamdi M, Hubaux J P. GPS-free positioning in mobile Ad-Hoc networks[A]. Proc. Hawaii Int. Conf. on System Sciences[C]. Maui, HW, USA, 2001：3481-3490.

[3] 石為人,賈傳江,梁煥煥.一種改進的無線傳感器網絡DV-Hop定位算法[J].傳感技術學報,2011,24(1):83-87.

[4] Girod L, Bychkovskiy V, Elson J. Locating tiny sensors in time and space: A case study[A]. Proceedings of the 2002 IEEE International Conference on Computer Design[C]. Freiburg (Germany) , 2002: 214-219.

[5] Niculescu D,Nath B. DV Based Positioning in Ad Hoc Networks[J].Journal of Telecommunication Systems, 2003, 22(1-4):267-280.

[6] He T, Huang C D, Blum B M, et al. Range-Free Localization Schemes for Large Scale Sensor Networks[A]. Proceedings of the Ninth Annual International Conference on Mobile Computing and Networking[C]. San Diego, United states，2003:81-95.

[7] 周 玲,康志偉,何怡剛.基于三角不等式的加權雙曲線定位DV-HOP算法[J].電子測量與儀器學報,2013,27(5)：389-395.

[8] 朱 敏，劉昊霖，張志宏,等.一種基于DV-HOP改進的無線傳感器網絡定位算法[J].四川大學學報(工程科學版)，2012，44(1)：93-98.

[9] 喬 欣，常 飛，丁恩杰,等.基于跳距修正的WSN擬牛頓迭代定位算法[J].傳感技術學報，2014,27(6)：797-801.

[10]Ding E J, Qiao X, Chang F. Iterative algorithm for Quasi-Newton in WSN based on modifying average hopping distances[J]. WIT Transactions on Engineering Sciences, 2014(87):589-596.

[11] Ding E J, Qiao X, Chang F. Improved weighted Centroid localization algorithm based on RSSI differential correction[J]. International Journal on Smart Sensing and Intelligent Systems, 2014,7(3):1156-1173.

Iterative Algorithm for L-M in WSN Based on Modifying Average Hopping Distances

Qiao Xin1, Shi Liangma1, Yang Hansheng1, Ding Enjie2，Wang Zhengchuang1

(1.School of Mechanical and Electrical Engineering, Chaohu University, Chaohu 238000, China；2.CUMT-IoT Perception Mine Research Center，Xuzhou 221008，China)

Aiming at the existing large errors of the DV—Hop localization algorithm in network topology nodes distributed randomly, the passage try to solve the position accuracy by analyzing the estimate of the average hop and the unknown node coordinates region, proposed a CLDV-Hop algorithm in WSN based on modifying average hopping distances. The simulation results show that, without increasing the overhead and the same conditions as the simulation environment, CLDV-Hop algorithm has higher positioning accuracy than existing improved algorithms, and compared with DV-Hop algorithm accuracy is improved by about 33%～41%.

WSN; average hop distance correction; L-M optimization

2016-07-15；

2016-09-22。

安徽省高校省級科學研究重點項目(KJ2012A203);巢湖學院校級項目(XLY-201603)。

喬 欣(1988-)，女，安徽宿州人，碩士，助教，主要從事無線傳感器網絡定位技術，ZigBee技術等方向的研究。

1671-4598(2017)02-0116-04

10.16526/j.cnki.11-4762/tp.2017.02.032

TP393

A