基于混合范數的來波方位估計
謝前朋,王倫文
(解放軍電子工程學院,安徽 合肥 230037)
基于混合范數的來波方位估計
謝前朋,王倫文
(解放軍電子工程學院,安徽 合肥 230037)
針對傳統MUSIC算法以及CS-MUSIC算法在相干和非相干信源的條件下DOA估計效果不理想問題,提出基于混合范數的來波方位估計方法。該方法利用MUSIC和壓縮感知稀疏恢復的特性得到信號的支持域,然后由信號的支持域得到噪聲子空間和信號子空間,把得到的信號子空間和噪聲子空間與經典MUSIC算法相結合,得到高分辨率的來波方位估計方法。仿真結果表明,在非相干信源的條件下,該算法性能優于MUSIC和CS-MUSIC算法;同時,該算法相關信源的角度分辨率也優于CS-MUSIC算法。
DOA估計;CS-MUSIC;壓縮感知;混合范數
0 引言
窄帶遠場信號的來波方位估計在無線通信、雷達聲吶系統、聲源定位、醫學成像和地震學中得到了廣泛的應用。經典子空間估計算法如MUSIC算法在理想的條件下能得到高分辨率的來波方位估計,但是,在信噪比比較低和快拍數比較小的情況下,其會產生子空間泄露問題[1],即一些信號子空間泄露到噪聲子空間之中從而導致算法性能的下降。同時,MUSIC算法同樣也不能處理相關信源的DOA估計問題。
由于信號在空間域的稀疏性,空間信源數遠遠小于所有可能劃分的空間角度數,使壓縮感知在DOA估計中得到了廣泛的應用。壓縮感知能降低采樣速率以及傳感器陣列的數目,同時在工程上能降低軟件與硬件的復雜度。
壓縮感知中的稀疏恢復算法能在未知的稀疏矢量空間中找到非零元素的位置,這在DOA估計中非常重要,常用的稀疏恢復算法是凸優化算法[2-3]和貪婪算法[4-5]。貪婪算法能夠降低計算的復雜度,凸優化算法一般是基于l0,l1,l2范數。在這三種范數中,l2范數存在非稀疏解[6],使用l0范數能夠得到精確的解但是會導致NP-hard問題[7]。因此,在特定的條件下,l1范數被用來對稀疏信號進行精確恢復,使其和l0范數有相同的解[8]。三種算法均能夠處理單快拍和多快拍數條件下的DOA估計,分為單觀測矩陣矢量算法和多觀測矢量矩陣算法。但是,三種算法在單獨使用時都會出現不足。本文針對上述問題,提出了基于混合范數的來波方位估計方法。
1 信號模型
1.1 基于MUSIC算法的信號模型
假設N個窄帶遠場信號源si(t)入射到M元均勻線陣上,接收信號模型可以表示為如下:
X=AS+W
(1)
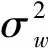
以MUSIC算法為代表的傳統DOA估計算法基于奇異值分解,利用噪聲子空間和信號子空間的正交性來實現高分辨率的DOA估計。接收信號的協方差矩陣為:
RXX=E{XXT}
(2)
對RXX進行奇異值分解,得到信號子空間QS∈CM×N和噪聲子空間QW∈CM×(M-N),從而得到MUSIC算法的空間譜估計如下:
(3)
由于信號子空間與噪聲子空間的正交性,利用MUSIC算法進行測向時,得到的最大的峰值方向就是信號的來波方向。在高信噪比的條件下,MUSIC算法能得到較好的性能,但是其有兩方面的不足[9]:需要知道信源的個數以及只能對非相干信源進行DOA估計。
1.2CS-MUSIC
把空間角度劃分為G份,[θ1,θ2,…,θG],G?N,在稀疏域的DOA估計模型如下:
X=ΨS+W
(4)
式(4)中,S=[s1(t),…,sG(t)]T中有N個非零的列,Ψ∈CM×G是過完備原子基。利用l1范數對上式進行求解,找出S中最大的N個元素值:
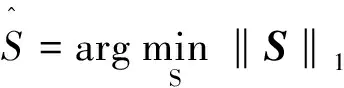
(5)
在快拍數為單快拍的條件下,對應的模型是單測量矢量模型(Single Measurement Vectors,SMV),否則是多測量矢量模型(Multiple Measurement Vectors, MMV)問題。對于單快拍SMV問題,除了凸優化的解決方法,貪婪算法通過迭代運算也能得到稀疏系數的解。對于SMV問題的求解最常用的兩種貪婪算法是正交匹配追蹤和基追蹤算法。對于MMV問題,算法應該能恢復出聯合稀疏矩陣S。一般使用混合范數來求解聯合稀疏矩陣S:
(6)
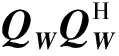
(7)
式(7)中,j?{1,…,G}表示Ψ的列。在相干信源的情況下,rank(S)=r (8) 圖1的流程圖說明了本文所提算法的步驟,壓縮感知是以概率性的方式重構空間譜,而MUSIC算法是以確定性的方式構造空間譜。壓縮感知突出的優勢是在較少的快拍數的情況下具有較高的分辨率,其特殊的重構方式使得該方法具有抗干擾性,但隨著快拍數的增加,壓縮感知算法不能給出尖銳的譜峰,而MUSIC算法在快拍數較多時能得到尖銳的譜峰。因此使用混合l1,2范數與MUSIC算法相結合能實現比其他MMV稀疏恢復算法或傳統DOA估計算法更好地測向性能。 利用本文算法來進行來波方位估計包含以下三個步驟:1)由于本文算法在處理DOA估計時,需要知道信號源的數目,因此,在信源數目未知時首先利用蓋氏圓方法(Gerschgorin)[11]對信號源數目進行估計,蓋氏圓方法在相關信源,白噪聲和色噪聲的條件下均能精確的估計出信源數; 2)在得到信號源數目的條件下,利用l1,2范數最小化求出SuppS(N-r);3)找出SuppS中剩余的r個元素,然后使用MUSIC算法進行DOA估計。為了降低式(4)中X的維數,首先進行奇異值分解: X=UDrVT (9) 式(9)中,Dr∈Cr×r是包含最大奇異值的滿秩對角矩陣,U∈CM×r和V∈CK×r分別是對應的酉矩陣。降維后的信號模型為: XSV=ΨSSV (10) 式(10)中,XSV=XV,SSV=SV。把降維后的式(10)首先利用l1,2范數最小化求出SuppS(N-r)的下標: (11) 式(11)中,σ2表示稀疏恢復需要的噪聲門限,把通過上式求出的SuppS記為IN-r。然后通過MUSIC算法找出SuppS中剩余的r個下標。從Ψ中選擇下標為IN-r的元素記為ΨIN-r從而形成新的噪聲子空間。對于其他下標的元素利用式(8)找到非零元素的下標并且按升序排列。 本文提出一種新的混合l1,2-MUSIC算法,盡管l2,1-MUSIC算法在文獻[12]中被提出,但是本文算法從另一個角度來對來波方位進行估計。所提算法把壓縮感知以概率性的方式重構空間譜和MUSIC算法以確定性的方式構造空間譜結合起來。并且使用新的兩種范數對信號進行恢復同時不需要考慮信源的相關就能得到完整的信號支持域SuppS,克服了傳統MUSIC算法以及CS-MUSIC算法的不足。通過在劃分的空間網格上重新排列SuppS的下標,利用壓縮感知稀疏恢復算法能得到精確的高分辨率信號的來波方位。 由于在實際的來波方位估計中,正弦信號、高斯信號和線性調頻信號得到了廣泛的應用,本文把這三種信號應用于所提出的算法中,通過本文算法在三種不同信號中的應用來說明所提算法能夠應用于實際的信號來波方位估計中。 為了說明本文算法的有效性,通過與MUSIC算法以及CS-MUSIC算法進行對比。算法的性能通過不同信噪比下的均方誤差、不同快拍數下的均方誤差以及對相關信源的分辨能力來進行說明。分別在信源為正弦信號、高斯信號以及線性調頻信號的情況下比較三種算法的性能。同時定義克拉美羅界如下[13]: (12) 式(12)中,K表示快拍數,M表示陣元的數目,d表示陣元間距,θ表示方位角。 3.1 不同信噪比下的均方誤差實驗 正弦信號的頻率設置為100 Hz,高斯信號的方差設置為σ=0.01,線性調頻信號的頻率隨時間線性變化,初始值設置為100 Hz,以0.1 Hz的速率進行增加。所有的結果是100次獨立蒙特卡羅實驗的平均,圖3表示三種算法的均方誤差隨信噪比的變化。陣元數為10,陣元間距為λ/2,采用50個快拍的接收數據。信噪比的變化范圍為[-5,20]dB。入射信號來自于40°方向,把[0,180°]的角度劃分間隔為1 801份。對于MMV問題下的SuppS,本文算法通過混合l1,2范數最小化和MUSIC算法來求解,而CS-MUSIC通過SOMP和MUSIC來求解。 從圖2中可以看出:當信號為正弦信號時本文算法的性能優于MUSIC算法以及CS-MUSIC算法;但對于高斯信號以及線性調頻信號在信噪比較低時,本文算法性能差于其他兩種算法。這是因為高斯信號以及線性調頻信號在頻率域不具有稀疏性。 3.2 不同快拍數下的均方誤差實驗 快拍數的變化范圍為[1,1 000],陣元數為12,SNR=0 dB,信源來波方位為40°,其他實驗條件不變。從圖3中可以看出在低快拍數的條件下,本文所提算法優于MUSIC算法和CS-MUSIC算法。 3.3 三種算法對相關信源的分辨率實驗 兩個相關正弦信號來自于不同的方向,陣元數采用20,快拍數為200,信噪比SNR=0 dB。第一個信源的角度為-1°,第二個信源的角度在第一個的基礎之上以0.1°的速率進行增加。真實的信源間隔應該是一條直線。由于MUSIC算法不能處理相關信源,所以只對本文算法和CS-MUSIC算法的性能進行比較。從圖4中可以看出:本文算法能夠分辨的角度間隔是0.5°,而CS-MUSIC算法能夠分辨的最小的角度間隔為0.7°;并且在角度間隔小于0.5°的條件下,本文算法的性能優越于CS-MUSIC。 通過以上仿真實驗可以得出,本文提出的新的混合范數的方法的確提高了來波方位的估計性能。并且針對不同的信號進行了分析,因此,本文所提算法在實際的情況下也能對信號進行來波方位估計。 本文提出基于混合范數的來波方位估計方法。該方法利用壓縮感知稀疏恢復的混合l1,2范數對噪聲子空間和信號子空間進行稀疏恢復,得到一種新的高分辨率的來波方位估計方法。仿真結果表明,在非相干信源和相干信源的條件下,本文算法性能優于MUSIC和CS-MUSIC算法。但是,本文算法的測向性能仍然不能達到克拉美羅界,同時當角度間隔小于0.5°時,本文算法不能精確地分辨出兩個信號;并且,本文算法需要預估計信源數,而且陣元數要多于信源數。對于信源數未知的情況下,在下一步的研究中可以在DOA估計之前,先利用最新的信源數目估計算法對來波數目進行精確地估計,然后再利用本文所提的算法對信號的來波方位進行精確恢復。 [1]Shaghaghi M, Vorobyov S A. Subspace leakage analysis and improved DOA estimation with small sample size[J]. IEEE Transactions on Signal Processing, 2015,63(12):3251-3265. [2]蔡晶晶,宗汝,蔡輝.基于空域平滑稀疏重構的DOA估計算法[J].電子與信息學報,2016,38(1):168-173. [3]時潔,楊德森,時勝國,等.基于壓縮感知的矢量陣聚焦定位方法[J].物理學報,2016,65(2):1-11. [4]黃麟舒,察豪,葉慧娟,等.均勻線陣目標到達角估計的壓縮感知方法研究[J].通信學報,2015,36(2):1-7. [5]沈志博,董春曦,黃龍,等.一種基于稀疏分解的窄帶信號頻率估計算法[J].電子與信息學報,2015,37(4):907-912. [6]李喆,桑海風,徐維華.欠定非線性系統極小二范數解的可信誤差界[J].吉林大學學報(理學版),2015,53(3):414-418. [7]伍飛云,周躍海,童峰.基于近似零范數和混合優化的壓縮感知信號快速重構算法[J].自動化學報,2014,40(10):2145-2150. [8]Qaisar S, Bilal R M, Naureen M, et al. Compressive sensing : from theory to application[J]. Journal of Communications and Networks,2013,15(5):443-456. [9]閆鋒剛,沈毅,劉帥,等.高效超分辨波達方向估計算法綜述[J].系統工程與電子技術,2015,37(7):1465-1475. [10]Majumdar A, Ward R K, Aboulnasr T. Algorithms to approximately solve NP Hard row-sparse MMV Recovery problem: Application to compressive colcor imaging[J]. IEEE Journal on Emerging and Selected Topics in Circuits and Systems,2012,2(3):362-369. [11]趙擁軍,李東海,趙闖,等.寬帶陣列信號波達方向估計理論與方法[M].北京:國防工業出版社,2013:99-107. [12]Wu X, Deng W, Yang Q. DOA estimation based on MN-MUSIC algorithm[J]. Journal of Information and Computational Science, 2014,11(8):2611-2620. [13]羅鵬飛,張文明,劉忠,等.統計信號處理基礎-估計與檢測理論[M].北京:電子工業出版社,2011:23-29. DOA Estimation Based on Mixed-Norm Algorithm XIE Qianpeng, WANG Lunwen (Electronic Engineering Institute of PLA, Hefei 230037, China) In order to solve the poor performance of the traditional MUSIC algorithm and CS-MUSIC algorithm DOA estimation in the condition of coherent and incoherent sources, an approach based on Mixed-Norm of compressive sensing was proposed in this paper. The proposed method used the characteristics of MUSIC and compressive sensing sparse recovery to obtain the support of the signal domain, then the noise subspace and signal subspace were obtained by the support of the signal domain. Finally, an approach was obtained based on the combination the signal subspace and noise subspace with classical MUSIC algorithm. Simulation experimental results proved that the proposed method had superior performance than MUSIC and CS-MUSIC algorithm under the condition of incoherent source. At the same time, the algorithm‘s angular resolution was also superior to CS-MUSIC algorithm under the condition of coherent source. DOA estimation, CS-MUSIC, compressive sensing, mixed-norm 2016-9-23 國家自然科學基金項目資助(61273302) 謝前朋(1991—),男,河南鄲城人,碩士研究生,研究方向:智能信號處理。E-mail:13721038905@163.com。 TN911.7 A 1008-1194(2017)01-0071-052 基于混合范數的來波方位估計方法
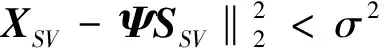
3 實驗驗證
4 結論

