基于改進LPSO混合算法的多機器人編隊

仇國慶+牛婷+寇倩倩

摘 要：針對領航跟隨法和基于行為法在機器人編隊控制上的缺點，采用了混合編隊方法即動態偏轉角度φ值的虛擬領航跟隨法結合基于行為法，能彌補傳統領航跟隨法的缺陷，可以保持隊形的穩定，形成隊形反饋，在兩種編隊方法結合的基礎上，加入混合算法進行在線優化，該混合算法是在PSO算法的基礎上改進慣性權重公式，加速收斂速率和解決易掉進局部最優的缺陷；同時引入能進行長短離搜索的萊維飛行，該混合算法能進一步加快粒子跳出局部最優，避免陷入早熟的情況，從而有效的優化機器人編隊的路徑，可以使機器人的編隊時間縮短。實驗仿真成果證實，所采用的方法的可行性和有用性。

關鍵詞：編隊控制；粒子群算法；慣性權重；萊維飛行

引言

近年來，多機器人編隊控制[1]是已經成為多機器人協作的重要研究方向之一。編隊控制[2]是指機器人以一定的隊形避開環境的約束向目標點運動的控制技術，很多學者根據任務需求，提出許多經典方法，包含有領航跟隨（leader-follower）[3-4]基于行為法（behavior-based）[5]、人工勢場法[6]、虛擬結構法（virtual-structure）等。文獻[7]在虛擬領航者的基礎上加入分散控制算法，但是仍然無法保證隊形的穩定性，文獻[8]提出特定領航者的編隊方法，但是該算法要在一定的充分條件和收斂區間才能發揮作用，文獻[9]提出了改進的人工勢場法的編隊控制，通過沿墻導航法來控制機器人的隊形變換，機器人無法到達最優路徑，上述研究雖然都可以完成機器人的編隊控制，但是很少會在線對機器人的路徑做優化。

針對上述問題，提出了一種用萊維飛行算法結合慣性權重對數遞減的粒子群算法來進行多機器人編隊控制，該方法的思想是當領航者的角度發生變化時，跟隨者能適應其角度的變化，不會發生掉隊的現象，隊形保持穩定，同時對粒子群算法的公式做改進，以對數遞減函數做粒子群算法的慣性權重，可以使收斂速度有一定的提高，萊維飛行的引入，可以增加種群的搜索能力，避免早熟，得到最佳的機器人路徑。

1 混合編隊控制

1.1 基于動態φ值的虛擬領航跟隨法

由于領航跟隨法比較簡單、容易理解，所以就受到研究編隊控制人員的青睞，它的主要原理[10]是選取當中某個機器人作為leader，另外剩余的機器人作為follower，設定領航者（leader）和跟隨者（follower） 運動位置關系，然后follower以固定的距離和方向跟隨leader，形成一定的隊形。但是這種方法太依賴于領航者，一旦領航者出現故障，那么機器人編隊的隊形就無法保持，且該方法無法形成反饋和只能求解局部最優而不是全局最優。動態偏轉角度φ值的虛擬領航跟隨法能彌補其缺點，所示當領航者遇到阻礙，偏轉角度太大，跟隨者可以自適應的改變自己的角度，迅速到達隊形點。

1.2 基于行為法

基于行為法[11]是有幾個子行為組成，它有明確的隊形反饋。但是也存在著一些不足，沒有固定的數學模型，導致行為難以融合，即機器人躲避障礙物的時候和向目標點移動有可能很難同時進行，所以隊形的穩定性就無法控制。

1.3 混合編隊方法

針對前面所述的兩種方法的優缺點，本文提出了動態偏轉角度 φ值的虛擬領航跟隨法，同時結合基于行為法的機器人編隊控制，兩者之間相互互補，完成編隊任務。

當領航機器人遇到障礙物時，會改變其原有的方向，如果偏轉角度過大，會使跟隨者產生掉隊或者回退的現象，采用動態偏轉角度φ值的虛擬領航跟隨法，可以使跟隨者始終和領航者保持相同的偏轉角度φ，產生相同的弧形，穩定隊形，同時在動態偏轉角度φ值的虛擬領航跟隨法上加入基于行為法，可以防止機器人進入死鎖狀態，通過基于行為法的隨機擾動行為和通向目標點的行為，使機器人脫離死鎖，形成完整的隊形。

2 改進的LPSO（Levy Particle Swarm Optimization）算法

2.1 改進的PSO（Particle Swarm Optimization）算法

式中β為對數調整因子，取1.2。K為當前代次數，對數遞減的ωi的變化是先減少緩慢后加速減小，因此它可以使全局和局部的搜索能力有所改善，并加速收斂速度和提高收斂精度。

二是對改進適應度函數，它在算法中占有很高的地位，其性能可以反映粒子本身的好壞程度，本文所采用的就是在機器人原本路徑的基礎上加入穩定度因子、光滑度因子，最后對所有的參數進行加權平均，其公式：F=α×f1+β×f2+γ×f3，α、β、γ分別為的加權因子，可以通過調節α、β、γ來決定各自函數占的比重，且它們都是大于或者等于零，且小于1的實數。f1為機器人的路徑長度，f2為穩定函數，與粒子直線到目標點遇到障礙物的個數有關，f2=M，M是一個較大的為起點到終點的直線路徑上的障礙物之和，f3路徑光滑度函數，f3=πr+πr，n1為機器人在原始方向上改變為45度的次數之和，n2為在原始方向上改變為90度的次數之和，r為機器人的半徑。f1在公式中占有的很高的地位，因此α的取值就比較高，f2其次，β就比α低一個數量級，f3幾乎可以不考慮，γ為接近或者等于0，仿真試驗中α為0.9，β為0.09，γ為0.001。

2.2 萊維飛行

Levy飛行是服從Levy分布的隨機搜索路徑[13]，既能進行短距離也能進行長距離的搜索，現很多優化的領域都已在使用，主要原因是因為它不僅能擴大搜索的范圍，也可以增加種群的多樣性，因此采用萊維飛行能跳出局部最優點[14]。

2.3 混合算法的機器人編隊控制

在機器人編隊控制中，引入萊維飛行的改進的PSO混合算法，可以使機器人避免陷入局部極小點，并迅速找到最優解，機器人能找到一條最優路徑到達目標點，混合算法優化機器人編隊的步驟：

Step1：初始化種群，包括各參數N、x、v、Tmax；

Step2：計算適應度函數F，找到每個粒子的局部最優和整體最優；

Step3：根據具有對數遞減的慣性權重粒子群公式更新粒子的位置和速度；

Step4：粒子更新迭代的次數是否大于10，如果大于10，則執行Step5，否則執行Step6；

Step5：進行萊維飛行算法，重復Step2 和Step3；

Step6：判斷迭代的次數，如若大于Tmax，則程序結束，否則轉向Step2。

3 仿真成果和分析

為了檢驗本文所采用算法的具體效果，在VC6.0的基礎上對其進行仿真測試，在7×7的仿真測試環境下，并與傳統的MPLA編隊算法進行比較分析。

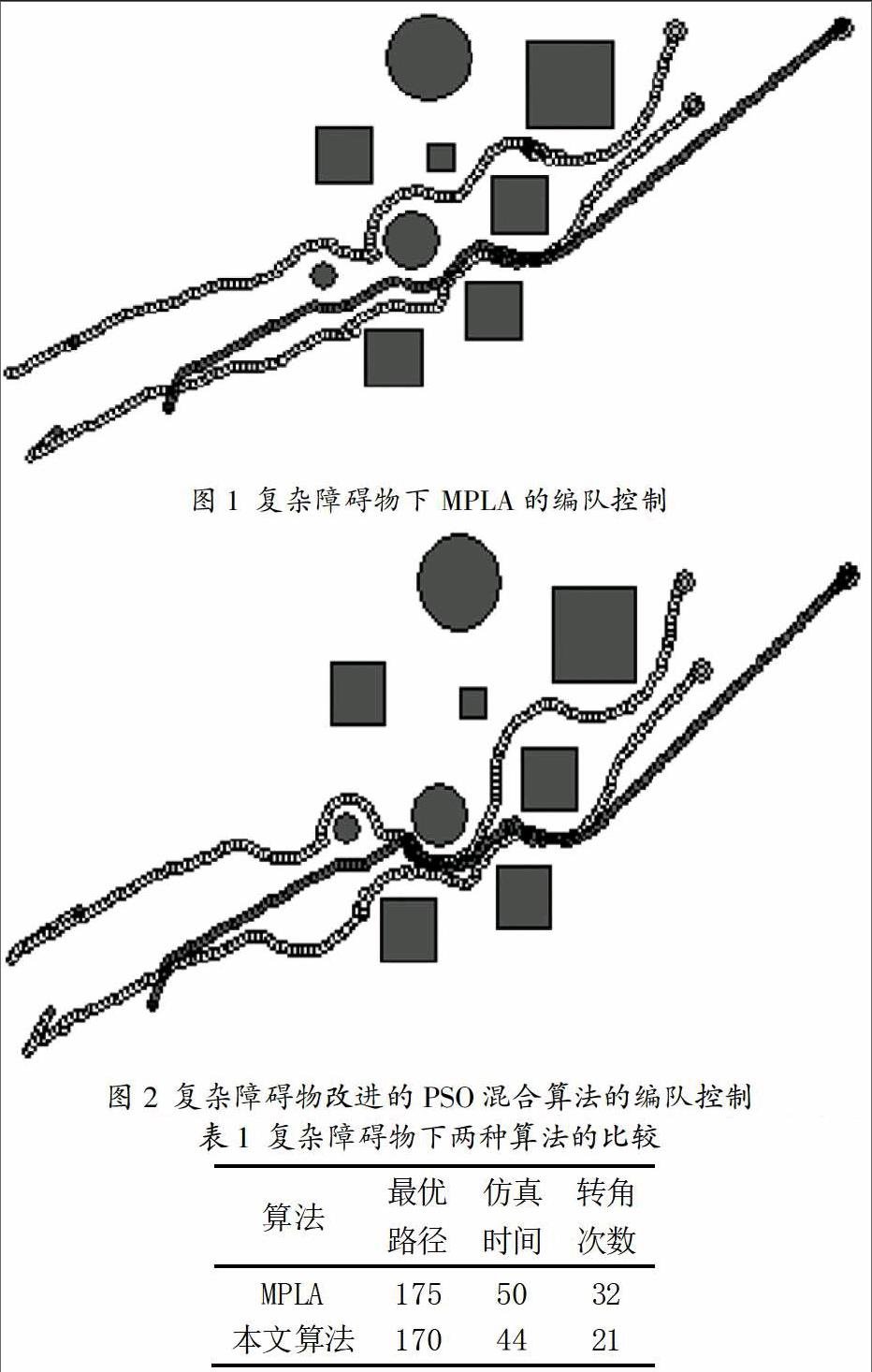
MPLA算法[15]是在傳統的LFB編隊的基礎上，加入多智能體粒子群算法（MAPSO），MAPSO是將多個Agent智能體與PSO算法結合，引入鄰居的概念，加強粒子與其他粒子的相互通信，改變粒子本身的行為，使其多樣性增加，同時利用鄰居間的信息完成搜索到最優值。以下是兩種算法的比較仿真圖，這兩種算法在多個復雜障礙物中的仿真結果如圖1和圖2。圖中矩形和圓形分別代表障礙物，黑色的點代表領航機器人。

在兩種算法中，設定機器人以三角形的隊形開始運行，仿真過程中，機器人可以迅速到達三角形的隊形點，躲避障礙物完成編隊，但是兩種算法相比較，從仿真圖可以看出機器人在簡單障礙物和復雜障礙物的情況下，機器人所走的路徑不同，在改進的LPSO算法下，機器人的路徑得到優化，因此本文所采用算法的編隊路徑效果優于MPLA算法。

為了更好的表現所采用算法優越性，表1記錄了簡單障礙物和復雜障礙物下的兩種算法的性能指標，即路徑長度、仿真時間和轉角次數。

由表1可以看出，本文所采用算法的轉角次數少，機器人路徑的穩定性和光滑性得到提高，同時隊形保持的效果更為明顯，在運動過程中，不會出現多次的拐角震蕩，保持穩定的隊形向前移動；仿真時間少于MPLA算法，可見其收斂速度快于MPLA，機器人能迅速到達目標點，完成編隊的效率也有所提高；機器人所走的路徑步數也不同，且本文算法的路徑步數小于MPLA算法的步數，證實改進的LPSO算法能使機器人選擇最佳路徑，使其到達目標點所走的步數少，獲得的最優路徑也比MPLA短。

4 結束語

把動態偏轉角度φ值的虛擬領航跟隨法，與基于行為法相結合，形成隊形反饋，可以減少掉隊和保持隊形，在編隊控制中，本文采用對慣性權重和適應度函數做改進的PSO算法對路徑規劃，并在此基礎上引入萊維飛行，加快收斂速度，跳出局部極值，得到最優路徑。實驗仿真研究表明，本文算法能使機器人很快找到最優路徑到達最終點，達成編隊要求。

參考文獻

[1]韓光勝，韓佳彤.多機器人編隊的研究與實現[D].北京：北京工業大學，2010.

[2]董勝龍，陳衛東，席裕庚.多機器人編隊的分布式控制系統[J].機器人，2000，22（6）：433-438.

[3]Yu W W， Chen G R， CAO M. Distributed leader- follower flocking control for multi-agent dynamic a systems with time varying velocities[J].Systems and Control Letter，2010，59（9）：543-552.

[4]Ren D H， Lu G Z. Consideration on formation control[J].Control and Decision Making， 2005 2005，20（6）：601-606.

[5]FRESLUND J，MATARIC M J. A general algorithm for robot formations using local sensing and minimal communication robotics and automation[J].IEEE Transactions on Robotics and Automation，2002，18（5）：837-846.

[6]楊麗，曹志強，譚民.不確定環境下多機器人的動態編隊控制[J].機器人，2010，32（2）：283-288.

[7]高芹，鄭新娟，鐘毅，等.基于PSO算法虛擬Leader的多機器人的編隊控制[J].武漢理工大學學報，2014，36（2）：136-140.

[8]杜柏陽，張良國，孫一杰，等.基于特定領航者的多機器人編隊控制方法[J].電光與控制，2015，22（9）：72-76.

[9]周自維，周冰，趙雪.基于改進人工勢場的多機器人編隊控制[J].科技創新與應用，2015，33.

[10]付帥. 動態環境下的多機器人編隊控制方法的研究[J].計算機仿真，2014，31（12）：384-387.

[11]瞿勇，宋業新，張建軍.一類模糊多目標雙矩陣對策的粒子群優化算法[J].海軍工程大學學報，2009（3）：6-11.

[12]楊嬌，葉春明.應用新型螢火蟲算法求解Job-shop調度問題[J].計算機工程與應用，2013，49（11）：213-215.

[13]Yang X S. Nature-inspired metaheuristic algorithm[M].2nded.Frome：Luniver Press，2010：16-29.

[14]王慶喜，郭曉波.基于萊維飛行的粒子群優化算法[J].計算機應用研究，2015，33.

[15]唐賢倫，劉念慈，鄧露，等.基于MAPSO的混合式多機器人編隊控制[J].華中科技大學學報（自然科版），2015，43（7）：104-107.

作者簡介：仇國慶（1963-），男，重慶人，副教授，碩士，主要從事現場總線控制、智能儀器儀表及控制裝置、運動控制系統。

寇倩倩（1991-），女，晉運城人，碩士研究生，主要研究方向：交通流的數據挖掘。