三維空間中線結構光與相機快速標定方法

陳文亮，董清亮，劉 峰，王向軍，吳凡路

?

三維空間中線結構光與相機快速標定方法

陳文亮，董清亮，劉 峰，王向軍，吳凡路

（天津大學微光機電系統技術教育部重點實驗室，天津 300072）

針對結構光立體視覺系統快速標定問題，本文提出了一種多線結構光單目視覺測量系統的快速標定方法，該方法可以同時完成多個線結構光的標定，不必每一個線結構光單獨標定，從而實現相機與線結構光的快速標定。具體為相機內參采用張氏標定法提前標好，外參標定采用設計的三維陣列立柱靶標配合實現。在已知三維陣列立柱靶標各立柱端面中心點對應物像坐標后，可得到二者間的旋轉和平移矩陣；在線結構光投射到對應不同高度立柱端面上后，根據以上物像關系可得到端面光條坐標，利用該坐標可擬合出激光平面方程，進而可建立起各激光面與相機之間的變換關系，完成系統標定。

三維陣列立柱靶標；線結構光；相機標定；平面方程

0 引言

常見的視覺測量系統有雙目測量系統、基于結構光的單目視覺測量系統以及基于點光源的測量系統[1]。其中線結構光單目視覺測量技術具有結構簡單、精度較高、速度快等優點，并且在在線測量、三維地貌測量等領域有廣泛的應用，所謂的線結構光是指面激光。本文就基于線結構光單目視覺測量中的標定進行研究。標定的參數包括攝像機的內外參以及線結構光平面方程，其中攝像機的內參包括焦距、中心點坐標、徑向畸變、切向畸變，都以像素為單位，外參包括平移矩陣與旋轉矩陣，表示像平面坐標系與世界坐標系之間的關系。

在線結構光標定中，由于線結構光平面不同于機械平面，很難確定線結構光平面上某點的世界坐標系下的坐標。所以對線結構光進行標定具有一定的困難。針對線結構光的標定方法主要有細絲散射法[2]和鋸齒靶標法[3]等。但這幾種方法需要精密的輔助設備，而且過程比較復雜，不適合現場標定。Huynh等提出基于三維靶標的交比不變標定方法[4]，該方法精度較高，但標定過程中難以獲得高質量標定圖像。此外現在有利用輔助激光的棋盤格靶標標定方法[5]、基于圓形靶標的線結構光標定方法[6]，這些方法操作復雜，不利于現場標定。裘祖榮，陳培芬等人提出一種多線結構光標定方法[7]，但該方法是用于小測量區域，而且對世界坐標系與激光傳感器的相對位置有一定的要求。本文提出了一種多線結構光單目視覺測量系統的快速標定方法，在該標定方案中，相機的內參采用張正友的標定方法。相機的外參標定與線結構光標定均采用三維陣列立柱式靶標。同時該靶標能夠解決線結構光平面上點難以獲取得問題，該種靶標制作簡單，擺放方便，適合現場標定。

1 線結構光測量數學模型

線結構光測量的數學模型如圖1所示，其中c-ccZc為攝像機坐標系，o-oo為計算機坐標系，-為像平面坐標系。設為線結構光與被測物體的某一交點，在世界坐標系下的齊次坐標為w＝(w,w,w, 1)T，在攝像機坐標系與計算機坐標系下的對應點的齊次坐標分別為c，p2，該點在像平面坐標系下對應點的坐標為￠＝(,, 1)T，根據透視變換[8]，可得：

*￠＝**w＝*w(1)

式中：矩陣,分別為相機的內參與外參，為一任意比例尺度因子，無特殊含義。設線結構光在世界坐標系下的平面方程如下：

*w＋*w＋*w＝1 (2)

由公式(1)與公式(2)可得到一個四元一次方程組，如下所示：

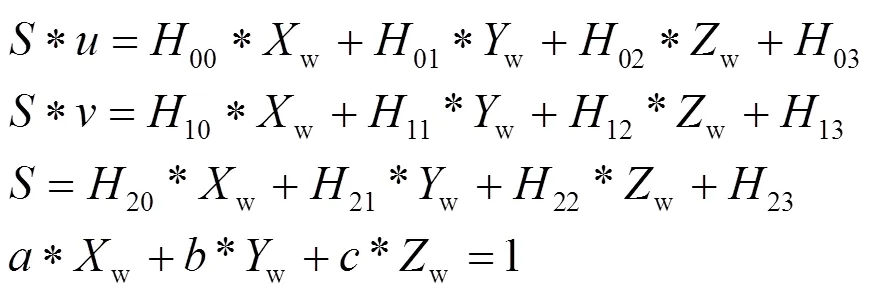
如果攝像機的內參、外參以及線結構光在世界坐標系下的平面方程已知，就可以根據方程組(3)，由線結構光的像平面坐標得到該對應點在世界坐標系下的坐標，如下所示：

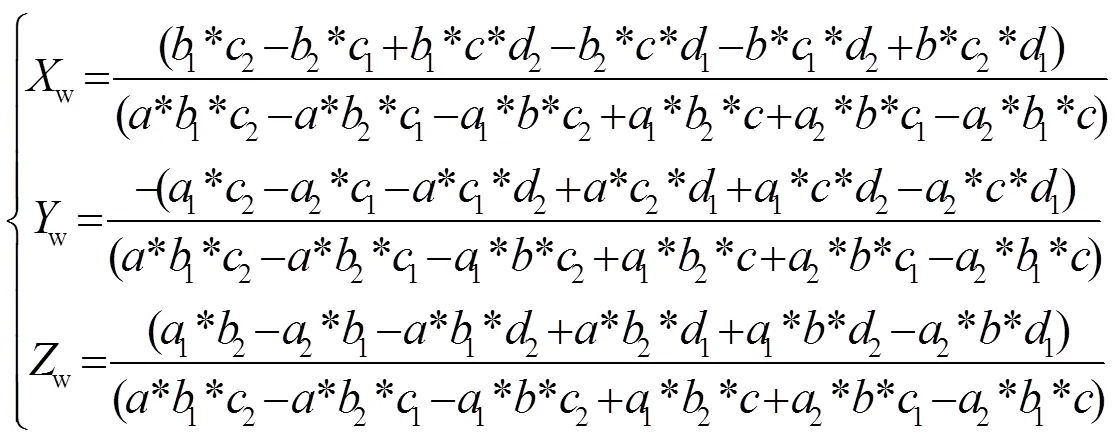
其中：

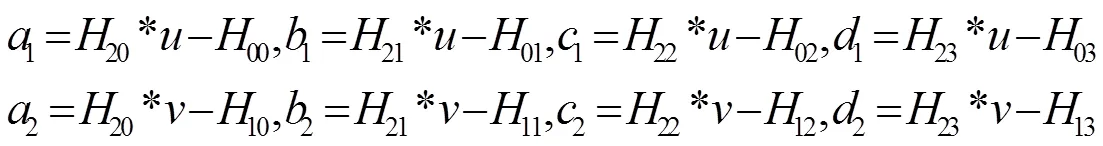
如果能夠同時獲得多個激光面在世界坐標系下的平面方程，每一個線結構光對應一個四元一次方程組，即可同時完成對多個線結構光的標定。

2 相機以及線結構光的標定

2.1 相機內參標定

內參標定采用張氏標定方法，采用棋盤格作為標定靶標，如圖2所示。可以得到相機的焦距、圖像中心點坐標以及畸變系數。由此得到相機內參。

圖2 棋盤格靶標

2.2 相機外參標定

在該方案中，采用三維陣列立柱式的靶標。圖3為標定靶標示意圖。在該靶標中，分布有高低不同的立柱，每一個立柱端面中心點在世界坐標系下的坐標是已知的。在圖像中，可以獲得每一個端面中心點的在像平面坐標下的坐標。通過兩者的對應關系，解得相機的外參。

2.3 線結構光標定

在標定相機外參之前，確保每一條線結構光能夠打在高低不同的立柱上，如圖3所示。這樣，就會在立柱端面有線結構光線條，如圖4所示。

由于已經標定出相機的內參與外參，便可以得到公式(1)，同時每一個立柱的高度是已知的，設立柱的高度為w，則可以通過線結構光線條上點的像平面坐標系下的坐標，通過方程組(6)求得該點在世界坐標系下的坐標：

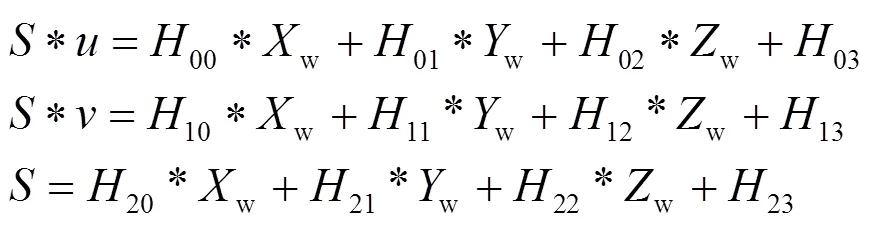
如圖3所示，每一個線結構光在高度不同的立柱端面上形成激光線條，通過方程組(6)求得每一個激光線條上點的世界坐標，然后利用最小二乘法，擬合線結構光平面，得到線結構光在世界坐標系下的平面方程，完成對線結構光的標定。

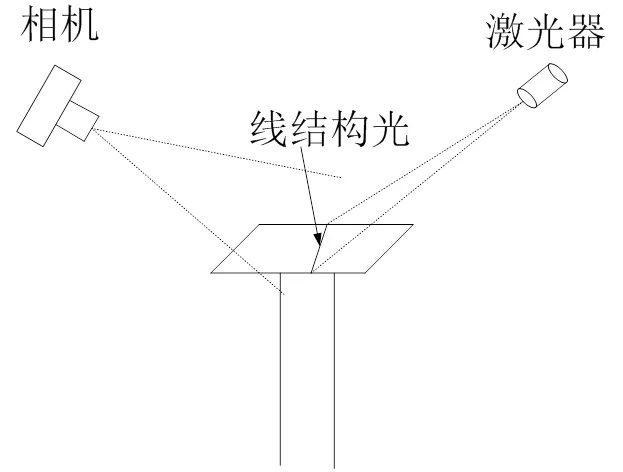
圖4 立柱端面激光線條

3 實驗驗證

在該實驗中，同時對兩條線結構光進行標定，采用的激光器為532nm的綠激光器和650nm的紅色激光器，功率分別為15mW和10mW。實驗采用的為BALSER相機，型號為scA1600-14gm。分辨率為1628×1236，CCD尺寸為1/1.82，像素尺寸4.4mm×4.4mm。

3.1 相機內參標定

采用MATLAB相機標定箱對相機的內參進行標定，在視場不同位置取圖片，如圖5所示。一共取了60幅棋盤格圖片進行標定，標定的結果如表格1所示，其中u、v、0、0單位為像素。1，2為徑向畸變，1，2為切向畸變。

3.2 相機外參標定

在標定外參時，需要特定的三維陣列立柱靶標，在該實驗中，通過在光學平臺上擺放立柱，構成標定所需要的三維陣列立柱靶標，如圖5所示。標定外參時，需要圖片上點的像素坐標以及對應點在世界坐標系中的坐標。其中對應點的世界坐標由三坐標測量機測得，三坐標測量機的測量精度為15mm。當完成測量后，對靶標取圖片，通過讀圖片，獲得對應點的像素坐標。這樣就得到了立柱端面中心點的世界坐標與像素坐標。通過兩者之間的對應關系來獲得旋轉矩陣與平移矩陣。該靶標共有12個立柱，每一個線結構光對應六個立柱，其中的4個立柱用來標定，另外兩個用來做精度校驗。

標定得到的旋轉矩陣與平移矩陣分別為矩陣(7)與矩陣(8)：

圖5 棋盤格圖片位置

表1 相機標定結果

3.3 線結構光標定

然后對擺放的立柱取圖片，立柱擺放如圖6所示。其中每一個線結構光對應有不同高度的6個立柱，每一條線結構光分別打在對應的高度不同的立柱上。其中4個立柱用來擬合線結構光平面，另外兩個立柱作為精度校驗柱，真值由三坐標測量機測得。完成相機內外參標定之后，就可以得到公式(1)，由于每一個立柱的高度是已知的，這樣，就能夠通過立柱端面上線結構光的像素坐標，通過方程(6)，得到線結構光線條上點在世界坐標系下的三維坐標。得到不同高度立柱上點的坐標后，利用最小二乘法，便可以完成線結構光的平面擬合，擬合的平面方程如下：

0.671×10－3×＋0.130×10－1×－

0.300×10－1×＝1 (9)

0.145×10－3×＋0.511×10－2×－

0.102×10－1×＝1 (10)

其中公式(9)為第一條線結構光在世界坐標系下的平面方程。公式(10)為第二條線結構光在世界坐標系下的平面方程。

4 精度評定

完成線結構光的標定之后，每一條線結構光都對應一個方程組(3)，這樣，就可以通過像平面坐標系下的坐標，求得世界坐標系下的坐標。然后，通過兩個校驗柱，對每個線結構光標定結果進行精度校驗，數據如表2與表3所示。其中的真值用三坐標測量機測得。其中相對誤差為0.57%。

圖6 實驗現場圖片

5 結論

該文中提出的多線結構光單目視覺測量系統的快速標定方法，分為相機內參標定，相機外參標定，線結構光標定。其中相機的內參采用棋盤格靶標進行標定，相機的外參與線結構光均采用三維陣列立柱靶標進行標定。三維陣列立柱靶標制作擺放方便，結構簡單，解決了線結構光上的點的世界坐標難以獲取的問題，并采用最小二乘法擬合線結構光平面。實驗結果證明：相對誤差為0.57%。

表2 第一條線結構光實驗兩個校驗點測量結果

表3 第二條線結構光實驗兩個校驗點測量結果

[1] 張勇斌, 盧榮勝, 費業泰, 等. 基于十字線結構光視覺測量系統[J]. 計算機測量與控制, 2004, 12(1): 13-14.

ZHANG Yong-bin, LU Rong-sheng, FEI Ye-tai, et al. Vision Inspecting System Based on Cross Structured Light[J].. 2004, 12(1): 13-14.

[2] 崔希民, 李聰, 袁得寶, 等. 基于拉絲法的線結構光視覺測量系統標定[J]. 科技導報, 2014, 32(24): 65-67.

CUI Xi-min, LI Cong, YUAN De-bao, et al. Calibration of a Line Structured Light Vision Measuring System Based on the Drawing Method[J]., 2014, 32(24): 65-67.

[3] 段發階, 劉鳳梅, 葉聲華. 一種新型線結構光傳感器結構參數標定方法[J]. 儀器儀表學報, 2000, 21(1): 108-110.

DUAN Fa-jie, LIU Feng-mei, YE Sheng-hua. A New Accurate Method for the Calibration of Line Structured Light Sensor[J]., 2000, 21(1): 108-110.

[4] 王金橋, 段發階, 伯恩, 等. 線結構光掃描傳感器結構參數一體化標定[J]. 傳感器學報, 2014, 27(9): 1197-1120.

WANG jin-qiao, DUAN Fa-jie, BO En, et al. Calibration of Line Structured Light Scanning Sensor Structure Parameter Integration[J]., 2014, 27(9): 1197-1120.

[5] 陳新禹, 馬孜, 陳天飛. 線結構光傳感器模型的簡易標定[J]. 光學精密工程, 2012, 20(11): 2347-2350.

CHEN Xin-yu, MA Zi, CHEN Tian-fei. Calibration model for Line Structured Light Vision Sensor[J]., 2012, 20(11): 2347-2350.

[6] 裘祖榮, 陳培芬, 李杏華. 多線結構光視覺傳感器測量系統的標定[J]. 半導體光電, 2014, 35(5): 890-893.

QIU Zu-rong, CHEN Pei-fen, LI Xing-hua. Calibration of Measurement System for Multi-Vision Sensor[J]., 2014, 35(5): 890-893.

[7] 王向軍, 王晶, 劉峰, 等. 野外大視場雙目視覺物體定位監測系統的單參數快速標定[J]. 光學精密工程, 2013, 21(10): 2665-2667.

WANG Xiang-jun, WANG Jing, LIU Feng, et al. Fast Calibration for Binocularvision measuring system with a large field[J]., 2013, 21(10): 2665-2667.

[8] 張曉龍, 劉英, 孫強. 高精度非致冷長波紅外熱像儀的輻射標定[J]. 中國光學, 2012, 5(3): 235-241

ZHANG Xiao-long, LIU Ying, SUN Qiang. Radiometric calibration of uncooled long-wave infrared thermal imager with high-precision[J]., 2012, 5(3): 235-241.

Fast Calibration Method of Multiple Line Structured Light and the Camera

CHEN Wenliang，DONG Qingliang，LIU Feng，WANG Xiangjun，WU Fanlu

(,,300072,)

In order to realize fast calibration of the line structured light in the stereo vision, a calibration method for multiple line structured light of monocular vision measurement was proposed. In this method, the internal camera parameters were determined based on Zhenyou Zhang’s camera calibration. And the extrinsic camera parameters can be got by using the three-dimensional arraycolumn target. The rotation matrix and the translation matrix were got when the center points of the upright columns of the three-dimensional array target and the pixel coordinates were known; after the line structured light projects on the head face of the upright columns, the relation between the object and the image can be got, and then the plane equation can be fitted. After that, the relation between the line structured light and the camera would begot, then the calibration was finished. Experimental results indicate that itsrelative error is about 0.57%.

three-dimensional array column target，line structured light，calibration of camera，plane equation

TP391

A

1001-8891(2017)01-0081-05

2015-09-09；

2017-01-12.

陳文亮（1977-），男，副教授，研究方向：應用光譜。