某航炮緩沖器性能結構優化研究

粟小龍，周長軍，李 勇，王開政，申亞琳

(西北機電工程研究所，陜西 咸陽 712099)

某航炮緩沖器性能結構優化研究

粟小龍，周長軍，李 勇，王開政，申亞琳

(西北機電工程研究所，陜西 咸陽 712099)

通過對某航炮自動機緩沖器結構中影響后坐力的彈簧剛度、彈簧預壓量、液壓阻尼系數等主要參數進行優化分析，基于Matlab編程，解算分析了某航炮自動機的后坐復進運動，求得了最大后坐位移約束條件下的最大后坐力優化解。結果表明：自動機最大后坐位移與最大后坐力是相互制約的兩個因素，僅僅通過結構參數優化難于達到預期目標；在最大后坐力滿足要求時，使得后坐位移增大超出預期。研究結果為緩沖器結構設計參數選取提供了參考。

緩沖器；航炮；參數優化；后坐力

某航炮自動機武器系統裝載應用于某飛行器，為了增強在戰場上的對抗能力和提高掌握戰場優勢的水平，必須增大航炮的火力威力(射速、彈丸威力等)，但也不可避免地增加了后坐力和后坐位移。因此，要使飛行器綜合能力得到提高，必須在保證火力威力等指標前提下，盡可能減小后坐力。減小后坐力的裝置有：炮口制退器和緩沖器，其中緩沖器發揮主要作用。現有的彈簧液壓緩沖器以其結構簡單、緩沖性能穩定的優勢,在航炮自動機上得到廣泛應用。筆者通過對某航炮自動機緩沖器結構中影響后坐力的主要參數如彈簧剛度、彈簧預壓量、液壓阻尼系數等參數進行優化分析，基于Matlab編程，解算分析了某航炮自動機的后坐復進運動，求得了最大后坐位移約束條件下的最大后坐力優化解。

1 自動機運動解析

建立自動機動力學模型，為便于分析，對全炮和液壓緩沖器作以下合理假設[1]：

1)除彈簧外各構件均作剛體處理。

2)自動機沿身管軸線做平面運動。

3)忽略彈簧內耗。

4)緩沖器內摩擦力項只考慮由緊縮量產生的摩擦力。

5)液壓油不可壓縮，且流動為一維定常流。

1.1 后坐運動解析

航炮自動機后坐運動由3個階段組成：內彈道時期后坐、后效期后坐和慣性后坐[2]。炮箱內結構由外能源提供動力來運動，所以自動機的后坐復進運動相對獨立，在自動機運動平面內，各個時期對應的后坐運動微分方程分別為

(1)

(2)

(3)

式中：y為自動機后坐位移，以擊發前自動機初始位置為后坐原點，沿身管軸線向后為正；S為膛內橫截面積；m為自動機后坐質量；kb為緩沖彈簧剛度；y0為緩沖彈簧預壓量；uh為后坐液壓阻尼系數；Ff為炮箱導軌摩擦力和緩沖器內摩擦力之和；y為內彈道時期炮膛合力修正系數；pn為平均膛壓，由內彈道方程解算所得的離散壓力數據；Fph為后效期炮膛合力，由后效期相關參數算得。

通過Matlab編程解(1)～(3)3個二階運動微分方程，利用龍格-庫塔法ode45求解器[3]，為便于計算分析取射角α=0。解算過程中需注意：式(1)中需要先將表格數據的pn導入程序并進行匹配求解計算時間步長的插值；式(2)中Fph由彈丸出炮口時的膛壓和后效期特征量結合求得；式(1)末端時間為彈丸出炮口時間tg；式(2)末端時間為后效期結束時間點tk；式(3)起始時間為tk，末端時間需要通過一次插值判斷后坐速度等于0來確定。

1.2 復進運動解析

復進運動可表示為

(4)

式中：y1表示從后坐終了點開始的復進運動行程距離；L為由后坐運動解算獲得的最大后坐位移，故(L-y1)表示自動機相對后坐原點的后坐位移，進行以后坐位移y為自變量的代換y=L-y1,可得復進運動微分方程為

(5)

式中：uf為復進時液壓阻尼系數；m、y0、Ff、α等參數意義不變。

求解復進運動方程時，需注意：式(5)初始時間為后坐運動結束時間，而復進結束時間點需要通過一次插值判斷復進到達自動機后坐原點，此時y等于0。

基于自動機的受力分析，結合運動微分方程式(1)～(5)，可將后坐過程和復進過程后坐力大小F分別表示為

(6)

(7)

根據該航炮自動機各已知參數，以及現有的緩沖器參數kb=65 N/mm、uh=200、y0=170 mm，仿真求解可獲得一個射擊循環中后坐力隨時間變化的曲線和后坐位移和后坐速度隨時間變化的曲線，如圖1、2所示。

該仿真計算求得的最大后坐力為13.30kN，最大后坐位移27.54mm；而實物樣機射擊試驗測試結果為最大后坐力13.8kN，最大后坐位移28.8mm。兩項誤差分別為3.75%和4.38%，在允許范圍內。但最大后坐力值明顯大于項目指標要求，研究過程中期望實現的指標是：在不同射速下，最大后坐力F≤12.5 kN，最大后坐位移ymax≤28.5 mm。所以需對自動機后坐問題進行參數優化分析，為結構改進設計提供理論支持，以實現期望指標。

2 結構參數改進分析

2.1 液壓阻尼器模型

有研究者提出緩沖器阻尼器為孔隙式時，輸出阻尼力為[4]

Fz=C×vn

(8)

式中：C為阻尼器阻尼系數，與小孔大小、個數、流體介質有關，并對阻尼力影響較大；n為流體介質的流動指數；v為速度。

為獲得現有航炮緩沖器的C和n，對現有緩沖器進行試驗，將測試結果進行擬合求得n=2。因為通過結構設計使得緩沖器在后坐與復進時流液孔面積不同，從而有著不同的液壓阻尼系數。試驗結果擬合得后坐時阻尼系數uh為200，復進時阻尼系數uf為90 000。

2.2 液壓阻尼器結構

緩沖器內的液壓阻尼裝置結構如圖3、4所示，后坐與復進時緩沖器內的變化是流液孔個數的改變導致流液孔面積的不同，簡化求解得后坐液壓阻尼和復進液壓阻尼系數分別為

(9)

(10)

式中：a為單向活門個數；A1為活塞桿內腔流液孔面積；A2為單個單向活門流液孔面積；K為簡化表示的綜合系數。

射擊過程中，當后坐液壓阻尼系數較大時，會使得后坐力變化的平臺效應較差，所以往往希望通過結構設計使得uh值較小。

2.3 參數尋優計算

綜上所述，以所編寫的求解程序為基礎，進行以彈簧剛度kb、彈簧預壓量y0、后坐液壓阻尼系數uh和復進液壓阻尼系數uf為變量參數的改進研究[5]，該問題的數學表達為

minF(y)y∈Rn

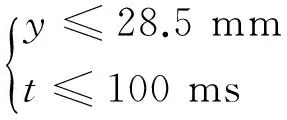
(11)

以最大后坐力F為主要目標，將后坐位移ymax作為條件約束，同時顧及自動機后坐復進運動循環時間t不大于100 ms，否則當射速高于600發/min且為連發射擊工況時，可能會出現前沖現象導致最大后坐力和后坐位移不斷累加。

考慮到緩沖器結構尺寸的適裝性和工藝合理性，計算參數變化范圍為：60≤kb≤90、150≤y0≤190、120≤uh≤225。在此區間內，通過變量代換kb′=kb/5、y0′=y0/5、uh′=uh/15將離散優化問題轉化為關于kb′、y0′和uh′的整數規劃問題，通過Matlab編程求解，得到對應參數下的最大后坐力和后坐位移，如圖5所示。

每一個波形對應一個彈簧剛度，隨著k值增大，后坐力波形逐漸往上，即最大后坐力逐漸增加，后坐位移波形往下，即后坐位移逐漸減少。圖5中上部的直虛線表示ymax=28.5 mm的期望值，下部的點劃線表示F=12.5 kN的期望值。滿足條件的數據是后坐力值取在點劃線下方，同時后坐位移值取也在直虛線下方。結果表明：基本沒有同時滿足F≤12.5 kN和ymax≤28.5 mm的組合，即沒有最優解，參數調整過程中，在

條件下，得

這與F≤12.5 kN和ymax≤28.5 mm的指標要求比較接近。實現后坐力的再減少必然導致后坐位移的明顯增大。圖6～8具體展現了kb、y0、uh單獨變化時后坐力及后坐位移大小的變化規律，充分說明了減小最大后坐力和減小后坐位移存在的矛盾性，這與物理認知相符。

通過對圖6～8分析可知，后坐力和后坐位移的變化滿足此消彼長的規律，減小后坐力的代價往往是后坐位移的增大。另外，后坐力和后坐位移對彈簧剛度的變化敏感性較高，這與后坐過程中彈簧勢能轉變量是自動機能量消耗的主要部分有關；而對液壓阻尼系數的變化敏感性較低，這與對后坐液壓阻尼系數取值變化區間較小有關。

綜合可得：液壓彈簧式緩沖器雖然結構簡單，但僅靠參數改進的結構優化難以做到兼顧實現期望的后坐力、后坐位移目標，只能在有限范圍內協調后坐力大小和后坐位移大小的矛盾，尋求次優的平衡點。

2.4 理論估算驗證

從動量守恒和能量守恒出發，通過一定的估算，旁證上述參數優化分析的合理性。能量動量轉換公式為

(12)

式中：E為內彈道階段結束時自動機具有的動能；I為內彈道階段結束時自動機具有的動量，大小為I=I1-I2，I1為火藥燃氣作用下的炮膛合力總沖量，I2為預壓力反向沖量。

I1可由炮膛合力對時間求積分獲得，經計算，該自動機炮口制退器效率使得后效期炮膛合力沖量遠小于內彈道期炮膛合力沖量，且約等于0，為簡化計算，忽略其影響。I2可由現有緩沖器所取預壓力F及內彈道時間t估算可得，大小為I2≈Ft。

用s表示限定的后坐運動的位移，要通過后坐力消耗掉能量E，在后坐力保持定值時能使后坐力的最大值取到最小，該定值也是最大后坐力的理論最小值，用FR表示。代入s=28.5mm等相關數據，求得FR=E/s≈12.65kN。

可見，期望的指標很接近理論極限，只要火藥燃氣能量只作用于自動機的后坐與復進運動，沒有其他形式的消耗，那么不管進行怎樣的參數優化調整，都不能實現期望值。估算會存在一定量的誤差，但總的來說，仍能給緩沖器結構改進作出指導。

3 結束語

針對某航炮自動機后坐力大的問題，采用Matlab編程，解算自動機后坐復進運動，模擬計算結果與試驗結果基本相符。在不改變緩沖器結構形式前提下，一定范圍內選取彈簧剛度、彈簧預壓量、液壓阻尼系數這3個主要影響后坐復進運動的參數值，期望通過參數尋優達到期望的目標值。模擬計算結果表明現有緩沖器結構形式不能兼顧實現期望的最大后坐力和后坐位移，要想獲得更小的后坐力，不可避免地引起后坐位移較大的變化。同時理論估算指出，期望的目標值與理論極限值接近，使得很難通過改進緩沖器結構設計來實現。要提高緩沖性能，除了實現單發特定后坐力和后坐位移期望值，還要將連發時緩沖器的緩沖狀態作為性能指標，這一結論為今后緩沖器設計提供參考。當單發后坐力及后坐位移無法進一步優化時，如何實現連發時的穩定收斂浮動以改善后坐性能值得研究。

)

[1]姚養無.架座武器后坐力測試技術研究[J]．測試技術學報，2010,24(2):124-127．YAOYangwu.Studyonthemeasuretechnologyofrecoilforceformountedweapon[J].JournalofTestandMeasu-rementTechnology,2010,24(2):124-127. (inChinese)

[2]高躍飛．火炮反后坐裝置設計[M]．北京：國防工業出版社，2010：30-55，160-170． GAO Yuefei. The design of gun recoil system[M]. Beijing：National Defence Industry Press,2010:30-55，160- 170. (in Chinese)

[3]薛定宇，陳陽泉．高等應用數學問題的Matlab求解[M]．3版．北京：清華大學出版社，2013：205-210，237-249. XUE Dingyu, CHEN Yangquan. Advanced applied mathematical problem solutions with Matlab[M]. 3th ed. Beijing: Tsinghua University Press,2013：205-210，237-249. (in Chinese)

[4]陳威．粘滯阻尼器的理論和實驗研究[D]．武漢：華中科技大學，2012． CHEN Wei. Theoretical and experimental researches on a viscous damper[D]. Wuhan：Huazhong University of Scie-nce and Technology,2012. (in Chinese)

[5]李鵬，陳永才，狄長春．輕武器用小型緩沖器結構改進與優化[J]．火炮發射與控制學報,2012(4):34-37. LI Peng, CHEN Yongcai, DI Changchun. Improvement and optimization of small buffer used by small arms[J]. Journal of Gun Launch & Control,2012(4):34-37. (in Chinese)

A Performance and Structural Optimization Study of Aircraft Gun Recoil Damper

SU Xiaolong,ZHOU Changjun,LI Yong,WANG Kaizheng,SHEN Yalin

(Northwest Institute of Mechanical & Electrical Engineering , Xianyang 712099, Shaanxi, China)

By optimizing and analyzing the main parameters on the gun automaton in buffer structure of recoil spring stiffness and pre compression spring and hydraulic damping coefficient, The recoil and counterrecoil movement of a gun automaton were analysed, based on Matlab programming.And the optimization solutions of maximum recoil were obtained under the constraint of given recoil displacement. The results show that the maximum displacement and maximum recoil force are two factors mutually restricted each other, so only by optimizing the structure parameters is difficult to reach the expected goal;while the maximum recoil force meets the requirement, the recoil displacement increases more than expected. The results provide a reference for the selection of design parameters of buffer structure.

recoil damper; aircraft gun; parameters optimization; recoil force

10.19323/j.issn.1673-6524.2017.01.006

2016-09-03

粟小龍(1991—)，男，碩士研究生，主要從事火炮自動機技術研究。E-mail：459815670@qq.com

TJ303+.4

A

1673-6524(2017)01-0028-05