基于特征模型的高超聲速飛行器再入多約束預測控制
張 軍,李亞輝,朱晟楨
(1.江蘇大學 電氣信息工程學院,江蘇 鎮江 212013;2.中國運載火箭技術研究院,北京 100191)
基于特征模型的高超聲速飛行器再入多約束預測控制
張 軍1,李亞輝2,朱晟楨1
(1.江蘇大學 電氣信息工程學院,江蘇 鎮江 212013;2.中國運載火箭技術研究院,北京 100191)
針對存在輸入和輸出多約束的高超聲速飛行器再入控制問題,提出了一種基于特征模型的魯棒預測控制方法。對耦合的非線性再入動力學采用低階線性特征模型簡化,設計魯棒預測控制器保證滿足再入控制的多約束。基于特征模型的低階等價性,將再入動力學的輸入輸出動態特性用線性時變的特征模型描述,并將三通道姿態耦合和干擾作為廣義復合干擾。將灰色理論中累加求和的思想引入到特征模型參數辨識算法中,弱化了再入隨機噪聲的影響,通過灰色辨識方法在線估計特征模型的時變參數和干擾。設計一種基于線性矩陣不等式(LMI)滾動優化技術的H2/H∞魯棒預測控制律與基于灰色辨識的補償器共同構成復合控制器,保證了整個閉環系統的穩定,滿足輸入和輸出約束。數據仿真驗證了算法的有效性。
高超聲速飛行器;約束;特征模型;魯棒預測控制;灰色辨識
高超聲速飛行器具有響應快速、機動能力強等特點,是未來國防裝備的重要發展方向,其中再入控制系統設計最為復雜。在高超聲速飛行器的再入過程中,運行環境復雜,飛行器飛行高度和飛行馬赫數變化范圍大,飛行器的氣熱特性、氣動特性發生劇烈變化,造成再入動力學模型具有快時變、非線性耦合、強干擾等特性[1-2]。傳統的PID控制很難使再入系統具有良好的閉環控制性能,這給再入控制器的設計帶來了困難和挑戰[3-4]。更值得注意的是,高超聲速飛行器在再入過程中存在再入過程(動壓、過載、熱流)、執行結構等約束,導致姿態控制系統存在控制和狀態等多約束,即舵機的偏角、氣流系角、角速度等,違反了這些約束,再入控制系統性能和穩定性將受到嚴重的惡化[5-6]。
目前,動態逆控制、變結構控制、神經網絡控制等方法提高了再入系統魯棒性[7-9],但系統的輸入和輸出約束很少明確考慮。雖然采用高增益控制器的非線性控制和魯棒控制能保證系統具有良好的閉環性能,卻忽略了噪聲放大和需要更大控制能力的問題[4],若考慮約束則原有的控制性能和穩定性就會受到破壞,控制律需要重新設計。目前,抗飽和控制方法、輸入信號調節方法、預測控制等方法是解決約束控制的主要方法,文獻[10]將抗飽和控制和輸入參考信號調節2種方法組合起來有效解決輸入約束,但是有一定的保守性,只有發生飽和行為時,抗飽和補償器才執行,影響再入的高精度控制和強機動性能,并且不能處理輸出約束。因此,需要在再入控制系統的高性能要求和滿足約束之間進行有效折中。
預測控制具有反饋校正、模型預測、滾動優化等特點,能有效處理系統化多約束,逐漸被航天控制所關注[11-12]。文獻[13]采用精確反饋線性化將再入非線性模型轉化為線性模型,通過滾動優化機制解決再入飛行器的輸入和輸出約束,但是控制約束轉化成非線性約束,計算仍然復雜,并且要求系統模型實時可逆。為了簡化計算量,文獻[14-15]在高超聲速飛行器的上升段、再入段制導中設計了連續時變預測控制器,但沒有考慮魯棒性。預測模型是影響預測控制應用的關鍵因素,若把原有的多耦合、強非線性再入動力學模型直接作為預測模型,在線計算量很大,不能滿足高實時性要求。文獻[16]提出的特征模型用低階線性單入單出時變差分方程來描述高超聲速飛行器復雜動力學特性,形式簡單,工程運行方便,對象特征模型與實際對象輸出是等價的,在工程上得到成功應用。文獻[17]設計了基于特征模型的自適應控制系統,采用了黃金分割控制律,分析了閉環系統的穩定性。文獻[18]主要考慮飛行器平穩滑翔過程中滾動角保持為零的條件下,基于特征模型設計簡化的自適應控制律。但是對于大角度再入機動的情況,偏航和滾動通道強耦合信息和非線性干擾不能簡單忽略,再入特征模型需要考慮這一因素。
基于特征模型的低階等價性,將再入動力學的動態特性用線性時變的特征模型描述,并把三通道姿態耦合和外來干擾作為廣義復合干擾,對復雜的再入動力學進行簡化建模。利用灰色預測中“累加生成”的優點,重新生成辨識數據,增強了辨識數據的規律性,通過灰色辨識在線估計特征模型的時變參數和干擾。在此基礎上,設計H2/H∞混合預測控制指標,基于LMI滾動凸優化獲得魯棒預測控制律,保證了整個閉環系統的穩定,滿足系統狀態和輸入約束。
1 再入飛行器動力學模型和問題描述
忽略地球自轉、曲率、風、氣動舵面等因素對飛行器動力學的影響,高超聲速飛行器再入動力學模型為[4]
(1)
(2)
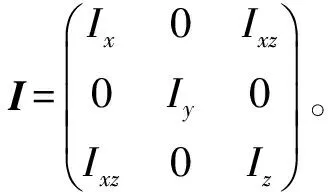
①舵偏角輸入飽和約束。
|δa|≤δa,max,|δe|≤δe,max,|δr|≤δr,max。
②輸出約束。
|α(k)|≤αmax,該約束保證了再入飛行器具有良好的氣動特性和溫度分布,降低了防熱要求。
|ωx|≤ωx,max,|ωy|≤ωy,max,|ωz|≤ωz,max,角速度約束保證了飛行器的結構和力學安全要求。
再入姿態控制系統的任務是:在滿足上述輸入和輸出約束的情況下,控制系統跟蹤制導系統給出的攻角、滾動角指令,控制穩態精度小于0.5°,同時側滑角保持為0。
2 再入動力學特征模型
再入動力學系統(1)和系統(2)是強非線性、時變、不確定的多變量耦合系統,直接設計控制器比較困難。基于文獻[16]系統的特征模型輸入輸出等價原則,對系統(1)、系統(2)的控制輸出α,β,φ求二階導數,進行等價代換和泰勒級數近似展開,得到輸入輸出時變的二階攻角離散模型:
α(k+1)=fα1(k)α(k)+fα2(k)α(k-1)+
g1(k)δα(k)+Δα(k)
fα1+fα2≈1,δα≈δe
(3)
β(k+1)=fβ1(k)β(k)+fβ2(k)β(k-1)+
g2(k)δβ(k)+Δβ(k)
fβ1+fβ2≈1,δβ≈δr
(4)
φ(k+1)=fφ1(k)φ(k)+fφ2(k)α(k-1)+
g3(k)δφ(k)+Δφ
fφ1+fφ2≈1,δφ≈δa
(5)
式中:fα1,fα2,g1為攻角通道的特征模型時變參數;δα,δβ,δφ為三通道的等效控制輸入;fβ1,fβ2,g2為側滑角通道的特征模型時變參數;fφ1,fφ2,g3為滾動角通道的特征模型時變參數。模型(3)~模型(5)是單入單出的時變系統,明顯降低了原始再入動力學的復雜性。Δα(k)是攻角通道的廣義擾動,包含其他特征通道的動態耦合信息、外部干擾,反映了再入飛行器的三通道強耦合、非線性、時變性,在飛行器大角度機動時該量不能忽略,這是與文獻[16-17]的不同之處。定義:
Δα(k)=m11β(k)+m12φ(k)+Δα1(k)
(6)
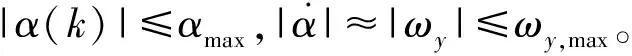
3 再入特征模型的灰色辨識
高超聲速飛行器的再入特征模型是時變的單入單出系統,需要線辨識模型參數。而再入狀態中含有近似均值為0的白噪聲,影響辨識精度。目前,灰色預測的數據累加生成可有效弱化原始序列中隨機噪聲因素的影響,增強了數據的規律性,這里采用灰色辨識估計特征模型的參數fα1(k),fα2(k),g1(k),m11(k),m12(k),Δα1(k),具體步驟如下[18]。
(7)
進行一次累加生成(式中:m為采樣數據數目),得到規律更強的新序列,消除隨機噪聲的影響,作為辨識的輸入數據:
{X1(1),X1(2),…,X1(N)}
(8)式中:N為灰色序列數據數目,N≥n+1。由上述灰色數據定義得到再入動力學特征模型(3)的灰色模型為
(9)
在辨識時間內,建模誤差和干擾近似認為
令V=(fα1(k)fα2(k)g1(k)m11m12Δα1)T,
(10)
由灰色模型可得:
(11)
為提高再入特征模型控制的魯棒性,這里設計前饋補償控制:
(12)
4 H2/H∞魯棒預測控制
令Δfα1(k),Δfα2(k),Δg1(k)為特征模型系數辨識誤差;Δ為uc(k)補償Δα(k)后的誤差,它們是有界的。此外,由于α(k),δα(k)也是明確的區域約束,因此,參數辨識誤差、未建模動態、外界干擾等因素引起的綜合擾動也是有界的,這里作為廣義擾動,即
d(k)=Δfα1(k)α(k)+Δfα2(k)α(k-1)+
Δg1(k)δα(k)+Δ
灰色辨識補償后的特征模型為
α(k+1)=fα1α(k)+fα2α(k-1)+g1δα1(k)+d(k)
δα=uc+δα1
(13)
x(k+1)=A(k)x(k)+B(k)δα1(k)+Bdd(k)
(14)
對原有系統(1)的約束進行轉化。
①攻角約束轉化為系統(14)的輸出約束:
|α(k)|=|(0 1 0)x(k)|≤αmax
②攻角變化率和飛行器最大角速度約束轉化為系統(14)的輸出約束:
(15)
式中:T為控制周期。
③考慮灰色估計補償器后,新的輸入約束:
u=|uc(k)+δα1(k)|≤δe,max
(16)
|δα1(k)|≤min(|δe,max-uc|,|-δe,max-uc|)=umax
(17)
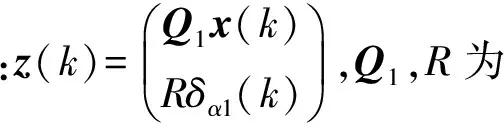
①H∞性能指標。對于任意給定的γ>0,從d(k)到z(k)的傳遞函數滿足:
‖Gzd‖∞≤γ
(18)
②H2性能指標。
(19)
這里采用LMI設計控制器處理輸入和輸出約束,通過Lyapunov理論保證系統(14)的魯棒性能和穩定性。基于H2/H∞性能指標提出如下定理。
定理1 設x(k)是系統(14)在采樣k時刻的狀態測量值,系統采用狀態反饋控制律δα1(k+i)=K(k)x(k+i),F(k)=YQ-1,實現閉環系統魯棒漸近穩定的充分條件是存在變量:b>0,Q>0,滿足如下LMI多約束的優化問題:
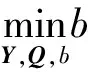
C1=(0 1 0)
證明 選取V(x(k))=xT(k)P(k)x(k),V(x(k+1))=xT(k+1)P(k)x(k+1),定義x(k+i)表示基于x(k)測量在k+i時刻的預測狀態,δα1(k+i)是k時刻第i步預測控制,則控制系統的二次穩定需要滿足:
(20)
由灰色辨識的收斂穩定性知道,補償d(k)趨近于0,存在:
γ2dT(k+i)d(k+i)-zT(k+i)z(k+i)<0。
當M(k)<0時,V(x(k+i+1))-V(x(k+i))<0,當i=∞時,V(x(k+i))趨近于0,將式(20)左右兩邊從i=0到i=∞相加,得到:
(21)
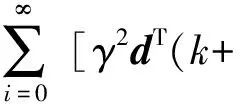
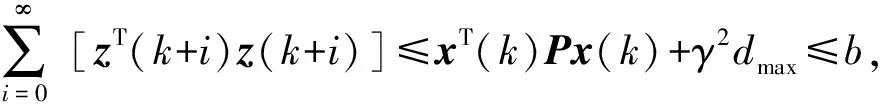
其中,M(k)<0是實現設計目標的充要條件。
(22)
利用Schur補性質,式(22)可以寫成下面的矩陣不等式:
(23)
令Q=bP-1,K=YQ-1,對式(23)分別左乘、右乘diag{b1/2P-1,b1/2I,b1/2I,b1/2I,b1/2I},得到如下不等式:
(24)
H2性能指標式(19)等價如下LMI:
(25)
1)輸出約束分析。
由M(k)<0,因此V(x(k+i+1))≤V(x(k+i)),推導zT(k)Q-1z(k)≤1 是不變集。
(26)
因為‖y(k+i|k)‖2≤ymax,所以
(27)
等價如下不等式:
(28)
因此,攻角約束轉化為
(29)
角速度約束轉化為
(30)
2)輸入約束分析。
灰色前饋補償后的舵偏角約束為
(31)
令K=YQ-1,則δα1=Kx=YQ-1x,不等式(31)可以寫成如下的形式:
(32)
利用Schur補性質,式(32)等效如下的不等式:
(33)
3)算法實現。
本文提出的算法如下:
①基于實時的輸入和輸出數據,利用灰色辨識攻角通道的特征模型參數fα1,fα2,g1,m11,m12,Δα1(k)等;
②利用灰色辨識結果,設計補償器uc補償三通耦合運動信息、未建模信息和干擾Δα1(k);
③計算魯棒預測控制律δα1=Kx,將總的控制u=δα1+uc施加到再入飛行器上;
④重復前面過程 ①。
其他通道控制算法與此類似。
5 仿真研究
針對某面對稱的高超聲速飛行器確定的飛行狀態(αβφ)=(1000)(單位:(°)),獲得相應的特征模型參數范圍,設飛行器的高度為40 km,Ma=10,則其氣動系數的范圍如下[4]:
kxx∈[-0.358 5,-1.434 1],
kxz∈[-0.010 1,-0.015 2],
kyy∈[-0.106 0,-0.294 5],
kzx∈[-0.012 7,-0.050 6],
kzz∈[-0.025 3,-0.038 0],
kxa∈[40.590 9,34.339 5],
kxr∈[3.181 9,3.172 9],
kye∈[25.322 5,22.790 2],
kza∈[2.719 6,2.284 5],
kzr∈[4.536 3,4.133 8]。
假設飛行器姿態角速度的最大值為|ωx|max=|ωy|max=|ωz|max=1.047 rad/s,輸入控制量最大值為30°,采樣時間為0.01 s。
攻角控制通道:
α(k+1)=fα1α(k)+fα2α(k-1)+g1δα(k)+Δα,
fα1∈[1.996 8,2.003 2],
fα2∈[-1.003 2,-0.996 8],
g1∈[2.275 4×10-3,2.536 3×10-3]。
側滑角控制通道:
β(k+1)=fβ1β(k)+fβ2β(k-1)+g2δβ(k)+Δβ,
fβ1∈[1.996 5,2.003 5],
fβ2∈[-1.003 5,-0.996 5],
g2∈[3.376 0×10-4,4.057 7×10-4]。
滾動角控制通道:
φ(k+1)=fφ1φ(k)+fφ2α(k-1)+g3δφ(k)+Δφ
fφ1∈[1.982 3,2.018 1],
fφ2∈[-1.018 1,-0.982 3],
g3∈[3.305 5×10-3,4.195 7×10-3]。
控制系統的要求為側滑角保持在0°附近,攻角跟蹤精度小于0.5°。
1)有時變擾動特征模型的攻角跟蹤。
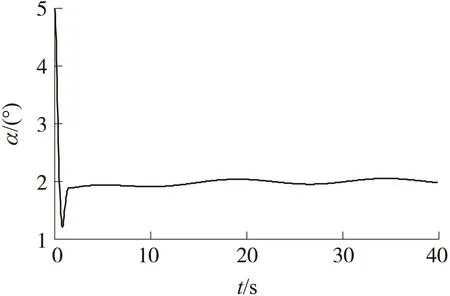
圖1 時變干擾下的攻角跟蹤曲線
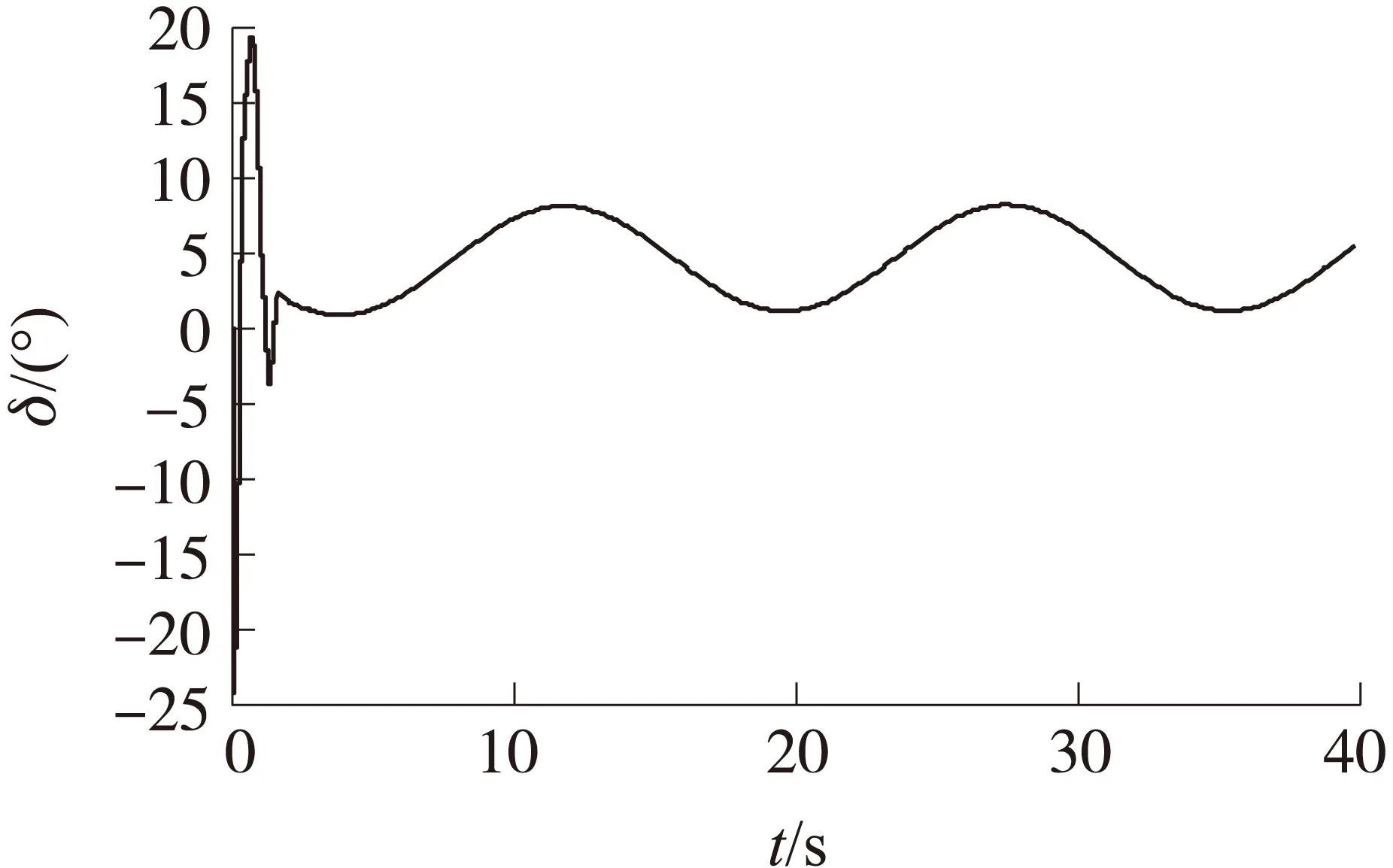
圖2 時變干擾下的控制舵角曲線
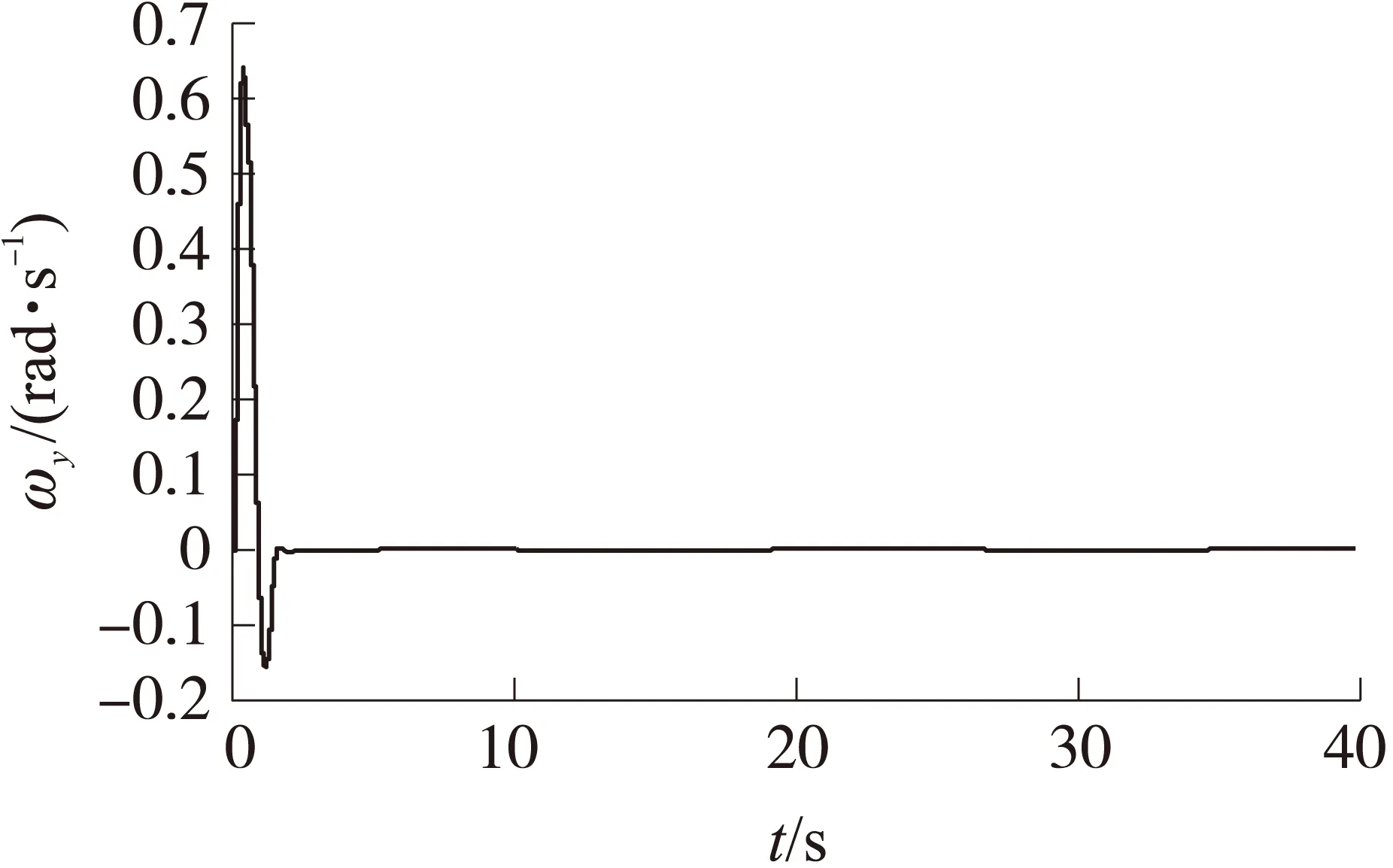
圖3 時變干擾下的角速度曲線
2)隨機噪聲和時變擾動下的攻角跟蹤。
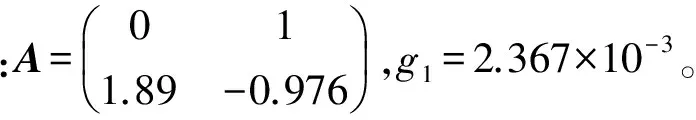
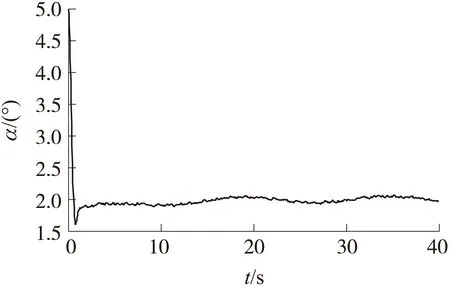
圖4 隨機噪聲和時變擾動下的攻角跟蹤曲線
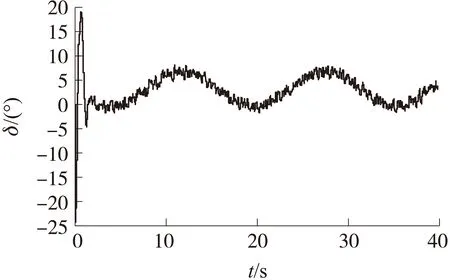
圖5 隨機噪聲和時變擾動下的控制舵角曲線
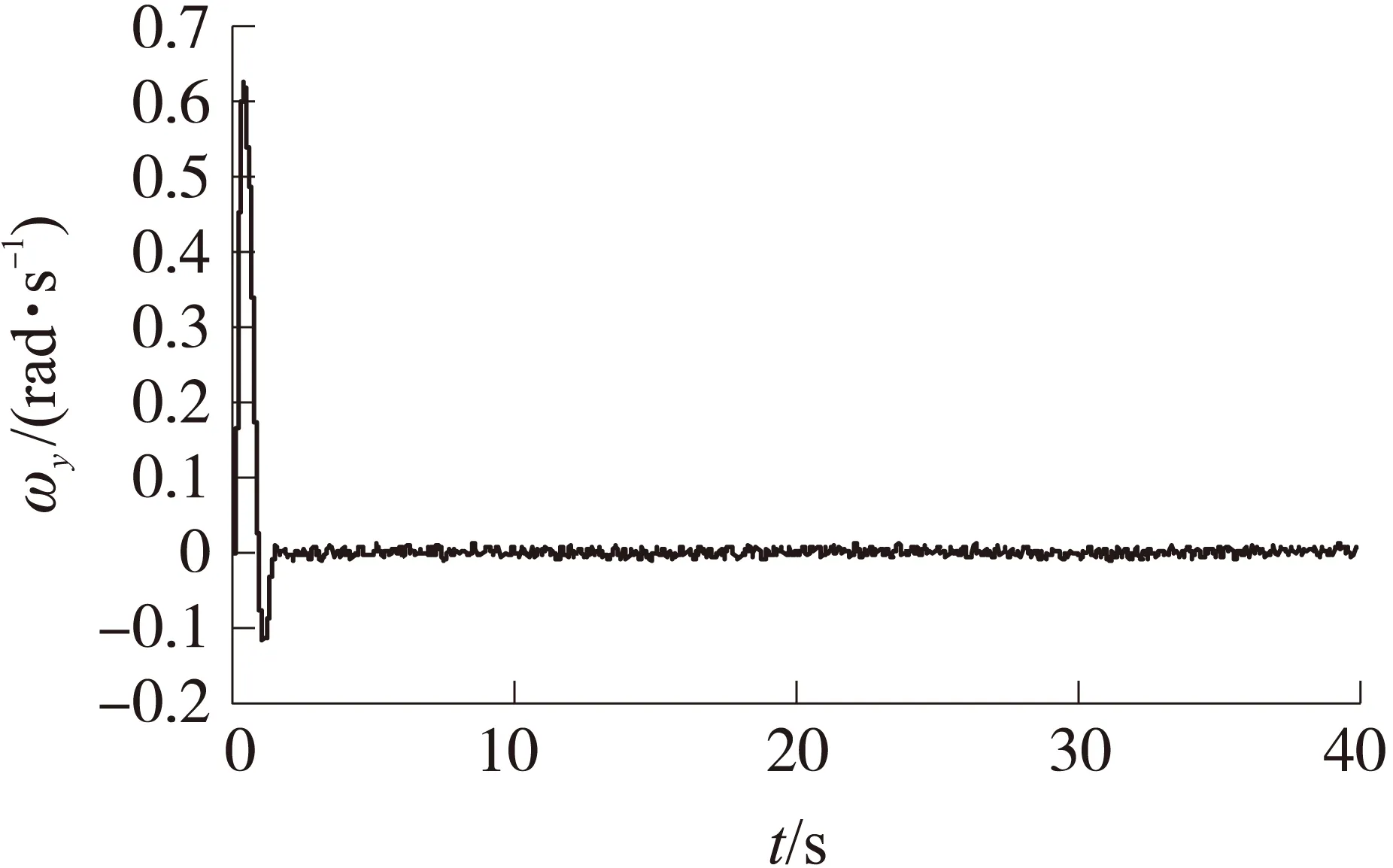
圖6 隨機噪聲和時變擾動下的角速度曲線
6 結論
針對有輸入和輸出約束的非線性再入飛行器動力學模型,基于特征模型設計穩定的魯棒預測控制律。采用時變的特征模型描述再入動力學模型,把三通道姿態耦合和外來干擾作為廣義復合干擾,對復雜的再入動力學進行簡化建模,并通過灰色辨識估計特征模型的時變參數;基于LMI滾動凸優化設計H2/H∞魯棒預測控制律,保證了整個閉環系統的魯棒穩定,滿足系統的輸入和輸出多約束,通過數值仿真驗證了本文算法的有效性。
[1] HARPOLD J.Shuttle entry guidance[J].Journal of the Astronautical Sciences,1979,28(3):239-268.
[2] LU P.Entry guidance:a unified method[J].Journal of Guidance,Control,and Dynamics,2014,37(3):713-728.
[3] WU H,MENG B.Review of the control research of hypersonic vehicle[J].Advances In Mechanics,2009,39(6):756-765.
[4] ZHANG Z,HU J.Stability analysis of a hypersonic vehicle controlled by the characteristic model based adaptive controller[J].Science China:Information Sciences,2012,55(10):2 243-2 256.
[5] SHEN Z J,LU P.On-board generation of three-dimensional constrained entry trajectories[J].Journal of Guidance,Control,and Dynamics,2003,26(1):111-121.
[6] LU P.Regulation about time-varying trajectories:precision entry guidance illustrated[J].Journal of Guidance,Control,and Dynamics,1999,22(6):784-790.
[7] XU B,SUN F,LIU H,REN J.Adaptive kriging controller design for hypersonic flight vehicle via back-stepping[J].IET Control Theory and Applications,2012,4(6):487-497.
[8] CHARLES E H,YURI B S.Sliding mode disturbance observer-based control for a reusable launch vehicle[J].Journal of Guidance,Control,and Dynamics,2006,29(6):1 315-1 328.
[9] YURI B S,CHARLES E H.Reusable launch vehicle control in multiple-time scale sliding modes[J].Journal of Guidance,Control,and Dynamics,2000,23(6):1 013-1 020.
[10] ALICIA Z,ANDREA S.Combined reference governor and anti-windup design for constrained hypersonic vehicles models[C]//AIAA Guidance,Navigation,and Control Conference.New York:AIAA,2009:6 283-6 289.
[11] CHIRISTOPHER P,MORGAN B,ILYA K.Model predictive control guidance with extended command governor inner-loop flight control for hypersonic vehicles[C]//AIAA Guidance,Navigation,and Control Conference and Exhibit.New York:AIAA,2013:5 028-5 048.
[12] ZHANG J,SUN T R.Disturbance observer-based sliding manifold predictive control for reentry hypersonic vehicles with multi-constraint[J].Journal of Aerospace Engineering,2016,230(3):485-495.
[13] VAN W R.Combined feedback linearization and constrained model predictive control for entry flight[J].Journal of Guidance,Control,and Dynamics,2006,29(2):427-434.
[14] BRINDA V,DASGUPTA S.Guidance law for an air-breathing launch vehicle using predictive control concept[J].Journal of Guiance,Control,and Dynamics,2006,29(6):1 460-1464.
[15] WU H X,HU J,XIE Y C.Characteristic model-based all-coefficient adaptive control method and its applications[J].IEEE Transactions on Systems,Man,and Cybernetics-Prat C:Applications and Reviews,2007,37(2):213-221.
[16] XU L J.The hypersonic vehicle control based on the all-channel-coupled characteristic model[J].Aerospace Control and Application,2012,38(4):12-18.
[17] GONG Y L,WU H X.Characteristic model-based adaptive attitude control for hypersonic vehicle[J].Journal of Astronautics,2010,31(9):2 122-2 128.
[18] LIU L,CHEN R W.Modeling algorithm using accumulated generating operation and weighted product[J].System Engineering and Electronics,2010,32(5):976-979.
[19] PATIENCE E,ORUKPE I M.Model predictive control based on mixedH2/H∞control approach[C]//Proceedings of the 2007 American Control Conference.New York:IEEE,2007:11-13.
Predictive Control Based on Characteristic Model for Reentry Hypersonic Vehicle With Multiple Constraints
ZHANG Jun1,LI Ya-hui2,ZHU Sheng-zhen1
(1.Electrical and Information Engineering College,Jiangsu University,Zhenjiang 212013,China; 2.China Academy of Launch Vehicle Technology,Beijing 100191,China)
In order to study the reentry control problem of hypersonic vehicle with multiple constraints,a novel robust predictive-control-method was proposed based on the characteristic model.The low-order linear characteristic model was adopted to simplify the coupled nonlinear reentry dynamics,and the robust-predictive-controller was designed to satisfy the multiple constraints in the reentry control.Based on the low-order equivalence of characteristic model,the input and output dynamic-characteristic of the reentry dynamics was modeled by linear time-varying model,and the three-channel coupling and external disturbance were considered as a generalized composite disturbance.The accumulative sum idea in the grey theory was introduced into the parameter identification of characteristic model,and the effect of random noise factor was reduced,and the regularity of identification data was strengthened.The time-varying parameters and the disturbance were on-line estimated based on grey identification.The mixedH2/H∞robust predictive control-law was proposed by linear matrix inequality(LMI)receding horizon optimization technique,and the compensator of grey identification was feedforward compensated.The closed-loop system is stable,which satisfies the input and state constraints.The validity of the algorithm was verified by simulation results.
hypersonic vehicle;constraints;characteristic model;robust predictive control;gray identification
2016-08-19
國家自然科學基金項目(51379044;51405303;61503158)
張軍(1972- ),男,副教授,博士,研究方向為飛行器控制,預測控制。E-mail:jzhang@ujs.edu.cn。
V249
A
1004-499X(2017)01-0001-08

