基于回歸分析的燕京啤酒凈利潤波動研究

周可瀅

摘 要：隨著改革開放，我國人民生活水平逐年攀升，飲品的新花樣層出不窮，各種飲料和酒類充斥著我們的生活，尤其在大學生聚會中，更是不可或缺的。為此，選取了燕京啤酒作為研究對象，將其凈利潤與影響凈利潤因素的關系進行分析，引進了虛擬變量，在進行多次擬合后建立了四元回歸模型，并對模型中變量的重要性進行了對比分析，同時針對大學生聚會飲酒問題提出了建議。

關鍵詞：燕京啤酒；價格波動；回歸分析；凈利潤

中圖分類號：F27

文獻標識碼：A

doi：10.19311/j.cnki.16723198.2017.02.031

1 背景介紹

改革開放三十幾年，一個顯著的表現就是人民的生活水平越來越高，人們現在追求的多是生活質量，從琳瑯滿目的生活消費品中就可以看出來。其中，飲品更是以迅猛的速度豐富起來，相應的，飲品制造業領域內也呈現出一片欣欣向榮的景象。

從我們當代學生來看，現在的課余生活因為經濟的發展而豐富起來，其中最具有代表性的就是團體活動結束后的聚餐。團體活動結束后，參與活動的成員出去聚餐似乎已經成為了慣例。說到聚餐，就離不開飲料酒類，可謂是無酒不歡，不醉不歸。

酒類公司的凈利潤與經濟的發展關系很密切，但究竟什么原因是其的主導因素。本文以此為出發點，選取了近些年股價波動較大的燕京啤酒作為研究對象，希望能從這一個公司的數據研究中窺到整個酒類公司乃至飲品制造業的情況。

燕京啤酒在世界啤酒產銷量前十名，中國行業百強企業。全國市場占有率達到11%以上，華北市場50%，北京市場在85%以上。燕京啤酒已遍布全國各省市，遠銷美國、意大利、英國、加拿大、澳大利亞等17個國家，出口居全國第3位。在北京，燕京啤酒在餐廳中很常見，北京人常稱呼普通燕京啤酒為“普京”。

燕京啤酒在整個啤酒行業中，名列第二。在2010年中國酒類流通協會、中華品牌戰略研究院共同主辦的，“華樽杯”中國酒類品牌價值評議中，其品牌價值為263.18億，榮膺啤酒類品牌價值第二名。華樽杯酒類品牌價值評議是最有最權威，最專業的無形資產評估。燕京將堅持“發展民族啤酒工業，爭創國際知名品牌”的信念，積極參與國際市場競爭。

燕京啤酒集團一九九六年開始股份制改造，經過一年認真細致的籌備工作，燕京啤酒集團公司于1997年完成了股份制改造，并在半年內獲得了兩個融資渠道：一個是1997年5月參加了北京控股有限公司在香港的紅籌股上市，二是1997年6月25日在深圳證券市場A股上市。燕京啤酒具有A股和紅籌股雙重概念，這種獨特的股權結構使燕京啤酒集團公司可以橫跨大陸與香港兩地證券市場籌資，拓寬了融資渠道，而且燕京啤酒集團公司通過股權置換持有北京控股有限公司6.9%的股份。

本文選取燕京啤酒作為研究對象，首先是因為其為上市公司，有一定的透明度，其次在飲品制造業有一定的影響力。

2 模型介紹

本文采取回歸分析的方法進行分析與建模。“回歸”一詞最早由英國天才科學家Sir Galton（1822-1911）在研究父親與子輩身高的相關性問題是提出。回歸分析是統計學中的一個重要組成部分，它以數理統計為基礎應用性很強，也是最常用的一種統計分析法。它用于探索一組變量之間的關系，尤其是可以用定量的方法描述并解釋變量間的關系，從而進一步估計或預測應變量的值。

回歸分析是最靈活合最常用的統計分析法之一，它用于分析一個因變量與一個或多個自變量之間的關系.特別是用于定量地描述和解釋相互關系以及估計或預測因變量的值。

回歸分析是一種應用很廣泛的數量分析方法。它主要用于分析事物之間的統計關系，側重于考察變量之間的數量變化規律，通過回歸方程的形式描述并反映這種關系，幫助人們準確的把握變量受其他一個或多個變量影響的程度，進而為控制和預測提供一定的科學依據。

2.1 多元線性回歸模型

本文選取的模型：

y=β0+β1x1+……+βkxk+μ

其中被解釋變量Y的變化可以由兩部分解釋，一由解釋變量X的變化所引起的線性部分；二由其他隨機因素引起的變化。βj稱為回歸參數。

2.2 最小二乘估計

本文將采取最小二乘法估計參數。最小二乘原理：根據被解釋變量的所有觀測值與估計值之差的平方和最小的原則求得參數估計量。它是一種使因變量的觀察值與估計值之間的誤差平方和達到最小來求得βj的方法。用最小二乘法擬合的直線來代表x與y之間的關系與實際數據的誤差比其他任何直線都小。

在已經滿足方程基本假設的情況下，多元線性模型結構參數βj的普通最小二乘估計具有無偏性、線性、有效性。同時，隨著樣本容量的增加，參數估計量具有漸近有效性、漸近無偏性、一致性。

2.3 回歸方程的檢驗

2.3.1 經濟檢驗

檢驗模型參數估計量的合理性：檢驗符號，檢驗大小。

2.3.2 擬合優度檢驗

擬合優度檢驗即是檢驗樣本數據點聚集在回歸線周圍的密集程度，用來評價回歸方程的代表程度。對于多元線性模型，構造統計量：

R-2=1-RSS/（n-k-1）TSS/（n-1）

其范圍在0～1之間。該統計量越接近于1，模型的擬合優度越高。

2.3.3 方程的顯著性檢驗：F檢驗

檢驗被解釋變量與所有解釋變量之間的線性關系是否顯著，若用線性描述是否恰當。在多元模型中，即為檢驗模型中的參數βj是否顯著不為0。采用方差分析的方法：TSS=RSS+ESS，認為在總離差平方和中，回歸平方和相對于殘差平方和所占的比例是否較大，若很大，則表示線性關系明顯，反之，則線性關系不明顯。

構造F統計量：

F=ESS/kRSS/（n-k-1）～F（k，n-k-1）

2.3.4 變量的顯著性檢驗：t檢驗

若方程的總體線性關系顯著，但是并不等于其中每個解釋變量對于被解釋變量的影響都是顯著的，所以，必須對每個解釋變量均進行顯著性檢驗，以決定其是否作為解釋變量被保留在模型中。而這一檢驗是由t檢驗完成的。

構造t統計量：

ti=iSi～t（n-k-1）

2.3.5 殘差檢驗

（1）序列相關性檢驗——DW檢驗。

如果隨機擾動項序列的各項之間相關，則稱模型出現了序列相關。本文所用檢驗方法是構造統計量如下：

DW=∑nt=2（et-et-1）2∑nt=2et2≈2（1-） DW∈（0，4）

當DW值越接近2時，μt越接近非自相關。

（2）多重共線性檢驗——方差膨脹因子VIF。

多重共線性即指多個解釋變量之間存在著線性相關關系的現象。本文所用檢驗方法是考察方差膨脹因子VIF，其取值范圍是（1，∞）。如果結果大于或等于10，則說明該解釋變量和方程中其他解釋變量之間存在著嚴重的共線性。

3 實證分析

本文收集到2001—2013年間每個季度燕京啤酒公司凈利潤作為因變量，并選取了國內有效三星及三星以上酒店比例、燕京啤酒資產總計、居民消費水平、肝硬化住院率四個變量作為自變量。

在這里需要說明的是，國內有效三星及三星以上酒店比例意為星級飯店統計管理系統中經營情況數據通過省級旅游主管部門審核的數量比例。因酗酒易導致肝病為常識，故在此選用肝硬化住院率來反映酗酒對健康的傷害。

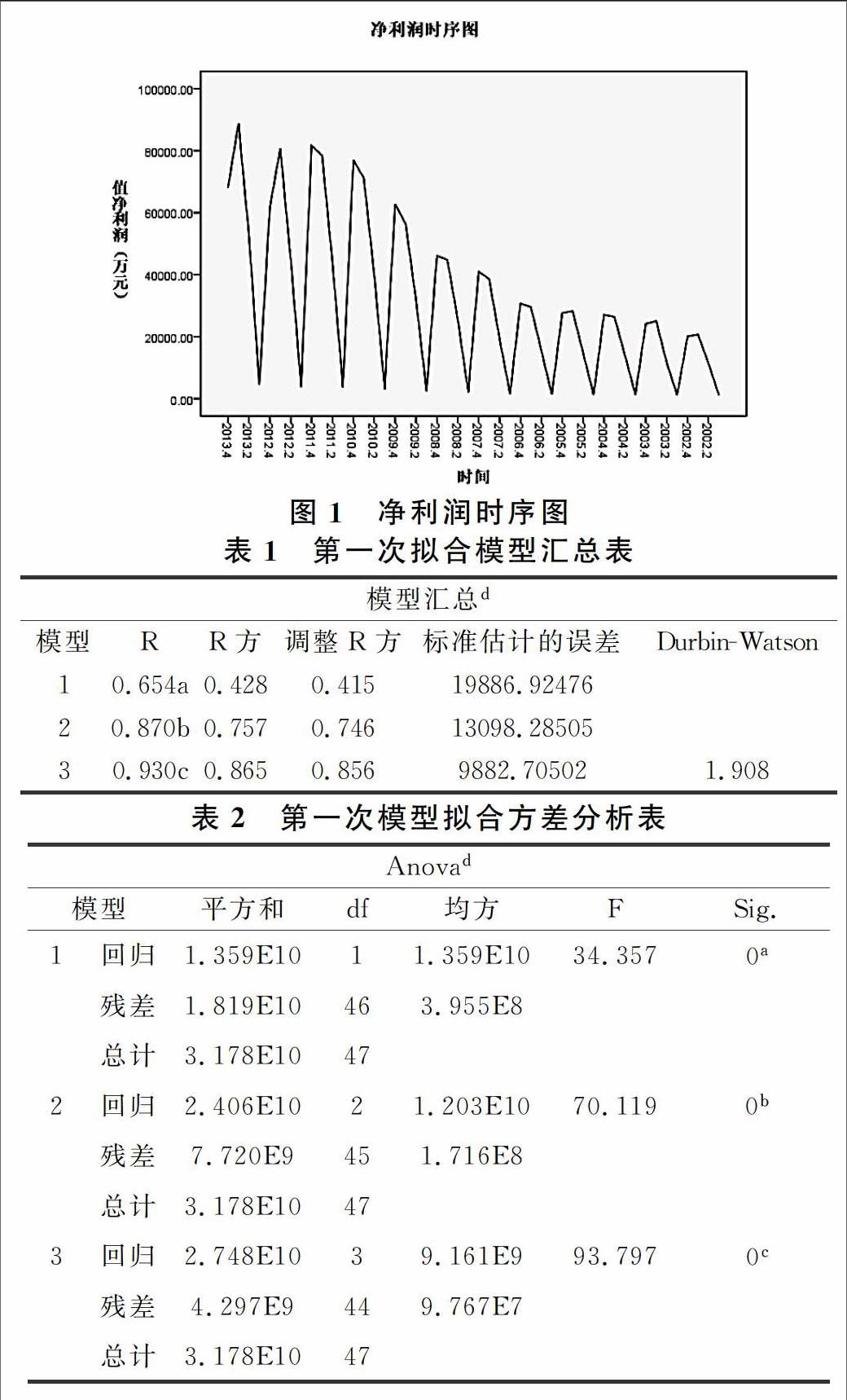
3.1 繪制圖形

由以可以看出，凈利潤的時序圖有很強的周期性，這個可能與春節前期酒類需求量猛增，而春節過后需求量驟減導致的，故引進兩個虛擬變量如下：

D1=1（第一季度）0（其他季度） D2=1（第二季度）0（其他季度）

這里是以第三季度和第四季度為基礎類別。

引進虛擬變量以后，這里就有了6個自變量。繪制虛擬變量以外的變量與凈利潤之間的散點圖可以看出，四個非虛擬變量的自變量分別與因變量之間存在一定關系，除肝硬化住院率與凈利潤沒有顯著的線性關系外，其余三個變量均與因變量有一定的線性關系，考慮到完整性，先嘗試保留肝硬化住院率變量，用六元回歸方程擬合。

3.1.1 六元回歸方程擬合

利用spss軟件，以逐步的方法先嘗試建立六元回歸方程，得到表1。

由模型匯總表格可以看出調整后的R方為0.856，是一個比較滿意的數值，說明模型擬合度較高，DW值為1.908，很接近2，認為μt非自相關。

由方差分析結果看到：F值為93.797，Sig值為0.000<0.05，故認為總體回歸系數顯著不為0。（α=0.05）

由以上逐步進入變量的過程可以看出，最終被保留下來的變量為國內有效三星及三星以上酒店比例與虛擬變量D1、D2，保留下來的三個變量均通過了統計學檢驗，P值均小于0.05，VIF均小于10。而資產總計、居民消費水平、肝硬化住院率三個變量由于不顯著而被舍棄掉。（α=0.05）

由已排除變量表格可以看出，資產總計的VIF為40.745>10，居民消費水平的VIF為11.635>10，說明存在很強的共線性，肝硬化住院率的P值為0.237>0.05，沒有通過統計學檢驗，但其三者的實證意義重要，結合凈利潤的時序圖，嘗試將凈利潤對數化后，再次經行六元線性方程擬合。（α=0.05）

3.1.2 第二次六元回歸方程擬合

先利用spss軟件進行凈利潤的對數化，后以逐步的方法嘗試建立六元回歸方程，得到表5的數據。

由模型匯總表格可以看出調整后的R方為0.994，不僅大于第一個模型的0.856，而且十分接近1，模型擬合度很滿意，DW值為1.521，小于第一個模型的1.908，但是也比較接近2，近似認為μt非自相關。

由方差分析結果看到：F值為1890.483，Sig值為0<0.05，故認為總體回歸系數顯著不為0。（α=0.05）

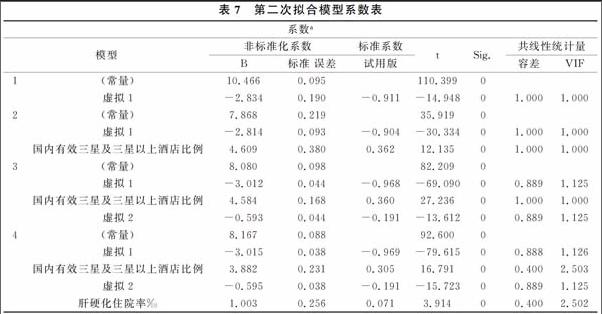
由表7可以看出，最終被保留下來的變量為國內有效三星及三星以上酒店比例、肝硬化住院率和虛擬變量D1、D2。相較第一個模型，多加入了一個肝硬化住院率，但依舊舍棄了資產總計和居民消費水平。

由以上可以看出，該模型中的四個變量P值均小于0.05，VIF值均小于10，都通過了統計學檢驗，可以認為該模型較為滿意。（α=0.05）

3.2 最終模型

綜上所述，最終得到四元回歸模型如下：

ln=8.167+3.882threestars+1.003gyh-3.015D1-0.595D2

其中y是凈利潤；threestars是國內有效三星及三星以上酒店比例；gyh是肝硬化住院率；D1和dum2是虛擬變量。

4 分析結論

4.1 實證意義

因所建最終模型的系數是非標準化系數，參看表3-2-3第二次擬合模型系數表可以發現，國內有效三星及三星以上酒店比例的標準系數為0.305，肝硬化住院率的標準系數為0.071，而虛擬變量D1的標準系數是-0.969。可知影響凈利潤絕對數的最主要原因是季度原因。

從實際看，中國的傳統節日——春節，對酒類公司的利潤影響很大，春節前期，人們往往會購置年貨，在此之前，經銷商和各大商場、超市等就需要進貨，這可能正是在第三、第四季度，公司利潤能有大幅提升的原因。

但是國內有效三星及三星以上酒店比例的影響力度也不可小覷，因為國內三星及三星以上酒店是銷售酒類的主要地點，尤其對高端酒類的銷售影響很大，雖然銷售數量所占份額不是很大，但是其對凈利潤的影響不能稱之為小，其對凈利潤的影響力是大于肝硬化住院率的。

在做第一次六元線性回歸模型擬合時，出現了模型擬合較好但是變量不顯著的情況，在進行殘差檢驗后發現有嚴重的共線性；嘗試對數化凈利潤，但是除了模型的擬合優度更高以外，各個變量依舊沒有通過統計學檢驗；嘗試放棄共線性強的變量，雖然模型擬合度較高，但實證意義表達的不夠完善；最后采用對數化加上放棄共線性較強的變量的方法，雖然依舊放棄了連兩個變量，但是模型已經能通過經濟學檢驗和統計學檢驗，并且較為完善的表達出經濟意義和實證意義。

4.2 建議

由上文的分析和最終模型可以看出，酒類公司的凈利潤是和肝硬化住院率存在一定的正相關的，也就是說，在某種意義上，那些嗜酒如命而因此進醫院甚至為此送命的人們為酒類公司創造了效益。

本文在選取變量時，選取肝硬化住院率來反映酗酒對健康的傷害，但其沒有酒精肝比例更能反映出本文想要表達的意愿，但由于酒精肝比例著實難以獲得，故退而求其次采用肝硬化比例，因為酒精也是造成肝硬化的一大元兇，可以從某種程度上表達出本文想要表達出的意愿。同時，肝硬化住院率的獲取也很困難，本文采用臨近年份的數據替代的方法，可能正因為此，才造成變量不夠顯著，對模型影響力不夠的情況。

參考文獻

[1]謝龍漢.尚濤.SPSS統計分析與數據挖掘[M].北京：電子工業出版社，2012.

[2]張曉峒.計量經濟學基礎（第三版）[M].天津：南開大學出版社，2007.

[3]中華人民共和國國家衛生和計劃生育委員會.2012中國衛生統計年鑒[J/OL].2013，（5）.

[4]中華人民共和國國家旅游局.2002-2013年每季度全國星級飯店統計公報[EB/OL].

[5]中華人民共和國國家統計局.2013年中國統計年鑒[J/OL].2014：223.

[6]姜培紅.影響農藥使用的經濟因素分析——以福建省為例[D].福建：福建農林大學，2005.

[7]龐佳豐.我國手機市場顧客價值影響因素實證研究[D].上海：同濟大學，2006.

[8]尤曉琳，郭衛霞.概率統計在經濟學中的應用[J].安陽工學院學報，2012，（06）：122125.

[9]姜基彬.我國銀行卡市場的多元統計分析[D].上海：華東師范大學，2013.

[10]馬秋芳，孫根年，謝雪梅.基于虛擬變量回歸的旅游花費模型構建[J].統計與決策，2008.

[11]高芳，崔勇.多元線性回歸分析在房地產市場中的應用[J].河南機電高等專科學校學報，2009.