2015年江蘇省高考數學卷第19題閱卷感悟
江蘇省溧水高級中學(211200) 徐茂炳
2015年江蘇省高考數學卷第19題閱卷感悟
江蘇省溧水高級中學(211200) 徐茂炳
一、背景分析
筆者參加了2015年江蘇高考數學閱卷,試題的解法、評分標準、考生的錯誤引發了筆者對數學解題教學的一點思考.所閱的是數學卷第19題,閱卷結果如下表:
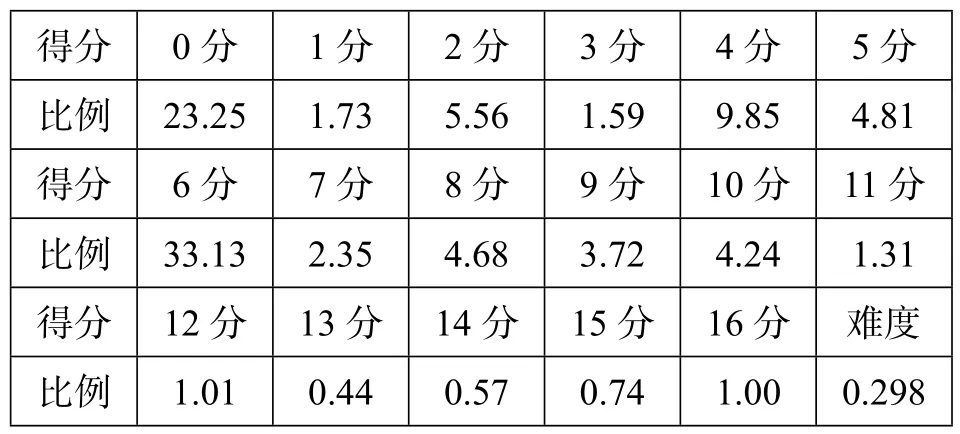
得分_ __0分_ __1分_ __2分_ __3分__ _4分_ __5分比例_ _23.25_ __1.73_ __5.56_ __1.59__ _9.85_ __4.81得分_ __6分_ __7分_ __8分_ __9分__ _10分_ _11分比例_ _33.13_ __2.35_ __4.68_ __3.72__ _4.24_ __1.31得分_ _12分_ _13分_ _14分_ _15分_ _16分_ _難度比例_ __1.01_ __0.44_ __0.57_ __0.74__ _1.00__ _0.298
在閱卷之余,筆者思考面對這樣的答題情況,教師該如何教學?由此,我對學生的答題情況進行了分析,對學生所犯的錯誤進行了歸納,并總結出教學啟示“基礎牢、審題清、用通法、‘分’點明、計算準、步驟精”,以期為我們的教學提供借鑒和幫助.(本題難度系數0.298)
二、試題回顧
(2015年江蘇省高考數學第19題,本小題滿分16分)已知函數f(x)=x3+ax2+b(a,b∈R)
(1)試討論f(x)的單調性;
(2)若b=c-a(實數c是與a無關的常數),當函數f(x)有三個不同的零點時,a的取值范圍恰好是,求c的值.
知識與能力要求 本題主要考查利用導數研究初等函數的單調性、極值及零點問題,第(2)問具有一定的新穎性與挑戰性,涉及逆向思維與“恰好成立”問題,考查綜合運用數學思想方法分析與解決問題以及代數推理能力.
命題思路及特色 本題以考生熟悉的三次函數為背景,使大多數考生都能入手,考查考生的數學素養和運算求解能力.本題反向提出問題,解決“恰好成立”問題,既要利用“兩邊夾”思想,先求出c的值,又要代入驗證,確保c的值滿足“恰好成立”.雖然題面表述簡潔,但是思維量較大.
解題思路 (1)利用導數在區間上的正負號,討論函數在相應區間上的單調性;(2)利用三次函數有三個零點時應具備的特性,結合三次函數有三個零點時a的取值范圍,確定c的取值范圍;(3)根據所得c的取值范圍,討論三次函數是否確實有三個零點,在保證恰好成立的前提下,最終得到所求c的值.



三、考生出現的錯誤及其分析
2.第一問考查單調性,單調區間不能用∪連接,f(x)單調遞增不交代區間不對(扣2分).但是結論下錯了,表格列對了不扣分.所以導數題最好列表;
4.因為評分標準是按步給分,一般一個得分點2分,多一個步驟得2分.因此考試過程中只要時間允許,一定要寫到沒得寫為止,比如一步2分共4分,不少考生認為后面不會做了,所以第二步2分沒得到;
5.求導不正確,導數求錯或f′(x)=0解出錯(常見錯誤答案) ,平時教學中,一定要重視概念、公式、定理的教學,基本知識是“三基”的根本;
6.審題要認真,準確完整地捕捉題目中的信息是解題的關鍵,平時教學過程中我們發現很多時候學生會把錯誤歸結到“看錯了”.如的解集為當作x的范圍,第一問有許多同學將單調性誤讀為奇偶性(有一人是0分+10分);
7.特殊到一般的思想方法,猜出答案的重要性,只要能得到答案c=1(得4分);
8.有些考生利用變量分離研究交點個數,由x3+ax2+ c -a = 0可知(解不出來).變量分離研究交點個數確實是比較有效的方法,前提是分離后的函數我們一定要能作圖,其實就是把一個復雜的圖變為兩個簡單的圖研究;
10.函數的零點式可以補充給學生(說清楚即滿分) ;
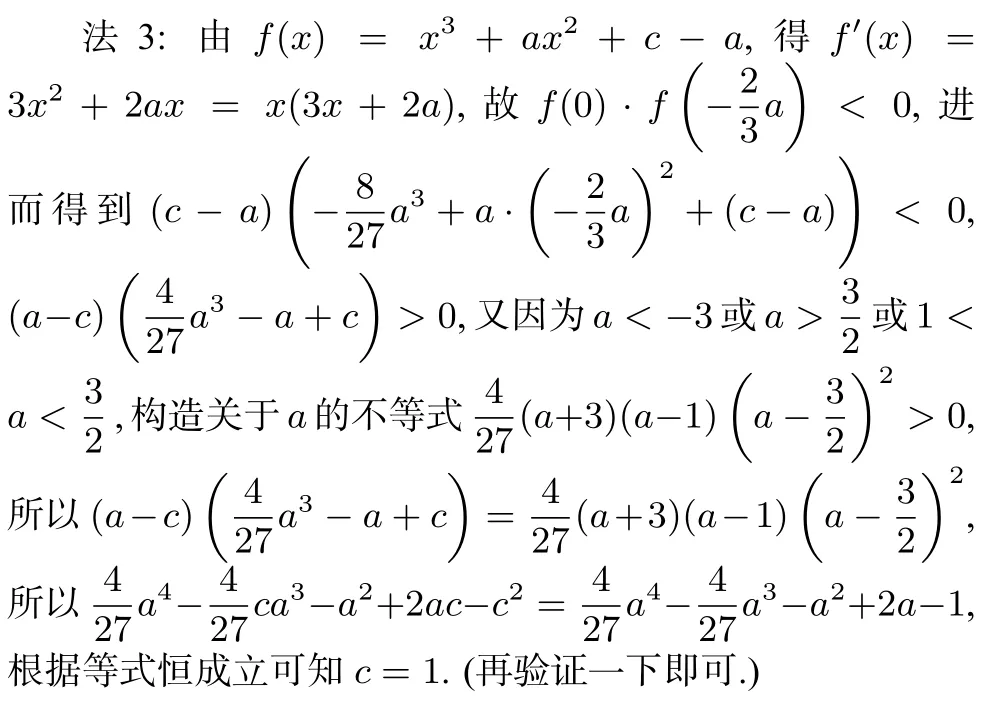
教學過程中有些內容課本進行了淡化或者刪除,但是為了知識的完整性和后續學習的需要,我們可以進行適當的補充.如三次函數的零點式、三垂線定理(分析問題)、數量積(投影)、橢圓的第三定義、阿波羅尼斯圓等.
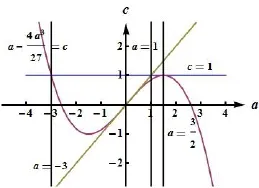
圖1
四、復習和教學建議
1.夯實基礎是永恒,突出主干知識是根本,理解記憶是保障
在高考卷中基礎題和中檔題所占比例最重,然而,通過閱卷發現很多學生在基礎知識的掌握和基礎能力的訓練方面非常薄弱,主干知識中的定理條件不清,公式記錯等錯誤比比皆是.所以在教學過程中要夯實基礎,突出主干知識落實,狠抓學生的記憶.教師要重視探究概念的形成過程,重視公式定理推導的過程.對重要的概念、公式反復強調,加深學生的記憶和理解.
2.通性通法是主流,淡化技巧是趨勢,規范答題是追求
從高考試題中可以明顯看出,高考重視對通性通法的考查.現在高考命題的一個原則就是淡化特殊技巧.因此指導學生復習中,不要刻意追求特殊解法,要更多地注重思考題目的“核心”是什么,屬于哪類題.閱卷過程中發現很多學生會做不會寫,在平時的教學中要幫助學生規范答題,明確題目的通性通法的得分點和解題步驟,要求學生按得分點、步驟書寫,嚴格訓練.
3.扎實提升“運算”和“推理”能力
就高考而言,可以說運算準確、合理、迅速是取得好成績的關鍵.面對數、代數式的基本運算,能敏銳察覺算式的結構特點,做到心算、估算、假算相結合;至于復雜的運算,則重在“算法”的設計,實際上“運算錯誤”不僅是技能不過關,更主要的是算法不好.教師要有意識地進行強化訓練的同時做到以下幾點:一是教師要充分發揮示范、引領、指導的作用,能詳細、規范書寫解題的推算過程,并對運算細節做必要的解釋與說明;二是對讓學生上臺板演,相互比較“算法”的優劣;三是杜絕計算器的使用;四是對于認為會做的題目而做錯了,要求學生通過自己獨立、耐心演算得到正確答案.
4.養成良好的解題教學習慣
認真審題是重要的好習慣,有的學生對審題重視不夠,匆匆一看急著下筆,無法吃透題目的條件和要求,無法從題目中挖掘隱含條件、啟發解題思路.學生的解題習慣很大程度上與教師的解題教學有關.有些教師在例題教學中,學生還沒有讀完題目就問“你有什么想法?”學生一時答不上來,老師就急著開始講,久而久之就影響了學生的解題習慣.教師要學會“等待”、“傾訴”,指導學生先寫出已知條件,用不同“語言”(文字語言、符號語言、圖形語言)表達條件,寫出需要求解的具體命題,理清解題思路并標注需要的條件等.

