動量定理在電磁感應題解中的應用

李元法

(湖北省當陽市第一高級中學，湖北 當陽 444100)

動量定理在電磁感應題解中的應用

李元法

(湖北省當陽市第一高級中學，湖北 當陽 444100)

2017年普通高考考試大綱修訂內容中,物理學科選修3-5列為必考內容,電磁感應現象在高考中出現的幾率將會進一步提升,動量定理和電磁感應現象聯系將更加緊密,探究動量定理在電磁感應現象中的應用將會顯示出更加重要的作用．

動量定理; 電磁感應現象; 應用模型

2014年9月,國務院頒布了《關于深化考試招生制度改革的實施意見》,2016年教育部考試中心修訂完善了考試大綱．目前,教育部考試中心對2017年普通高考考試大綱修訂內容進行了發布,其中物理學科將選修3-5的內容列為必考．不但使動力學知識更加完善,而且使動量部分和電磁感應現象相結合能進一步培養學生應用所學知識綜合分析問題、解決問題的能力．下面探究一下動量定理在電磁感應現象中的應用．

1 動量定理在電磁感應現象中和單桿相結合應用模型

1.1 單桿和電阻結合模型

單桿在磁場中切割磁感線是電磁感應現象中常見的模型,經常會出現做非勻變速運動類問題,當桿做非勻變速運動時不能直接用勻變速運動公式求解．應用動量定理和閉合電路歐姆定律、法拉第電磁感應定律相結合可以非常方便地求出桿運動的距離、速度、動能和瞬時功率．

圖1

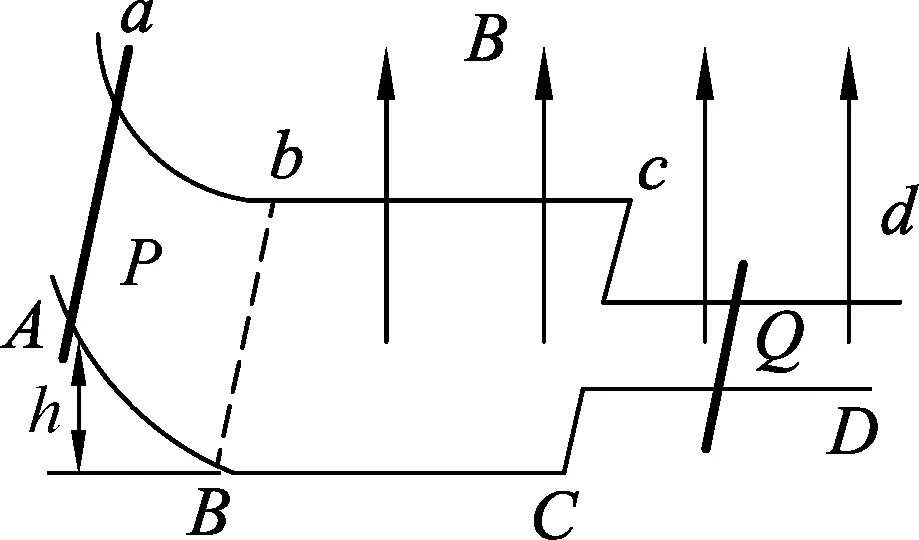
例1.如圖1所示,電阻不計、間距為L的光滑平行金屬導軌水平放置,導軌左側接有阻值為R的電阻,以導軌的左端為原點,沿導軌方向建立x軸,導軌處于豎直向下的磁感應強度大小為B的勻強磁場中,一根電阻也為R、質量為m的金屬桿垂直于導軌放置于x0處,不計金屬桿與導軌間的接觸電阻,現給金屬桿沿x軸正方向的初速度v0,金屬桿剛好能運動到2x0處,試求:金屬桿運動到1.5x0處時速度大小和安培力的瞬時功率．

解析:金屬桿受重力、支持力和水平向左的安培力;設金屬桿運動到1.5x0處時間為Δt,取水平向右為正．

由動量定理有

-BLΔt=mv-mv0.

(1)

由閉合電路歐姆定律有

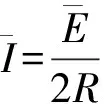
(2)

由法拉第電磁感應定律得

(3)

其中

ΔΦ=BLx02.

(4)

由(1)～(4)式得

-B2L2x04R=mv-mv0.

(5)

同理可得金屬桿運動到2x0處時有

B2L2x02R=mv0.

(6)

由(5)、(6)式得

v=v02.

當金屬桿運動到1.5x0處時,

E=BLv.

(7)

由閉合電路歐姆定律有

I=E2R.

(8)

金屬桿受到的安培力大小為

F=BIL.

(9)

由功率公式有

P=Fv.

(10)

由(7)～(10)式得P=B2L2v028R.

故金屬桿運動到1.5x0處時速度大小為v=v02，安培力的瞬時功率為P=B2L2v028R．

1.2 單桿和電容器結合模型

當單桿和電容器相結合時,桿運動切割磁感線產生感應電動勢,電容器會出現充、放電現象,電路中形成電流,桿受到安培力做變速運動最后達到穩定狀態做勻速運動,應用動量定理和電流的定義式、電容的定義式、法拉第電磁感應定律相結合可以簡潔明了地求出桿穩定運動的速度和電容器所帶電荷量．

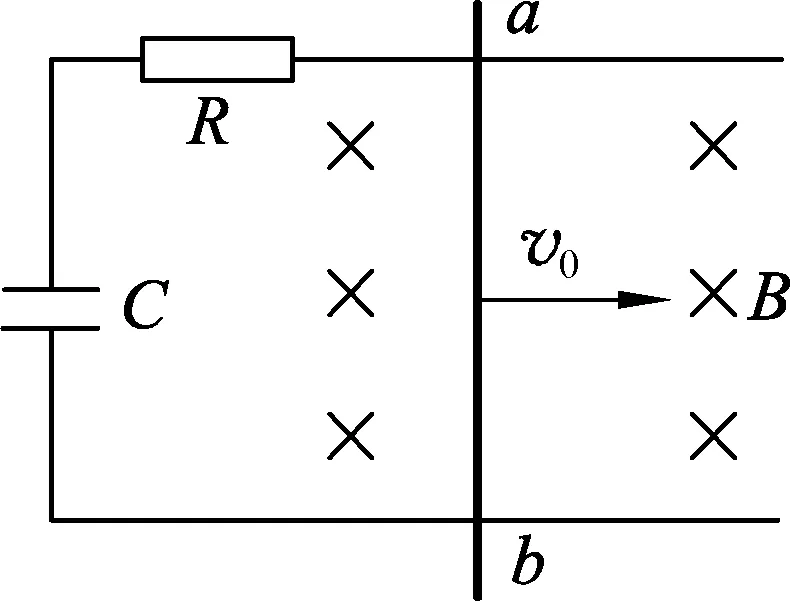
圖2

例2.在圖2中,除導體棒ab可動外,其余部分均固定不動,電容器C原來不帶電．設導體棒、導軌的電阻均可忽略,導體棒和導軌間的摩擦也不計,圖中裝置均在水平面內,且都處于方向垂直水平面(即紙面)向下的勻強磁場B中,導軌足夠長．導體棒的長度為L,質量為m,今給導體棒ab一個向右的初速度v0,試求:導體棒ab的最終運動速度．

解析:圖2中,導體棒向右運動切割磁感線產生感應電動勢使電容器充電,當電容器C極板間電壓與導體棒產生的感應電動勢相等時,電路中沒有電流,ab棒不再受安培力,向右做勻速運動.對導體棒:取水平向右為正，運動時間設為Δt.由動量定理有

(1)

由電流的定義式得

q=Δt.

(2)

由電容的定義式得

q=CU.

(3)

由法拉第電磁感應定律得

U=BLv.

(4)

由(1)～(4)式得

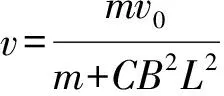
2 動量定理在電磁感應現象中和線圈相結合應用模型

線圈模型是物理學中常見模型,線圈進入和離開磁場時切割磁感線產生感應電動勢,線圈本身組成閉合回路形成電流,線圈受到安培力．應用動量定理和動能定理、法拉第電磁感應定律巧妙結合可以準確求出線圈運動時間、速度和動能．下面為線圈在磁場中運動的兩種模型．

2.1 線圈在水平面上運動模型

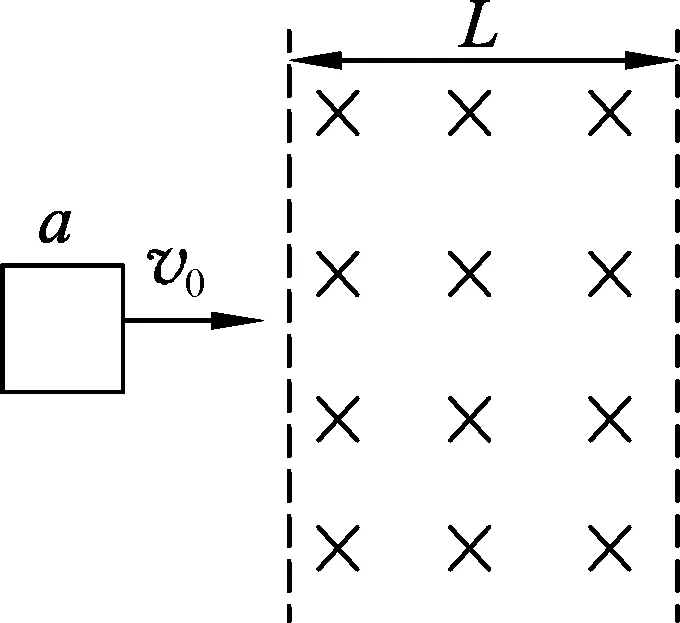
圖3 物理情景示意圖

例3.如圖3所示,在光滑的水平面上,有一豎直向下的勻強磁場分布在寬度為L的區域內,現有一個邊長為a(a

解析:線圈受重力、支持力和水平向左的安培力;設線圈質量為m,完全進入磁場中時運動時間為Δt,線圈的速度為v1、線圈的電阻為R,取水平向右為正．由動量定理有

-BaΔt=mv1-mv0.

(1)

由閉合電路歐姆定律得

(2)

由法拉第電磁感應定律有

(3)

其中

ΔΦ=Ba2.

(4)

由(1)～(4)式得

-B2a3R=mv1-mv0.

(5)

同理可得線圈完全離開磁場時有

-B2a3R=mv-mv1.

(6)

由(5)、(6)式得線圈完全進入磁場中時線圈的速度為

2.2 線圈在豎直方向上運動模型

圖4

例4.如圖4所示,a、b是邊界范圍、磁感應強度大小和方向都相同的兩個勻強磁場區域,a的下端離水平地面的高度比b高一些．甲、乙是兩個完全相同的閉合正方形導線框,分別位于a、b的正上方,兩線框的下端離地面的高度相同．兩線框由靜止同時釋放,穿過磁場后落到地面,下落過程中線框平面始終保持與磁場方向垂直．試比較甲、乙兩線框落地時間．

解析:設線框的邊長為L，線框離地高度為h,質量為m，電阻為R,線框運動時間為t，穿入和穿出的時間為Δt、落地速度設為v．

對線框:受重力,穿入和穿出磁場時受向上安培力,取向下為正方向．由動量定理有

mgt-BLΔt=mv.

(1)

由閉合電路歐姆定律有

(2)

由法拉第電磁感應定律有

(3)

其中

ΔΦ=2Bl2.

(4)

由(1)～(4)式得

t=mvR+2B2L3mgR.

(5)

乙進入磁場時速度較大,安培力較大,克服安培力做功多,乙線框中產生的熱量較多．

由動能定理有

(6)

由(1)～(6)式得t甲>t乙故乙線框先落地.

3 動量定理在電磁感應現象中和雙桿相結合應用模型

在雙桿模型中,一般情況下兩桿是變速運動,兩桿受到的安培力是變力,學生在解答中有一定的難度,近幾年在高考中較少命題． 但應用動量定理可以巧妙地解決電磁感應現象中的變力和變速問題．下面為雙桿運動的兩種模型．

3.1 雙桿長度不相等類模型

圖5

例5.如圖5所示,光滑平行異形導軌ABCD與abcd,導軌的水平部分BCD處于豎直向上的勻強磁場中,BC段導軌寬度為CD段軌道寬度2倍,軌道足夠長.將質量相同的金屬棒P和Q分別置于軌道上的AB和CD段,將P棒由水平軌道高為h的地方由靜止釋放,使其自由下滑,求:P棒和Q棒的最終速度．

解析:設P、Q棒的質量為m,長度分別為2L和L,磁感應強度為B,P棒進入水平軌道的速度為v．

對金屬棒P:下落h過程由動能定理有

mgh=12mv2.

(1)

則棒剛進入磁場時的速度為

v=2gh.

(2)

當P棒進入水平軌道后,切割磁感線產生感應電流.P棒受到安培力作用而減速,Q棒受到安培力作用而加速,Q棒運動后也將產生感應電動勢,與P棒感應電動勢反向,因此回路中的電流將減小.最終達到勻速運動時,回路的電流為零．即

2BLvP=BLvQ.

(3)

設P棒從進入水平軌道開始到速度穩定所用的時間為Δt,I為回路中的電流，取水平向右的方向為正方向．

對金屬棒P:由動量定理得

-2BILΔt=mvP-mv.

(4)

對金屬棒Q:由動量定理得

BILΔt=mvQ-0.

(5)

由(2)～(5)式得P棒和Q棒的最終速度分別為

vP=152gh，vQ=252gh.

2.2 雙桿長度相等類模型

圖6

例6.(2003年全國理綜天津卷)如圖6所示,兩根平行的金屬導軌,固定在同一水平面上,磁感應強度B=0.50 T的勻強磁場與導軌所在平面垂直,導軌的電阻很小,可忽略不計．導軌間的距離l=0.20 m．兩根質量均為m=0.10 kg的平行金屬桿甲、乙可在導軌上無摩擦地滑動,滑動過程中與導軌保持垂直,每根金屬桿的電阻為R=0.5 Ω．在t=0時刻,兩桿都處于靜止狀態．現有一與導軌平行、大小為0.20 N的恒力F作用于金屬桿甲上,使金屬桿在導軌上滑動．經過t=5.0 s,金屬桿甲的加速度為a=1.37 m/s2,問此時兩金屬桿的速度各為多少?

解析:設任一時刻t兩金屬桿甲、乙之間的距離為x,速度分別為v1和v2,經過很短的時間Δt,甲桿移動距離v1Δt,桿乙移動距離v2Δt,回路面積改變為

ΔS=[(x-v2Δt)+v1Δt]l-lx=

(v1-v2)lΔt.

(1)

由法拉第電磁感應定律,回路中的感應電動勢為

E=BΔSΔt.

(2)

回路中的電流為

i=E2R.

(3)

甲桿的運動方程為

F-Bli=ma.

(4)

由于作用于甲桿和乙桿的安培力總是大小相等,方向相反．對甲、乙兩桿:由動量定理得

Ft=mv1+mv2.

(5)

由(1)～(5)式解得

v1=12F1m+2RB2F(F-ma),

v2=12F1m-2RB2I2(F-ma).

代入數據得v1=8.15 m/s,v2=1.85 m/s.

綜上所述,在電磁感應現象中應用動量定理解題,使解題過程更加簡潔、清晰明了，既能培養學生綜合分析問題、解決問題的能力,又能滿足高校選拔優秀人才要求．

1 姜鋼.探索構建高考評價體系，全方位推進高考內容改革[N]．中國教育報，2016(10)．

2016-11-28)