區間值信息系統的多粒度粗糙集及其決策

郭 慶, 戴習民

(1.合肥工業大學 數學學院,安徽 合肥 230009; 2.合肥工業大學 管理學院,安徽 合肥 230009)

區間值信息系統的多粒度粗糙集及其決策

郭 慶1,2, 戴習民1

(1.合肥工業大學 數學學院,安徽 合肥 230009; 2.合肥工業大學 管理學院,安徽 合肥 230009)

文章從多粒度視角研究了區間值信息系統(interval-valued information system，IvIS)，定義了多粒度容差關系,給出了樂觀和悲觀的2種模型,研究了其性質及其與單粒度模型的聯系與區別;然后定義了區間值決策系統(interval-valued decision system，IvDS)的多粒度決策規則的置信度因子及決策規則提取方法,并且給出了決策規則支持定理及其證明;最后通過一個算例驗證了所提理論方法的正確性與有效性。

多粒度;粗糙集;區間值信息系統(IvIS);決策規則;置信度因子

粗糙集理論經過了30多年的研究與發展,已在理論和應用中取得了長足的進展,被廣泛應用于數據挖掘、知識獲取等領域中[1-2]。但從粒計算角度來說,現有的模型都是建立在單粒度基礎上的,稱之為單粒度粗糙集。這種單個等價關系從某種程度上限制了對數據的處理。為此,文獻[3]在此基礎上將單粒度粗糙集模型拓展到多粒度情形。近幾年來多粒度粗糙集吸引了大量的研究學者,例如文獻[4]研究了悲觀多粒度粗糙集的決策問題；文獻[5]于模糊近似空間建立了模糊粗糙集的多粒度模型并加以應用；文獻[6]建立了鄰域信息系統的1-型和2-型多粒度粗糙集模型。

在許多現實問題中,信息系統中的數據由于噪聲、獲取缺損的信息等因素,導致許多數據不再是確定的值,而屬于某一范圍即以區間值形式存在。例如政府信息公開中,各種指標的評價值往往只是一個范圍,高校學生對教師教學水平各項指標的評價值也是一個范圍等。這種形式的數據表稱為區間值信息系統(interval-valued information system，IvIS)[7]。近年來,IvIS的屬性約簡理論得到了大量的研究與應用,詳細內容可參考文獻[8-10]。

但是現有的多粒度粗糙集模型涉及到IvIS的研究甚少。本文針對此問題引入多粒度容差關系,構建IvIS的樂觀多粒度粗糙集模型和悲觀多粒度粗糙集模型,對它們的基本性質和單粒度模型之間的區別及其聯系進行討論,從多粒度視角給出了區間值決策系統的規則提取方法與規則的置信度因子。

1 預備知識

1.1 區間值信息系統(IvIS)

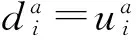
定義2[8]設T=(U,A)是一個IvIS,a∈A,λ∈[0,1]。定義T上關于a的λ-容差關系如下:

其中，|·|表示集合的基數。關于區間數的交與并運算可參考文獻[7]。樣本x關于a的λ-容差類定義為：

1.2 多粒度粗糙集

在多粒度粗糙集中,一個目標概念是用一族等價關系而非單個等價關系來近似的,根據近似的要求不同,通常分為樂觀多粒度粗糙集與悲觀多粒度粗糙集2種模型。

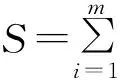
其中,[x]Ai={y:(x,y)∈RAi}是由所有與樣本x基于屬性集合Ai導出的等價類組成的集合。

定義4 設T=(U,A)表示一個信息系統,Ai?A(i=1,2,…,m)表示m個屬性子集,對任意的X?U,關于Ai的悲觀多粒度下、上近似集分別定義為:

2 IvIS的多粒度粗糙集及其性質

2.1IvIS的多粒度粗糙集模型

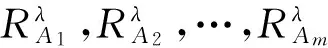
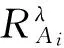
定義6 設T=(U,A)是一個IvIS,Ai?A(i=1,2,…,m)表示m個屬性子集,λ∈[0,1]。對任意的目標集合X?U,上述容差關系下的樂觀多粒度下近似集、上近似集及邊界集定義為：

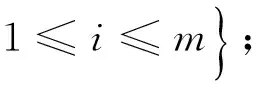
定義7 設T=(U,A)是一個IvIS,Ai?A(i=1,2,…,m)表示m個屬性子集,λ∈[0,1]。對任意的目標集合X?U,上述容差關系下的悲觀多粒度下近似集、上近似集及邊界集定義為:

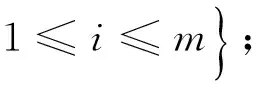
2.2 模型相關性質

由定義6與定義7可得下列性質。

性質1 設T=(U,A)是一個IvIS,Ai?A(i=1,2,…,m)表示m個屬性子集,λ∈[0,1],X,Y?U,則

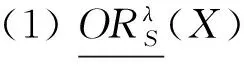
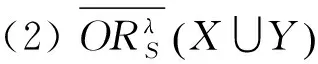
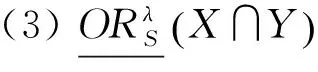
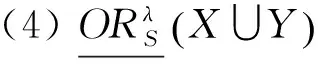
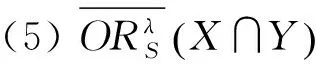
證明 此處只證明樂觀的情況,悲觀的情況類似。

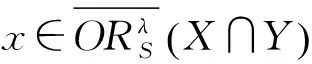
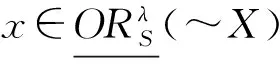
性質2 設T=(U,A)是一個IvIS,Ai?A(i=1,2,…,m)表示m個屬性子集,λ∈[0,1],X?U,則

證明 只證明每個性質的前半部分,后半部分證明類似。

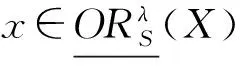
(2) 證明與(1)類似,從略。

性質2揭示了目標集合在單個粒度與多個粒度下的上下近似之間的等價關系。

3 決策規則

從決策表中導出決策規則是粗糙集理論最重要的應用之一,區間值決策系統(interval-valued decision system，IvDS)中的決策規則可由下近似集中的對象所支持,所得到的決策規則是確定型規則;而可能型規則由邊界域中對象所支持。本節給出多粒度背景下IvDS決策規則的前件的邏輯連接詞是“或”而非“且”的決策規則。

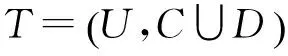
其中,[x]d表示在決策屬性d下與x同一等級的對象。

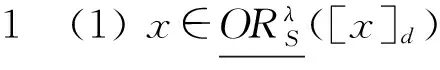
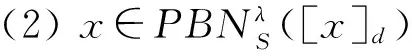
(2) 證明與(1)的證明類似。

定理1表明在IvDS中的確定性“或”規則可由樂觀多粒度下近似集中的對象支持;可能性“或”規則可由悲觀多粒度邊界集中的對象支持。

4 算例分析

基于多個專家評估的決策系統見表1所列,其中xi表示學生；ai表示第i個專家基于本領域的知識給出的評價值。考慮到評估的不確定性,

這里都用區間值來表示,設Ai={ai},d表示學生綜合分值,U/D={D1,D2,D3}={(x4),(x1,x3),(x2,x5,x6)}。

取容差水平λ=0.2,由定義2、定義6和定義7可計算出:

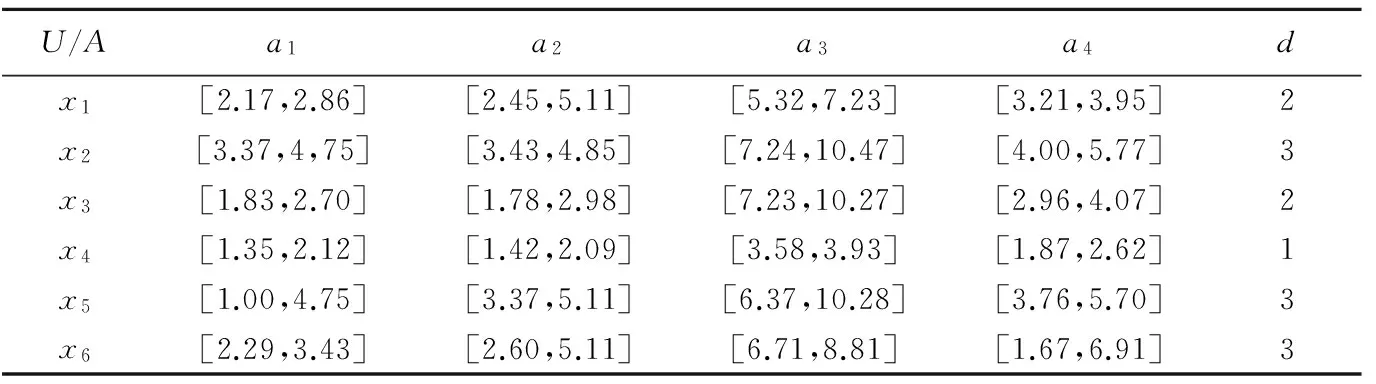
表1 專家評估決策系統

由定理1可得該決策系統的確定性“或”決策規則如下:

f(x,a1)∩[1.35,2.12]>0.2∨f(x,a2)∩[1.42,2.09]>0.2∨f(x,a3)∩[3.58,3.93]>0.2∨f(x,a4)∩[1.87,2.62]>0.2→d(x)=1,由樣本x4支持。

f(x,a1)∩[2.17,2.86]>0.2∨f(x,a2)∩[2.45,5.11]>0.2∨f(x,a3)∩[5.32,7.23]>0.2∨f(x,a4)∩[3.21,3.95]>0.2→d(x)=2,由樣本x1支持。

f(x,a1)∩[1.83,2.70]>0.2∨f(x,a2)∩[1.78,2.98]>0.2∨f(x,a3)∩[7.23,10.27]>0.2∨f(x,a4)∩[2.96,4.07]>0.2→d(x)=2,由樣本x3支持。

f(x,a1)∩[3.37,4.75]>0.2∨f(x,a2)∩[3.43,4.85]>0.2∨f(x,a3)∩[7.24,10.47]>0.2∨f(x,a4)∩[4.00,5.77]>0.2→d(x)=3,由樣本x2支持。

f(x,a1)∩[1.00,4.75]>0.2∨f(x,a2)∩[3.37,5.11]>0.2∨f(x,a3)∩[6.37,10.28]>0.2∨f(x,a4)∩[3.76,5.70]>0.2→d(x)=3,由樣本x5支持。

上述結果表明,多粒度模型能夠從決策系統中導出更為寬松的決策規則,從而使實際決策更合理。

5 結 論

本文研究了IvIS的多粒度粗糙集理論,定義了樂觀和悲觀2種模型,研究了其性質以及與單粒度模型之間的關系,并且給出了多粒度IvDS決策規則的置信度因子及其決策規則的獲取方法,最后通過實例加以驗證。作為粗糙集理論的一個較新的研究方向,多粒度粗糙集為決策問題提供了新的思路與方法,下一步研究工作的重點是在多準則決策分析方面的應用。

[1] PAWLAK Z.Rough set theory and its applications to data analysis[J].Cybernetics and Systems,1998,29(7):661-688.

[2] 張勇,張麗,劉心報,等.基于限制優勢關系粗糙集的高校學生心理危機預警要素分析[J].合肥工業大學學報(自然科學版),2013,36(12):1523-1527.

[3] QIAN Y H,LIANG J Y,YAO Y Y.MGRS:A multi-granulation rough set[J].Information Sciences,2010,180(6):949-970.

[4] QIAN Y H,SANG Y L,LIANG J Y.Pessimistic rough set based decisions:a multi-granulation fusion strategy[J].Information Sciences,2014,264(2):196-210.

[5] XU W H,WANG Q R.Multi-granulation fuzzy rough sets in a fuzzy tolerance approximation space[J].International Journal of Fuzzy Systems,2011,13(4):246-259.

[6] LIN G P,QIAN Y H,LI J J.NMGRS:Neighborhood-based multigranulation rough sets[J].International Journal of Approximate Reasoning,2012,53(7):1080-1093.

[7] 郭慶,劉文軍,焦賢發.一種基于模糊聚類的區間值屬性約簡算法[J].模糊系統與數學,2013,27(1):149-153.

[8] LEUNG Y,MANFRED M F.A rough set approach for the discovery of classification rules in interval-valued information systems[J].International Journal of Approximate Reasoning,2008,47(2):233-246.

[9] DU W S,HU B Q.Approximate distribution reducts in inconsistent interval-valued ordered decision tables[J].Information Sciences,2014,271(1):93-114.

[10] ZHANG H Y,LEUNG Y,ZHOU L.Variable-precision dominance based rough set approach to interval-valued information systems [J].Information Sciences,2013,244(1):75-91.

(責任編輯 朱曉臨)

Multi-granulation rough set and decision in interval-valued information system

GUO Qing1,2, DAI Ximin1

(1.School of Mathematics, Hefei University of Technology, Hefei 230009, China; 2.School of Management, Hefei University of Technology, Hefei 230009, China)

Interval-valued information system(IvIS) is investigated from the perspective of multi-granulation. The optimistic model and pessimistic model are proposed by multi-tolerance relation. Then their properties are researched and the differences and relationships compared with single-granulation model are discussed. Moreover, the certainty factor of the decision rule as well as acquisition method of interval-valued decision system(IvDS) is given. The decision rules support theorem is proposed and proved. Finally, a numerical example is given to demonstrate the correctness and effectiveness of the proposed method.

multi-granulation; rough set; interval-valued information system(IvIS); decision rule; certainty factor

2015-08-17；

2015-11-23

國家自然科學基金資助項目(71131002);中央高校基本科研業務費專項基金資助項目(2015HGZX0019);安徽省省級質量工程專業綜合改革試點資助項目(2012zy007)和名師(大師)工作室資助項目(2015msgzs126)

郭 慶(1979-),男,安徽霍邱人,合肥工業大學講師.

10.3969/j.issn.1003-5060.2017.02.027

O159

A

1003-5060(2017)02-0284-05