計及熱傳導影響對長桿彈侵徹陶瓷靶的數值分析*

李芮宇,孫宇新,周 玲,孫其然,趙亞運,馮江拓

(1.南京理工大學瞬態物理重點實驗室,江蘇南京210094; 2.中國兵器科學研究院,北京100000)

計及熱傳導影響對長桿彈侵徹陶瓷靶的數值分析*

李芮宇1,孫宇新1,周 玲2,孫其然1,趙亞運1,馮江拓1

(1.南京理工大學瞬態物理重點實驗室,江蘇南京210094; 2.中國兵器科學研究院,北京100000)

采用有限元方法離散瞬態熱傳導方程,編寫成侵徹過程熱傳導計算模塊,并將之嵌入已有的沖擊動力學程序中,然后運用于長桿彈在900～1 800 m/s著速范圍內侵徹AD95陶瓷靶的數值分析,得到了符合物理事實的計算圖像,所得的計算結果比采用傳統的絕熱模型得到的計算結果更符合實驗結果。探討了計及熱傳導效應對長桿彈侵徹AD95陶瓷靶數值模擬的影響:著速在900～1 350 m/s范圍內時,計及熱傳導的數值計算所得侵深小于絕熱模型計算結果;著速在在1 350～1 450 m/s范圍內時,兩種模型計算侵深接近;著速在在1 450～1 800 m/s范圍內時,熱傳導模型計算侵深大于絕熱模型計算結果。

侵徹;熱傳導;有限元;陶瓷

長桿彈侵徹過程中,彈靶界面塑性變形嚴重,產生大量的熱,引起材料溫升,進而導致材料的力學性能發生改變。所以,侵徹計算時必須考慮溫度因素。對此,李永池等[1]對鎢合金熱塑性互動損傷和平頭彈丸沖塞進行了計算,考慮了溫度對材料參數和損傷演化的影響;晏麓暉等[2]研究了絕熱軟化對空腔膨脹數值模擬的影響,發現不計入熱效應會高估侵徹阻力;趙攀峰等[3]將溫度軟化考慮進數值計算中,研究了桿彈高速貫穿金屬靶的有關規律。材料出現局部溫升必然存在熱傳導現象,影響材料的溫度分布和力學行為。然而,既往的數值計算[4-6]中普遍忽略了熱傳導因素,計算結果必然與真實狀況存在差異。

本文中,將熱傳導模塊嵌入沖擊動力學源代碼,運用于長桿彈侵徹AD95陶瓷靶的數值分析,并將得到的計算結果與絕熱模型計算結果進行比較。

1 計算物理模型

IMPACT-2D是基于連續介質力學的Lagrange型基本守恒方程所編寫的源代碼,主要用于高速撞擊現象的數值分析和數值模擬計算,是在借鑒其他有限元軟件的基礎上開發完成的。但是在軟件開發初期未考慮沖擊過程中的熱傳導,無法分析熱傳導對沖擊問題模擬的影響,所以有必要引入熱傳導方程。軸對稱導熱微分方程為:

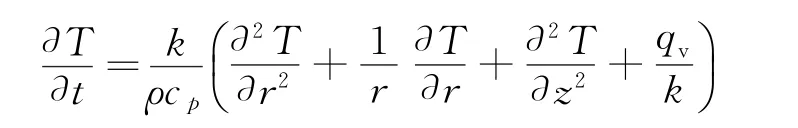
式中:T為物體的瞬態溫度,t為時間,k為材料的導熱系數,ρ為材料密度,cp為材料的比熱,qv為材料的內熱源強度。

由于有限元熱傳導計算是基于節點的,而有限元沖擊計算的溫度儲存在單元中,程序在計算單元應力時采用的也是單元的溫度,只是在后處理時將單元的溫度轉換在節點上。但是無法通過該轉換方法將節點的溫度再轉換回單元,所以在進行熱傳導計算時必須建立一個背景網格,方法是:以單元的中心節點為熱傳導計算的節點,以此構建背景網格。每一個循環結束后,以單元的溫度為初始條件作為背景網格節點的溫度,進入熱傳導模塊進行計算,這樣就實現了單元溫度的更新,并以更新后的單元溫度進行下一步循環計算。如此一來,程序就實現了沖擊過程中的熱傳導計算。圖1為背景網格示意圖:i～l為原始三角形單元,1～6為原始三角形單元節點,用于計算侵徹過程中材料的應力應變等;a～d為背景網格節點,用于原始單元之間的熱傳導計算。

2 模型及參數

針對孫宇新等[7]的長桿彈侵徹陶瓷復合靶的實驗進行數值模擬,彈丸材料為35Cr MnSi,口徑為7.62 mm,長約70 mm。復合靶由蓋板/陶瓷靶/鑒證靶組成,靶板直徑為96 mm。蓋板的材質為A3鋼,厚度為2 mm;陶瓷靶材質為AD95陶瓷,直徑為80 mm,總厚度為30 mm;鑒證靶材質也采用A3鋼。在陶瓷靶外緊圍一圈由45鋼制成的套筒以實現對陶瓷的徑向約束,壁厚8 mm。建立二維軸對稱離散模型,如圖2所示,三角形單元總數為36 000。

采用線性溫升軟化關系[8]計算溫度對彈性模量、泊松比等物理量的影響,采用Johnson-Cook本構模型描述溫度對金屬材料屈服應力的影響,并采用Grüneisen狀態方程。35Cr MnSi[9]、A3鋼[10]和45鋼[11]的材料參數如表1所示。對AD95陶瓷材料采用JH-2模型[12]描述,參數[13]分別為:ρ0= 3.625 g/cm3,A=0.88,N=0.64,C=0.007,σt=0.262 GPa,B=0.28,M=0.60,σHEL=5.3 GPa,σHEL,eff=3.75 GPa,pHEL=2.8 GPa,G=109.7 GPa,K1=228.6 GPa,K2=191.4 GPa,K3=111.5 GPa,

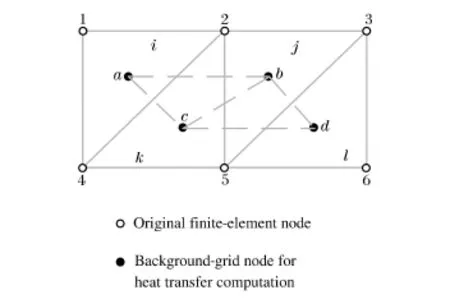
圖1 溫度背景網格示意圖Fig.1 Diagram of temperature background grid

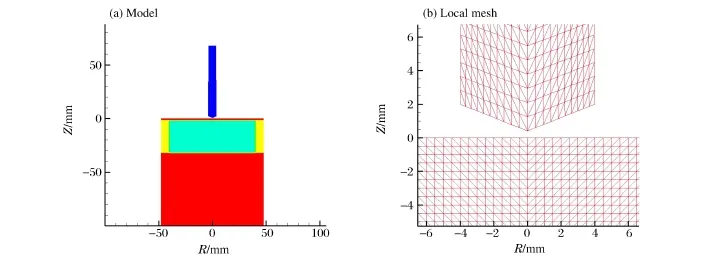
圖2 模型及局部網格Fig.2 Model and local mesh

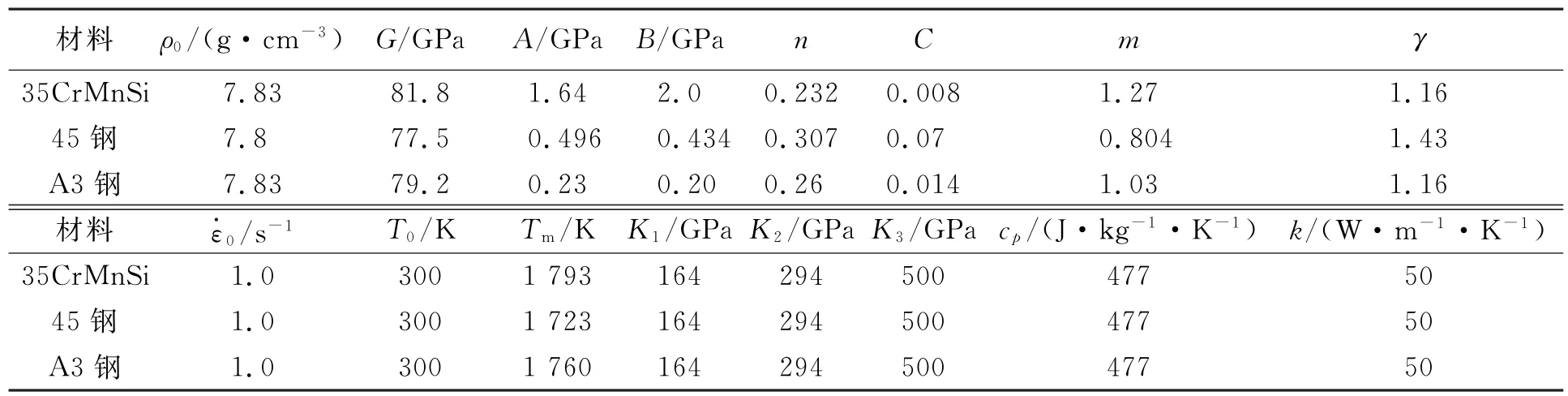
表1 3種金屬的材料參數Table 1 Parameters of three metals

3 計算結果及分析

3.1 結果驗證

圖3給出了考慮熱傳導時,著速為1 054 m/s的長桿彈對陶瓷復合靶的侵徹過程。彈體的銷蝕、蓋板的鼓起、陶瓷靶正面的開坑、陶瓷靶內部裂紋的擴展等現象在圖3中均得到了清晰的描述,與圖4實驗現象十分吻合,這也表明本文中所用程序及選取的材料模型及參數是可靠的。

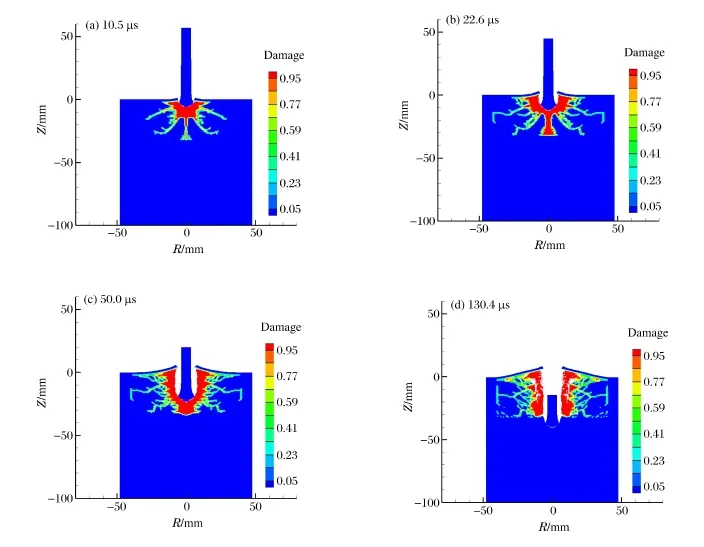
圖3 典型長桿彈侵徹陶瓷靶過程中的損傷云圖(1 054 m/s)Fig.3 Damage distribution of the ceramic target penetrated by a typical long-rod projectile of 1 054 m/s

圖4 典型長桿彈侵徹后的AD95陶瓷靶(1 054 m/s)Fig.4 AD95 ceramic target penetrated by a typical long-rod projectile of 1 054 m/s

3.2 模擬結果分析

3.2.1 侵深與著速的關系

圖5給出了分別采用絕熱模型和熱傳導模型計算得到的長桿彈侵深D隨著速v0的變化關系(圖5 (a))以及兩種模型計算侵深的差值百分比隨彈體著速的變化關系(圖5(b)),其中D1為熱傳導模型計算侵深,D2為絕熱模型計算侵深。由圖5(b)可以看出兩種模型計算侵深的差值百分比最大可達3%,因此熱傳導因素對長桿彈侵深有較顯著的影響,當彈體著速在900～1 350、1 350～1 450和1 450～1 800 m/s等3個范圍內時,熱傳導模型計算侵深分別小于、接近、大于絕熱模型計算結果。由圖5(a)可以看出熱傳導模型計算結果同實驗結果最接近,這說明在侵徹計算中對彈體考慮熱傳導效應很有必要。下面將從侵徹過程中長桿彈的面密度變化、壓力變化等方面來解釋圖5呈現的現象。

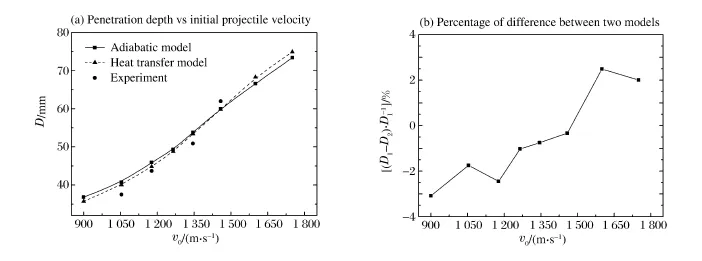
圖5 兩種模型計算侵深的比較Fig.5 Comparison between the two models on penetration depth

3.2.2 彈體侵徹過程中的面密度和侵深

在此取2個典型著速(900和1 750 m/s)來說明問題,這2個著速分別代表圖5中的2種情況:熱傳導模型計算侵深低于和高于絕熱模型計算侵深。圖6(a)、(b)分別為900和1 750 m/s著速下的彈體面密度ρa和侵深時程曲線。由圖6可以發現對應的2種侵徹過程:(1)彈體著速為900 m/s時,在約40μs后熱傳導模型對應的彈體面密度開始顯著小于絕熱模型對應的彈體面密度,以致其侵徹過程所承受的平均過載較大,最終使得侵深低于后者;(2)彈體著速為1 750 m/s時,總體上,熱傳導模型對應的彈體面密度高于絕熱模型對應的彈體面密度,其平均過載也就低于后者,侵深比絕熱模型計算結果大。

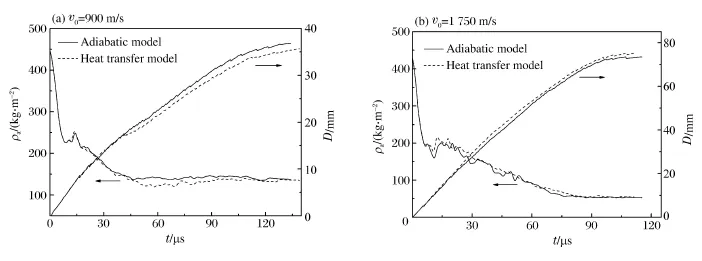
圖6 彈體面密度和侵深時程曲線Fig.6 Areal density-and penetration depth-time curves of the long-rod projectile at different initial penetration velocities

3.2.3 侵徹過程中的彈頭壓力變化

圖7給出了2種典型著速下侵徹過程中彈頭的壓力時程曲線,在900和1 750 m/s的著速下,彈體侵徹過程所受的最大壓力分別為10和22 GPa,遠高于彈體材料的靜態屈服強度Y0(1.64 GPa)。圖8為侵徹過程中彈頭平均壓力p隨彈體著速的變化關系,可見隨彈體著速v0的升高,彈頭在侵徹過程中所受平均壓力也隨之升高,可將本文中長桿彈侵徹陶瓷復合靶的過程分為3個階段,見表2。

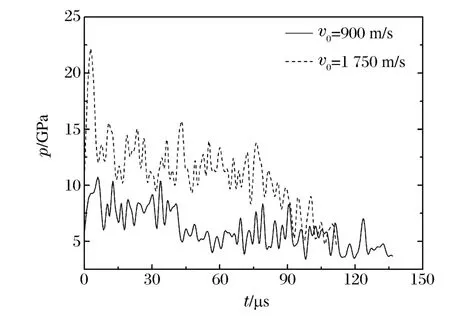
圖7 侵徹過程中彈頭的壓力時程曲線Fig.7 Pressure-time curves of the projectile head during penetration

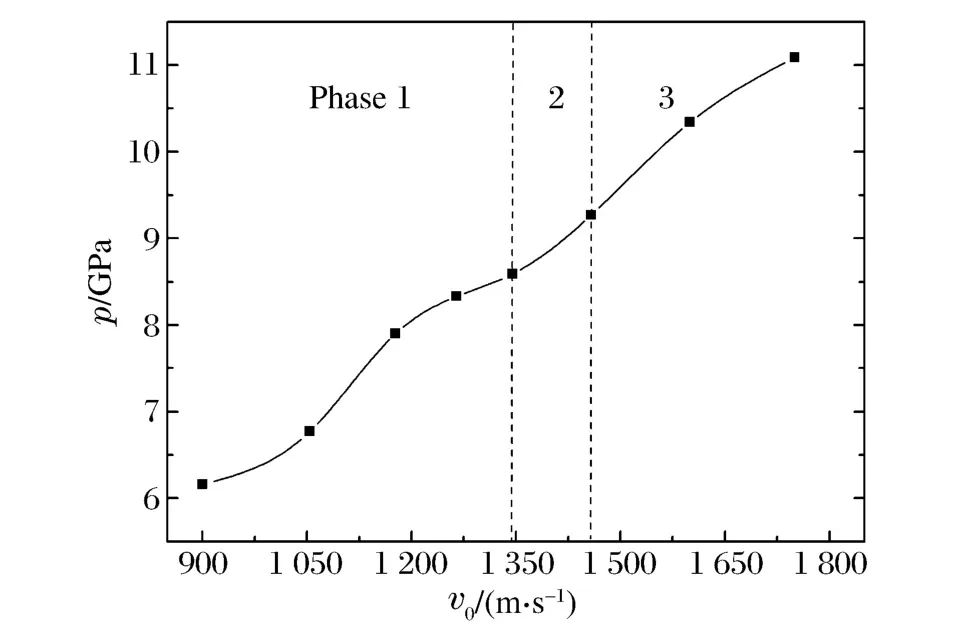
圖8 侵徹過程中彈頭平均壓力隨著速的變化Fig.8 Average pressure of the projectile head varied with initial penetraion velocity during penetration

表2 長桿彈侵徹陶瓷復合靶3個階段Table 2 Three phases of long-rod projectiles penetration into ceramic composite targets

3.2.4 原因分析

由3.2.1～3.2.3節的分析可知,熱傳導對長桿彈侵徹計算有較顯著的影響,且存在如圖5和表2所示的規律。圖9為900和1 750 m/s的著速下長桿彈侵徹過程中的剩余質量變化,可見在著速為900 m/s時熱傳導模型對應的剩余質量一直小于絕熱模型對應的剩余質量;著速1 750 m/s時,熱傳導模型對應的剩余質量一直大于絕熱模型對應的剩余質量,90μs后熱傳導模型對應的剩余質量開始向后者靠攏。由以上可以認為:當著速較低時(小于1 350 m/s),考慮熱傳導因素會使彈體在侵徹過程中銷蝕更快;當著速較高時(大于1 450 m/s),考慮熱傳導因素會使彈體在侵徹過程中銷蝕變慢。

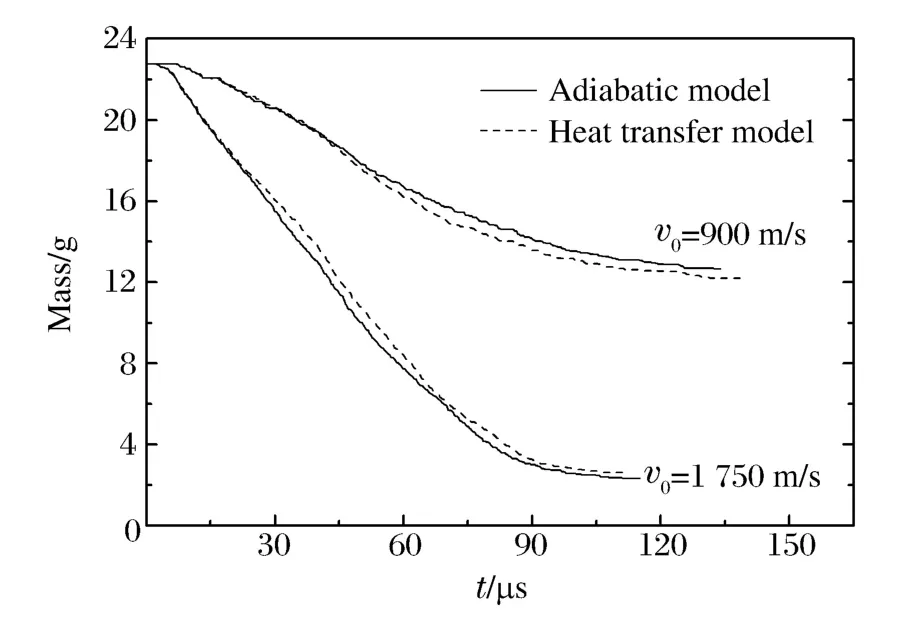
圖9 兩種模型長桿彈剩余質量時程曲線Fig.9 Residual mass-time curves by two models

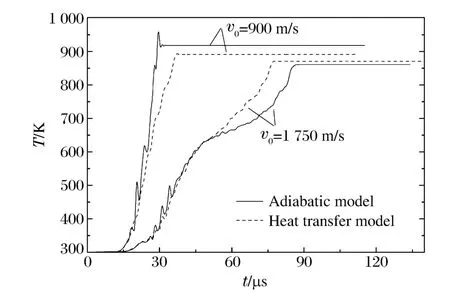
圖10 觀測點溫度時程Fig.10 Temperature-time curves of observation points

有限元計算中,單元的銷蝕與塑性應變相關,塑性應變達到閾值時,會被刪除。考慮熱效應時,單元的應變與溫度有很大的關系,單元溫度升高,材料的剪切模量和屈服應力會下降,單元抵抗變形的能力也隨之降低,其應變就會越早達到閾值,被刪除。圖10給出了彈體軸線距彈頭20 mm處單元的溫度時程曲線,可見:900 m/s時熱傳導模型觀測點溫度增長速度快于絕熱模型,較早于后者達到銷蝕應變,被刪除;1 750 m/s時結果與900 m/s時正好相反。這是因為低速時彈頭壓力低(圖8),單元應變率低,應變達到銷蝕值所經歷的時間長,彈頭由于塑性變形產生的高熱量有著較長的時間向后擴散,以致傳入后方單元的熱量多于后方單元傳出的熱量,使得該單元含有的熱量高于絕熱模型,高速情況下與之相反。

4 結 論

將熱傳導因素引入沖擊動力學程序,對典型長桿彈侵徹陶瓷靶的過程進行數值計算,將計算結果與采用絕熱模型得到的計算結果進行比較,發現長桿彈著速由低到高變化時,熱傳導對侵深的影響不同:長桿彈著速為900～1 350 m/s時,由于熱傳導模型彈銷蝕速度較快,其計算侵深小于絕熱模型計算結果;長桿彈著速為1 350～1 450 m/s時,兩種模型彈銷蝕速度接近,所以計算侵深接近;長桿彈著速為1 450～1 800 m/s時,熱傳導模型彈銷蝕速度慢于絕熱模型,其計算侵深大于后者計算侵深。由數據對比發現熱傳導模型計算侵深隨著速的變化規律與實驗數據更接近,這說明侵徹過程中考慮熱傳導因素所得結果更合理可信。本研究改善了傳統侵徹計算中忽略熱傳導的狀況,可為相關研究提供參考。

[1] 李永池,袁福平,胡秀章,等.卵形頭部彈丸對混凝土靶板侵徹的二維數值模擬[J].彈道學報,2002,14(1):14-19. Li Yongchi,Yuan Fuping,Hu Xiuzhang,et al.The 2-D numerical simulation on penetrations of an oval headed projectile into concrete targets[J].Journal of Ballistics,2002,14(1):14-19.

[2] 晏麓暉,馮興民,夏清波,等.應變率和絕熱軟化對空腔膨脹影響的數值模擬[J].國防科技大學學報,2011,33(3): 44-47. Yan Luhui,Feng Xingmin,Xia Qingbo,et al.A numerical simulation of the effects of strain rate and adiabatic softening on the Cavity Expansion Model[J].Journal of National University of Defense Technology,2011,33(3):44-47.

[3] 趙攀峰,沈兆武,孫宇新.含損傷熱塑性材料靶板的抗沖塞研究[C]∥第十屆全國激波與激波管學術討論會論文集, 2002:141-146.

[4] Ning Jianguo,Ren Huilan,Guo Tingting,et al.Dynamic response of alumina ceramics impacted by long tungsten projectile[J].International Journal of Impact Engineering,2013,62:60-74.

[5] Lidén E,Mousavi S,Helte A,et al.Deformation and fracture of a long-rod projectile induced by an oblique moving plate:Numerical simulations[J].International Journal of Impact Engineering,2012,40/41:35-45.

[6] Iqbal M A,Gupta G,Diwakar A,et al.Effect of projectile nose shape on the ballistic resistance of ductile targets [J].European Journal of Mechanics—A/Solids,2010,29(4):683-694.

[7] 孫宇新,李永池,于少娟,等.長桿彈侵徹受約束A95陶瓷靶的實驗研究[J].彈道學報,2005,17(2):38-41. Sun Yuxin,Li Yongchi,Yu Shaojuan,et al.An experimental study on the penetration confined A95 ceramic targets[J].Journal of Ballistics,2005,17(2):38-41.

[8] 孫宇新,張進,李永池,等.內爆加載下熱塑性管殼的應力波演化與層裂效應研究[J].高壓物理學報,2005,19(4): 319-324. Sun Yuxin,Zhang Jin,Li Yongchi,et al.Propagation of stress wave and spallation of cylindrical tube under external explosive Loading[J].Chinese Journal of High Pressure Physics,2005,19(4):319-324.

[9] 李碩,王志軍,徐永杰,等.熱處理對彈體材料侵徹能力影響的分析[J].兵工學報,2014,35(S2):78-82. Li Shuo,Wang Zhijun,Xu Yongjie,et al.The effect of heat treatment on penetration performance of projectile material[J].Acta Armamentarii,2014,35(S2):78-82.

[10] 趙曉寧,何勇,張先鋒,等.A3鋼抗高速桿彈侵徹的數值模擬與實驗研究[J].南京理工大學學報,2011,35(2):164-167. Zhao Xiaoning,He Yong,Zhang Xianfeng,et al.Experimental and numerical study on A3 steel targets penetrated by high-velocity long-rod projectiles[J].Journal of Nanjing University of Science&Technology,2011,35(2): 164-167.

[11] 卞梁,王肖鈞,章杰.SPH/FEM耦合算法在陶瓷復合靶抗侵徹數值模擬中的應用[J].高壓物理學報,2010,24 (3):161-167. Bian Liang,Wang Xiaojun,Zhang Jie.Numerical simulations of antipenetration of confined ceramic targets by SPH/FEM coupling method[J].Chinese Journal of High Pressure Physics,2010,24(3):161-167.

[12] 楊震琦,龐寶君,王立聞,等.JH-2模型及其在Al2O3陶瓷低速撞擊數值模擬中的應用[J].爆炸與沖擊,2010,30 (5):463-471. Yang Zhenqi,Pang Baojun,Wang Liwen,et al.JH-2 model and its application to numerical simulation on Al2O3ceramic under low-velocity impact[J].Explosion and Shock Waves,2010,30(5):463-471.

[13] 任會蘭,陳雯,郭婷婷.陶瓷靶抗侵徹特性的數值模擬研究[J].北京理工大學學報(自然科學版),2013,33(2):111-115. Ren Huilan,Chen Wen,Guo Tingting.Numerical simulation on the anti-penetration properties of ceramic target [J].Transactions of Beijing Institute o Technology(Natural Science Edition),2013,33(2):111-115.

Influence of heat transfer on long-rod projectiles penetrating into ceramic targets

Li Ruiyu1,Sun Yuxin1,Zhou Ling2,Sun Qiran1, Zhao Yayun1,Feng Jiangtuo1
(1.National Key Laboratory of Transient Physics,Nanjing University of Science and Technology,Nanjing210094,Jiangsu,China; 2.China Academy of Ordnance Science,Beijing100000,China)

Based on the finite element method,the heat conduction equation was made discrete and written as the heat transfer computation code which was then embedded into the existing impact dynamics program.The new program was applied to the numerical analysis of the long-rod projectile penetrating into AD95 ceramic targets in the range of 900-1 800 m/s,and the influence of heat transfer on penetration capability was examined.Calculations show that the calculated penetration depth is less than that by the adiabatic model when the heat transfer is taken into account in the range of 900-1 350 m/s.However,it is opposite when the velocity of the projectile comes in the range of 1 450-1 800 m/s.The results by the heat transfer model and the adiabatic model are close to each other in the range of 1 350-1 450 m/s.

penetration;heat transfer;finite element;ceramic

O385國標學科代碼:13035

:A

10.11883/1001-1455(2017)02-0332-07

(責任編輯 張凌云)

2015-09-25;

:2016-03-23

李芮宇(1991— ),男,博士研究生;

:孫宇新,yxsun01@163.com。