強(qiáng)動(dòng)載荷下鋼筋混凝土結(jié)構(gòu)計(jì)算模型簡(jiǎn)評(píng)*

高 飛王明洋張先鋒何 勇李猛深

(1.南京理工大學(xué)智能彈藥技術(shù)國(guó)防重點(diǎn)學(xué)科實(shí)驗(yàn)室,江蘇南京210094; 2.解放軍理工大學(xué)爆炸沖擊防災(zāi)減災(zāi)國(guó)家重點(diǎn)實(shí)驗(yàn)室,江蘇南京210007)

強(qiáng)動(dòng)載荷下鋼筋混凝土結(jié)構(gòu)計(jì)算模型簡(jiǎn)評(píng)*

高 飛1,王明洋1,2,張先鋒1,何 勇1,李猛深2

(1.南京理工大學(xué)智能彈藥技術(shù)國(guó)防重點(diǎn)學(xué)科實(shí)驗(yàn)室,江蘇南京210094; 2.解放軍理工大學(xué)爆炸沖擊防災(zāi)減災(zāi)國(guó)家重點(diǎn)實(shí)驗(yàn)室,江蘇南京210007)

針對(duì)侵徹、爆炸等強(qiáng)動(dòng)載作用下混凝土類結(jié)構(gòu)計(jì)算中涉及的狀態(tài)方程、變形破壞彈塑性本構(gòu)關(guān)系與強(qiáng)度準(zhǔn)則等關(guān)鍵問題,根據(jù)混凝土多組分特征,簡(jiǎn)述考慮介質(zhì)中孔隙壓縮的狀態(tài)模型及彈塑性變形破壞中動(dòng)態(tài)損傷演化模型,并在計(jì)算實(shí)驗(yàn)方法的基礎(chǔ)上,給出需要進(jìn)一步研究的建議。

本構(gòu)模型;孔隙演化;鋼筋混凝土;強(qiáng)動(dòng)載

用實(shí)驗(yàn)研究強(qiáng)動(dòng)載產(chǎn)生的各種現(xiàn)象時(shí),有時(shí)難以得到滿意的結(jié)果。工程方法同樣由于其應(yīng)用的局限性,也難以解決廣泛的實(shí)際問題。基于有限單元法的數(shù)值模擬技術(shù)和室內(nèi)模擬實(shí)驗(yàn)相結(jié)合的計(jì)算實(shí)驗(yàn)方法,成為研究復(fù)雜物理過程的有效手段。在數(shù)值模擬高速?zèng)_擊時(shí),關(guān)鍵是建立能描述介質(zhì)實(shí)際行為的本構(gòu)模型。在完整的沖擊理論中,應(yīng)考慮到塑性流動(dòng)和彈性變形、流變和硬化、蒸發(fā)和冷凝、相變動(dòng)力學(xué)和化學(xué)變化以及破壞過程中的材料微結(jié)構(gòu)變化和結(jié)構(gòu)變化對(duì)相互撞擊物體的物理力學(xué)特性和應(yīng)力應(yīng)變狀態(tài)的相互影響。由于對(duì)材料的實(shí)際性能(熱力學(xué)性能、強(qiáng)度性能、流變學(xué)性能)缺乏深入研究,尚沒有考慮上述全部因素的理論模型。實(shí)際應(yīng)用的各種模型,均不同程度的考慮了上述的物理過程。

盡管現(xiàn)今已出現(xiàn)了相當(dāng)多的模擬固體撞擊各種靶體(有整塊靶、多層靶等,靶材有金屬、陶瓷、復(fù)合材料)的研究[1-4],但是固體擊碎鋼筋混凝土板的問題仍然有待于揭示。現(xiàn)有文獻(xiàn)中關(guān)于鋼筋對(duì)物體與混凝土靶相互撞擊作用結(jié)果影響的研究論文很少。A.L.Isaev[5]給出了針對(duì)建立鋼筋混凝土物理/數(shù)學(xué)模型和理論研究的資料,該模型可用于解決相互撞擊的應(yīng)用問題,研究表明,混凝土靶的配筋能改善其承載能力,遏制整體破壞,但是對(duì)局部破壞特點(diǎn)的影響不大。已有研究結(jié)果證明自由表面附近的鋼筋分布,能夠提高一些靶對(duì)侵徹的抗力,但是這種改變配筋的效應(yīng)并不是很大,而且隨著配筋網(wǎng)深度的增大,這一效應(yīng)還會(huì)進(jìn)一步降低。有的文獻(xiàn)試圖在實(shí)驗(yàn)和理論研究的基礎(chǔ)上,得出混凝土配筋在物體侵徹典型的鋼筋混凝土靶的過程中能起很大的作用的結(jié)論值得商榷。

M.L.Wilkins[6]對(duì)考慮鋼筋彈塑性變形和混凝土各向異性強(qiáng)度特性時(shí)的鋼筋混凝土結(jié)構(gòu)應(yīng)變的計(jì)算方法,作了簡(jiǎn)單的介紹。本文中將簡(jiǎn)述變形固體與含有混凝土層和鋼筋混凝土層的結(jié)構(gòu)之間的相互沖擊問題的計(jì)算方法,包括考慮破壞的變形固體動(dòng)力學(xué)數(shù)學(xué)模型,并給出相關(guān)數(shù)值模擬與實(shí)驗(yàn)結(jié)果。

1 基本方程

描述在三維空間中占有一定體積V和界面Σ的多孔彈塑性介質(zhì)空間絕熱運(yùn)動(dòng)的方程組,包含了主要的守恒定律,有如下形式:

式中:t是時(shí)間,ρ為密度,u是速度矢量,E是比內(nèi)能,n是面元外法線的單位矢量,σ為柯西應(yīng)力張量。在研究介質(zhì)單元的變形時(shí),把體積和形狀變化有關(guān)的應(yīng)力分量分離,即表示為球形部分和偏量部分之和:σ=-pδ+S,式中p為靜水壓力,S為偏應(yīng)力張量。式(1)與材料狀態(tài)方程、本構(gòu)關(guān)系、強(qiáng)度理論及邊界條件一起構(gòu)成完備的定解方程組。為了正確描述材料的動(dòng)態(tài)響應(yīng),研究的關(guān)鍵是建立正確的物理模型,即找到合適的狀態(tài)方程與本構(gòu)關(guān)系[7]。

2 狀態(tài)方程

2.1 常用狀態(tài)方程簡(jiǎn)評(píng)

高速碰撞初期產(chǎn)生的沖擊壓力遠(yuǎn)遠(yuǎn)大于靶板的強(qiáng)度極限,狀態(tài)方程起主要作用。HJC狀態(tài)方程[8]描述靜水壓力和體積應(yīng)變之間的關(guān)系時(shí)分彈性段、過渡段和壓實(shí)段。RHT模型采用的狀態(tài)方程是W.Herrmann[9]提出的,它在一定程度上能夠描述混凝土的壓力和體積應(yīng)變關(guān)系,但仍是基于唯象的本構(gòu)方程,未能體現(xiàn)孔隙動(dòng)態(tài)演化的規(guī)律。Tu Zhenguo等[10]對(duì)常用的混凝土類材料模型,如:隨動(dòng)硬化模型、脆性損傷模型、GR(gebbeken and ruppert)模型、HJC模型、RHT模型等做了更詳細(xì)的分析。

2.2 混凝土孔隙演化狀態(tài)方程

混凝土作為一種非均質(zhì)、不連續(xù)的多相復(fù)合摩擦型材料,其主要成分包括:固體顆粒和水泥砂漿,以及兩者之間大量的微裂紋和微孔洞,這些微裂紋和微孔洞使得混凝土在強(qiáng)動(dòng)載下具有很強(qiáng)的可壓縮性,對(duì)材料的動(dòng)態(tài)力學(xué)性能影響很大,可把它當(dāng)作由固相基體和夾雜物氣孔組成的雙組分材料研究。假設(shè)氣孔的幾何特征近似于球形,其分布尺寸函數(shù)則用整個(gè)氣孔群的總體特征尺寸表示[11-12]。多孔介質(zhì)的比容V為基體比容Vm、氣孔比容Vp和裂紋開裂時(shí)形成的比容Vt三者之和[13-15],即V=Vm+Vp+Vt,材料的孔隙率用參數(shù)α表示[9]:α=V/Vm,初始孔隙率α0=V0/Vm。

2.2.1 裂紋演化規(guī)律

混凝土受力的彈性階段,隨靜水壓力和偏應(yīng)力增長(zhǎng),微缺陷發(fā)展并導(dǎo)致材料的微觀斷裂。此時(shí)孔隙包括初始孔洞容積和裂紋張開引起的裂隙,將裂紋擴(kuò)展準(zhǔn)則引入混凝土的計(jì)算[16],可計(jì)算裂紋比容:

式中:ν是基體材料泊松系數(shù),Gm是基體材料剪切模量,R是裂紋半徑,pm=αp是基體壓力,N是單位體積內(nèi)的裂紋數(shù)。假設(shè)損傷裂紋在形成碎片前孔洞容積是不變的,根據(jù)上式和初始孔隙率可得裂紋孔隙演化方程:

裂紋的發(fā)展規(guī)律可按下式計(jì)算:

2.2.2 孔洞壓縮和膨脹方程

(1)壓縮時(shí)孔洞演化方程。孔洞演化可分為孔洞壓縮和膨脹2種情況,采用M.M.Carroll等[11]、J.N.Johnson等[17]的研究方法,將材料當(dāng)做內(nèi)部?jī)H包含單個(gè)球形氣孔的顆粒介質(zhì),如圖1所示,氣孔周圍是混凝土基體,模型所含基體物質(zhì)體積、孔隙體積及初始孔隙率均與原物質(zhì)相同。

圖2是根據(jù)方程(6)得到的壓力孔隙率變化時(shí)顆粒材料的加載卸載曲線圖。

圖1 混凝土的孔隙演化等效模型Fig.1 A spherical model of porous concrete

圖2 初始孔隙率為α0時(shí)材料的壓力曲線Fig.2 Compression path in material with initial distentionα0

(2)膨脹時(shí)孔洞演化方程。材料的斷裂發(fā)展過程可通過粘塑性材料在拉應(yīng)力作用下氣孔的增長(zhǎng)過程來描述,所用模型與圖1相似,利用粘塑性材料的球形空腔膨脹模型推導(dǎo)了孔洞演化方程[17,19]:

當(dāng)慣性項(xiàng)Q2及α的時(shí)間效應(yīng)均忽略時(shí),為了計(jì)算的方便,式(7)可簡(jiǎn)化為:

2.2.3 混凝土狀態(tài)方程

在壓力p作用下混凝土的密度變化可分為2個(gè)部分:基體顆粒的壓縮或膨脹、孔隙率α的變化,狀態(tài)方程正是將上述兩因素疊加,這里采用Grüneisen型狀態(tài)方程。

假設(shè)混凝土基體材料沖擊波速D與質(zhì)點(diǎn)速度u滿足關(guān)系:

式中:c為基體聲速,q為線性關(guān)系的斜率。取Hugoniot壓縮曲線上的點(diǎn)為基點(diǎn),根據(jù)Grüneisen方程計(jì)算的狀態(tài)方程為:

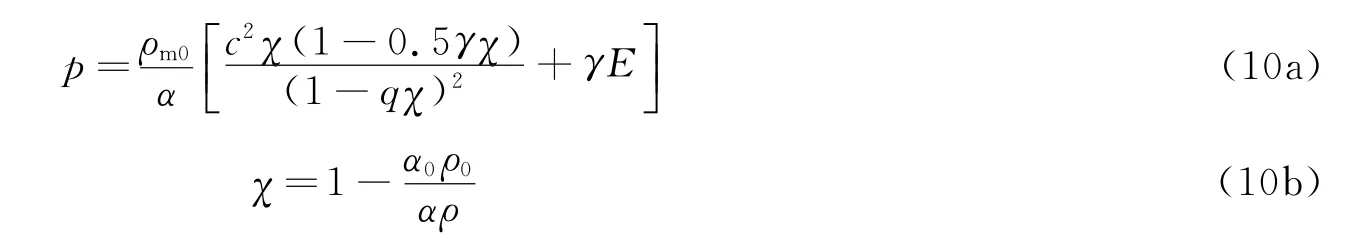
式中:γ為與基體材料對(duì)應(yīng)的Grüneisen系數(shù),ρm0為基體的初始密度,E為材料與ρ、p對(duì)應(yīng)的比內(nèi)能。上式需要補(bǔ)充孔隙率α的演化方程,在變形的彈性階段α的演化方程采用式(3),在變形的塑性階段采用式(6)或式(8)。

混凝土破壞后按帶孔隙的顆粒材料處理,此時(shí)不能承受拉應(yīng)力,拉伸時(shí)式(10a)變?yōu)?

壓縮時(shí)式(10)、(6)構(gòu)成了破壞后混凝土的狀態(tài)方程。

2.3 鋼筋混凝土混合物狀態(tài)方程

為了降低計(jì)算量,將鋼筋混凝土結(jié)構(gòu)看作混凝土層和鋼筋層的均勻二元混合物,簡(jiǎn)化模型如圖3。混合物初始密度ρ0=φ1ρ10+ φ2ρ20,其中:φ1、φ2、ρ10、ρ20分別為鋼筋和混凝土的初始體積分?jǐn)?shù)和密度,且φ1+φ2=1。體積分?jǐn)?shù)由垂直于鋼筋方向上的橫截面中鋼筋和混凝土所占的面積計(jì)算。

根據(jù)Hugoniot沖擊絕熱關(guān)系和Grüneisen方程可以得到鋼筋混凝土混合物狀態(tài)方程:

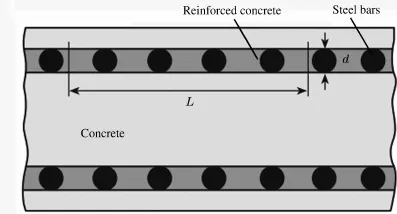
圖3 鋼筋混凝土結(jié)構(gòu)示意圖[20-21]Fig.3 Sketch of reinforced concrete[20-21]

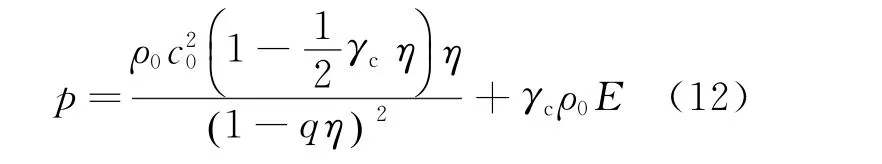
式中:η=1-ρ0Vc,Vc為混合物比容,γc為混合物Grüneisen系數(shù),E為比內(nèi)能。

c0、q為混合物中沖擊波速度D與質(zhì)點(diǎn)速度u線性關(guān)系式D=c0+qu中的系數(shù),且各組分的沖擊絕熱曲線滿足:

以p為變量的混合物絕熱曲線為:

式中:Vi0為鋼(i=1)和混凝土(i=2)的初始比容,mi=φiρi0/ρ0為鋼筋混凝土中鋼(i=1)和混凝土(i=2)的質(zhì)量分?jǐn)?shù)(m1+m2=1)。

利用混合物沖擊波的關(guān)系式:

可建立沖擊波速度與質(zhì)點(diǎn)速度的關(guān)系式,并確定系數(shù)c0、q。

混合物的Grüneisen系數(shù)γc可由各組分Grüneisen系數(shù)γi按下式確定:

破壞后的混合物,拉伸時(shí)狀態(tài)方程采用式(11),壓縮時(shí)采用式(12)、式(6)。

混合物的剪切模量G和流動(dòng)極限σT,由下式計(jì)算:

式中:Gi和σsi(i=1,2)分別為混合物各組分的剪切模量和流動(dòng)極限。

3 本構(gòu)模型

3.1 混凝土本構(gòu)模型

3.1.1 混凝土常用本構(gòu)模型簡(jiǎn)評(píng)

在沖擊載荷作用下,混凝土內(nèi)部會(huì)發(fā)生壓縮和拉伸應(yīng)力波的相互作用,在材料內(nèi)部產(chǎn)生不同性質(zhì)和不同程度的內(nèi)部損傷和破壞,對(duì)材料性能產(chǎn)生復(fù)雜的影響[22]。到目前為止,還沒有一種模型可以用來完全描述混凝土的本構(gòu)關(guān)系[23-30]。因此,適用于沖擊問題的混凝土本構(gòu)模型需要包含對(duì)動(dòng)態(tài)效應(yīng)、內(nèi)部拉伸和壓縮損傷以及各種復(fù)雜應(yīng)力狀態(tài)等影響因素的合理描述[31]。當(dāng)前HJC[8]本構(gòu)模型、RHT[32]本構(gòu)模型、L.J.Malvar等[33]提出的本構(gòu)模型依然是混凝土在沖擊載荷下應(yīng)用最廣泛的模型。M.Polanco-loria等[34]在HJC模型基礎(chǔ)上進(jìn)行了改進(jìn),稱為MHJC模型。MHJC模型引入加載路徑相關(guān)性,考慮了J3的影響,修正了應(yīng)變率效應(yīng)、強(qiáng)度面和損傷函數(shù)等。改進(jìn)了應(yīng)變率影響系數(shù)的收斂性,對(duì)損傷的刻畫也更為細(xì)致,但還是沒有深入考慮拉伸損傷對(duì)混凝土的影響,TCK模型[35]則對(duì)拉伸損傷情況有較好的處理。王麗穎等[36]用RHT模型成功模擬了彈丸高速侵徹混凝土靶時(shí)靶體的損傷破壞過程。上述模型中僅單獨(dú)考慮了在體積拉伸或壓縮條件下的損傷效應(yīng),而沒有考慮二者共同作用下混凝土的損傷效應(yīng)。為此,不少研究者利用兩種不同模型各自的優(yōu)勢(shì)構(gòu)造組合模型,得到了一個(gè)能較好反映混凝土損傷情況的模型,包括武海軍等[37]、金乾坤[38]、馬愛娥等[39]、魏強(qiáng)等[40-41]的研究工作。

3.1.2 混凝土應(yīng)力應(yīng)變關(guān)系

當(dāng)混凝土處于彈性階段時(shí),應(yīng)力應(yīng)變關(guān)系按滿足廣義虎克定律的各向同性線彈性材料處理,材料進(jìn)入塑性后,對(duì)應(yīng)變速率張量分離,根據(jù)正交流動(dòng)法則:

將式(20)代入式(18)并將體應(yīng)變分離:

對(duì)式(21a)兩邊同乘以S,并根據(jù)加卸載條件可得到λ值:

剪切模量G與α及混凝土基體的剪切模量Gm相關(guān)[19]:

3.2 鋼筋本構(gòu)及其與混凝土的粘結(jié)關(guān)系

鋼筋混凝土結(jié)構(gòu)中,通常將鋼筋看成輔助強(qiáng)化材料,起遏制靶體整體破壞的作用,對(duì)侵深及彈體剩余速度影響不大。鋼筋作為傳統(tǒng)金屬材料,無論是靜載荷還是動(dòng)力載荷作用下,其本構(gòu)關(guān)系都較為明確,此處不再贅述。

一系列研究表明[42],沖擊加載對(duì)鋼筋與混凝土粘結(jié)力有較大影響,隨著應(yīng)變速率的提高,鋼筋與混凝土的粘結(jié)力大大提高。這個(gè)結(jié)論表明了粘結(jié)力的主要因素是由于鋼筋與混凝土的機(jī)械咬合,其強(qiáng)度取決于微裂紋的發(fā)展。快速加載時(shí),微裂紋的發(fā)展延遲,強(qiáng)度因而提高,但提高量不大。在彈體侵徹鋼筋混凝土靶過程中,侵徹近區(qū)靶體處于一維應(yīng)變狀態(tài),由于圍壓造成的靶體強(qiáng)度提高較大,故而認(rèn)為鋼筋的作用不明顯,而且隨著配筋網(wǎng)逐漸深入混凝土內(nèi)部,這一效應(yīng)還會(huì)降低的更多。為了簡(jiǎn)化數(shù)值計(jì)算模型,把鋼筋混凝土看作混合物處理,假設(shè)在同一速度場(chǎng)與加速度場(chǎng)中,鋼筋與混凝土之間不發(fā)生滑移,所以不單獨(dú)考慮鋼筋與混凝土的粘結(jié)關(guān)系。Q.M.Li等[43-44]認(rèn)為較低或適度配筋時(shí),鋼筋對(duì)于侵徹和層裂的影響很小,而較高配筋時(shí)鋼筋也僅僅是提高穿甲時(shí)的阻力。在第5節(jié)給出計(jì)算驗(yàn)證時(shí),計(jì)算結(jié)果表明是否考慮鋼筋的作用對(duì)侵深造成的差異不超過8%。因此,當(dāng)采用計(jì)算實(shí)驗(yàn)方法時(shí),把鋼筋混凝土當(dāng)作均勻二元混合物來研究,可以縮短大量的計(jì)算時(shí)間,同時(shí),這種近似處理對(duì)數(shù)值結(jié)果的分析也不會(huì)出現(xiàn)本質(zhì)上的差別。

3.3 鋼筋混凝土混合物應(yīng)力應(yīng)變關(guān)系

當(dāng)混合物處于彈性階段時(shí),應(yīng)力應(yīng)變關(guān)系按滿足廣義虎克定律的各向同性線彈性材料處理,進(jìn)入塑性后,按滿足正交流動(dòng)法則的各向同性均勻材料處理,其應(yīng)力應(yīng)變關(guān)系仍可統(tǒng)一表示為式(21)～(22)的形式。

4 強(qiáng)度理論

針對(duì)混凝土類脆性材料,T.Jankowiak等[45]從塑性條件和破壞準(zhǔn)則兩方面,對(duì)Mohr-Coulomb準(zhǔn)則、Drucker-Parger準(zhǔn)則、Burzyński能量準(zhǔn)則、Bresler-Pister準(zhǔn)則等進(jìn)行了細(xì)致的研究,認(rèn)為對(duì)材料強(qiáng)度合理的描述,不僅要考慮壓縮情況,而且也應(yīng)很好的體現(xiàn)拉伸以及應(yīng)變率效應(yīng)。

4.1 混凝土強(qiáng)度準(zhǔn)則

強(qiáng)度準(zhǔn)則采用基于經(jīng)驗(yàn)的唯象模型,設(shè)混凝土基體的極限面為:

根據(jù)能量原理,孔隙率為α的混凝土極限面為:

采用兩個(gè)極限面分別表述混凝土的最大強(qiáng)度面和破壞后喪失粘聚力混凝土的強(qiáng)度面,式(25a)中:

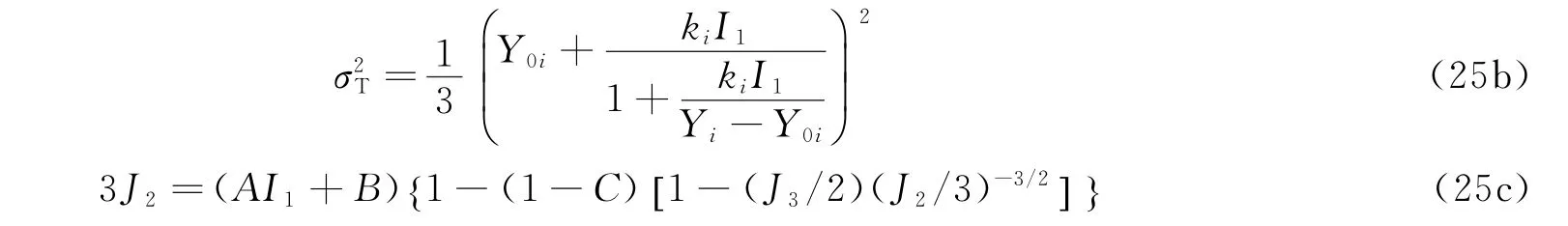
式中:Yi為剪切強(qiáng)度的極限值,Y0i為粘聚力相關(guān)參數(shù),ki為內(nèi)摩擦角相關(guān)參數(shù),i=1,2分別代表未損傷的混凝土和破壞后的混凝土。I1、J2、J3分別是第一應(yīng)力張量不變量,第二、第三應(yīng)力偏量不變量;分別是單軸壓縮、拉伸和純剪時(shí)的強(qiáng)度極限。

材料由最大強(qiáng)度面1向殘余強(qiáng)度面2的跌落,是由剪切破壞和拉伸斷裂引起的。壓應(yīng)力作用下的破壞準(zhǔn)則是塑性應(yīng)變強(qiáng)度eu達(dá)到極限值[46],即:

式中:T1、T2分別為應(yīng)變張量第一、第二不變量,當(dāng)eu達(dá)到臨界值時(shí),材料破壞并進(jìn)入極限面2。在拉應(yīng)力作用下,有損傷裂紋材料的斷裂破壞準(zhǔn)則是當(dāng)相對(duì)孔隙體積達(dá)到臨界值ξ*=(α*-1)/α*,材料破壞并進(jìn)入極限面2。

4.2 鋼筋混凝土混合物強(qiáng)度準(zhǔn)則

與混凝土不同的是,鋼筋混凝土的混合物按彈塑性材料處理,滿足Mises屈服條件:

式中:σT為鋼筋混凝土混合物的流動(dòng)極限。

混合物的破壞可分為拉伸斷裂和剪切破壞兩類。當(dāng)混合物的孔隙率α達(dá)到臨界值時(shí)材料發(fā)生拉伸斷裂,與混凝土不同,混合物的孔隙演化完全由式(6)～(7)控制。與混凝土相似相似的是,材料剪切破壞的判據(jù)是塑性應(yīng)變相關(guān)參數(shù)eu達(dá)到極限值。

破壞后的混合物按帶孔隙的顆粒材料處理,此時(shí)材料不能承受拉應(yīng)力,僅能承受壓應(yīng)力和剪應(yīng)力,其極限面采用式(25)的形式。

5 實(shí)驗(yàn)與計(jì)算驗(yàn)證

根據(jù)文中考慮混凝土裂紋擴(kuò)展與孔洞演化的本構(gòu)模型,N.N.Belov等[13,14,47]、S.A.Afanas’eva等[20]模擬計(jì)算了不同頭部形狀鋼彈丸對(duì)混凝土和鋼筋混凝土靶的侵徹問題。

5.1 平頭彈垂直侵徹混凝土實(shí)驗(yàn)與數(shù)值模擬

侵徹實(shí)驗(yàn)中,彈丸是直徑d0=0.76 cm,質(zhì)量為8.1 g的平頭圓柱鋼彈,速度為130～700 m/s,混凝土靶厚200 mm。圖4(a)為鋼彈以370 m/s速度沖擊后,混凝土板正面的照片,彈坑直徑等于5.3d0。

圖4 鋼彈以370 m/s速度沖擊混凝土板實(shí)驗(yàn)與數(shù)值模擬結(jié)果[13]Fig.4 Interaction between a model projectile and concrete plates at initial impact velocity of 370 m/s[13]

圖4(b)所示為數(shù)值模擬中彈體完全停止時(shí)混凝土的破壞情況,這與實(shí)驗(yàn)結(jié)果是定性吻合的:彈坑形狀、正面有崩落、彈體未變形,計(jì)算涉及的有關(guān)材料與模型參數(shù)參考文獻(xiàn)[14]。在速度為370 m/s時(shí),侵徹深度P的計(jì)算值相對(duì)于實(shí)驗(yàn)值誤差為5%,彈坑直徑D的計(jì)算值相對(duì)于實(shí)驗(yàn)值誤差為13%,可見計(jì)算結(jié)果與實(shí)驗(yàn)結(jié)果吻合較好。圖5所示為彈體在混凝土靶中侵深P與初速v0之間的關(guān)系。

圖5 彈體在混凝土靶中侵深與初速之間的關(guān)系[14]Fig.5 Relation between the penetration depth and the initial impact velocity[14]

5.2 平頭彈侵徹混凝土和鋼筋混凝土靶比較

模型彈為長(zhǎng)度與直徑相等的(h=d=300 mm)平頭鋼彈,彈丸初速均為300 m/s。靶體分混凝土和鋼筋混凝土靶板兩種,厚度均為H0=600 mm,鋼筋混凝土的配筋是兩層間距為120×120 mm鋼筋網(wǎng),鋼筋直徑為32 mm,鋼筋網(wǎng)相對(duì)于板的中面對(duì)稱布置,嵌入混凝土的厚度為30 mm。

圖6分別展示了彈丸在4.2、5.2 ms穿透混凝土和鋼筋混凝土?xí)r對(duì)稱面的投影圖。表1給出靶中侵徹深度與時(shí)間對(duì)應(yīng)關(guān)系,彈丸穿透鋼筋混凝土所需時(shí)間比混凝土長(zhǎng),分別為5.2、4.3 ms,就2種靶的相對(duì)侵徹深度P/d而言,混凝土比鋼筋混凝土稍大,但相差不大(小于8%),表明自由表面附近的鋼筋分布能夠提高靶的抗侵徹能力,但配筋的影響并不是很大,而且隨著配筋網(wǎng)深度的增大,這一影響還會(huì)降低得更多。

圖6 平頭彈穿透靶的數(shù)值模擬[20]Fig.6 Simulation of the penetration process[20]

表1 不同時(shí)刻靶中P/d比較[20]Table 1 Comparison ofP/dat different times[20]

5.3 卵形彈侵徹鋼筋/混凝土間隔靶實(shí)驗(yàn)與數(shù)值模擬

彈丸總長(zhǎng)度為81 mm,直徑為23 mm,其中卵形頭部直徑為14 mm。靶體為鋼筋/混凝土間隔靶(共3組),每一組由3層組成,第1、3層為鋼筋混凝土層且厚度均為hrc,第2層為鋼板且厚度為hst。那么一組鋼筋/混凝土間隔靶厚度等于62.5 mm,其中hrc=30 mm,hst=2.5 mm。一般而言,在708～1 447 m/s的速度范圍內(nèi),彈丸可以穿透2組鋼筋/混凝土間隔靶,穿入第3組時(shí)彈丸便停止侵徹,總的侵徹深度P＜155 mm。圖7給出了在速度為1 230 m/s時(shí),靶后破壞示意圖,圖8為數(shù)值模擬時(shí)彈靶作用過程。當(dāng)速度增加到1 573 m/s,彈丸可以穿透3組,此時(shí)總的侵徹深度P=187.5 mm。

圖7 模型彈侵徹鋼筋/混凝土間隔靶背面視圖[47]Fig.7 Rear view of steel-concrete plates after the impact with a projectile[47]

圖8 模型彈對(duì)鋼筋/混凝土間隔靶侵徹過程[47]Fig.8 Interaction between a model projectile and steel-reinforced plates[47]

6 結(jié)論與建議

(1)強(qiáng)動(dòng)載下混凝土類脆性材料的動(dòng)態(tài)響應(yīng)總是伴隨著微孔洞和微裂紋的變化,必須考慮其可壓縮性。

(2)強(qiáng)動(dòng)載下對(duì)混凝土類脆性材料的破壞過程研究,不僅要考慮材料初始彈性階段的脆性斷裂破壞,而且要考慮達(dá)到裂紋尺寸臨界值的強(qiáng)度準(zhǔn)則后材料的粘塑性破壞。

(3)孔隙演化模型驗(yàn)證研究。將混凝土視為多相復(fù)合介質(zhì),等價(jià)為含氣孔的單個(gè)球形顆粒介質(zhì)處理,將涉及孔洞演化與裂紋擴(kuò)展的本構(gòu)模型植入有限元軟件二次開發(fā),驗(yàn)證模型的合理性,為該模型在陶瓷、巖石等材料的成功應(yīng)用奠定基礎(chǔ)。

(4)參數(shù)物理意義與實(shí)驗(yàn)設(shè)計(jì)研究。模型中涉及許多材料參數(shù),研究現(xiàn)有參數(shù)的物理意義,無論是對(duì)更深層次的理解模型的本質(zhì),還是對(duì)后續(xù)的實(shí)驗(yàn)設(shè)計(jì)參數(shù)的獲取,都顯得十分必要。此外,通過相關(guān)沖擊與爆炸實(shí)驗(yàn)研究可進(jìn)一步驗(yàn)證模型的可靠性。

(5)開展較寬速度范圍內(nèi)模型適用性研究。有學(xué)者雖已對(duì)模型進(jìn)行一系列實(shí)驗(yàn)驗(yàn)證,并取得了較為滿意的結(jié)果,但是實(shí)驗(yàn)中侵徹速度最高只有1 573m/s。隨著超高速鉆地武器的發(fā)展,侵徹速度一般都達(dá)到了2～3 km/s,甚至更高,在超高速侵徹時(shí)模型的有效性與可行性也是值得考慮的問題。

參考文獻(xiàn):

[1] Fomin V M,Gulidov A I,Sapozhnikov G A,et al.High-speed interaction of solids[M].Novosibirsk:Sib.Otd. Ross.Akad.Nauk,1999.

[2] Belov N N,Demidov V N,Efremova L V,et al.Computer modeling of the dynamics of high-velocity impact and accompanying physical phenomena[J].Russian Physics Journal,1992,35(8):690-723.

[3] НиколаевскогоВН.Высокоскоростныеударныеявления[M].Москва:Мир,1973.

[4] ГригорянаСС.Динамикаудара[M].Москва:Мир,1985.

[5] Isaev A L.Effect of concrete reinforcement on the results of dynamic loading by penetrating bodies[C]∥Proceedings of the 3th International Conference of Khariton Scientific Readings in Extremal State of Material Detonation Shock Waves.Sarov,Russia,2002:150-156

[6] Wilkins M L.Computational methods in fluid dynamics[M].Moscow:Mir,1967:212-263.

[7] 朱建士,胡曉棉,王裴,等.爆炸與沖擊動(dòng)力學(xué)若干問題研究進(jìn)展[J].力學(xué)進(jìn)展,2010,40(4):400-423. Zhu Jianshi,Hu Xiaomian,Wang Pei,et al.A review on research progress in explosion and mechanics and impact dynamics[J].Advances in Mechanics,2010,40(4):400-423.

[8] Holmquist T J,Johnson G R.A computational constitutive model for concrete subjected to large strains,high strain rates and high pressure[C]∥Proceedings of the 14th International Symposium on Ballistics.Quebec,Canada,1993:591-600.

[9] Herrmann W.Constitutive equation for the dynamic compaction of ductile porous materials[J].Journal of Applied Physics,1969,40(6):2490-2499.

[10] Tu Zhenguo,Lu Yong.Evaluation of typical concrete material models used in hydrocodes for high dynamic response simulations[J].International Journal of Impact Engineering,2009,36(1):132-146.

[11] Carroll M M,Holt A C.Static and dynamic porecollapse relations for ductile porous materials[J].Journal of Applied Physics,1972,43(4):1626-1636.

[12] Bhatt J J,Carroll M M,Schatz J F.A spherical model calculation for volumetric response of porous rocks[J]. Journal of Applied Mechanics,1975,42(2):363-368.

[13] Belov N N,Dzyuba P V,Kabantsev O V,et al.Mathematical modeling of dynamic fracture processes in concrete [J].Mechanics of Solids,2008,43(2):269-276.

[14] Belov N N,Kabantsev O V,Konyaev A A,et al.Analysis of reinforced-concrete strength under impact loading [J].Journal of Applied Mechanics and Technical Physics,2006,47(6):911-917.

[15] Belov N N,Yugov N T,Kopanitsa D G,et al.Calculation of the strength of reinforced concrete columns under repeated longitudinal impact[J].Journal of Applied Mechanics and Technical Physics,2008,49(1):148-155.

[16] Lynn S,Donald R C,Donald A S.Computational models for ductile and brittle fracture[J].Journal of Applied Physics,1976,47(11):4814-4826.

[17] Johnson J N.Dynamic fracture and spallation in ductile solids[J].Journal of Applied Physics,1981,52(4):2812-2825.

[18] Afanas’eva S A,Belov N N,Yugov N T.The penetration of cylindrical strikes through obstacles made of concrete and sandy ground[J].Doklady Physics,2002,47(12):876-879.

[19] Belov N N,Demidov V N,Efremova L V,et al.Computer modeling of the dynamics of high-velocity impact and accompanying physical phenomena[J].Russian Physics Journal,1992,35(8):690-723.

[20] Afanas’eva S A,Belov N N,Kopanitsa D G,et al.Failure of concrete and reinforced-concrete plates under highspeed shock and explosion[J].Doklady Physics,2005,50(3):132-135.

[21] Belov N N,Yugov N T,Kopanitsa D G,et al.Stress analysis of concrete and reinforced-concrete slab structures under a high-velocity impact[J].Journal of Applied Mechanics and Technical Physics,2005,46(3):444-451.

[22] 王政,倪玉山,曹菊珍,等.沖擊載荷下混凝土動(dòng)態(tài)力學(xué)性能研究進(jìn)展[J].爆炸與沖擊,2005,25(6):519-527. Wang Zheng,Ni Yushan,Cao Juzhen,et al.Recent advances of dynamic mechanical behavior of concrete under impact loading[J].Explosion and Shock Waves,2005,25(6):519-527.

[23] 陳書宇.一種混凝土損傷模型和數(shù)值方法[J].爆炸與沖擊,1998,18(4):349-357. Chen Shuyu.A concrete damage model and numerical methods[J].Explosion and Shock Waves,1998,18(4): 349-357.

[24] 過鎮(zhèn)海,王傳志.多軸應(yīng)力下混凝土的強(qiáng)度和破壞準(zhǔn)則研究[J].土木工程學(xué)報(bào),1991,24(3):1-14. Guo Zhenhai,Wang Chuanzhi.Investigation of strength and failure criterion of concrete under multiaxial stresses [J].China Civil Engineering Journal,1991,24(3):1-14.

[25] 胡時(shí)勝,王道榮.沖擊載荷下混凝土材料的動(dòng)態(tài)本構(gòu)關(guān)系[J].爆炸與沖擊,2002,22(3):242-246. Hu Shisheng,Wang Daorong.Dynamic constitutive relation of concrete under impact[J].Explosion and Shock Waves,2002,22(3):242-246.

[26] 宋偉,袁勇.單調(diào)軸向荷載下鋼筋混凝土拉伸損傷本構(gòu)研究[J].工程力學(xué),2005,22(6):142-147. Song Wei,Yuan Yong.Damaging constitutive law of reinforced concrete specimens under monotonic uniaxial tensile load[J].Engineering Mechanics,2005,22(6):142-147.

[27] 商霖,寧建國(guó),孫遠(yuǎn)翔.強(qiáng)沖擊載荷作用下鋼筋混凝土本構(gòu)關(guān)系的研究[J].固體力學(xué)學(xué)報(bào),2005,26(2):175-181. Shang Lin,Ning Jianguo,Sun Yuanxiang.The constitutive relationship of reinforced concrete subjected to shock loading[J].Chinese Journal of Solid Mechanics,2005,26(2):175-181.

[28] 路德春,杜修力,閆靜茹,等.混凝土材料三維彈塑性本構(gòu)模型[J].中國(guó)科學(xué):技術(shù)科學(xué),2014(8):288-291. Lu Dechun,Du Xiuli,Yan Jingru,et al.A three-dimensional elastoplastic constitutive model for concrete[J].Scientia Sinica Techologica,2014(8):288-291.

[29] Grady D E,Kipp M E.Continuum modeling of explosive fracture in oil shale[J].International Journal of Rock Mechanics and Mining Science,1980,17(6):147-157.

[30] Forrestal M J,Luk V K,Watts H A.Penetration of reinforced concrete with ogive-nose penetrators[J].International Journal of Solids and Structures,1988,24(1):77-87.

[31] 王政,倪玉山,曹菊珍,等.沖擊載荷下混凝土本構(gòu)模型構(gòu)建研究[J].高壓物理學(xué)報(bào),2006,26(4):337-344. Wang Zheng,Ni Yushan,Cao Juzhen,et al.Building of a constitutive model for concrete under dynamic impact [J].Chinese Journal of High Pressure Physics,2006,26(4):337-344.

[32] Heider N,Hiermaier S.Numerical simulation of tandem warheads[C]∥Proceedings of the 19th International Symposium on Ballistics.Interlaken,Switzerland:IBS 2001 Symposium Office,2001:1493-1499.

[33] Malvar L J,Crawford J E,Wesevich J W,et al.A plasticity concrete material model for DYNA3D[J].International Journal of Impact Engineering,1997,19(9):847-873.

[34] Polanco-loria M,Hopperstad O S,B?rvik T,et al.Numerical predictions of ballistic limits for concrete slabs using a modified version of the HJC concrete model[J].International Journal of Impact Engineering,2008,35(5): 290-303.

[35] Taylor L M,Chen E P,Kuszmaul J S.Microcrack-induced damage accumulation in brittle rock under dynamic loading[J].Journal of Computer Methods in Applied Mechanics and Engineering,1986,55(3):301-320.

[36] 王麗穎,蔣建偉,門建兵.混凝土穿孔過程的數(shù)值模擬[C]∥計(jì)算爆炸力學(xué)理論、方法及工程應(yīng)用暨第二屆全國(guó)計(jì)算爆炸力學(xué)會(huì)議錄.北京理工大學(xué)出版社,2002:228-234.

[37] 武海軍,黃風(fēng)雷,金乾坤,等.彈體貫穿鋼筋混凝土數(shù)值模擬[J].爆炸與沖擊,2003,23(6):545-550. Wu Haijun,Huang Fenglei,Jin Qiankun,et al.Numerical simulation on perforation of reinforced concrete targets [J].Explosion and Shock Waves,2003,23(6):545-550.

[38] 金乾坤.混凝土動(dòng)態(tài)損傷與失效模型[J].兵工學(xué)報(bào),2006,27(1):10-14. Jin Qiankun.Dynamic damage and failure model for concrete materials[J].Acta Armamentarii,2006,27(1):10-14.

[39] 馬愛娥,黃風(fēng)雷,初哲,等.彈體攻角侵徹混凝土數(shù)值模擬[J].爆炸與沖擊,2008,28(1):33-37. Ma Aie,Huang Fenglei,Chu Zhe,et al.Numerical simulation on yawed penetration into concrete[J].Explosion and Shock Waves,2008,28(1):33-37.

[40] 魏強(qiáng),蔣建偉,黃西成,等.混凝土損傷組合模型[J].固體力學(xué)學(xué)報(bào),2011,32(S1):416-421. Wei Qiang,Jiang Jianwei,Huang Xicheng,et al.Combined damage model of concrete[J].Chinese Journal of Sol-id Mechanics,2011,32(S1):416-421.

[41] 魏強(qiáng),黃西成,顏怡霞,等.混凝土動(dòng)態(tài)損傷模型[C]∥第十屆全國(guó)沖擊動(dòng)力學(xué)學(xué)術(shù)會(huì)議論文集,2011,1-7.

[42] 錢七虎,王明洋.高等防護(hù)結(jié)構(gòu)計(jì)算理論[M].南京:江蘇科學(xué)技術(shù)出版社,2009.

[43] Li Q M,Chen X W.Dimensionless formulae for penetration depth of concrete target impacted by a non-deformable projectile[J].International Journal of Impact Engineering,2003,28(1):93-116.

[44] Li Q M,Reid S R,Wen H M,et al.Local impact effects of hard missiles on concrete targets[J].International Journal of Impact Engineering,2005,32(1):224-284.

[45] Jankowiak T,Lodygowski T.Handbook of damage mechanics[M].New York:Springer Press,2014.

[46] Belov N N,Yugov N T,Afanas’eva S A,et al.Mathematical modeling of deformation and fracture for bony tissues in the case of high-speed impact[J].Doklady Physics,2011,56(3):190-193.

[47] Belov N N,Yugov N T,Afanas’eva S A,et al.Strength of a reinforced-concrete commercial object on high-velocity impact with a model projectile[J].Journal of Engineering Physics and Thermophysics,2014,87(2):420-426.

A comment on the calculation models for reinforced concrete under intense dynamic loading

Gao Fei1,Wang Mingyang1,2,Zhang Xianfeng1,He Yong1,Li Mengshen2
(1.Ministerial Key Laboratory of ZNDY,Nanjing University of Science and Technology,Nanjing210094,Jiangsu,China; 2.State Key Laboratory for Disaster Prevention&Mitigation of Ex plosion&Impact,PLA University of Science and Technology,Nanjing210007,Jiangsu,China)

Based on several key issues of the elastic-plastic constitutive model,the equation of state and strength criterion,and the calculation of the strength of concrete under blast and impact loading were reviewed.Concrete being viewed as a binary material composed of matrix and pores,a model including the pore compaction and dynamic damage evolution in elastic-plastic deformation and failure were introduced.On the basis of a mathematical-experimental method,some conclusions and proposals for further reseach were made at the end of the paper.

constitutive model;porosity evolution;reinforced concrete;intense dynamic loading

O385國(guó)標(biāo)學(xué)科代碼:1303530

:A

10.11883/1001-1455(2017)02-0365-12

(責(zé)任編輯 王易難)

2015-05-20;

:2015-09-18

國(guó)家自然科學(xué)基金項(xiàng)目(51508568);國(guó)家重點(diǎn)實(shí)驗(yàn)室開放基金資助項(xiàng)目(DPMEIKF201405);江蘇省重點(diǎn)實(shí)驗(yàn)室開放基金項(xiàng)目(3092014012200401)

高 飛(1990— ),男,博士研究生;

:王明洋,wmyrf@163.com。