例談“設且求”思想在解題中的應用

廣東省興寧市第一中學(514500) 藍云波

例談“設且求”思想在解題中的應用

廣東省興寧市第一中學(514500) 藍云波

在高中數學中,“設而不求”是非常重要的一種數學思想,這種思想方法是在解題過程中,由于要使用到某個方程的根,但卻并不直接求出,而是通過設出未知數,并借助一定的手段進行消元或代換的一種思想方法.這個設出的未知數起到非常重要的橋梁作用.筆者在教學過程中發現,這種思想方法主要應用在導數與解析幾何中.雖然這種思想方法具有重要的價值,但從解題的角度講,這是一種迂回曲折的方法.學生在學習的過程中,也曾提問過筆者,對通常涉及二次方程的設而不求問題,是否一定要借助設而不求的思想,如果可以不使用這種方法,如何突破解題的瓶頸.這個問題引起了筆者的注意,于是從求根的視角重新審視了這類問題.由于使用二次方程的求根公式求出的根較為復雜,是“暴力”地求出方程的根,可稱作“設且求”思想.現筆者從導數和解析幾何方面作一些探索,現分析如下,供大家參考.

一、導數中的應用

某些函數的極值問題,求導之后發現極值點是二次方程的根,但此二次方程的根較為復雜,只能用求根公式求解.筆者發現,常見的做法并不是使用求根公式求出二次方程的根,因為方程的根顯得較為復雜,似乎不利于問題的求解,常見的做法仍然是設而不求或分類討論.筆者發現,這類問題,使用求根公式也是一種通法,關鍵在于實施計算強行求解,或借助換元,發掘新的未知數與參數的關系式,然后利用整體代換的思想并構造新的函數進行分析,此時問題可能反而變得簡單.

例1設函數(a∈R).

(1)若f(x)在x=0處取得極值,確定a的值,并求此時曲線y=f(x)在點(1,f(1))處的切線方程;

(2)若f(x)在[3,+∞)上為減函數,求a的取值范圍.

解析(1)略;(2)

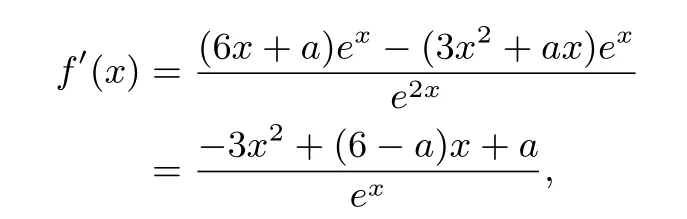
方程-3x2+(6-a)x+a=0的判別式

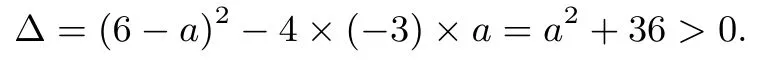
令f′(x)=0得,

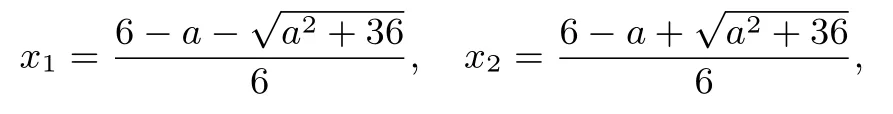
且x1＜ x2.當x∈(-∞,x1)時,f′(x)＜ 0,f(x)單調遞減;當x∈(x1,x2)時,f′(x)＞ 0,f(x)單調遞增;當x∈(x2,+∞)時,f′(x)＜0,f(x)單調遞減.所以函數f(x)的減區間為(-∞,x1]和[x2,+∞).要使f(x)在[3,+∞)上為減函數,則必有x2≤3,即,解得a≥-.所以a的取值范圍為.

點評本題在求出導函數之后,可轉化為二次方程-3x2+(6-a)x+a=0在(3,+∞)上沒有實根,并借助根的分布,通過設而不求和二次方程的根的分布解決.而本文給出的解法,直接“暴力”求出實根,通過強行計算解答,整個過程相當直觀且易于理解,干凈利索并具有直搗黃龍之妙!且運算并不復雜,是一種自然的解法.

例2已知函數f(x)=lnx-ax2+x,a∈R.

(1)求函數f(x)的單調區間;

(2)是否存在實數a,使得函數f(x)的極大值大于0.若存在,求出a的值;若不存在,請說明理由.

解析(1)略;

(2)由(1)可知,f(x)有極值,則a＞0且f(x)有極大值無極小值,

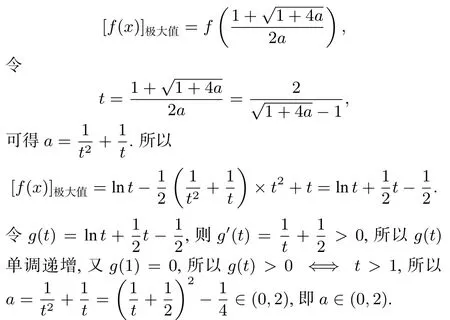
點評本題也是導數零點不可求題型,參考答案是用比較復雜的設而不求的思想方法解答的.實際上,本題的導函數的零點可用二次方程的求根公式直接求出,雖然表面上看起來很復雜,但通過發掘根與參數的關系,利用整體換元,并限定出t的范圍,可構造一個較為簡單的函數解決,反而有四兩撥千斤之妙!

例3已知函數.

(1)當a=-4時,試判斷函數f(x)在(-4,+∞)上的單調性;

(2)若函數f(x)在x=t處取到極小值.

①求實數t的取值集合T;

解析(1)略;(2)①略;②

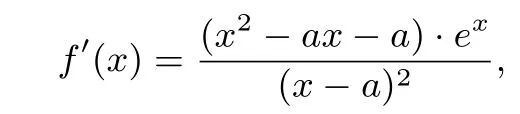
因為且函數f(x)在x=t處取到極小值,所以t2-at-a=0,且Δ=a2+4a＞0,結合a＜0,解得a＜-4.所以

點評本題與例1是類型題,但更為復雜,“暴力”求根的美感及精妙之處顯露無疑.筆者發現,求根公式在求解這類導數零點不可求問題時具有一定的通性通法.原來解題還有這樣的快感!

二、解析幾何中的應用

設而不求是解析幾何的最常用的技巧,其重要性不言而喻.在涉及直線與圓錐曲線的綜合解答題中,這種策略尤其顯得如魚得水.但是,反其道而行之,未嘗不可,設且求實際上也是一種有效的解決解析幾何問題的重要手段,有時會達到意想不到的效果.而這種方法普遍被大部分人所忽視.下面讓我們再次感受一下“暴力”求根法的威力.

例4已知焦點在x軸上的橢圓E:=1內含圓C:x2+y2=.圓C切線l與橢圓E交于A,B兩點,滿足.

(1)求b2的值;

(2)求|AB|的取值范圍.

解析： 依題意知直線OA,OB的斜率均存在,設A(xA,yA)為第一象限的點,直線OA的方程為y=kx,聯立.所以有xA=.令

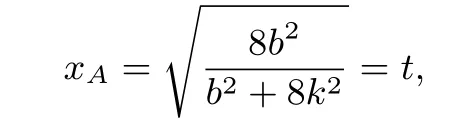
則yA=kt.設B(xB,yB).則

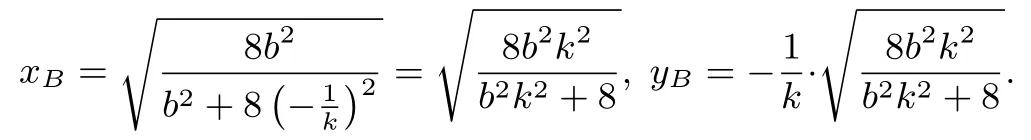
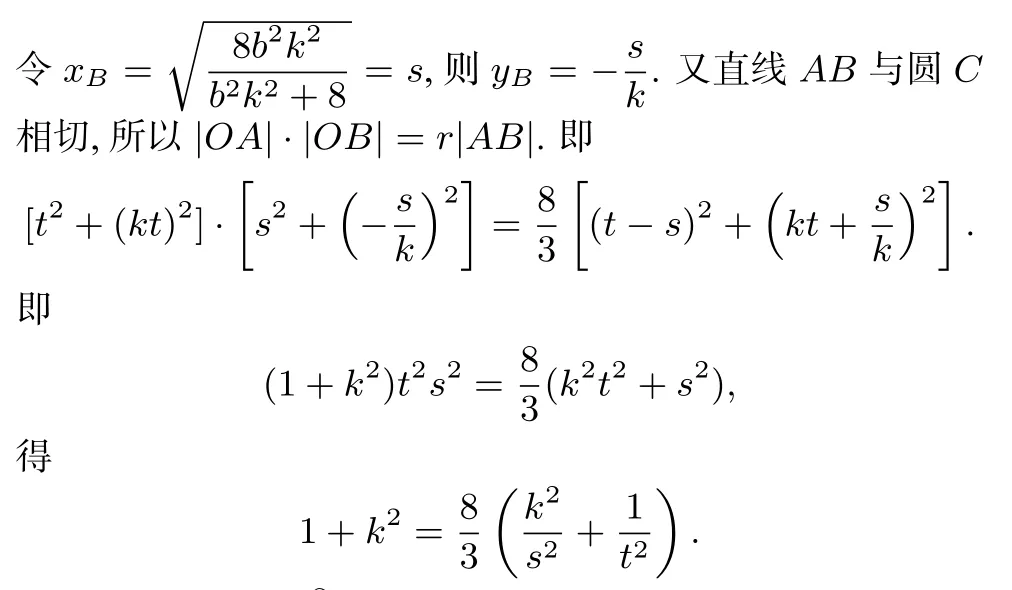
即8b2(1+k2)=(8+b2)(1+k2).因為1+k2/=0,所以8b2=(8+b2),即b2=4.易驗證當k不存在時,也滿足b2=4.點A在其它象限時,同理可解得b2=4.

(2)由(1)得

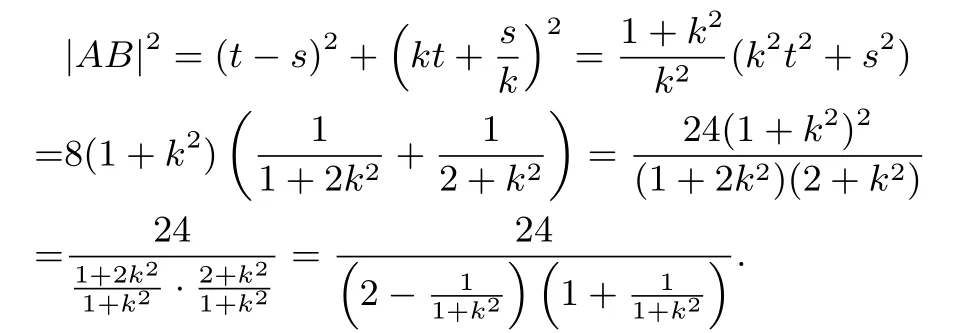
點評通過分析發現,直線與曲線的交點坐標并不難求,若能用設且求的思想,并以換元法為武器,可提高解題效率.筆者發現,這種設且求的思想被很多人忽視,被認為運算復雜,不利于問題的解決.這其實是值得商榷的.本題通過“暴力”求根,利用換元思想,運算并不復雜,甚至比用設而不求的方法簡單得多.這說明,若能走出思維的牢籠,則能實現方法的創新.

例5如圖,在平面直角坐標系 xOy中,橢圓=1(a＞b＞0)的右焦點F(1,0),離心率為.分別過O,F的兩條弦AB,CD相交于點E(異于A,C兩點),且 OE=EF.

圖1

(1)求橢圓的方程;

(2)求證：直線AC,BD的斜率之和為定值.

解析(1)略;

(2)由OE=EF可得∠EOF=∠EFO,所以直線AB與直線CD的斜率互為相反數,設AB的方程為y=kx,直線CD的方程為y=-k(x-1).聯立

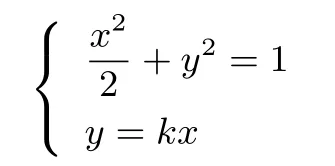
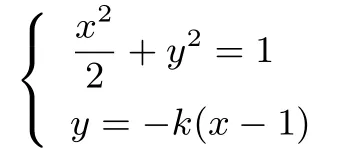
點評本題通過“暴力”求根,借助換元思想,完全走出了思維的牢籠,使我們再次見識了這種思想方法的威力!

通過以上的分析,我們認識到,對于有些問題,雖然已經有常見的通法存在,但鑒于其局限性與數學思想方法的多樣性,還可從其他角度解決問題.這說明,我們在研究問題時,不能固步自封,思維定勢,以致禁錮了自己的思維.若能打破固有的僵化思維,則能實現方法的創新.而這種創新思維則是我們最需要在教學過程中培養和傳授給學生的.而且這種創新的思維,對于提高教師教學的有效性具有不可估量的作用,而且對學生的成長與發展具有深遠的意義.