基于摩擦因素和風險價值的可能性組合投資模型

景永強，曹詠弘，李阿娜

(中北大學 理學院，太原 030051)

基于摩擦因素和風險價值的可能性組合投資模型

景永強，曹詠弘，李阿娜

(中北大學 理學院，太原 030051)

研究了在摩擦市場因素的條件下基于可能性分布理論的組合投資問題，提出了基于摩擦市場因素和風險價值理論的可能性組合投資模型。實證研究結果表明：摩擦市場因素的變動對組合投資風險具有一定的影響，基于摩擦市場因素和風險價值理論的可能性組合投資模型更符合實際的投資風險情況。本研究為投資者選擇更適合的投資策略提供參考。

可能性理論；摩擦因素；風險價值；組合投資

1952年馬克維茨提出了基于均值-方差的組合投資模型，對組合投資模型進行了定量的研究[1-2]。而使用均值與方差度量組合投資的收益和風險，只是通過方差來度量風險的波動情況，不能將波動的風險進行具體的定量化，因此學者們相繼提出了風險價值(VaR)模型及條件風險價值(CVaR)模型[3-4]。目前，大部分的組合投資模型研究是基于概率分布進行的，但在實際的投資市場存在很多不確定性的因素，通過概率分布研究得到的誤差較大，因此很多學者基于可能性分布研究金融市場的不確定性，提出了基于可能性分布理論的組合投資模型[5-15]。然而，國內外學者都是基于單一的影響因素研究可能性理論下的組合投資模型，并沒有考慮在綜合各個影響因素情形下的組合投資模型，而組合投資的收益受到系統風險和非系統風險的雙重影響，因此本文在已有文獻的基礎上，綜合考慮風險價值因素和摩擦市場因素，提出了一個在摩擦市場條件下的帶有風險價值約束的可能性組合投資模型。由于該模型中加入了摩擦市場因素和風險價值約束，可以更好地描述投資市場的環境和投資者的風險厭惡程度。最后通過選取股票市場的歷史數據進行實證分析，驗證了該模型的有效性，并且通過與不帶摩擦市場因素的模型相比較，表明市場摩擦因素對組合投資風險具有一定的影響。

1 可能性的定義及性質

1.1 可能性均值與方差的定義及性質

定義1[5]設A是一個模糊數，A的λ截集表示為Aλ=[a-(λ),a+(λ)]，則A的可能性均值可以表示為

A的可能性方差可表示為

定義2[5]如果A和B是兩個模糊數，其截集分別為Aλ=[a-(λ),a+(λ)]，Bλ=[b-(λ),b+(λ)]，則A和B的可能性協方差可以表示為

如果A和B表示兩個模糊數，k表示一個實數，則模糊數的均值滿足[6]：

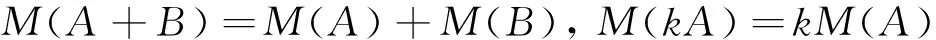
模糊數的方差滿足[6]：

1.2 可信性風險價值(VaR)的定義及性質

定義3[7]設A是一個具有隸屬函數μ(x)模糊數，t表示一個實數，S表示任意的實數集，則{A≤t}的可信性測度可表示為

其中：

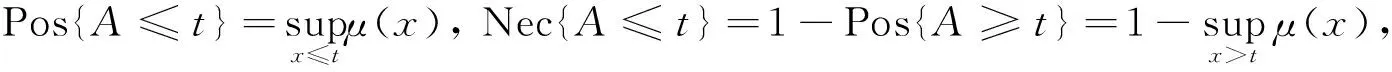
VaR(value at risk)即風險價值，表示投資者在給定置信水平b的情形下，在Δt的持有期內的投資組合的最大損失值。假定Δp表示在持有期內投資組合的價值改變量，則在概率測度的理論下，VaR的定義為[8]：

prob(Δp≤VaR)=1-b

通過概率測度下的VaR定義可推出在可信性測度的條件下VaR的定義，可表示為：

Cr(ΔA≤VaR)=1-b

其中：Cr表示可信性測度；b為置信水平；ΔA表示在持有期Δt內投資組合的價值改變量。

2 基于摩擦因素和風險價值的可能性組合投資模型

實際的金融市場中存在著很多市場摩擦因素，例如股票的紅利。投資者在進行股票資產投資時，會產生一定的成本費用，交易的過程中會產生印花稅及其他費用等，這些因素在投資決策中具有很大的影響作用。因此，針對風險厭惡性投資者，考慮基于摩擦因素和風險價值的可能性組合投資模型具有更實際的指導意義。

本文將證券市場中的紅利、稅收和資產的交易費用作為摩擦因素，在此情形下構建可能性組合投資模型。假設投資總資產為1，投資于n個風險資產，設ri為第i個資產的收益率，ri是一個模糊數，di表示第i種資產的紅利率，t1為資本收入稅率，t2表示基本收入稅率。采用絕對值型的交易費用函數，這樣投資的資產組合其總的交易費用可表示為

組合投資總的收益可表示為

則組合投資收益的可能性均值和方差可表示為：

因此，本文在基于風險價值的可能性組合投資模型的基礎上，通過綜合考慮市場中的摩擦因素，構建了基于摩擦因素和風險價值的可能性組合投資模型，可表示為：

其中：L表示期望收益率；b表示置信水平；c(x)表示交易費用函數；Cr表示可信性測度。基于風險價值的可能性組合投資模型可表示為：

基于摩擦因素和風險價值約束的可能性均值-方差模型，在給定收益率模糊變量的可能性分布情形下，可得到一個確定性的組合投資模型。假定資產的收益率ri是鐘形模糊數，則ri～B(μi,σi)，收益率ri的隸屬函數可表示為

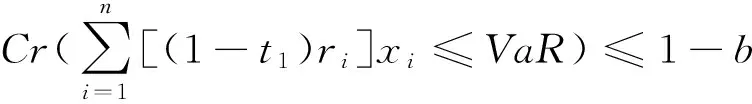
其中b>0.5。

在鐘形可能性分布下，組合投資收益的可能性均值和方差可表示為：

針對模型中的非光滑的交易費用函數，令

則交易費用函數可表示為

其中ui滿足

則在鐘形可能性分布情形下，基于摩擦因素和風險價值的可能性組合投資模型可表示為：

其中：L表示期望收益率；b表示置信水平；c(x)表示交易費用函數。該模型為非線性約束規劃模型，可通過Matlab中非線性約束優化方法進行模型的求解。

3 實證分析

對本文提出的在鐘形可能性分布情形下，基于摩擦因素和風險價值的可能性組合投資模型進行數值實驗和實證分析，并假設投資過程中不能賣空。由于投資者的風險厭惡性，所以在上證A股和深證A股市場中分別選取8只經營業績較好的股票進行實證研究，股票名稱及代碼為:國電南自(600268)、宏發股份(600885)、東方通信(600776)、華海藥業(600521)、江鈴汽車(000550)、國際實業(000159)、金科股份(000656)、山大華特(000915)。收集這8只股票從2011年1月1日—2015年12月31日的月平均收益率(數據來源于國泰安CSMAR數據庫),通過每種資產的歷史資產收益率的數據，計算每只股票的期望和標準差,如表1所示。

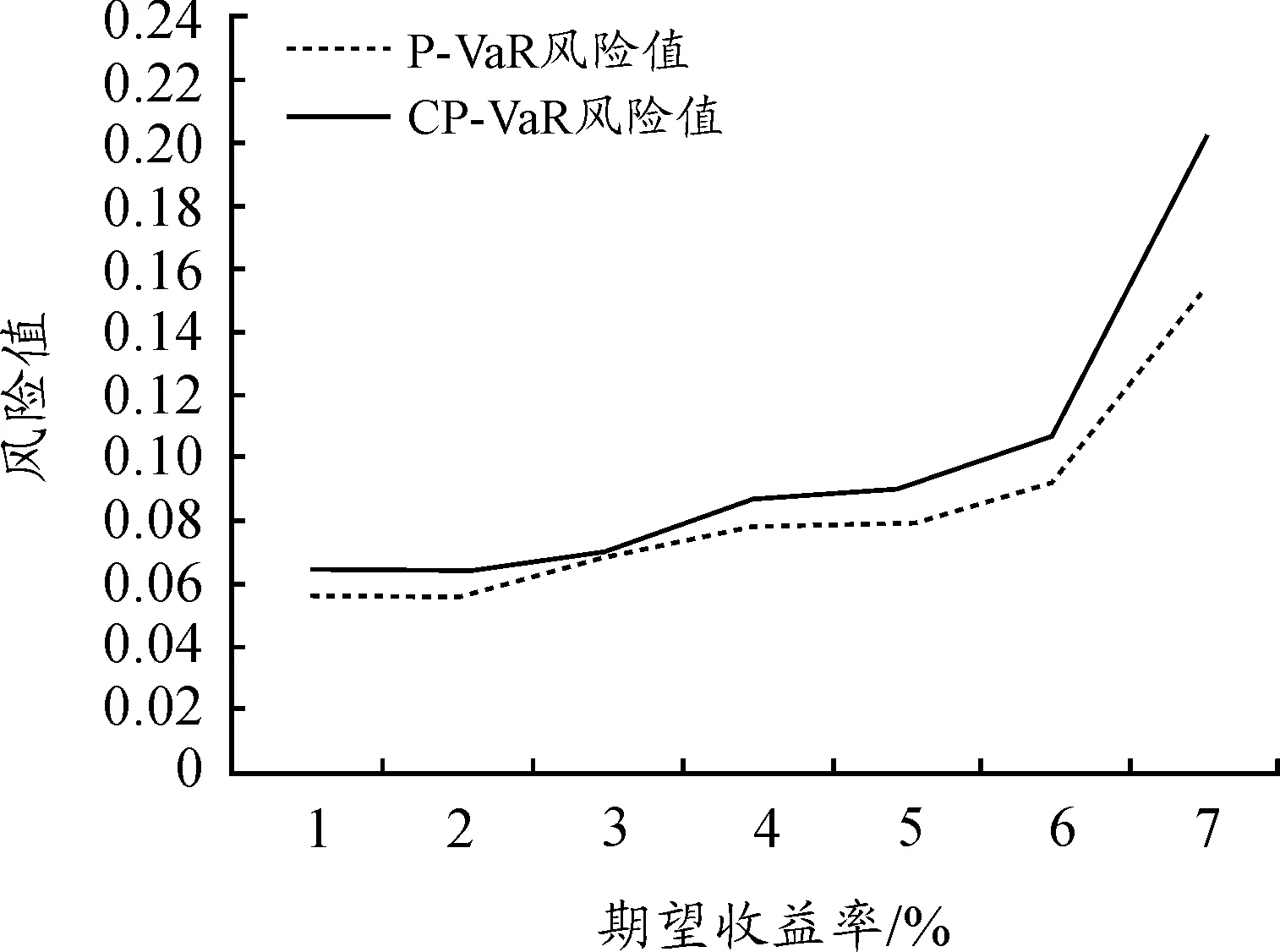
圖1 不同期望收益率下的組合投資風險值Fig.1 Portfolio risk value under different expected return

1)為了驗證模型的有效性和摩擦市場的因素對模型的影響，通過設定不同的預期收益率，在資產初始比例(0.125,0.125,0.125,0.125,0.125,0.125,0.125,0.125)，VaR為0.1，置信度為95%，交易費用比例為0.3%，紅利率為0.1%，稅率t1、t2分別為0.3%和0.2%的條件下，通過Matlab軟件分別對基于風險價值的可能性組合投資模型、基于摩擦因素和風險價值的可能性組合投資模型進行求解。 將基于風險價值的可能性組合投資模型、基于摩擦因素和風險價值的可能性組合投資模型分別記作P-VaR模型和CP-VaR模型，所得結果如表2和圖1所示。

表1 資產的期望與標準差

表2 不同期望收益率下的組合投資風險值

由表2和圖1可知：隨著投資者預期收益率的增大，投資組合的風險在不斷增大，符合收益越大、風險越大的市場規律，并且CP-VaR模型比P-VaR模型的風險值較大。由于摩擦因素的存在會降低組合投資的收益，導致組合投資的風險增加，因此具有較大風險的CP-VaR模型能夠提供更加符合實際的投資決策。

2)為了研究市場摩擦因素的變動對組合投資風險的影響，設定不同的交易費用比例。在資產初始比例為(0.125,0.125,0.125,0.125,0.125,0.125,0.125,0.125)，VaR為0.1，置信度為95%，預期收益率為6%，紅利率為0.1%，稅率t1和t2分別為0.3%和0.2%的條件下，通過Matlab軟件對基于摩擦因素和風險價值的可能性組合投資模型進行求解，所得結果如表3所示。

由表3可得:隨著資產交易費用比例的增大，組合投資的風險值在不斷增大。在期望收益率的約束下，當交易費用增加時，投資資產將配置于高風險的股票資產中，可提高組合投資的整體收益率，符合“高風險、高收益”的市場規律，驗證了該模型的有效性，表明了市場摩擦因素的變動對組合投資的風險具有一定的影響。而且該模型綜合考慮了摩擦市場因素和風險價值因素，投資者可根據自身投資的實際情況選擇合適的參數，得到最優的資產配置策略，因此基于摩擦因素和風險價值的可能性組合投資模型更加符合實際投資情況。

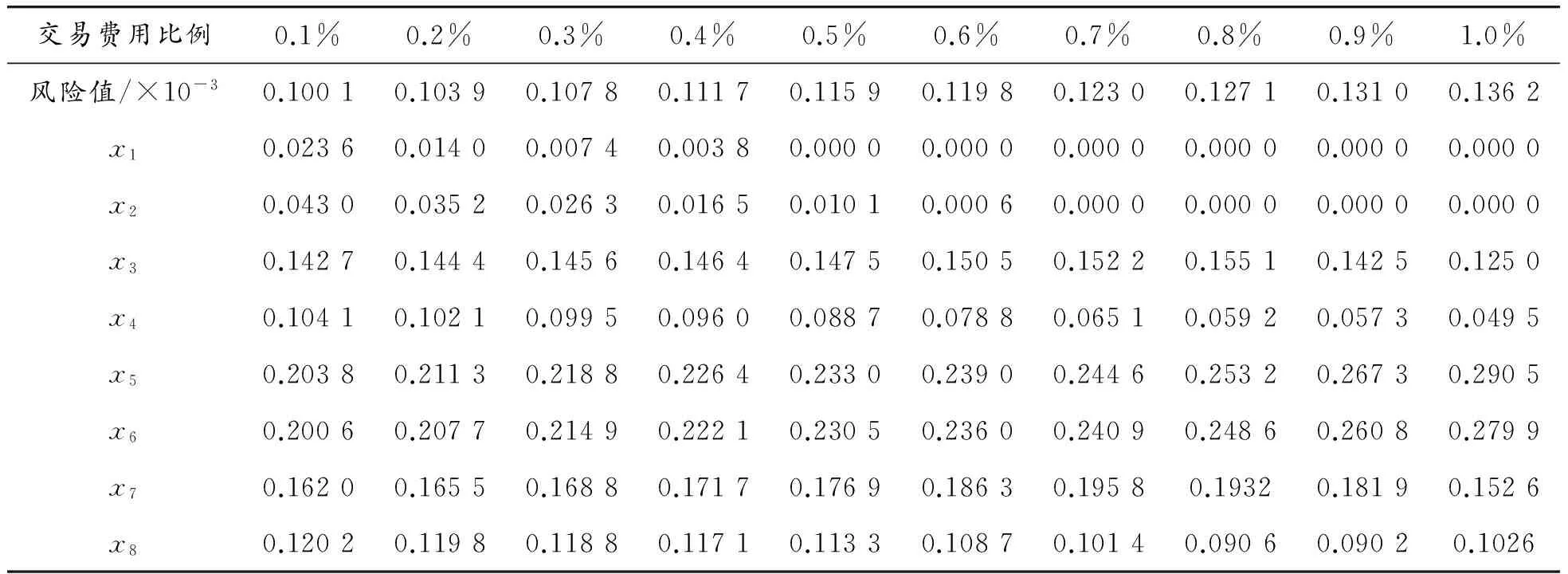
表3 不同交易費用比例下的組合投資風險值

4 結束語

本文研究了在摩擦市場因素的條件下基于可能性分布理論的組合投資問題。在可能性分布理論和風險價值的基礎上，提出了一個在摩擦市場條件下帶有風險價值約束的可能性組合投資模型。由于該模型中加入了摩擦市場因素和VaR約束，因此可以更好地描述投資市場的環境和投資者的風險厭惡程度。最后選取股票市場的歷史數據進行實證分析。實證研究結果表明，隨著投資者預期收益率的增大，投資組合的風險在不斷增大，符合“收益越大、風險越大”的市場規律。此外，在期望收益率一定的條件下,隨著資產交易費用的不斷增大，模型的目標值在逐漸變大，并且市場摩擦因素的變動對組合投資的風險具有一定的影響，基于摩擦市場因素和風險價值理論的可能性組合投資模型更符合實際的投資風險情況，可為投資者選擇更適合的投資策略提供參考。

[1] MARKOWITZ H.Portfolio selection[J].The Journal of Finance,1952,7(1):77-91.

[2] BASAK S,SHAPIRO A.Value-at-Risk-based risk management:Optimal policies and asset prices[J].The Review of Financial Studies,2001,14(2):371-405.

[3] ALEXANDER G J,BAPTISTA A M.Economic implications of using a mean-VaR model for portfolio selection:A comparison with mean-variance analysis[J].Journal of Economic Dynamics and Control,2002,26(7):1159-1193.

[4] ALEXANDER G J,BAPTISTA A M.A comparison of VaR and CVaR constraints on portfolio selection with the mean-variance model[J].Management Science,2004,50(9):1261-1273.

[5] ZHANG W G,XIAO W L,WANG Y L.A fuzzy portfolio selection method based on possibilistic mean and variance[J].Soft Computing,2009,13(6):627-633.

[6] BAPTISTA A M.Optimal delegated portfolio management with background risk[J].Journal of Banking & Finance,2008,32(6):977-985.

[7] JIANG C,MA Y,AN Y.An analysis of portfolio selection with background risk[J].Journal of Banking & Finance,2010,34(12):3055-3060.

[8] ZHANG W G,ZHANG X L,CHEN Y X.Portfolio adjusting optimization with added and Transaction costs based on credibility measures[J].Insurance:Mathematics and Economics,2011,49(3):353-360.

[9] ZHANG W G,XIAO W L,WANG Y L.A fuzzy portfolio selection method based on possibilistic mean and variance[J].Soft Computing,2009,13(6):627-633.

[10]李婷.考慮背景風險因素的可能性組合投資選擇模型研究[D].廣州： 華南理工大學,2013.

LI Ting.Study on portfolio selection model based on the possibility of background risk[D].Guangzhou:South China University of Technology,2013.

[11]何莎,周樹民.摩擦市場下基于可能性理論的一種組合投資模型[J].江漢大學學報(自然科學版),2009,37(4):16-18.

HE Sha,ZHOU Shumin.A portfolio investment model based on possibility theory in friction market[J].Journal of Jianghan University (Natural Science Edition),2009,37(4):16-18.

[12]何莎.摩擦市場下基于可能性理論的組合投資模型研究[D].武漢:武漢理工大學,2009.

HE Sha.Research on portfolio investment model based on possibility theory in friction market[D].Wuhan:Wuhan University of Technology,2009.

[13]喬峰,黃培清,顧鋒.可能性組合投資模型[J].上海交通大學學報,2005,39(10):1606-1610.

QIAO Feng,HUANG Peiqing,GU Feng.Portfolio selection model[J].Journal of Shanghai Jiao Tong University,2005,39(10):1606-1610.

[14]李婷.具有VaR約束的不相關資產可能性組合投資模型及算法[J].寧夏工程技術,2014,13(1):8-12.

LI Ting.The model and algorithm of portfolio investment with VaR constraints based on probability[J].Ningxia Engineering and Technology,2014,13(1):8-12.

[15]付云鵬,馬樹才,宋琪.基于可能性均值方差模型的社保基金組合投資研究[J].經濟與管理評論,2013(3):111-114.

FU Yunpeng,MA Shucai,SONG Qi.Study on portfolio investment of social security funds based on the model of possible mean variance[J].Review of Economics and Management,2013(3):111-114.

(責任編輯 劉 舸)

Research on the Possibility of Portfolio Investment Model Based on Friction Factor and Value at Risk

JING Yong-qiang, CAO Yong-hong, LI A-na

(School of Science, North University of China, Taiyuan 030051, China)

The portfolio investment based on the possibility distribution theory under the condition of the friction market was studied, and a possibility portfolio investment model was proposed. The empirical study shows that the change of the market friction factor affects the investment portfolio. Thus, the portfolio investment model based on the friction market factor and the VaR theory is more suitable for the actual investment risk, so as to provide a reference for the investor to choose a more suitable investment strategy.

possibility theory; friction factor; value at risk; portfolio investment

2016-10-25 基金項目：電子測試技術國家重點實驗室基金資助項目(9140C120401080C12)；中北大學科學基金資助項目(201406)

景永強(1993—)男，山西臨汾人，碩士研究生，主要從事可能性理論的應用研究，E-mail:474060802@qq.com; 曹詠弘(1972—)男，山西太原人，副教授，碩士生導師,主要從事工程中的數學問題研究。

景永強，曹詠弘，李阿娜.基于摩擦因素和風險價值的可能性組合投資模型[J].重慶理工大學學報(自然科學)，2017(3):158-164.

format：JING Yong-qiang, CAO Yong-hong，LI A-na.Research on the Possibility of Portfolio Investment Model Based on Friction Factor and Value at Risk[J].Journal of Chongqing University of Technology(Natural Science)，2017(3):158-164.

10.3969/j.issn.1674-8425(z).2017.03.024

O21；F830

A

1674-8425(2017)03-0158-07