淺析原子堆積中的空隙問題

衛(wèi)卓凡

高中化學(xué)選修三物質(zhì)結(jié)構(gòu)與性質(zhì)中有一類關(guān)于原子的最密堆積試題中經(jīng)常會考查微粒之間的距離以及微粒之間的空隙大小等問題，這是在晶體結(jié)構(gòu)中相對比較復(fù)雜的一類計(jì)算，因?yàn)樯婕暗娇臻g想象能力和數(shù)學(xué)運(yùn)算能力的考查，有些同學(xué)遇到此類問題往往無從下手。有的同學(xué)雖然也能解出結(jié)果，但并不是很清楚這晶體中的微粒之間的分布規(guī)律和對應(yīng)的位置關(guān)系，因此不能做到舉一反三。

原子堆積空隙等徑球最密堆積中的空隙分兩種：

（1）四面體空隙：由四個(gè)球體圍成的空隙，球體中心線圍成四面體；

（2）八面體空隙：由六個(gè)球圍成的空隙，球體中心線圍成八面體形。

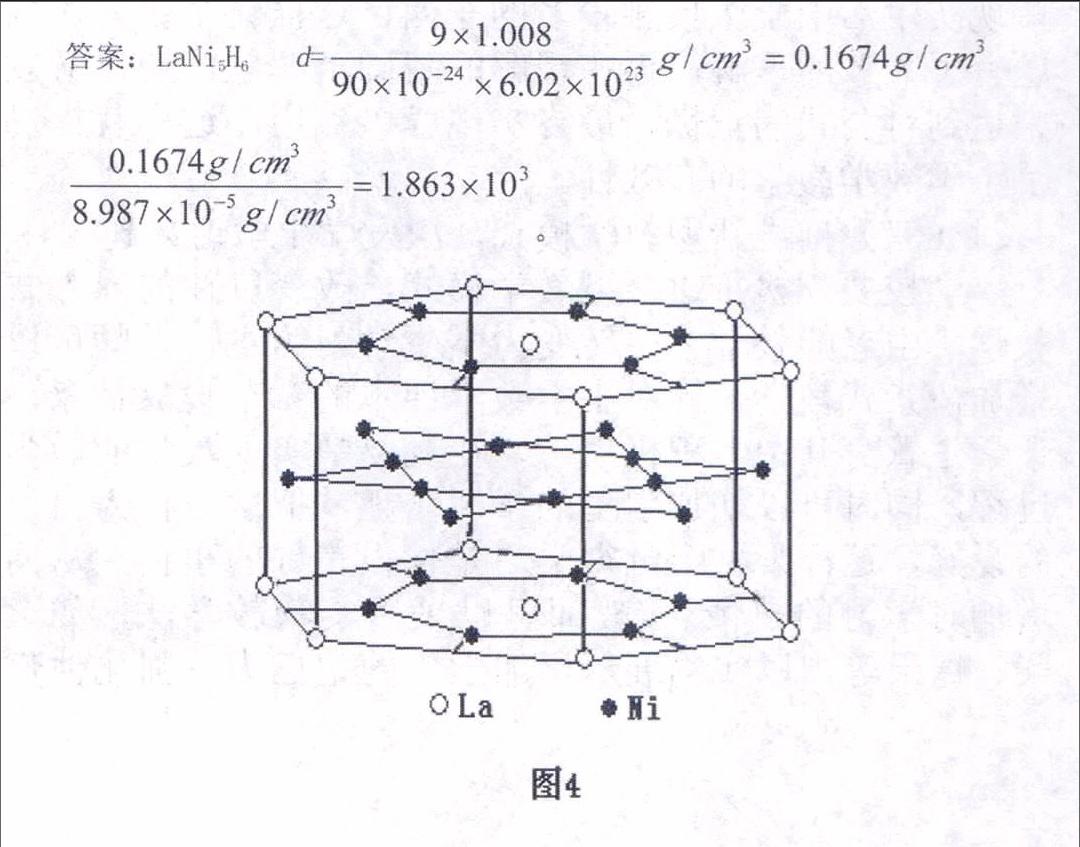
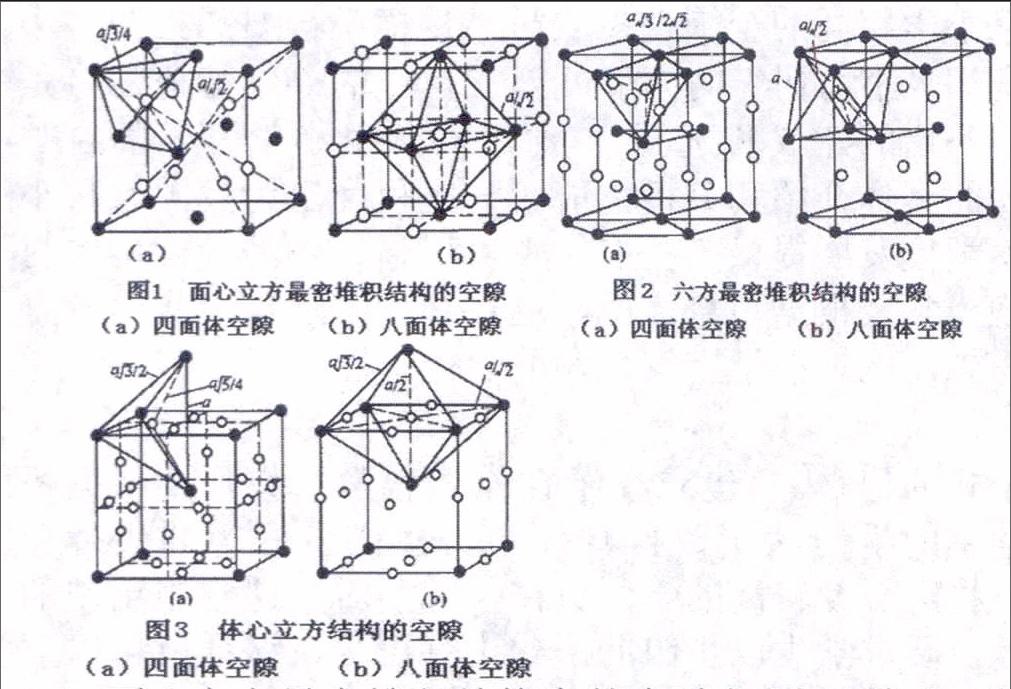
面心立方最密堆積結(jié)構(gòu)中的空隙如圖1所示，六方最密堆積結(jié)構(gòu)的空隙如圖2所示，體心立方堆積結(jié)構(gòu)的空隙如圖3所示。

以金屬Cu晶胞為例，來說明面心立方緊密堆積中的八面體和四面體空隙的位置和數(shù)量：

以Cu晶胞中上面心的一個(gè)球?yàn)檠芯繉ο螅恼路接?個(gè)八面體空隙（體心位置）。與其對稱，正上方也有1個(gè)八面體空隙；前后左右各有1個(gè)八面體空隙（棱心位置）。所以一個(gè)球共參與形成了6個(gè)八面體空隙，由于每個(gè)八面體空隙由6個(gè)球構(gòu)成，所以屬于這個(gè)球的八面體空隙數(shù)為6×1/6=1。

在這個(gè)晶胞中，上面心這個(gè)球還與另外兩個(gè)相鄰面面心處的2個(gè)球及頂角上的1個(gè)球，共能構(gòu)成4個(gè)四面體空隙（即1/8小立方體的體心位置）；由于對稱性，在上面的晶胞中，也有4個(gè)四面體空隙由這個(gè)球參與構(gòu)成。……