基于無網格方法的圓柱型催化劑體相溫度分布數值模擬

王 闊

(中國石化 撫順石油化工研究院， 遼寧 撫順 113001)

基于無網格方法的圓柱型催化劑體相溫度分布數值模擬

王 闊

(中國石化 撫順石油化工研究院， 遼寧 撫順 113001)

以真實圓柱型加氫裂化催化劑三維體相環境為計算實體，以模擬工業運行溫度的定值函數作為邊界條件，采用無網格數值方法求解傅里葉傳熱方程，并使用計算結果分析加氫裂化催化反應過程中外界溫度對于催化劑內部溫度分布的影響。結果表明，實際加氫裂化反應過程中，催化劑顆粒內部并非等溫，外界的反應溫度以及催化劑顆粒內部的熱點分布對于催化劑團簇內部的溫度場分布有一定的影響。催化劑體相內部的平均溫度也隨著反應體系放熱情況、催化劑粒徑、原料油密度、反應空速以及催化劑內部熱點分布情況的不同而有所變化。

加氫裂化； 傳熱； 無網格； 數值模擬； 分布計算

一般來講，加氫裂化反應是一種整體具有強烈放熱效應的反應，溫度和熱量是該類反應最重要的影響因素。對于加氫裂化反應體系的能量恒算以及節能研究眾多[1-2]，但一般僅限于較大空間尺度或單純反應熱層面[1-3]。在科學實驗和工業生產實踐中，對于小型實驗裝置而言，整個反應系統基本可以近似視為等溫反應系統；對工業裝置而言，反應系統可以被視為一個比較嚴格的絕熱系統。在反應過程中，反應器內部的溫度分布必然會影響到催化劑床層不同位置的反應速率，進而影響到相關位置的熱量釋放。對于反應系統尤其是與工業裝置緊密相關的絕熱系統而言，反應產生熱量的傳遞必然引起體系溫度分布的重新調整。這一溫度的正反饋過程在加氫裂化工業生產中十分重要。

審視整個加氫裂化溫度正反饋過程不難發現，在絕熱反應體系中，整個過程的熱量正是來自于催化劑顆粒自身，每個催化劑顆粒都相當于反應體系的1個“微熱源”。這些微熱源的溫度分布情況直接或間接的影響到反應體系的質量傳遞、熱量傳遞和反應進程以及產品分布，催化劑體相內部的溫度分布對于催化劑的壽命也有著極大的影響。因此，對于催化劑內部體相溫度分布的描述意義十分重大。

對于催化劑內部體相溫度分布的研究十分困難。傳統的煉化工業一般采用熱電偶測定溫度，但只能測定得到反應器內部的宏觀點的溫度近似值，無法分析反應過程的實時微觀熱效應。雖然近年來“非接觸式”的紅外測溫技術得到廣泛發展[4]，但由于催化劑內部微小而復雜的形態結構，還沒有任何溫度測量設備能夠在如此微觀尺度進行溫度測量；同時，由于催化劑外觀幾何形態以及反應溫度條件的復雜性，導致常規導熱模型體系的經驗公式難于適用。因此，基于傅里葉傳熱定律的數值模擬方法成為解決這一類問題的有效途徑。

1 圓柱型催化劑體相溫度分布數值模擬理論及計算部分

1.1 傅里葉傳熱方程簡介

對于一般的傳熱過程，當存在穩定熱源時，其溫度對于空間的分布形態可由1個泊松型的穩態傅里葉傳熱方程確立。對于1個三維體系，其一般的數學形式如式(1)所示。

(1)

在式(1)中，F(x,y,z)為體系內溫度對于空間的函數，當空間點處于體相內部ν時，整個體系由1個泊松型的偏微分方程描述；qv(x,y,z)為體系的熱源函數，該函數表達當體系存在熱源或熱匯時，該熱源或熱匯對于空間的分布形式；λ為計算體系的導熱系數，由該體系組成材料的物化性質決定。當溫度點處于體相表面σ時，其溫度可以第1型迪里克萊邊界條件描述，也即可將其表面溫度分布表達為函數G(x,y,z)。對于極少數具有比較簡單的熱源或熱匯函數形式以及比較規則的幾何外觀形態和相對簡單的邊界條件的導熱體系，函數F(x,y,z)存在解析形式，同時拉普拉斯型方程的初值問題的解不穩定[13]。對于絕大多數較為復雜的實際工程傳熱體系，對相關模型方程體系的適定性問題討論極為復雜，因此，式(1)只能由數值方法進行求解。

1.2 加氫反應過程熱量衡算及相關方程參數確立

在一般的加氫裂化反應過程中，催化劑體系內部的溫度分布可由三維的傅里葉傳熱方程描述。但實際工業反應條件下的熱源函數以及催化劑表面溫度分布十分復雜，因此，對三維的傅里葉傳熱方程采用無網格數值方法進行求解。

一般而言，整個加氫裂化過程的精確反應熱計算比較困難，根據已有經驗及相關文獻，加氫裂化反應放熱范圍一般為200～500 J/g之間，而原料油密度一般在0.85～1.05 kg/L之間，反應過程的體積空速一般在0.9～1.5 h-1之間。通過這些數據，可對反應體系進行熱量衡算及相關方程參數估計。

例如，假定反應放熱Qm=500 J/g，油品密度ρ=1.05 kg/L，每加工1 L油品放熱量q=Qm·ρ=500 J/g×1.05 kg/L=525 kJ/L。假定相關反應空速LHSV=1.5 h-1，則每升催化劑每小時放熱Qv=q·LHSV=525 kJ/L×1.5 h-1=787.5 kJ/(L·h)，也即其單位體積熱功W=787.5 kJ/(L·h)=218.75 W/L=2.1875×10-4W/mm3。而一般催化劑的導熱系數λ在0.25～0.32 W/(m·K)范圍[10]。在此取導熱系數為2.58×10-4W/(mm·K)，因此，式(1)中相關熱功率與導熱系數的比值qv(x,y,z)/λ=(2.1875×10-4W/mm3)/(2.58×10-4W/(mm·K))= 0.85 K/mm2。

1.3 無網格方法簡介及計算過程介紹

較為復雜的工程偏微分方程目前主要采用數值方法進行求解，常規的數值方法包括有限差分方法(FDM)和有限元方法(FEM)。

FDM應用最早，但其對于復雜邊界條件的適應性很差。因此，在現代工程計算應用中受到了一定的限制。而FEM自20世紀50年代開始興起，堪稱數值方法領域的一個里程碑。該方法的主導思想是將1個復雜形態的連續體劃分成有限個單元，各個單元通過一定的規則連接起來。正是基于這一指導思想，使得FEM在處理復雜幾何形體的各種線性和非線性問題中表現出很強的靈活性和魯棒性，在工程領域得到廣泛應用，同時出現了大量的商業軟件包。

然而FEM也有其固有的缺點和局限性，例如有限元計算需要在計算前對計算體系進行相關的網格劃分。而形成相關計算網格計算成本比較高，特別是對于復雜的三維體系而言，生成復雜的高質量三維網格相當困難[11]。產生這類問題的根源在于在有限元計算過程中使用了生成網格單元的相關連接信息。形成一種不使用單元與網格劃分的方法十分重要，因此，近年來無網格類計算方法應運而生[14-16]。

在本研究中，嘗試使用無網格計算方法對三維傅里葉傳熱方程進行數值求解，進而實現對于具有不同熱點分布形態的圓柱型催化劑體相溫度空間分布形式的描述和分析。以下介紹整個計算的大略求解過程。

首先，對于指定采樣點確定相關的三維長方體計算支持域。在支持域中選擇具有局域性質的局域函數，該局域函數用多項式函數為基，相關基底函數L可以表示為三維二次基底函數集合如式(2)所示。其基底函數對應的矩陣規模為1×n。在計算過程中，首先計算在支持域內的計算點局域矩陣PT，如式(3)所示。

L={1,x,xy,xz,y,yz,z,x2,y2,z2}

(2)

(3)

式(3)中，PT的規模為m×n。m代表相關采樣點計算支持域內所包含的計算點數目，n則代表選定的三維二次基底函數的項數，在本研究中為10。

其次，選擇在相關的三維長方體計算支持域中的3次樣條權重函數ωx(Rx)，如式(4)所示。式(4)中的Rx由式(5)計算。

(4)

(5)

在式(5)中，xi為在支持域中的每個計算點的x軸坐標，而x為采樣點的x軸坐標；Rω，x為定義的權函數支持域在x軸方向的尺寸。在支持域外部的計算點權重值定義為0。

按此規則定義函數ωy(Ry)以及ωy(Ry)，最終定義權函數如式(6)所示。

ω(x-xi,y-yi,z-zi)=ωx(Rx)ωy(Ry)ωz(Rz)

(6)

按照式(6)在支持域內構造權重矩陣Ω， 如式(7)所示。

(7)

式(7)中，Ω的規模為m×m。m代表相關采樣點計算支持域所包含的計算點數目。

依據已定義的局域矩陣PT以及權函數矩陣Ω分別形成兩類矩陣A及B，如式(8)、(9)所示。

A=PΩPT

(8)

B=PΩ

(9)

式(8)、(9)中，A的規模為n×n；B的規模為n×m。

接下來，定義后續無網格計算使用的任意采樣點的形函數矩陣如式(10)所示。

Φ=LA-1B

(10)

依據相關定義，形函數矩陣規模為1×m，形函數本身是采樣點位置坐標的函數。

最后確立式(1)中函數F(x,y,z)近似表達式的具體形式為式(11)。

(11)

由于函數F(x,y,z)近似表達式中形函數為包含位置采樣點變量x，y以及z的函數，可將生成的形函數分別對x，y以及z進行偏導求取，其結果如式(12)～(14)所示。

(12)

(13)

(14)

將原函數式(11)及求導結果式(12)～(14)依次以相關矩陣的形式代入式(1)中的控制方程及邊界條件方程，經過整理獲得以計算點溫度數值為未知向量的線性方程組。對應線性方程組的系數矩陣及常數項矢量分別稱為 “力矩陣”和“載荷矩陣”。在“載荷矩陣”中可以根據具體的控制方程及邊界條件加載相關數據；根據計算需要，相關的“力矩陣”行數與列數，即采樣點個數與計算點個數可以相同也可以不同，采樣點位置與計算點位置可以重合也可以不重合，這也是無網格方法的靈活性之一。

最后，用線性最小二乘法求解力矩陣對于載荷矩陣的未知向量，即得到計算點溫度函數的近似數值。再用計算點溫度函數的數值與生成的形函數矩陣重構整個采樣點溫度函數數值，即可獲得原偏微分方程體系的近似數值解。

1.4 計算參數及邊界條件的設定

由于圓柱型催化劑幾何實體形狀的對稱性比較好，在計算過程中，將直角坐標系映射為柱坐標系。分別在柱體的半徑方向取6個徑向采樣點、徑向截面角方向取20個采樣點、在軸向方向取41個采樣點，同時生成5個徑向計算點、由于圓柱型催化劑幾何實體形狀的對稱性比較好，在計算過程中，將直角坐標系映射為柱坐標系。分別在柱體的半徑方向取6個徑向采樣點、徑向截面角方向取20個采樣點、在軸向方向取41個采樣點，同時生成5個徑向計算點、20個徑向截面角方向計算點和40個軸向計算點，其空間分布如圖1所示。在整個計算過程中，定義的權函數支持域尺寸為2。

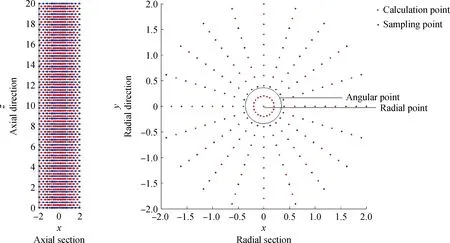
圖1 圓柱體采樣點及計算點分布Fig.1 Distribution of sampling and calculation points about cylinder

在催化劑工作過程中，催化劑內部溫度較其鄰域更高的區域稱為“熱點”。實際催化劑內部熱點的成因及分布十分復雜！由于實際催化劑制備過程及催化反應的極端復雜性，一般不能保證催化劑完全浸漬均勻；有時因特定的反應，甚至需要專門制備活性組分為蛋黃型或蛋殼型分布的非均勻催化劑[12]。也就是說，催化劑圓柱體內部很可能出現活性組分分布不均勻的現象，該現象導致了催化劑內部熱點分布不均勻，或出現突出熱點的情況。因此，相關的數值模擬應盡量考慮到實際工業催化劑的對應情況。為簡化問題，在整個計算過程中模擬了熱點均勻分布、熱點蛋黃型分布以及熱點蛋殼型分布3類不同類型的催化劑的溫度分布情況。

3類模擬計算均假定催化劑外部溫度為恒溫370℃。同時確保整個催化劑圓柱型顆粒的放熱功率與混合均勻情況下的放熱功率一致，但不同熱點分布形式對應的催化劑熱點的功率強度和位置則發生變化。也即調整相關參數使得式(15)保持不變。

(15)

在整個計算過程中，假定圓柱型催化劑長度為20 mm，半徑為2 mm，功率值W為0.1202 W。

第1類情況假定，催化劑內部熱點完全均勻，催化劑熱功率空間分布形式對于每種反應工況為定值，但隨具體反應工況的不同而有所變化。其相關催化劑體系溫度分布計算序號為1-16。

第2類情況假定，催化劑內只有1個蛋黃型分布的熱點區域。且熱點位置不發生變化，催化劑熱功率空間分布形式由式(16)描述。在計算過程中，調整相關參數C、D使得式(15)成立。所選3種條件對應計算序號及相關參數列于表1，相關熱功率函數圖像如圖2所示。

qv(x,y,z)=Ce(-D((x-x1)2+(y-y1)2))

(16)

第3類情況假定，催化劑內部熱點分布呈蛋殼型，且最高熱點位置發生變化，催化劑熱功率空間分布形式由式(17)描述。

qv(x,y,z)=A1e(-B1((x-x1)2+(y-y1)2))-
A1e(-B2((x-x1)2+(y-y1)2))

(17)

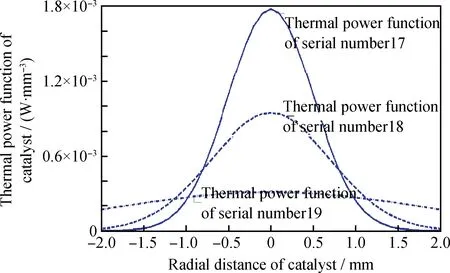
圖2 熱點蛋黃型分布的催化劑的熱功率函數Fig.2 Power function of the catalyst with hotspots eggyolk distribution

同樣在計算過程中調整相關參數A1、B1及B2使得式(15)成立，所選3種條件對應計算序號及相關參數列于表2，相關熱功率函數圖像如圖3所示。

表1 熱點蛋黃型分布的催化劑相關功率函數的計算參數Table 1 Calculation parameters of power function about the catalyst with hot spots eggyolk distribution

表2 熱點蛋殼型分布的催化劑相關功率函數的計算參數Table 2 Calculation parameters of power function about the catalyst with hot spots eggshell distribution

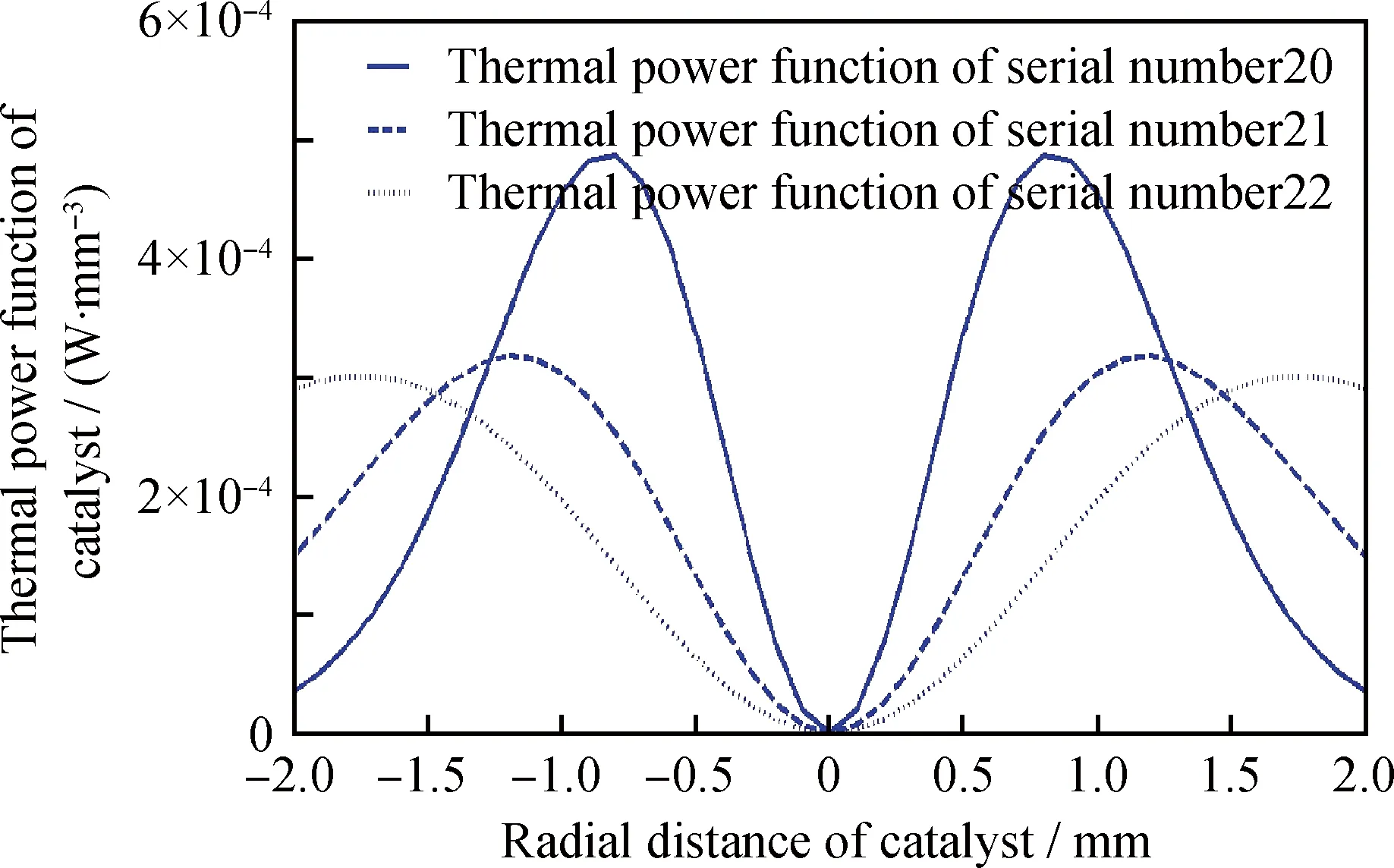
圖3 熱點蛋殼型分布的催化劑的熱功率函數Fig.3 Power function of the catalyst with hotspots egg shell distribution

1.5 模型所涉及的計算體系

整個計算過程使用的是分布式的高密度計算系統。其整套設備包含常規處理器計算機5臺，共計16整個計算過程使用的是分布式的高密度計算系統。其整套設備包含常規處理器計算機5臺，共計160核心。整個計算集群包含顯示體系和計算體系。顯示體系通過KVM切換器有遠程主機控制顯示。計算體系則有24口交換機完成計算數據的傳輸和交互。計算體系的每個計算點可以單獨并行使用，也可以整體分布使用。該系統十分適合高密度計算占優的系統體系。整個計算過程采用并行計算方式進行，形函數及其偏導數計算以及力矩陣及載荷矩陣的組裝過程采用多機并行計算，共有體系的160核心并行參與。

2 結果與討論

2.1 相關計算結果

對總計22種不同的工況條件進行計算，并對其中7種情況的三維溫度分布分別作二維切面圖和三維等勢圖。

2.2 等溫反應條件下熱點均勻型催化劑內部溫度場分析

計算了不同反應工況及催化劑尺度條件下熱點分布均勻的催化劑在外表面370℃進行反應時的催化劑內部溫度分布情況，將計算所得催化劑體系內部的最高溫度、平均溫度以及溫度分布的標準差列于表3。將7號計算對應的三維溫度場分布作二維軸向及徑向切面圖，結果示于圖4。

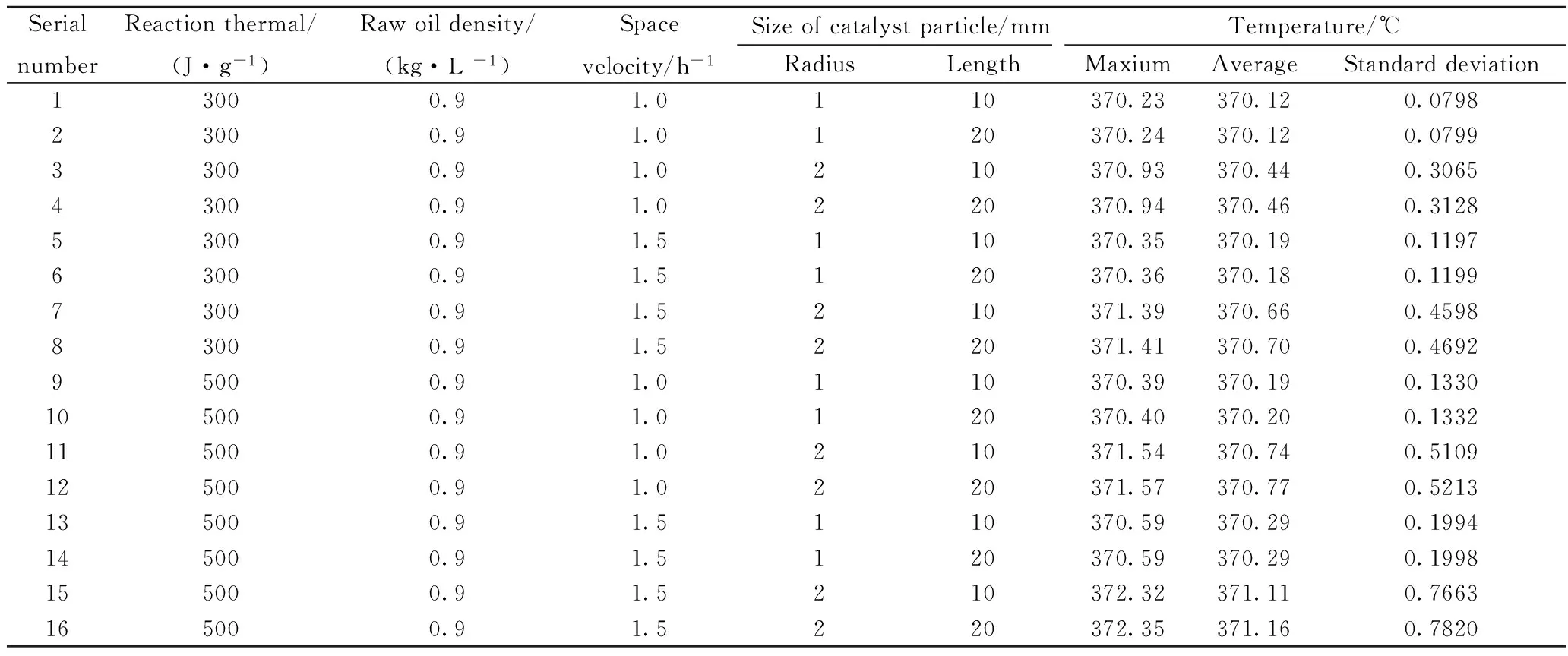
表3 熱點分布均勻的圓柱型催化劑表面370℃反應條件下的體相溫度性質Table 3 Bulk phase temperature properties of the cylindrical catalyst with hot spots homogeneousdistribution and uniform temperature of 370℃ on surface

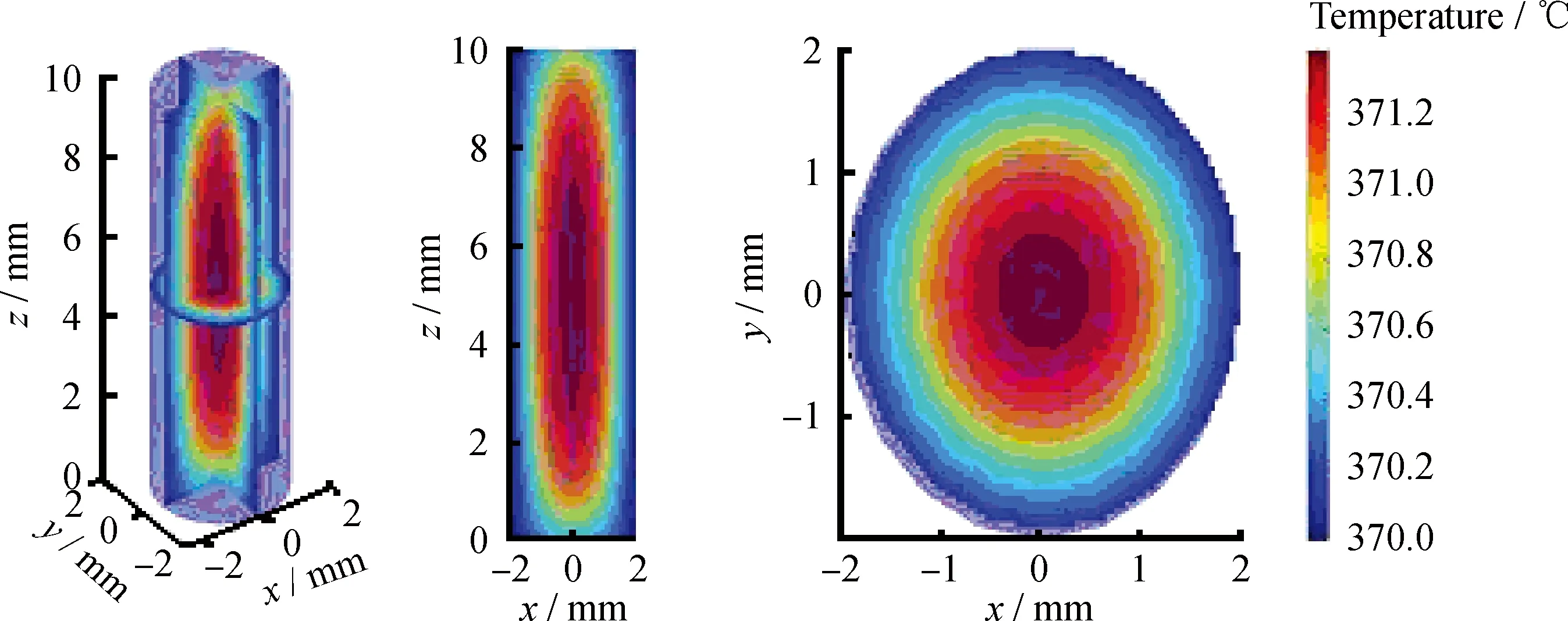
圖4 序號7條件催化劑內部溫度分布切片圖Fig.4 The internal temperature distribution of the catalyst in the serial number 7

對表3的分析發現，相關裂化反應的反應熱、原料油密度、反應空速以及催化劑半徑均直接或間接地影響催化劑內部的溫度分布，且所對應的相關不同工藝條件下催化劑內部的溫度分布比較相似。僅就單因素分析來看，催化劑顆粒內部最高溫度及平均溫度均隨反應熱、原料油密度、反應空速以及催化劑半徑和催化劑的軸向長度的增加而增大；就其影響效果而言，反應熱及催化劑顆粒半徑對于催化劑最高溫度及平均溫度的影響要顯著的大于催化劑顆粒長度、反應空速及原料油密度的影響。

對于熱點分布均勻的等溫反應條件，雖然不同計算工況對應的最高溫度及平均溫度數值有所不同，但其溫度分布形式基本類似。可以認為，溫度分布的等勢面在徑向方向是嚴格的圓型分布，而在軸向剖面上比較近似橢圓分布；在催化劑的外表面溫度為370℃時，催化劑內部溫度沿徑向和軸向逐漸增加，且徑向方向溫度梯度大于軸向方向的，在圓柱型催化劑中心的溫度最高。可以認為，雖然在理論上催化劑內部并非等溫環境，但其內部的反應環境與等溫環境比較類似。但當催化劑顆粒半徑及長度較大時，催化劑圓柱體中心最高溫度與表面溫度則相差較大，在該催化劑內部的反應相對于等溫反應偏離較大。因此，僅就熱效應而言，制備圓柱型催化劑時，其顆粒半徑及長度一般不宜過大。

2.3 等溫條件下不同熱點分布催化劑內部溫度場分析

模擬計算獲得的熱點蛋黃型分布催化劑的溫度場信息及分布圖分別列于表4及圖5。

表4 熱點蛋黃型分布催化劑的體相系溫度信息Table 4 Bulk phase temperature properties of the cylindrical catalyst with hot spots eggyolk distribution

The uniform temperature of 370℃ on surface

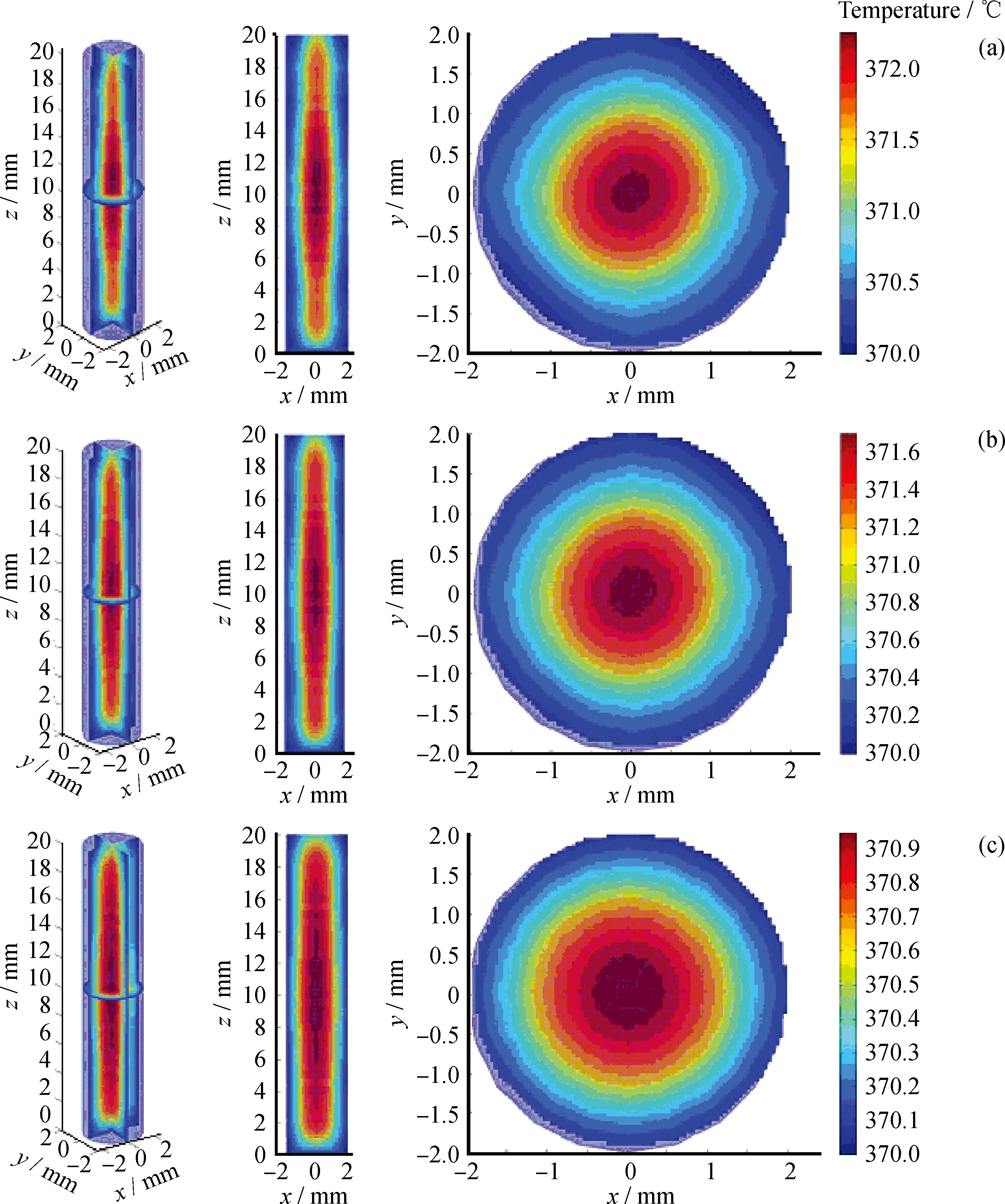
圖5 熱點蛋黃分布催化劑對應的體相溫度軸向及徑向分布圖Fig.5 The axial and radial temperature distribution of the catalyst with hot spots eggyolk distributionSerical number: (a) 17; (b) 18; (c) 19

從表4及圖5可以發現，第17～19號計算條件所對應蛋黃型催化劑熱點分布由集中逐步過渡到分散，所對應的熱功率空間分布形式逐漸呈均勻分布，第19號計算條件所對應熱功率已接近完全均勻分布；催化劑體系對應的最高溫度及平均溫度都逐漸降低，最終接近熱點均勻的催化劑體系；催化劑內部的軸向及徑向溫度分布的梯度逐漸降低，表征催化劑內部溫度波動的標準差逐漸減小，催化劑內部更接近等溫環境。

將模擬計算獲得的熱點蛋殼型分布的催化劑的溫度場信息及分布圖分別列于表5及圖6。

從表5及圖6可以發現，第20～22號計算條件所對應蛋殼型催化劑熱點分布由催化劑徑向中心逐步過渡到徑向邊緣，同時相關的熱功率函數峰值也有所降低；隨之催化劑體系對應的最高溫度及平均溫度都逐漸降低，最終甚至低于熱點均勻的催化劑體系；同時，催化劑內部的軸向及徑向溫度分布的梯度逐漸降低，催化劑內部接近等溫的區域逐漸增加，表征催化劑內部溫度波動的標準差逐漸減小，催化劑內部較蛋黃分布催化劑更接近等溫環境。

表5 熱點蛋殼型分布催化劑的體相溫度信息Table 5 Bulk phase temperature properties of the cylindrical catalyst with hot spots eggshell distribution

Uniform temperature of 370℃ on surface

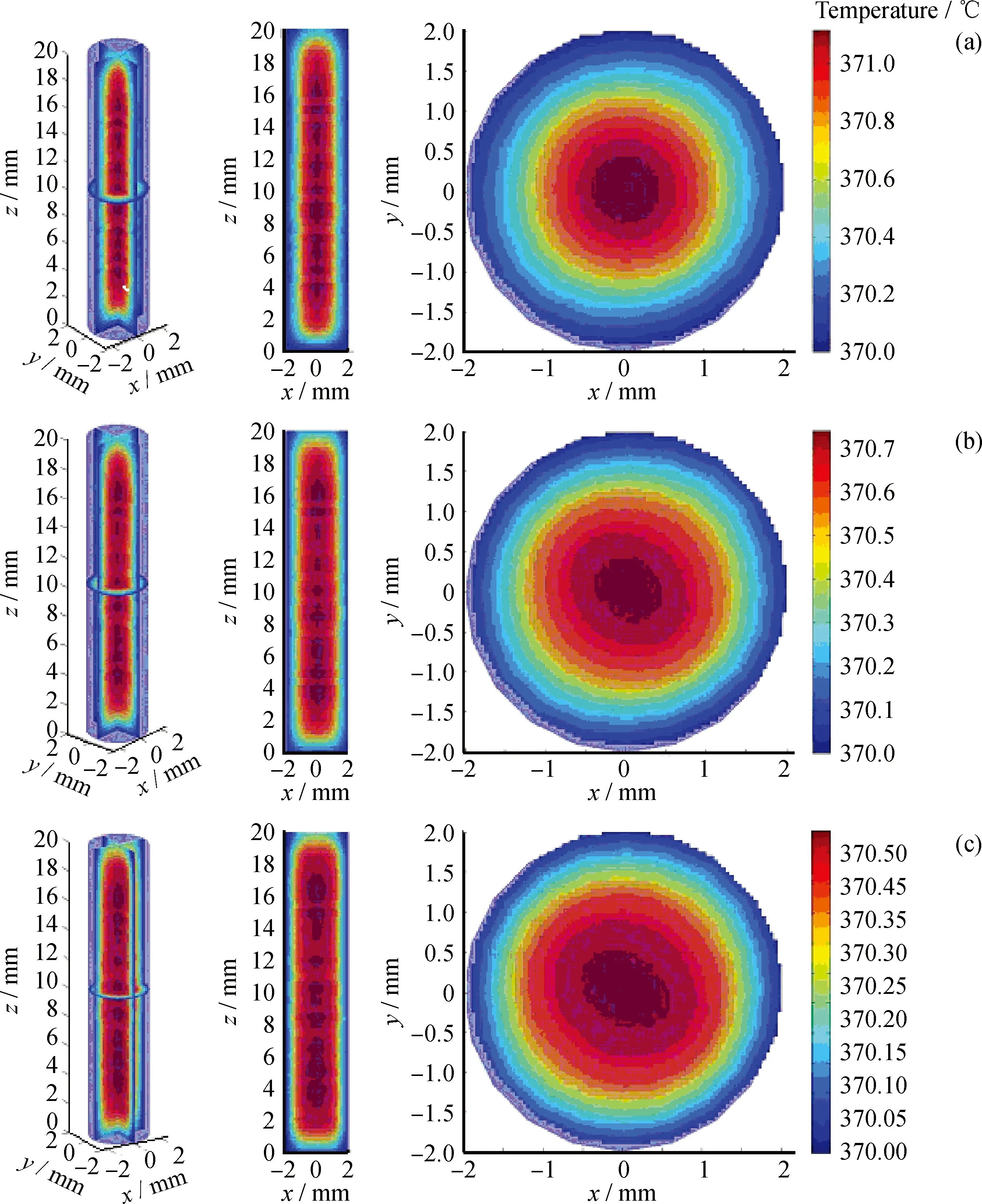
圖6 熱點蛋殼分布催化劑對應的溫度軸向及徑向分布圖Fig.6 The axial and radial temperature distributions of the catalyst with hot spot eggshell distributionSerical number: (a) 20; (b) 21; (c) 22

3 結 論

(1)即使在理想的宏觀等溫反應條件下，圓柱型催化劑顆粒內部仍然是具有非恒定溫度場分布的非等溫反應區域。

(2)在常規加氫裂化反應中，較高的反應熱、較高的處理空速、較大的原料油密度以及較大的催化劑顆粒半徑和軸向長度均導致較高的催化劑內部溫度。其中，反應熱和催化劑顆粒半徑對于催化劑內部溫度的影響更顯著。

(3)熱點蛋殼型分布的圓柱型催化劑內部溫度梯度及溫度波動相對最低，熱點均勻分布的圓柱型型催化劑次之，熱點蛋黃型分布的圓柱型催化劑的熱點更為集中。熱點分布的過度集中更容易導致催化劑的飛溫現象。

符號說明：

A——無網格計算使用的中間生成矩陣；

A1——蛋殼型催化劑功率計算的調制參數；

B——無網格計算使用的中間生成矩陣；

B1——蛋殼型催化劑功率計算的調制參數；

B2——蛋殼型催化劑功率計算的調制參數；

C——蛋黃型催化劑功率計算的調制參數；

D——蛋黃型催化劑功率計算的調制參數；

F(x,y,z)——體系內溫度對于空間的函數；

G(x，y，z)——體系的表面溫度函數；

L——無網格計算使用的三維二次基底函數集合；

LHSV ——加氫裂化反應空速， h-1；

PT——無網格計算使用的計算點局域矩陣；

Qm——加氫裂化反應熱， J/g；

Qv——單位體積催化劑單位時間放熱，kJ/(L· h)；

qv(x,y,z)——體系的熱源函數；

x，y，z——體系的空間坐標；

W——催化劑單位體積熱功率，W/mm3；

λ——催化劑顆粒導熱系數，W/(m·K)；

ρ——加氫裂化反應原料油密度， kg/L；

Φ(x,y,z)——無網格生成的形函數矩陣；

ωx(Rx)——無網格計算使用的x方向的3次樣條權重函數；

ωy(Ry)——無網格計算使用的y方向的3次樣條權重函數；

ωz(Rz)——無網格計算使用的z方向的3次樣條權重函數；

ω(x-xi,y-yi,z-zi)——無網格計算使用的3維權重樣條函數；

Ω(x,y,z)——無網格計算使用的三維權重矩陣。

[1] 尹兆林. 煉油企業全廠用能分析及節能優化[J].石油煉制與化工， 2012， 43(10): 86-91. (YIN Zhaolin. Energy consumption analysis and optimization of a refining enterprise[J].Petroleum Processing and Petrochemicals, 2012， 43(10): 86-91.)

[2] 董兆海, 袁永新, 王明傳. 加氫裂化裝置能耗及節能分析[J].齊魯石油化工, 2011, 39(2): 87-91. (DONG Zhaohai， YUAN Yongxin， WANG Mingchuan. Analysis on energy consumption and saving of hydrocracking unit[J].Qilu Petrochemical Technology, 2011, 39(2): 87-91.)

[3] 劉小波， 毛羽， 王娟， 等. 基于多孔介質加氫裂化反應器多相流數值模擬[J].石油學報(石油加工)， 2012， 20(2)： 206-267. (LIU Xiaobo， MAO Yu， WANG Juan， et al. Computational fluid dynamics of multiphase flow in hydrocracking reactor based on porous media[J].Acta Petrolei Sinica (Petroleum Processing Section), 2012， 20(2)： 206-267.)

[4] 鄭忠， 何臘梅. 紅外測溫技術及在鋼鐵生產中的應用[J].工業加熱， 2005, 34(3)： 25-29. (ZHENG Zhong， HE Lamei. Infrared temperature measurement technology and its application to steel making process[J].Industrial Heating, 2005, 34(3)： 25-29.)

[5] 王曉丹， 吳崇明. 基于MATLAB的系統分析與設計-圖像處理[M].西安： 西安電子科技大學出版社， 2000.

[6] 劉欣. 無網格方法[M].北京： 科學出版社， 2011.

[7] 劉維. 實戰Matlab之并行程序設計[M].北京： 北京航空航天大學出版社， 2012： 135-137.

[8] 龍軍, 邵潛, 賀振富, 等.規整結構催化劑及反應器研究進展[J].化工進展, 2004, 23(9): 925-931. (LONG Jun, SHAO Qian, HE Zhenfu, et al. Monolithic catalysts and monolithi rectors[J].Chemical Industry and Engineering Progess, 2004, 23(9): 925-931.)

[9] 梁文杰， 闕國和. 石油化學[M].東營： 中國石油大學出版社， 2011： 356.

[10] 吳建民， 張海濤， 應衛勇， 等. 鈷基催化劑固定床有效導熱系數[J].過程工程學報， 2010, 10(1)： 29-34. (WU Jianmin, ZHANG Haitao, YING Weiyong, et al. Effective thermal conductivity of fixed packing bed of cobalt-based catalyst[J].The Chinese Journal of Process Engineering， 2010, 10(1)： 29-34.)

[11] LIU G R， GU Y T. 無網格法理論及程序設計[M].濟南： 山東大學出版社， 2007.

[12] 莫爾比代利M， 加夫里迪斯A， 瓦爾馬A. 催化劑設計[M].北京： 化學工業出版社， 2004.

[13] 廖玉麟. 數學物理方程[M].上海： 華東理工大學出版社， 1995： 12-13.

[14] 貝新源， 岳宗五. 三維SPH程序及其在斜高速碰撞問題中的應用[J].計算物理， 1997， 14(2)： 155-166. (BEI Xinyuan, YUE Zongwu. A study on 3 dimension SPH[J]. Chinese Journal of Computation Physics, 1997， 14(2)： 155-166.)

[15] 張雄， 劉巖. 無網格方法[M].北京： 清華大學出版社， 2001.

[16] 鐘萬勰. 彈性力學求解新體系[M].大連： 大連理工大學出版社， 1995.

The Numerical Simulation About Temperature Distribution ofCylinder Catalyst by Meshless Method

WANG Kuo

(FushunResearchInstituteofPetroleumandPetrochemical,SINOPEC,Fushun113001,China)

Based on three-dimensional environment of real cylinder hydrocracking catalyst， the meshless calculation to solve Fourier partial differential equation was provided with industrial operating temperature as the boundary condition. The influence of external temperature on the internal temperature distribution of the catalyst was analyzed with the calculated results. The analysis results showed that during the actual reactions there was not isothermal inside catalyst particle. At the same time, the temperature distribution in bulk catalyst was restricted by the reaction temperature of hydrocracking process outside and internal hotspot distribution of the catalyst particle. The average temperature of bulk catalyst phase was influenced by reaction enthalpy, catalyst particle size, material oil density, reaction space velocity and catalyst inner hotspot distribution.

hydrocracking; thermal conductivity; meshless; numerical simulation; distributed computing

2016-04-20

中國石油化工股份有限公司總和課題(JQ-011308)資助 作者簡介： 王闊，男，工程師，碩士，研究方向為工業催化與分子模擬；E-mail:wangkuo.fshy@sinopec.com

1001-8719(2017)02-0310-10

TQ 116.2

A

10.3969/j.issn.1001-8719.2017.02.016